Longest common substring

The picture shows two strings where the problem has multiple solutions. Although the substring occurrences always overlap, it is impossible to obtain a longer common substring by "uniting" them.

The strings "ABABC", "BABCA" and "ABCBA" have only one longest common substring, viz. "ABC" of length 3. Other common substrings are "A", "AB", "B", "BA", "BC" and "C".

  ABABC
    |||
   BABCA
    |||
    ABCBA

Given two strings, ${\displaystyle S}$ of length ${\displaystyle m}$ and ${\displaystyle T}$ of length ${\displaystyle n}$, find a longest string which is substring of both ${\displaystyle S}$ and ${\displaystyle T}$.

A generalization is the k-common substring problem. Given the set of strings ${\displaystyle S=\{S_{1},\ldots ,S_{K}\}}$, where ${\displaystyle |S_{i}|=n_{i}}$ and ${\textstyle \sum n_{i}=N}$. Find for each ${\displaystyle 2\leq k\leq K}$, a longest string which occurs as substring of at least ${\displaystyle k}$ strings.

One can find the lengths and starting positions of the longest common substrings of ${\displaystyle S}$ and ${\displaystyle T}$ in ${\displaystyle \Theta }$${\displaystyle (n+m)}$ time with the help of a generalized suffix tree. A faster algorithm can be achieved in the word RAM model of computation if the size ${\displaystyle \sigma }$ of the input alphabet is in ${\displaystyle 2^{o\left({\sqrt {\log(n+m)}}\right)}}$. In particular, this algorithm runs in ${\textstyle O\left((n+m)\log \sigma /{\sqrt {\log(n+m)}}\right)}$ time using ${\displaystyle O\left((n+m)\log \sigma /\log(n+m)\right)}$ space.^[1] Solving the problem by dynamic programming costs ${\displaystyle \Theta (nm)}$. The solutions to the generalized problem take ${\displaystyle \Theta (n_{1}+\cdots +n_{K})}$ space and ${\displaystyle \Theta (n_{1}\cdots n_{K})}$ time with dynamic programming and take ${\displaystyle \Theta (n_{1}+\cdots +n_{K})}$ time with a generalized suffix tree.

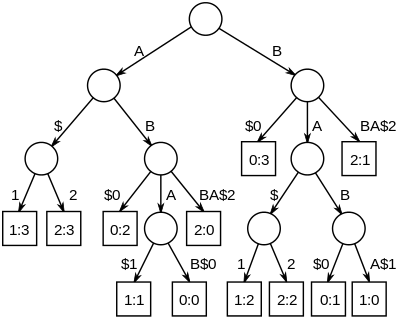
The longest common substrings of a set of strings can be found by building a generalized suffix tree for the strings, and then finding the deepest internal nodes which have leaf nodes from all the strings in the subtree below it. The figure on the right is the suffix tree for the strings "ABAB", "BABA" and "ABBA", padded with unique string terminators, to become "ABAB$0", "BABA$1" and "ABBA$2". The nodes representing "A", "B", "AB" and "BA" all have descendant leaves from all of the strings, numbered 0, 1 and 2.

Building the suffix tree takes ${\displaystyle \Theta (N)}$ time (if the size of the alphabet is constant). If the tree is traversed from the bottom up with a bit vector telling which strings are seen below each node, the k-common substring problem can be solved in ${\displaystyle \Theta (NK)}$ time. If the suffix tree is prepared for constant time lowest common ancestor retrieval, it can be solved in ${\displaystyle \Theta (N)}$ time.^[2]

The following pseudocode finds the set of longest common substrings between two strings with dynamic programming:

function LongestCommonSubstring(S[1..r], T[1..n])
    L := array(1..r, 1..n)
    z := 0  # length of the longest common substring found so far
    ret := {}

    for i := 1..r
        for j := 1..n
            if S[i] = T[j]
                if i = 1 or j = 1
                    L[i, j] := 1
                else
                    L[i, j] := L[i − 1, j − 1] + 1
                if L[i, j] > z
                    z := L[i, j]
                    ret := {S[(i − z + 1)..i]}
                else if L[i, j] = z
                    ret := ret ∪ {S[(i − z + 1)..i]}
            else
                L[i, j] := 0
    return ret

This algorithm runs in ${\displaystyle O(nr)}$ time. The array L stores the length of the longest common suffix of the prefixes S[1..i] and T[1..j] which end at position i and j, respectively. The variable z is used to hold the length of the longest common substring found so far. The set ret is used to hold the set of strings which are of length z. The set ret can be saved efficiently by just storing the index i, which is the last character of the longest common substring (of size z) instead of S[(i-z+1)..i]. Thus all the longest common substrings would be, for each i in ret, S[(ret[i]-z)..(ret[i])].

The following tricks can be used to reduce the memory usage of an implementation:

• Keep only the last and current row of the DP table to save memory (${\displaystyle O(\min(r,n))}$ instead of ${\displaystyle O(nr)}$)
  • The last and current row can be stored on the same 1D array by traversing the inner loop backwards
• Store only non-zero values in the rows. This can be done using hash-tables instead of arrays. This is useful for large alphabets.

• Longest palindromic substring
• n-gram, all the possible substrings of length n that are contained in a string