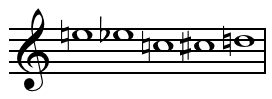Hubbry Logo
Set (music)Set (music)Main
Open search
Set (music)
Community hub
Set (music)
logo
8 pages, 0 posts
0 subscribers
Be the first to start a discussion here.
Be the first to start a discussion here.
Set (music)
Set (music)
Set (music)
View on Wikipedia
from Wikipedia
Six-element set of rhythmic values used in Variazioni canoniche by Luigi Nono[1]

A set (pitch set, pitch-class set, set class, set form, set genus, pitch collection) in music theory, as in mathematics and general parlance, is a collection of objects. In musical contexts the term is traditionally applied most often to collections of pitches or pitch-classes, but theorists have extended its use to other types of musical entities, so that one may speak of sets of durations or timbres, for example.[2]

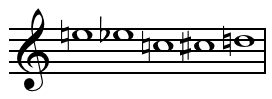
Prime form of five pitch class set from Igor Stravinsky's In memoriam Dylan Thomas[3]
Set 3-1 has three possible rotations/inversions, the normal form of which is the smallest pie or most compact form

A set by itself does not necessarily possess any additional structure, such as an ordering or permutation. Nevertheless, it is often musically important to consider sets that are equipped with an order relation (called segments); in such contexts, bare sets are often referred to as "unordered", for the sake of emphasis.[4]

Two-element sets are called dyads, three-element sets trichords (occasionally "triads", though this is easily confused with the traditional meaning of the word triad). Sets of higher cardinalities are called tetrachords (or tetrads), pentachords (or pentads), hexachords (or hexads), heptachords (heptads or, sometimes, mixing Latin and Greek roots, "septachords"),[5] octachords (octads), nonachords (nonads), decachords (decads), undecachords, and, finally, the dodecachord.

A time-point set is a duration set where the distance in time units between attack points, or time-points, is the distance in semitones between pitch classes.[6]

Serial

[edit]

In the theory of serial music, however, some authors[weasel words] (notably Milton Babbitt[7][page needed][need quotation to verify]) use the term "set" where others would use "row" or "series", namely to denote an ordered collection (such as a twelve-tone row) used to structure a work. These authors[weasel words] speak of "twelve tone sets", "time-point sets", "derived sets", etc. (See below.) This is a different usage of the term "set" from that described above (and referred to in the term "set theory").

For these authors,[weasel words] a set form (or row form) is a particular arrangement of such an ordered set: the prime form (original order), inverse (upside down), retrograde (backwards), and retrograde inverse (backwards and upside down).[2]

A derived set is one which is generated or derived from consistent operations on a subset, for example Webern's Concerto, Op.24, in which the last three subsets are derived from the first:[8]

{ \override Score.TimeSignature #'stencil = ##f \override Score.SpacingSpanner.strict-note-spacing = ##t \set Score.proportionalNotationDuration = #(ly:make-moment 1/1) \relative c'' { \time 3/1 \set Score.tempoHideNote = ##t \tempo 1 = 60 b1 bes d es, g fis aes e f c' cis a } }

This can be represented numerically as the integers 0 to 11: 

0 11 3 4 8 7 9 5 6 1 2 10

The first subset (B B♭ D) being: 

0 11 3 prime-form, interval-string = ⟨−1 +4⟩

The second subset (E♭ G F♯) being the retrograde-inverse of the first, transposed up one semitone: 

  3 11 0 retrograde, interval-string = ⟨−4 +1⟩ mod 12
  
  3  7 6 inverse, interval-string = ⟨+4 −1⟩ mod 12
+ 1  1 1
  ------
= 4  8 7

The third subset (G♯ E F) being the retrograde of the first, transposed up (or down) six semitones: 

  3 11 0 retrograde
+ 6  6 6
  ------
  9  5 6

And the fourth subset (C C♯ A) being the inverse of the first, transposed up one semitone: 

  0 11  3 prime form, interval-vector = ⟨−1 +4⟩ mod 12 

  0  1  9 inverse, interval-string = ⟨+1 −4⟩ mod 12
+ 1  1  1
  -------
  1  2 10

Each of the four trichords (3-note sets) thus displays a relationship which can be made obvious by any of the four serial row operations, and thus creates certain invariances. These invariances in serial music are analogous to the use of common-tones and common-chords in tonal music.[citation needed]

Non-serial

[edit]
Main article: Set theory (music)
Major second on C Playⓘ.
Minor seventh on C Playⓘ.
Inverted minor seventh on C (major second on B♭) Playⓘ.

The fundamental concept of a non-serial set is that it is an unordered collection of pitch classes.[9]

The normal form of a set is the most compact ordering of the pitches in a set.[10] Tomlin defines the "most compact" ordering as the one where, "the largest of the intervals between any two consecutive pitches is between the first and last pitch listed".[10] For example, the set (0,2) (a major second) is in normal form while the set (0,10) (a minor seventh, the inversion of a major second) is not, its normal form being (10,0).

Rather than the "original" (untransposed, uninverted) form of the set, the prime form may be considered either the normal form of the set or the normal form of its inversion, whichever is more tightly packed.[11] Forte (1973) and Rahn (1980) both list the prime forms of a set as the most left-packed possible version of the set. Forte packs from the left and Rahn packs from the right ("making the small numbers smaller," versus making, "the larger numbers ... smaller"[12]). For many years it was accepted that there were only five instances in which the two algorithms differ.[13] However, in 2017, music theorist Ian Ring discovered that there is a sixth set class where Forte and Rahn's algorithms arrive at different prime forms.[14] Ian Ring also established a much simpler algorithm for computing the prime form of a set,[14] which produces the same results as the more complicated algorithm previously published by John Rahn.

Vectors

[edit]
Main article: List of set classes

See also

[edit]

References

[edit]

Further reading

[edit]
[edit]
Revisions and contributorsEdit on WikipediaRead on Wikipedia

Set (music)

View on Grokipedia
from Grokipedia
In music theory, a set (or pitch-class set) is an unordered collection of distinct pitch classes—representations of pitches the , typically numbered from 0 to 11—used to analyze the structure and relationships in atonal and post-tonal , emphasizing intervallic content over traditional tonal hierarchies. This approach treats musical elements as mathematical sets, allowing for the identification of recurring patterns, symmetries, and transformations without reliance on keys or scales. Pitch-class set theory emerged in the early alongside the development of atonal by composers such as , , and , who abandoned functional in favor of free chromaticism around 1908. It was formalized as a systematic analytical method in the mid-20th century, with significant contributions from American theorists including , David Lewin, and especially Allen Forte, whose 1973 book The Structure of Atonal Music provided a comprehensive framework, including catalogs of all possible set classes up to nine pitch classes. Forte's work built on earlier ideas from European theorists but adapted from to analysis, influencing and in the 1970s and beyond. Subsequent refinements, such as John Rahn's modifications to prime forms in Basic Atonal Theory (1980), addressed inconsistencies in set representations. Central concepts in pitch-class set theory include normal order, which arranges the pitch classes of a set in ascending order within a single octave to minimize the span between the first and last note; prime form, the most compact version of a set class obtained by transposition to start at 0 and selecting the tightest ; and interval vectors (or interval-class vectors), six-digit binary strings that count the occurrences of each interval class (from minor second to ) within a set, facilitating comparisons of intervallic similarity. Basic operations on sets encompass transposition (shifting all pitch classes by a fixed interval modulo 12), inversion (reflecting intervals around a central pitch class), union (combining sets), (shared elements), and complement (pitch classes absent from the set), enabling the exploration of inclusions, subsets, and transformations. These tools reveal structural coherence in otherwise dissonant or fragmented music. The theory is primarily applied to 20th-century expressionist and serialist compositions, such as Schoenberg's (1912) or Webern's Five Movements for String Quartet, Op. 5 (1909), where sets highlight motivic invariance and aggregate formations under twelve-tone techniques. It has also extended to , , and computer-assisted composition, though critics note its limitations in addressing , , or perceptual aspects of sound. Despite these, set theory remains a foundational method in undergraduate music curricula for understanding post-tonal structures.

Basic Concepts

Pitch Sets and Pitch-Class Sets

In musical set theory, a pitch set is defined as an unordered collection of specific pitches, each identified by its distinct frequency and register, without regard to sequence or hierarchy. For example, the major triad consisting of the pitches C4, E4, and G4 forms the pitch set {C4, E4, G4}, which emphasizes the simultaneous presence of these exact tones rather than their melodic or harmonic function in traditional tonality. Pitch-class sets extend this concept by abstracting away from specific registers, treating pitches as equivalence classes modulo 12 semitones to account for octave equivalence, and further considering transpositional invariance. This means that any transposition of a collection of pitches, or its octave displacement, belongs to the same pitch-class set; for instance, {C4, E4, G4}, {D4, F♯4, A4}, and {C5, E5, G5} all represent the same pitch-class set. To facilitate analysis, pitch classes are denoted by integers from 0 to 11, where C (or B♯) is 0, C♯/D♭ is 1, D is 2, and so on up to B as 11, operating within a 12-tone universe that encompasses the chromatic scale. The conversion from a pitch set to a pitch-class set involves mapping each pitch to its corresponding pitch-class integer and then normalizing the collection to a canonical form, such as starting from 0 for the lowest element after transposition. Thus, the pitch set {C4, E4, G4} converts to the pitch-class set {0, 4, 7}, where the intervals are measured in semitones (4 from 0 to 4, 7 from 0 to 7). This notation highlights the set's intervallic structure independent of absolute pitch height. Within the 12-tone universe, basic set operations on pitch-class sets include union, which combines all unique elements from two or more sets (e.g., {0, 4} ∪ {4, 7} = {0, 4, 7}); , which retains only the shared elements (e.g., {0, 4, 7} ∩ {4, 7, 11} = {4, 7}); and complement, which yields the pitch classes absent from the set (e.g., the complement of {0, 4, 7} is {1, 2, 3, 5, 6, 8, 9, 10, 11}). These operations treat sets as unordered, distinguishing them from ordered structures such as scales or twelve-tone rows, where sequence and directionality play a defining role.

Normal Order and Prime Form

In pitch-class set theory, the normal order of a set is defined as the ascending sequence of its pitch classes arranged to produce the most compact linear representation within a single octave, facilitating direct comparison between sets. This form minimizes the overall span by selecting the rotation that follows the largest gap in the circular arrangement of pitch classes on the modulo-12 clock face. For instance, the pitch-class set {0,4,7}, corresponding to a major triad, is already in normal order as [0,4,7] since it spans only 7 semitones with no larger internal gap. The algorithm for determining normal order proceeds as follows: first, list the distinct in ascending order from 0 to 11; second, append a duplicate of the first pitch class to the end of the list to simulate circularity; third, calculate the intervals between consecutive elements and identify the largest such interval (the principal gap); fourth, the sequence to begin immediately after this gap, yielding the . If ties occur in the gap size, select the rotation that results in the smallest subsequent intervals when compared lexicographically. The prime form extends this concept to account for transposition and inversion equivalence, representing the most compact version of the normal order across all possible transpositions of the set and its inversion, always starting from pitch class 0. It is obtained by selecting, between the transposed normal order (P-form) and the transposed normal order of the inversion (I-form), the one with the smallest initial interval from 0; if tied, compare the next interval, continuing until a difference emerges. This standardization, introduced by Allen Forte, ensures a unique identifier for each set class, independent of register or orientation. To derive the prime form step by step: begin with the pitch-class set and compute its ; transpose this so the first element is to obtain the P-form; next, invert the original set by mapping each pitch class pcpc to [0](/page/0)[0](/page/0) if pc=[0](/page/0)pc = [0](/page/0), or 12−pc12 - pc otherwise, then find the of this inverted set and it to start at for the I-form; finally, compare the P-form and I-form sequences position by position, selecting the lexicographically smaller one as the prime form. For the diminished triad {0,3,6}, the is [0,3,6], yielding P-form [0,3,6]; its inversion is also {0,3,6} (self-inverting), so the I-form is identical, and the prime form is [0,3,6]. As an example of derivation for a larger set, consider the diatonic collection {0,2,4,5,7,9,11}, with normal order [0,2,4,5,7,9,11] spanning 11 semitones. Transposing to start at 0 gives the P-form [0,2,4,5,7,9,11]. The inversion maps to {0,1,3,5,7,8,10} (subtracting each from 12 12), whose normal order is [0,1,3,5,7,8,10], giving the I-form [0,1,3,5,7,8,10]. Comparing [0,2,4,5,7,9,11] and [0,1,3,5,7,8,10], the second element differs (2 vs. 1), so the prime form is [0,1,3,5,7,8,10], reflecting the more compact inverted orientation.

Interval Relations

Interval Content

In pitch-class set theory, interval content refers to the multiset of all unordered pairwise intervals between the pitch classes in a set, where each interval is measured in semitones and reduced to its interval class (ic), ranging from 1 to 6 semitones—the smallest distance around the . Interval classes represent equivalence classes of intervals under inversion: ic1 denotes the (or ), ic2 the (or ), ic3 the (or ), ic4 the (or ), ic5 the (or ), and ic6 the . This concept captures the relational properties of a set without regard to order or octave position, focusing solely on the unordered interval classes derived from the minimal distances modulo 12. To calculate the interval content of a set with cardinality nn, determine the (n2)\binom{n}{2} unique unordered pairs of pitch classes, compute the semitone distance for each (the minimum of ∣pi−pj∣|p_i - p_j| and 12−∣pi−pj∣12 - |p_i - p_j|), and collect these as interval classes with their multiplicities. For example, the set {0,1,6} yields pairs (0,1) with distance 1 (ic1), (1,6) with distance 5 (ic5), and (0,6) with distance 6 (ic6), resulting in the multiset {ic1, ic5, ic6}, each with multiplicity one. Similarly, the major triad {0,4,7} produces pairs (0,4) with ic4, (4,7) with ic3, and (0,7) with ic5, giving {ic3, ic4, ic5}, each appearing once. These calculations are typically performed on a set in prime form to ensure consistency across transpositions and inversions. Interval content plays a key role in assessing harmonic relatedness between sets, as shared or overlapping multisets of interval classes indicate sonic similarity independent of specific pitch content or formal vector encoding. For instance, sets with identical interval content, such as Z-related hexachords, exhibit the same overall intervallic structure despite belonging to distinct set classes, highlighting structural affinities in atonal . This relational measure provides a foundational tool for analyzing consonance, dissonance, and progression without invoking higher-level abstractions.

Interval Vectors

In musical set theory, the interval vector provides a formal encoding of a pitch-class set's interval content as a six-element ⟨a1,a2,a3,a4,a5,a6⟩\langle a_1, a_2, a_3, a_4, a_5, a_6 \rangle, where each aia_i represents the number of occurrences of interval class ii (with i=1i=1 denoting a minor second or , up to i=6i=6 for a ) among all unordered pairs of pitch classes in the set. This vector, introduced by Allen Forte, captures the of unordered interval classes while disregarding order and registration, offering a compact summary of the set's intervallic structure. To compute the interval vector, first represent the pitch-class set in normal order (ascending integers from 0 to 11, starting at the lowest pitch class). Then, calculate the interval class for every unordered pair of pitch classes by taking the minimum of the absolute difference dd and 12−d12 - d modulo 12, and tally the frequency of each resulting interval class from 1 to 6. For instance, the major triad with pitch classes {0,4,7}\{0,4,7\} yields pairwise interval classes of pairs (0,4) with ic4, (4,7) with ic3, and (0,7) with ic5 (since min(7,5)=5), resulting in one each of ic3, ic4, and ic5, for the vector ⟨0,0,1,1,1,0⟩\langle 0,0,1,1,1,0 \rangle. Interval vectors exhibit key properties that facilitate comparative analysis: they remain invariant under transposition (addition of a constant 12) and inversion (reflection around a , equivalent to subtraction from 12), preserving the set's essential sonic profile across transformations. A notable exception arises in Z-relations, where two distinct set classes share the same interval vector but cannot be derived from one another via transposition or inversion; for example, the hexachords {0,1,2,5,6,8}\{0,1,2,5,6,8\} (Forte 6-Z43) and {0,1,3,6,8,9}\{0,1,3,6,8,9\} (Forte 6-Z49) both have the vector ⟨3,2,2,3,3,2⟩\langle 3,2,2,3,3,2 \rangle, highlighting structural ambiguities in larger sets. Representative examples illustrate these vectors' utility. The whole-tone hexachord {0,2,4,6,8,10}\{0,2,4,6,8,10\} (Forte 6-35) produces ⟨0,6,0,6,0,3⟩\langle 0,6,0,6,0,3 \rangle, reflecting six minor seconds/major sevenths, six major seconds/minor sevenths, and three s among its 15 pairs, emphasizing its even-stepped, ambiguous character. In contrast, a like {0,3,6}\{0,3,6\} yields ⟨0,0,2,0,0,1⟩\langle 0,0,2,0,0,1 \rangle, with two minor thirds and one . Beyond summarization, interval vectors enable quantitative assessment of set relationships, particularly in inclusion arrays, where the vector of a potential is compared component-wise to that of a larger set to determine embeddability (e.g., verifying if a triad's vector aligns within a surrounding hexachord's counts without exceeding them). This method, rooted in Forte's framework, supports systematic identification of while prioritizing the conceptual role of intervals over exhaustive enumeration.

Analytical Applications

Serial Contexts

In 12-tone serial music, pitch-class sets integrate with the compositional framework by treating the tone row—an ordered arrangement of all 12 pitch classes, known as the aggregate—as a source for deriving unordered subsets that reveal structural invariances across transformations. Analysts apply set classes to examine how portions of the row, such as hexachords or tetrachords, recur in equivalent forms despite the row's linear progression, thereby highlighting harmonic consistency in works by composers like . The aggregate forms through the partitioning of row forms—prime (P), retrograde (R), inversion (I), and retrograde-inversion (RI)—into invariant subsets that maintain their pitch-class content under these operations. In particular, (six-note subsets) are often analyzed using prime forms to identify combinatorial properties, where the first hexachord of one row form complements or matches the second hexachord of another, ensuring aggregate completion without repetition. This approach allows for the detection of recurring set classes in derived row segments, facilitating a deeper understanding of serial derivation. A prominent example appears in Alban Berg's Lyric Suite (1925–1926), where the primary row's hexachords belong to set classes 6-Z44 and its complement 6-Z19, enabling invariant formations across P, I, and other transformations that preserve the aggregate while embedding personal tonal allusions, such as Berg's name in note letters. These Z-related hexachords (sharing the same interval vector) underscore Berg's hybrid serial style, blending strict row adherence with expressive subset recurrences. Set-theoretic operations like retrograde and inversion preserve the interval vectors of row subsets, as these transformations maintain the multiset of interval classes within the pitch-class , allowing analysts to compare profiles across row forms without altering their intervallic essence. Despite these insights, pitch-class set has limitations in serial contexts, as sets are inherently unordered collections that overlook the row's specific linear ordering and rhythmic placement, which are essential to the temporal and motivic dimensions of 12-tone composition.

Non-Serial Contexts

In non-serial atonal music, pitch-class facilitates the of free harmonic combinations and motivic structures by treating unordered collections of pitch classes as set classes, independent of serial row derivations. Fortean , named after Allen Forte, segments musical surfaces into these sets—ranging from dyads to undecachords, labeled 2-1 through 11-1—and examines their prime forms and interval content to uncover recurring patterns and relationships. For instance, the , with prime form [0,4,8], is classified as 3-12, a symmetrical trichord that appears frequently in atonal textures due to its enharmonic equivalences across transpositions. This approach emphasizes the aggregate's subsets rather than linear ordering, allowing analysts to trace harmonic coherence in works like those of early 20th-century modernists. Subset and superset relations form a core analytical tool, using inclusion tables to map how smaller sets embed within larger ones, revealing hierarchical organizations within the chromatic aggregate (set class 12-1). Forte's comprehensive tables detail these embeddings via inclusion vectors, where each entry indicates the number of transposed or inverted subsets of a given contained in a set class; for example, major triads (3-11, prime form [0,4,7]) appear in 12 distinct transpositions within the aggregate, illustrating exhaustive coverage through overlap. Such relations highlight motivic proliferation: a like 4-19 ([0,1,4,7]) might contain multiple 3-11 subsets, enabling the derivation of larger harmonies from basic cells. These embeddings provide quantitative insight into structural depth without relying on tonal functions. Analytical applications in non-serial contexts often focus on specific composers' pre-serial output. In Igor Stravinsky's Piano Rag-Music (1919), an atonal work blending and , tetrachords from set class 4-20 ([0,1,5,8]) recur prominently, forming pentachordal and hexachordal supersets that unify sections through shared interval vectors (0,1,1,2,2,0). This all-interval tetrachord, containing diverse trichords like 3-1 and 3-5, underscores Stravinsky's mosaic-like construction, where fragmented sets aggregate into larger wholes. Similarly, Anton Webern's Six Bagatelles for , Op. 9 (1913), employs the octatonic collection (8-28, [0,1,3,4,6,7,9,10]) as a superset framework, from which subsets such as 4-22 ([0,2,4,7]) derive aphoristic motives, emphasizing sparse textures and inversional symmetry. These examples demonstrate how set classes illuminate invariance amid apparent fragmentation. Beyond interval vectors, which quantify internal interval-class distributions, similarity relations assess equivalence between distinct set classes via shared maximal subsets. Forte's K-relations, applicable to hexachords, identify pairs that share identical tetrachordal or trichordal content under transposition and inversion; for instance, 6-7 ([0,1,2,6,7,8]) and 6-20 ([0,1,4,5,6,8]) are K-related, each containing the same four trichords (e.g., 3-1, 3-2), facilitating analysis of near-identical harmonic fields in non-serial music. These relations extend to R_p and R_1 metrics for adjacent sets differing by one , promoting comparisons of "near-equivalent" collections that approximate tonal substitutions. Such tools reveal subtle affinities, enhancing interpretations of harmonic progression in free atonal writing. Although set theory originated with pitch organization, extensions to rhythm and timbre via generalized interval systems have been proposed, treating these parameters as spaces for analogous set relations. David Lewin's framework in Generalized Musical Intervals and Transformations (1987) models rhythmic durations or timbral qualities as GIS objects, where intervals function transformationally across domains; however, practical applications in non-serial analysis remain centered on pitch sets, with rhythmic or timbral generalizations appearing sporadically in advanced studies.

Historical Development

Origins in Atonal Theory

The emergence of set theory in music can be traced to the early 20th century, amid the breakdown of traditional tonality in Western art music, as composers sought new ways to organize pitch relations without a tonal center. This period marked a shift from functional harmony to more abstract pitch configurations, with initial conceptual foundations laid in Arnold Schoenberg's writings on the "suspension of the laws of tonal harmony." In his Theory of Harmony (1911), Schoenberg described how dissonance had expanded to the point where tonal functions were suspended, allowing for freer combinations of pitches that prefigured the unordered collections later formalized as sets. Schoenberg's essays from the 1910s, such as those in Der blaue Reiter almanac (1912), further emphasized the emancipation of dissonance and the need for motivic coherence in atonal contexts, responding to the expressive demands of expressionism. The rise of the 12-tone technique in the 1920s, pioneered by Schoenberg and , implicitly relied on set aggregates, as the encompassed all 12 pitch classes without tonal hierarchy, creating a complete chromatic set from which subsets derived motivic material. Independently, Josef Matthias Hauer formulated his "law of the twelve tones" around 1920, using fixed hexachordal "tropes" as unordered pitch sets to organize atonal compositions, providing an early precursor to systematic . Schoenberg's compositions from this era, such as the Five Piano Pieces, Op. 23 (1923), used row forms that aggregated pitches in ways later analyzed set-theoretically, though contemporaries viewed them through serial rather than combinatorial lenses. Webern's rows similarly treated the aggregate as a unified entity, but systematic set analysis did not emerge until the post-World War II period. A key early text hinting at set relations without formal notation was René Leibowitz's Introduction to Twelve-Tone Music (1947), which explored combinatorial properties of rows and their subsets, emphasizing invariant pitch collections across transformations. Leibowitz discussed how row segments formed recurring pitch groups that maintained structural unity, bridging intuitive serial practice with proto-set-theoretic insights, though he stopped short of developing notation for prime forms or interval vectors. The transition to formal revealed significant gaps in pre-1950s atonal analysis, where composers and theorists depended on intuition and descriptions rather than systematic tools for comparing pitch collections. While Schoenberg and his intuitively manipulated set-like aggregates, the lack of rigorous limited broader application, setting the stage for systematization. Pitch-class sets evolved from these early atonal pitch collections, providing a retrospective framework for understanding pre-serial works.

Key Contributors and Evolution

played a pivotal role in the early formalization of within serial music during the 1950s, particularly through his exploration of set complexes and all-interval series, which emphasized combinatorial properties to ensure aggregate formations under transposition and inversion operations. His 1961 essay "Set Structure as a Compositional Determinant" laid foundational concepts for deriving musical structures from pitch sets, influencing subsequent analytical frameworks by highlighting contextual invariance in twelve-tone compositions. Babbitt's work introduced the idea of combinatoriality, where row segments combine to form complete pitch aggregates, extending serial techniques beyond linear ordering to multidimensional relations. Allen Forte advanced significantly in the and , culminating in his seminal 1973 book The Structure of Atonal Music, which systematized pitch-class set analysis through concepts like , prime form, and interval vectors. Forte's catalog enumerated 352 distinct set classes for cardinalities from three to nine notes, providing a comprehensive that enabled precise identification of recurring structures in atonal works independent of or register. This framework shifted focus from individual pitches to relational properties, with interval vectors serving as a key innovation for quantifying ic-content across sets. Subsequent expansions in the 1980s built on these foundations, as seen in John Rahn's Basic Atonal Theory (1980), which refined measures of set similarity through inclusion relations and rotational adjustments to Forte's prime form algorithm. David Lewin's transformational approach, detailed in Generalized Musical Intervals and Transformations (1987), integrated pitch-class sets with voice-leading transformations, modeling musical space as a network of generative operations rather than static collections. Lewin's GIS framework allowed for contextual analyses that bridged set-theoretic invariance with dynamic progressions, influencing applications in both atonal and tonal domains. The evolution of set theory extended beyond pitch to generalized domains in the 1980s, with Robert Morris applying analogous principles to rhythmic structures through beat-class sets and time-point systems, enabling serial control over duration and metric hierarchies. By the 1990s, computational tools facilitated broader adoption, such as software for generating and analyzing pitch-class sets, which automated cataloging and similarity computations to support empirical research. Criticisms of set theory highlight its limitations in capturing voice-leading parsimony or contextual functionality in tonal music, prompting alternatives like , which prioritizes smooth transformations among triads over abstract set relations.

References

  1. https://musictheory.pugetsound.edu/mt21c/SetTheorySection.html
  2. https://academicworks.cuny.edu/cgi/viewcontent.cgi?params=/context/gc_pubs/article/1473/&path_info=JStraus1991_Primer_Atonal_Set_Theory.pdf
  3. https://www.academia.edu/Documents/in/Musical_Set-theory
  4. https://pressbooks.uiowa.edu/twentieth-and-twenty-first-century-music/chapter/pitch-class/
  5. https://myweb.fsu.edu/mbuchler/Buchler_Schuijer_review.pdf
  6. https://digitalcollections.lipscomb.edu/cgi/viewcontent.cgi?article=1307&context=jmtp
  7. https://pressbooks.uiowa.edu/twentieth-and-twenty-first-century-music/chapter/pitch-class-set/
  8. https://www.clarkross.ca/460_Set_Theory_Intro.pdf
  9. https://yale.universitypress.edu/book/9780300014104/the-structure-of-atonal-music
  10. https://viva.pressbooks.pub/openmusictheory/chapter/pc-sets-normal-order-and-transformations/
  11. https://mtosmt.org/issues/mto.04.10.3/mto.04.10.3.collins.php
  12. https://musictheory.pugetsound.edu/mt21c/PrimeForm.html
  13. https://www.stephenandrewtaylor.net/music408e/IntroToSetTheory.pdf
  14. https://digitalcommons.du.edu/cgi/viewcontent.cgi?article=1003&context=gfamonographs
  15. https://sections.maa.org/mddcva/MeetingFiles/Spring2014Meeting/TalkSlides/Izmirli.pdf
  16. http://sections.maa.org/mddcva/MeetingFiles/Spring2014Meeting/TalkSlides/Izmirli.pdf
  17. https://musictheory.pugetsound.edu/mt21c/IntervalVector.html
  18. https://musictheory.pugetsound.edu/mt21c/ListsOfSetClasses.html
  19. https://hal.science/hal-00664776v1/document
  20. https://www.clarkross.ca/480_12_Tone_Technique.pdf
  21. https://viva.pressbooks.pub/openmusictheory/chapter/row-properties/
  22. https://www.jstor.org/stable/745939
  23. https://robertkelleyphd.com/home/teaching/music-theory/intro-to-post-tonal-music-analysis/
  24. https://music.utk.edu/wp-content/uploads/2023/05/NonserialAtonality.pdf
  25. https://symposium.music.org/31/item/2079-a-primer-for-atonal-set-theory.html
  26. https://www.jstor.org/stable/746011
  27. https://www.jstor.org/stable/746032
  28. https://global.oup.com/academic/product/generalized-musical-intervals-and-transformations-9780199759941
  29. https://muse.jhu.edu/book/30483/
  30. https://www.cambridge.org/core/books/cambridge-companion-to-serialism/milton-babbitt-and-total-serialism/137764AF8653CFAFD96960B074152562
  31. https://music.arts.uci.edu/abauer/4.3/readings/Pitch-Class_Set_Theory_Analyzing_Atonal_Music__Michiel_Schuijer
  32. https://www.andrew.cmu.edu/user/johnito/music_theory/20thC/LectureNotes/1-SetClasses.pdf
  33. https://academicworks.cuny.edu/context/gc_pubs/article/1473/viewcontent/JStraus1991_Primer_Atonal_Set_Theory.pdf
  34. https://dmitri.mycpanel.princeton.edu/files/publications/lewin.pdf
  35. https://www-personal.umd.umich.edu/~tmfiore/1/MAAMiniCourseOverviewSlides.pdf
  36. https://ecmc.rochester.edu/rdm/pdflib/talapaper.pdf
  37. https://mta.ca/pc-set/calculator/pc_calculate.html
  38. https://music.arts.uci.edu/abauer/3.1/notes/Cohn_Intro_nRT.pdf
Add your contribution
Related Hubs
User Avatar
No comments yet.