Set theory

Set theory is the branch of mathematics concerned with the study of sets, which are well-determined collections of distinct objects called elements or members, and it forms the foundational framework for virtually all modern mathematical disciplines by defining concepts such as numbers, functions, and relations in terms of sets and the membership relation.^[1] Developed primarily by Georg Cantor in the late 19th century, set theory revolutionized mathematics by treating infinite collections as legitimate objects comparable to finite ones, introducing notions like cardinality to measure the "size" of sets and transfinite numbers to extend the natural numbers beyond the finite.^[2] Cantor's work, beginning with his 1874 paper on the non-denumerability of the real numbers, established key results such as the uncountability of the continuum and the hierarchy of infinities, laying the groundwork for set theory as an autonomous field.^[3] Early naive set theory, which relied on intuitive notions of sets without formal restrictions, encountered paradoxes like Russell's paradox in 1901, which demonstrated that unrestricted comprehension—allowing any property to define a set—leads to contradictions, such as the set of all sets that do not contain themselves.^[1] To resolve these issues, axiomatic set theory emerged in the early 20th century, with Ernst Zermelo's 1908 axiomatization providing the first rigorous system, later refined by Abraham Fraenkel into the Zermelo-Fraenkel (ZF) axioms, which include principles like extensionality (sets are determined by their elements), pairing, union, power set, infinity, and replacement, along with the axiom schema of separation to safely form subsets.^[4] The addition of the axiom of choice (AC), which asserts the existence of choice functions for any collection of nonempty sets, completes the standard system known as ZFC, widely accepted as the basis for mathematics due to its consistency with classical theorems and ability to derive all known mathematical structures.^[4] 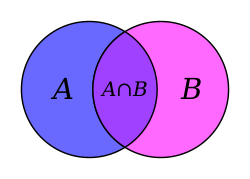Beyond its foundational role, set theory explores profound questions about the structure of the mathematical universe, including the continuum hypothesis (CH)—Cantor's conjecture that there is no set with cardinality strictly between that of the natural numbers and the real numbers—which was shown by Kurt Gödel in 1940 to be consistent with ZFC and by Paul Cohen in 1963 to be independent of it using forcing techniques.^[4] Key operations on sets, such as union, intersection, and complement, enable the construction of complex structures like ordered pairs via the Kuratowski definition $(a, b) = \{\{a\}, \{a, b\}\}$(a,b)={{a},{a,b}}, while concepts like ordinals and cardinals provide tools for ordering and sizing infinite sets.^[5] Today, set theory not only underpins pure mathematics but also influences computer science through models of computation and database theory, and philosophy via debates on the nature of infinity and mathematical existence.^[5]

Basic Concepts

Sets and Elements

In set theory, a set is defined as a well-determined collection of distinct objects, known as elements or members, where the order of elements does not matter and repetitions are not permitted. For example, the finite set {1, 2, 3} consists of the elements 1, 2, and 3, while the infinite set of natural numbers, denoted $\mathbb{N} = \{0, 1, 2, 3, \dots\}$N={0,1,2,3,…}, contains all non-negative integers without end. This foundational concept allows sets to encompass any type of objects, from numbers to more abstract entities, provided they are unambiguously specified by their membership.^[6] Membership in a set is denoted by the symbol $\in$∈, where $x \in A$x∈A indicates that $x$x is an element of set $A$A. Basic properties of membership include the fact that a set contains exactly its specified elements, with reflexivity holding such that $x \in \{x\}$x∈{x} for any $x$x, and irreflexivity for distinct elements where, if $x \neq y$x=y, then $y \notin \{x\}$y∈/{x}. A key principle is extensionality, which states that two sets are equal if and only if they have precisely the same elements: $A = B$A=B if and only if for all $x$x, $x \in A$x∈A if and only if $x \in B$x∈B. This ensures that sets are uniquely identified by their contents alone.^[6] The empty set, denoted $\emptyset$∅, is the unique set containing no elements at all, serving as a foundational building block in set theory. Singleton sets, such as $\{x\}${x}, contain exactly one element $x$x. A subset relation $A \subseteq B$A⊆B holds if every element of $A$A is also an element of $B$B, formally $\forall x (x \in A \to x \in B)$∀x(x∈A→x∈B); a proper subset $A \subset B$A⊂B requires $A \subseteq B$A⊆B and $A \neq B$A=B. The power set $\mathcal{P}(A)$P(A) of a set $A$A is the set comprising all possible subsets of $A$A, including $\emptyset$∅ and $A$A itself. For a finite set $A$A with cardinality $|A| = n$∣A∣=n, the cardinality of the power set is $|\mathcal{P}(A)| = 2^n$∣P(A)∣=2n, reflecting the $2^n$2n possible combinations of including or excluding each element.^[6] Cantor's diagonal argument provides motivation for the existence of uncountable sets by demonstrating that the power set of the natural numbers, $\mathcal{P}(\mathbb{N})$P(N), cannot be placed in one-to-one correspondence with $\mathbb{N}$N itself, implying its cardinality exceeds that of any countable infinity. This highlights how even simple constructions like power sets can generate infinities of vastly different sizes.^[7]

Set Operations and Relations

Set operations provide fundamental ways to construct new sets from existing ones, building upon the basic notion of sets and their elements. The union of two sets $A$A and $B$B, denoted $A \cup B$A∪B, is the set consisting of all elements that belong to $A$A or to $B$B (or to both); formally, $A \cup B = \{ x \mid x \in A \lor x \in B \}$A∪B={x∣x∈A∨x∈B}.^[8] This operation is commutative ($A \cup B = B \cup A$A∪B=B∪A) and associative ($(A \cup B) \cup C = A \cup (B \cup C)$(A∪B)∪C=A∪(B∪C)), allowing for unions of multiple sets.^[8] The intersection of $A$A and $B$B, denoted $A \cap B$A∩B, contains all elements common to both; formally, $A \cap B = \{ x \mid x \in A \land x \in B \}$A∩B={x∣x∈A∧x∈B}.^[8] Intersection is also commutative and associative, and it distributes over union: $A \cap (B \cup C) = (A \cap B) \cup (A \cap C)$A∩(B∪C)=(A∩B)∪(A∩C).^[8] These operations enable the formation of more complex structures while preserving the extensional equality of sets. The set difference, or relative complement, between $A$A and $B$B, denoted $A \setminus B$A∖B or $A - B$A−B, includes elements in $A$A but not in $B$B; formally, $A \setminus B = \{ x \mid x \in A \land x \notin B \}$A∖B={x∣x∈A∧x∈/B}.^[8] This can be expressed using intersection and complement: $A \setminus B = A \cap B^c$A∖B=A∩Bc, where $B^c$Bc is the complement of $B$B relative to some universal set $U$U, defined as $B^c = \{ x \in U \mid x \notin B \}$Bc={x∈U∣x∈/B}.^[8] The complement operation highlights elements outside a set within a fixed universe, though in pure set theory without a specified universe, complements are often treated relatively.^[8] For example, if $U = \{1, 2, 3, 4\}$U={1,2,3,4} and $B = \{1, 3\}$B={1,3}, then $B^c = \{2, 4\}$Bc={2,4}. These operations, including their idempotence ($A \cup A = A$A∪A=A, $A \cap A = A$A∩A=A), form the basis for Boolean algebra on sets.^[8] To construct sets of pairs, the Cartesian product of sets $A$A and $B$B, denoted $A \times B$A×B, is the set of all ordered pairs $(a, b)$(a,b) where $a \in A$a∈A and $b \in B$b∈B; formally, $A \times B = \{ (a, b) \mid a \in A, b \in B \}$A×B={(a,b)∣a∈A,b∈B}.^[8] Ordered pairs distinguish order and repetition, so $(a, b) \neq (b, a)$(a,b)=(b,a) unless $a = b$a=b. In set theory, ordered pairs are defined without primitives using the Kuratowski construction: $(a, b) = \{ \{a\}, \{a, b\} \}$(a,b)={{a},{a,b}}.^[8] This ensures $(a, b) = (c, d)$(a,b)=(c,d) if and only if $a = c$a=c and $b = d$b=d, as the singleton $\{a\}${a} uniquely identifies the first component, and the pair $\{a, b\}${a,b} the second. For instance, $(1, 2) = \{ \{1\}, \{1, 2\} \}$(1,2)={{1},{1,2}}. This definition, introduced by Kazimierz Kuratowski in 1921, allows ordered pairs to be pure sets, foundational for relations and functions.^[8] Binary relations generalize associations between elements. A binary relation $R$R from set $A$A to set $B$B is a subset of the Cartesian product $A \times B$A×B; if $B = A$B=A, it is a relation on $A$A.^[8] For $(x, y) \in R$(x,y)∈R, one writes $x R y$xRy. Key properties include reflexivity: $\forall x \in A, x R x$∀x∈A,xRx; symmetry: $\forall x, y \in A, x R y \implies y R x$∀x,y∈A,xRy⟹yRx; and transitivity: $\forall x, y, z \in A, (x R y \land y R z) \implies x R z$∀x,y,z∈A,(xRy∧yRz)⟹xRz.^[8] These properties classify relations; for example, the equality relation $=$= on a set is reflexive, symmetric, and transitive. Unrestricted comprehension in forming relations, however, leads to paradoxes like Russell's, which motivated axiomatic restrictions (detailed in the history section).^[8] An equivalence relation on a set $A$A is a binary relation that is reflexive, symmetric, and transitive, partitioning $A$A into disjoint equivalence classes $_R = \{ y \in A \mid y R x \}$R​={y∈A∣yRx}.^[8] For instance, congruence modulo $n$n on integers defines classes like even and odd numbers. A partial order is a relation that is reflexive, antisymmetric ($\forall x, y, x R y \land y R x \implies x = y$∀x,y,xRy∧yRx⟹x=y), and transitive, modeling hierarchical structures such as the subset relation $\subseteq$⊆ on sets, where $A \subseteq B$A⊆B if $A \cap B = A$A∩B=A.^[8] Partial orders may not compare all elements, unlike total orders. Functions emerge as special binary relations. A function $f: A \to B$f:A→B is a relation such that for every $a \in A$a∈A, there exists exactly one $b \in B$b∈B with $(a, b) \in f$(a,b)∈f; this $b$b is denoted $f(a)$f(a).^[8] The domain is $A$A, and the image is $\{ f(a) \mid a \in A \}${f(a)∣a∈A}. Injective functions satisfy $f(a_1) = f(a_2) \implies a_1 = a_2$f(a1​)=f(a2​)⟹a1​=a2​, surjective ones have image $B$B, and bijective ones are both. This relational view unifies functions with sets, enabling their use in constructing advanced structures like mappings between sets.^[8]

Common Notations and Conventions

In set theory, precise notation is essential for unambiguous expression of concepts, with symbols standardized over time to facilitate communication among mathematicians. The membership relation, denoting that an element belongs to a set, is represented by the symbol $\in$∈, introduced by Giuseppe Peano in 1889 as an abbreviation for the Latin "est" (meaning "is"), initially in a lunate form of epsilon.^[9] This notation largely replaced earlier verbal descriptions and alternative symbols, such as Georg Cantor's horizontal line with a vertical bar (|---), becoming widely adopted in the early 20th century through works like those of Ernst Zermelo and Abraham Fraenkel.^[9] The negation of membership, indicating an element does not belong to a set, is denoted by $\notin$∈/, a convention that emerged alongside $\in$∈ in foundational texts around the same period.^[9] Subset relations use $\subseteq$⊆ to indicate that every element of one set is also an element of another (inclusive subset), a symbol introduced by Ernst Schröder in 1890; the proper subset, where the inclusion is strict (one set is contained in but not equal to the other), is often denoted by $\subset$⊂, though usage varies and some traditions reserve $\subset$⊂ exclusively for proper subsets while employing $\subseteq$⊆ for the inclusive case.^[9] Union of sets, combining all distinct elements from two or more sets, is symbolized by $\cup$∪, and intersection, consisting of elements common to all sets, by $\cap$∩; both were introduced by Peano in 1888 in his geometric calculus.^[9] The Cartesian product of two sets, forming ordered pairs from their elements, is denoted by $\times$×, a notation established in the early 20th century alongside developments in relational structures./01%3A_Set_Theory/1.01%3A_Set_Notation_and_Relations) The power set of a set $A$A, comprising all subsets of $A$A, is conventionally written as $\mathcal{P}(A)$P(A) or $P(A)$P(A), reflecting the exponential cardinality $2^{|A|}$2∣A∣; this notation gained prominence in axiomatic treatments post-1900./01%3A_Set_Theory/1.01%3A_Set_Notation_and_Relations) Sets are typically denoted by uppercase letters (e.g., $A$A, $B$B) to distinguish them from individual elements, which use lowercase letters (e.g., $a$a, $b$b), a convention that promotes clarity in expressions and has been standard in mathematical literature since the mid-20th century./01%3A_Set_Theory/1.01%3A_Set_Notation_and_Relations) The universe of discourse, the ambient collection over which quantifiers range, is often specified as the natural numbers $\mathbb{N}$N, the real numbers $\mathbb{R}$R, or the von Neumann universe $V$V, a cumulative hierarchy constructed via iterated power sets starting from the empty set, as formalized in the 1920s./01%3A_Set_Theory/1.01%3A_Set_Notation_and_Relations) For subsets of the reals, interval notations such as $[a, b] = \{ x \in \mathbb{R} \mid a \leq x \leq b \}$[a,b]={x∈R∣a≤x≤b}, $(a, b) = \{ x \in \mathbb{R} \mid a < x < b \}$(a,b)={x∈R∣a<x<b}, $[a, b) = \{ x \in \mathbb{R} \mid a \leq x < b \}$[a,b)={x∈R∣a≤x<b}, and $(a, b] = { x \in \mathbb{R} \mid a < x \leq b }$ provide compact representations, with square brackets indicating closed endpoints and parentheses open ones; these conventions originated in real analysis but are integral to set-theoretic descriptions of ordered structures./01%3A_Set_Theory/1.01%3A_Set_Notation_and_Relations) Subsets defined by properties are expressed using set-builder notation, $\{ x \in A \mid P(x) \}${x∈A∣P(x)}, where $P(x)$P(x) is a predicate satisfied by elements $x$x of $A$A; the curly braces $\{ \}${} for denoting sets were introduced by Zermelo in 1907 to formalize comprehension principles.^[9] In modern typesetting, such as LaTeX, these symbols are rendered via commands like $\in$∈, $\subseteq$⊆, $\cup$∪, and $\cap$∩, ensuring consistent appearance in published works since the widespread adoption of computer-based mathematical composition in the late 20th century./01%3A_Set_Theory/1.01%3A_Set_Notation_and_Relations)

History

Origins and Early Development

The roots of set theory can be traced to ancient and medieval philosophical discussions on collections and categories, though these were not formalized as mathematical theories. In ancient Greece, Aristotle's Categories (c. 350 BCE) provided a framework for classifying entities into types, distinguishing between substances and aggregates, which laid conceptual groundwork for later ideas of classes and groupings. Similarly, in Indian philosophy, the Nyāya school (c. 2nd century BCE onward) developed logic involving relational predicates for collections, analyzing how multiple items form unified wholes without invoking modern set aggregates, as seen in works like the Nyāya Sūtras. These precursors emphasized logical structures of groupings but did not address infinity mathematically. The 19th century marked the emergence of set theory through rigorous treatments of infinite collections. Bernhard Bolzano, in his posthumously published Paradoxien des Unendlichen (1851), defended the existence of actual infinities and demonstrated that certain infinite sets, such as the natural numbers and the even numbers, could be placed in one-to-one correspondence despite one being a proper subset of the other, challenging intuitive notions of size.^[10] This work anticipated key ideas in cardinality without fully developing them. Independently, Georg Cantor began exploring sets in the context of analysis during the 1870s, motivated by problems in Fourier series representation of functions, where he investigated the uniqueness of trigonometric expansions and encountered the need to compare the "sizes" of infinite point sets on the real line.^[11] Cantor's seminal 1874 paper, "Über eine Eigenschaft des Inbegriffes aller reellen algebraischen Zahlen," published in Journal für die reine und angewandte Mathematik, introduced the concept of set cardinality by showing that the set of real numbers has a greater cardinality than the set of natural numbers, using a nested interval argument to prove the uncountability of the reals. In 1891, he introduced the diagonal argument in another paper to explicitly demonstrate that the cardinality of the continuum, denoted $2^{\aleph_0}$2ℵ0​, exceeds $\aleph_0$ℵ0​, the cardinality of the naturals. Cantor's 1883 monograph Grundlagen einer allgemeinen Mannigfaltigkeitslehre further developed transfinite numbers, introducing ordinal numbers (like $\omega$ω for the order type of the naturals) via well-ordering principles and cardinal numbers ($\kappa$κ) to measure set sizes beyond finite ones.^[11] Concurrently, Richard Dedekind contributed foundational ideas; in his 1872 pamphlet Stetigkeit und irrationale Zahlen, he defined real numbers using "cuts" or partitions of the rationals into chains satisfying certain order properties, providing a set-theoretic construction of the continuum. Dedekind's 1888 essay Was sind und was sollen die Zahlen? extended this by axiomatizing natural numbers as a set with inductive structure. These developments profoundly influenced real analysis. Cantor's set-theoretic insights resolved issues in Bernhard Riemann's 1854 work on trigonometric series by clarifying the pathology of point sets, while Karl Weierstrass's epsilon-delta definitions of limits (from his 1870s lectures) incorporated set notions for rigorous continuity, paving the way for modern integration theory.

Naive Set Theory and Paradoxes

Naive set theory emerged in the late 19th century as an intuitive framework for handling infinite collections, building on Georg Cantor's pioneering work in transfinite numbers. It relied on the unrestricted comprehension principle, which asserts that for any definable property $P$P, there exists a set comprising all objects satisfying $P$P, denoted $\{x \mid P(x)\}${x∣P(x)}. This approach allowed unrestricted set formation, including the notion of a universal set $V$V containing all sets, and treated membership $\in$∈ as a primitive relation without foundational restrictions. However, this informality soon revealed deep inconsistencies, prompting a crisis in the foundations of mathematics. The first major paradox arose in 1897 with Cesare Burali-Forti's antinomy concerning ordinals. Burali-Forti considered the set $Y = \{x \mid x$Y={x∣x is an ordinal$\}$}, which, by the properties of ordinals, should itself be an ordinal and thus the largest ordinal. Yet, this leads to a contradiction because the ordinals are well-ordered, implying no such maximal ordinal exists, as every ordinal has a successor. This paradox highlighted issues with assuming the collection of all ordinals forms a set. Independently, in 1899, Georg Cantor discovered a related inconsistency, known as Cantor's paradox or the power set paradox. Considering the universal set $V$V of all sets, Cantor noted that its power set $\mathcal{P}(V)$P(V)—the set of all subsets of $V$V—must have a strictly larger cardinality than $V$V by his theorem on cardinalities. However, if $V$V contains all sets, then $\mathcal{P}(V)$P(V) should be a subset of $V$V, yielding an impossible cardinality comparison.^[12] The most famous contradiction, Russell's paradox, was formulated by Bertrand Russell in 1901 and dramatically illustrated the flaws in unrestricted comprehension. Russell defined the set $R = \{x \mid x \notin x\}$R={x∣x∈/x}, the collection of all sets that do not contain themselves. The question of whether $R \in R$R∈R leads to a dilemma: if $R \in R$R∈R, then by definition $R \notin R$R∈/R; conversely, if $R \notin R$R∈/R, then $R$R satisfies the defining property and thus $R \in R$R∈R. This self-referential inconsistency exposed the dangers of naive set-building. In June 1902, Russell communicated the paradox to Gottlob Frege via letter, undermining Frege's ongoing project in Grundgesetze der Arithmetik (Volume II), where a similar comprehension axiom (Basic Law V) permitted such constructions; Frege acknowledged the letter's devastating impact in his reply, effectively halting his logicist program to derive arithmetic from pure logic.^[13] These paradoxes reverberated through mathematical logic, severely challenging logicism—the view that mathematics could be reduced to logic without set-theoretic assumptions—as pursued by Frege and later Russell and Alfred North Whitehead in Principia Mathematica. The antinomies demonstrated that naive comprehension generated outright contradictions, necessitating restrictions on set formation. In response, Ernst Zermelo developed an axiomatic system in 1908 that avoided paradoxes by limiting comprehension to subsets of existing sets, providing a foundation for consistent set theory. Meanwhile, David Hilbert, influenced by the foundational turmoil, launched his program in the 1920s to finitistically prove the consistency of formalized mathematics, including set theory, though this effort was later shown incomplete by Kurt Gödel's incompleteness theorems in 1931.^[14][15]

Axiomatic Foundations

The discovery of paradoxes in naive set theory, such as Russell's paradox, necessitated a formal axiomatic approach to avoid inconsistencies while preserving the utility of sets as a foundational tool for mathematics. In 1908, Ernst Zermelo introduced the first comprehensive axiomatic system for set theory in his paper "Untersuchungen über die Grundlagen der Mengenlehre I," published in Mathematische Annalen. This system comprised seven axioms: the axiom of extensionality, which states that two sets are equal if they have the same elements; the axiom of pairing, allowing the formation of a set containing any two given sets; the axiom of union, enabling the collection of all elements from sets within a given set; the axiom of the power set, guaranteeing the existence of the set of all subsets of a given set; the axiom of infinity, positing the existence of an infinite set; and the axiom schema of separation, which permits subsets defined by properties from existing sets. Additionally, Zermelo included the axiom of choice as a separate principle to facilitate proofs like his well-ordering theorem. Zermelo's framework, while groundbreaking, faced criticisms for its reliance on an unrestricted separation schema that risked paradoxes and for lacking mechanisms to handle mappings between sets. In 1922, Abraham Fraenkel addressed these issues by proposing the axiom schema of replacement, which allows for the substitution of elements in a set according to a definable function, replacing the broader comprehension principle inherent in Zermelo's separation. This modification, independently suggested by Thoralf Skolem in the same year, strengthened the system by ensuring that the image of a set under a function remains a set, thus preventing the formation of improper classes. Skolem's contributions also highlighted the relativism of set-theoretic concepts, arguing in his 1922 address that notions like "uncountable" depend on the model of set theory, as countable models could satisfy the axioms yet interpret infinite sets differently from the "absolute" sense. The 1930s and 1940s saw further refinements through the work of John von Neumann, Paul Bernays, and Kurt Gödel, culminating in the Von Neumann–Bernays–Gödel (NBG) set theory. Von Neumann's 1925 axioms introduced proper classes to distinguish between sets and non-set collections, avoiding paradoxes by prohibiting classes from being elements of other classes. Bernays expanded this in the 1930s by formalizing a two-sorted theory with sets and classes as primitives, while Gödel streamlined it in 1940 for relative consistency proofs. This system provided a conservative extension of Zermelo-Fraenkel set theory, allowing class comprehension without risking inconsistency. Gödel's 1938 announcement of the constructible universe $L$L, a minimal model satisfying the axioms including the axiom of choice and the generalized continuum hypothesis, demonstrated the consistency of these principles relative to the axioms. Meanwhile, Alfred Tarski's work in the 1930s on truth definitions for formal languages laid groundwork for model-theoretic semantics in set theory. By the mid-20th century, Zermelo-Fraenkel set theory with the axiom of choice (ZFC) had emerged as the consensus standard, incorporating Fraenkel's replacement and other refinements into Zermelo's original framework. This acceptance was bolstered by Paul Cohen's 1963 development of forcing, which proved the independence of the continuum hypothesis from ZFC, shifting focus from consistency to the flexibility of axiomatic foundations.

Axiomatic Set Theory

Zermelo-Fraenkel Set Theory

Zermelo-Fraenkel set theory with the axiom of choice, commonly denoted ZFC, is the standard axiomatic system for set theory and serves as the foundational framework for modern mathematics. It consists of the standard axioms including schemas formulated as a first-order theory in the language with a single binary predicate symbol ∈, representing the membership relation. These axioms, building on Ernst Zermelo's 1908 system and refinements by Abraham Fraenkel and others, ensure the existence and properties of sets while avoiding the paradoxes of naive set theory. ZFC's structure allows for the rigorous development of mathematics by treating all mathematical objects as sets or definable from sets.^[16] The universe of sets in ZFC is conceptualized through the cumulative hierarchy $\{V_\alpha \mid \alpha \in \mathrm{Ord}\}${Vα​∣α∈Ord}, constructed by transfinite recursion along the class of ordinals. This hierarchy begins with $V_0 = \emptyset$V0​=∅, proceeds to successor stages $V_{\alpha+1} = \mathcal{P}(V_\alpha)$Vα+1​=P(Vα​) where $\mathcal{P}$P denotes the power set operation, and for limit ordinals $\lambda$λ, defines $V_\lambda = \bigcup_{\beta < \lambda} V_\beta$Vλ​=⋃β<λ​Vβ​. The full universe is then $V = \bigcup_{\alpha \in \mathrm{Ord}} V_\alpha$V=⋃α∈Ord​Vα​, comprising all well-founded sets built iteratively from the empty set. This stratified construction reflects the iterative conception of sets, where each stage contains all subsets of previous stages, enabling the encoding of complex structures.^[16] In ZFC, every set is well-founded, meaning there are no infinite descending membership chains $\dots \in x_2 \in x_1 \in x_0$⋯∈x2​∈x1​∈x0​. The axiom of regularity enforces this by ensuring every non-empty set has an element disjoint from it. Consequently, each set $x$x admits a rank function $\rho(x) = \min\{\alpha \mid x \subseteq V_\alpha\}$ρ(x)=min{α∣x⊆Vα​}, which assigns to $x$x the least ordinal $\alpha$α such that $x$x is contained in the $\alpha$α-th stage of the hierarchy. This rank measures the "depth" of $x$x in the membership relation and facilitates transfinite induction and recursion on sets.^[16] ZFC proves fundamental results in set theory, such as Cantor's theorem, which asserts that for any set $A$A, the power set $\mathcal{P}(A)$P(A) has strictly greater cardinality than $A$A, i.e., $|A| < |\mathcal{P}(A)|$∣A∣<∣P(A)∣. This theorem underpins the existence of uncountably many sets and the hierarchy of infinite cardinals. However, ZFC cannot decide certain key statements; notably, the Continuum Hypothesis (CH)—which posits that there is no cardinal between the cardinality of the natural numbers $\aleph_0$ℵ0​ and the continuum $2^{\aleph_0}$2ℵ0​—is independent of ZFC. Kurt Gödel proved in 1940 that CH is consistent with ZFC assuming ZFC's consistency, while Paul Cohen showed in 1963 using forcing that the negation of CH is also consistent with ZFC.^[16][17] As the dominant foundation, ZFC enables the reduction of all mathematical disciplines to set theory by encoding primitive notions like natural numbers (via von Neumann ordinals), functions (as sets of ordered pairs), and relations (as subsets) directly within its framework. This universality allows theorems in algebra, analysis, topology, and beyond to be interpreted set-theoretically, providing a unified logical basis while accommodating both classical and non-standard developments.^[16]

Key Axioms of ZFC

The Zermelo–Fraenkel axioms with the axiom of choice, known as ZFC, form the standard axiomatic foundation for set theory, comprising the core axioms including schemas that ensure the existence and properties of sets while avoiding paradoxes. These axioms, developed primarily between 1908 and 1930, provide a rigorous framework for mathematical reasoning by specifying how sets are identified, constructed, and related.^[18] The Axiom of Extensionality asserts that two sets are equal if and only if they have precisely the same elements, formalized as: $$\forall x \forall y \left( \forall z (z \in x \leftrightarrow z \in y) \to x = y \right).$$∀x∀y(∀z(z∈x↔z∈y)→x=y). This axiom, introduced by Ernst Zermelo, establishes a clear criterion for set identity based solely on membership, ensuring that sets are uniquely determined by their contents without ambiguity.^[18] It serves as the foundational principle for distinguishing sets and underpins all subsequent constructions in set theory. The Axiom of the Empty Set guarantees the existence of a set containing no elements, stated as: $$\exists x \forall y (y \notin x).$$∃x∀y(y∈/x). Proposed by Zermelo, this axiom provides the starting point for building all other sets, as the empty set acts as the initial object in iterative constructions like the natural numbers.^[18] Without it, the universe of sets would lack a minimal element, hindering basic set-building processes. The Axiom of Pairing allows the formation of a set from any two given sets, given by: $$\forall x \forall y \exists z (x \in z \land y \in z \land \forall w (w \in z \to w = x \lor w = y)).$$∀x∀y∃z(x∈z∧y∈z∧∀w(w∈z→w=x∨w=y)). Zermelo included this to enable the creation of finite sets from existing ones, facilitating the step-by-step assembly of more complex structures like ordered pairs essential for defining relations and functions.^[18] The Axiom of Union ensures that for any set of sets, there exists a set containing all elements from its members, formalized as: $$\forall x \exists y \forall z (z \in y \leftrightarrow \exists w (z \in w \land w \in x)).$$∀x∃y∀z(z∈y↔∃w(z∈w∧w∈x)). This Zermelo axiom supports operations that flatten hierarchies of sets, such as combining collections into a single domain, which is crucial for defining unions in mathematical proofs.^[18] The Axiom Schema of Separation (or Restricted Comprehension) states that for any set and any property definable by a formula φ(z), there exists a subset consisting of those elements of the set satisfying φ; for a formula φ(z), it is: $$\forall a \exists b \forall z (z \in b \leftrightarrow z \in a \land \phi(z)).$$∀a∃b∀z(z∈b↔z∈a∧ϕ(z)). Introduced by Zermelo, this schema allows the safe formation of subsets without leading to paradoxes like Russell's, by restricting comprehension to existing sets, and is essential for deriving basic sets like the empty set.^[19] The Axiom of the Power Set posits that every set has a set of all its subsets, expressed as: $$\forall x \exists y \forall z (z \in y \leftrightarrow \forall w (w \in z \to w \in x)).$$∀x∃y∀z(z∈y↔∀w(w∈z→w∈x)). Zermelo's inclusion of this axiom allows the generation of exponentially larger sets, enabling the representation of all possible subsets and thus supporting concepts like the continuum and Boolean algebras.^[18] The Axiom of Infinity asserts the existence of an infinite set, typically containing the empty set and closed under the successor operation, stated as: $$\exists x (\emptyset \in x \land \forall y \in x (y \cup \{y\} \in x)).$$∃x(∅∈x∧∀y∈x(y∪{y}∈x)). Zermelo introduced this to ensure the theory accommodates infinite collections, such as the natural numbers, which are indispensable for arithmetic and analysis.^[18] The Axiom Schema of Replacement is an infinite collection of axioms stating that if a definable function maps elements of a set to unique outputs, then the image forms a set; for a formula $\phi(x, y)$ϕ(x,y), it is: $$\forall a \left( \forall x \in a \exists ! y \, \phi(x, y) \to \exists b \forall y (y \in b \leftrightarrow \exists x \in a \, \phi(x, y)) \right).$$∀a(∀x∈a∃!yϕ(x,y)→∃b∀y(y∈b↔∃x∈aϕ(x,y))). Independently proposed by Abraham Fraenkel and Thoralf Skolem, this schema extends the theory to handle substitutions that produce arbitrarily large sets, such as transfinite ordinals, preventing limitations in set comprehension.^[18] The Axiom of Foundation (or Regularity) prohibits infinite descending chains of membership, formalized as: $$\forall x (x \neq \emptyset \to \exists y \in x (y \cap x = \emptyset)).$$∀x(x=∅→∃y∈x(y∩x=∅)). Originally formulated by John von Neumann and adopted by Zermelo, this axiom ensures the set membership relation is well-founded, preventing cycles or loops that could lead to paradoxical structures like Russell's set.^[18] The Axiom of Choice guarantees a choice function for any collection of nonempty sets, formalized as: $$\forall x \left( \forall y \in x (y \neq \emptyset) \to \exists f \left( f \text{ is a function} \land \forall y \in x (f(y) \in y) \right) \right).$$∀x(∀y∈x(y=∅)→∃f(f is a function∧∀y∈x(f(y)∈y))). Zermelo axiomatized this principle to formalize selections from infinite families, enabling well-orderings and results like the comparability of cardinals, though it remains independent of the other axioms.^[18]

Extensions and Alternatives

One prominent extension to Zermelo-Fraenkel set theory with choice (ZFC) is the axiom of constructibility, denoted $V = L$V=L, introduced by Kurt Gödel in 1938. This axiom asserts that every set is constructible, meaning it belongs to the innermost model $L$L built hierarchically from the empty set using definable power sets at each level. Gödel proved that $V = L$V=L is consistent relative to ZFC and implies both the axiom of choice and the generalized continuum hypothesis (GCH), which states that for every infinite cardinal $\kappa$κ, the cardinality of the power set of $\kappa$κ is the next cardinal after $\kappa$κ, i.e., $2^\kappa = \kappa^+$2κ=κ+. Large cardinal axioms provide stronger extensions beyond ZFC by positing the existence of cardinals with properties unattainable in standard models. An inaccessible cardinal $\kappa$κ is an uncountable regular strong limit cardinal, meaning it is regular (cannot be written as a union of fewer than $\kappa$κ sets each of size less than $\kappa$κ) and a strong limit (for any $\lambda < \kappa$λ<κ, $2^\lambda < \kappa$2λ<κ), exceeding all smaller cardinals in a way that cannot be "reached" from below using ZFC operations. Stronger still, a measurable cardinal $\kappa$κ admits a non-principal $\kappa$κ-complete ultrafilter $U$U on $\kappa$κ, or equivalently, there exists an elementary embedding $j: V \to M$j:V→M with critical point $\kappa$κ such that $M$M is closed under $\kappa$κ sequences. These axioms are consistent relative to even larger cardinals and play a key role in ongoing research into the limits of ZFC. Alternative foundational systems diverge from ZFC's well-founded structure. Willard Van Orman Quine's New Foundations (NF), proposed in 1937, replaces ZFC's axioms with a single stratified comprehension axiom, allowing sets to be formed from formulas where type variables are properly stratified to avoid paradoxes like Russell's, while permitting a universal set. This system supports much of classical mathematics but remains unproven consistent. Hyperset theory, developed by Peter Aczel in 1988, relaxes the axiom of foundation to accommodate non-well-founded sets, where infinite descending membership chains like $x \in x$x∈x are possible; Aczel's anti-foundation axiom ($\neg$¬Foundation) ensures every extensional graph has a unique hyperset realization, enabling applications in computer science such as modeling circular data structures.^[20] Post-2000 research has revisited set theories incorporating urelements (atoms), which are non-set individuals without elements, extending ZFC or ZF to include them via modified extensionality. For instance, recent work explores models where urelements form a separate sort, preserving choice while addressing philosophical motivations like nominalism in set ontology. Regarding independence, ZFC + $V = L$V=L proves the continuum hypothesis (CH), but ZFC extended by large cardinal axioms is consistent relative to stronger theories, and such extensions contradict $V = L$V=L, implying CH is false in models where $V \neq L$V=L.^[21]

Philosophical Aspects

Ontology of Sets

The ontology of sets concerns the metaphysical nature of sets as mathematical objects, addressing whether they exist independently of human thought or merely as formal constructs within theories. Philosophers of mathematics debate the status of sets, ranging from views that posit their objective reality to those that treat them as devoid of intrinsic meaning. These discussions often intersect with interpretations of axiomatic systems like Zermelo-Fraenkel set theory (ZF), where sets form a hierarchical structure known as the von Neumann universe $V$V, but the focus here is on the underlying philosophical commitments rather than the axioms themselves.^[22] Platonism, a prominent realist position, regards sets as abstract, timeless entities that exist independently of any mind or language, much like Platonic forms. Kurt Gödel championed this view, arguing that mathematics, including set theory, describes an objective reality of sets that we access through intuition, akin to perceiving physical objects. In his revised essay on the continuum hypothesis, Gödel emphasized that the universe of sets is a determinate structure, and our knowledge of it derives from a non-sensory perception of these abstract objects, countering nominalist objections by likening mathematical intuition to empirical perception. This platonist ontology commits set theory to the independent existence of the $V$V hierarchy, where sets are discovered rather than invented. In contrast, formalism denies any ontological commitment to sets beyond their role as syntactic elements in a formal system. David Hilbert, the leading formalist, viewed mathematics as a game of symbols manipulated according to rules, without reference to external realities; sets, in this framework, are merely configurations of meaningless signs whose consistency can be proven finitarily. In his 1925 address "On the Infinite," Hilbert distinguished between finitary mathematics, grounded in concrete intuitions of symbols, and ideal mathematics, including infinite sets, which serves as a useful fiction but carries no metaphysical weight. This approach avoids paradoxes by treating set theory as a consistent calculus, not a description of an independent domain, aligning with Hilbert's program to secure mathematics through metamathematical proofs. The iterative conception offers a middle ground, portraying sets as built cumulatively in transfinite stages from urelements (non-set atoms) or pure sets starting from the empty set, yielding the $V$V hierarchy without assuming prior ontological independence. George Boolos articulated this view in detail, defining a set as any collection formed at some stage of a process where earlier stages provide elements for later ones, ensuring no set contains itself and avoiding circularity. This conception justifies most ZF axioms—such as extensionality, pairing, union, power set, infinity, foundation, and separation—by reflecting a natural, staged formation process, while replacement follows from a maximality principle that all possible sets at a stage are included. Philosophically, it emphasizes sets' relational structure over intrinsic properties, providing an intuitive ontology that aligns with axiomatic set theory's cumulative hierarchy.^[22][22][22] Paul Benacerraf's 1965 identification problem challenges realist ontologies by highlighting the ambiguity in identifying specific mathematical objects across isomorphic models. In "What Numbers Could Not Be," Benacerraf argued that standard set-theoretic constructions of natural numbers—such as von Neumann ordinals (where $0 = \emptyset$0=∅, $1 = \{\emptyset\}$1={∅}, etc.) or Zermelo ordinals (where $0 = \emptyset$0=∅, $1 = \{\emptyset\}$1={∅}, $2 = \{\emptyset, \{\emptyset\}\}$2={∅,{∅}}, etc.)—are arbitrary, as any isomorphic structure satisfying the Peano axioms could serve equally well, yet no criterion distinguishes one as "the" numbers. This underdetermination extends to sets, implying that multiple models of set theory can be isomorphic yet differ in their "internal" identifications of objects, undermining claims of a unique ontology for the set-theoretic universe and favoring structuralist interpretations over objectivist ones. Structuralism, as developed by George Boolos in the 1980s, resolves such identification issues by defining sets not by their intrinsic nature but by their structural roles within the theory. Boolos proposed a two-sorted axiomatic system $S$S in his 1989 paper "Iteration Again," distinguishing "sets" from "stages" to capture the iterative process structurally, where sets occupy positions in a hierarchy defined by membership relations rather than being concrete entities. This approach treats the set-theoretic universe as a system of positions and relations, compatible with the iterative conception while avoiding Benacerraf's problem by focusing on isomorphism-invariant properties; thus, sets exist only as placeholders in the structure, providing an ontology that prioritizes mathematical practice over metaphysical commitments.

Controversies in Foundations

One of the central controversies in set theory foundations revolves around the Axiom of Choice (AC), which asserts that for any collection of nonempty sets, there exists a choice function selecting one element from each set. While AC facilitates many proofs in classical mathematics, it enables non-constructive existence arguments that critics argue lack explicit constructions, raising philosophical concerns about the nature of mathematical objects. A striking illustration is the Banach-Tarski paradox, which demonstrates that a solid ball in three-dimensional space can be decomposed into finitely many pieces and reassembled into two balls identical to the original, relying on AC to construct non-measurable sets that defy intuitive notions of volume preservation. This result, first proved in 1924, highlights how AC leads to counterintuitive outcomes, prompting debates on whether such non-constructive proofs undermine the reliability of set-theoretic foundations. The Continuum Hypothesis (CH), positing that there is no cardinal between the cardinality of the natural numbers $\aleph_0$ℵ0​ and the continuum $2^{\aleph_0}$2ℵ0​, represents another foundational flashpoint. Paul Cohen's 1963 forcing technique established CH's independence from Zermelo-Fraenkel set theory with Choice (ZFC), showing it neither provable nor disprovable within this framework, thus shifting focus to what constitutes a "natural" value for $2^{\aleph_0}$2ℵ0​. Ongoing debates question whether CH should hold in an ultimate set-theoretic universe, with efforts like Saharon Shelah's pcf theory from the 1980s providing bounds on cardinal invariants related to $2^{\aleph_0}$2ℵ0​, such as limiting the possible cofinalities in products of cardinals without assuming CH. More recently, in the 2020s, W. Hugh Woodin's work on the "ultimate L" conjecture—a generalization of Gödel's constructible universe—suggests that CH is true in this refined inner model, incorporating large cardinals while resolving inconsistencies.^[23][24] The axiom V = L, introduced by Kurt Gödel in 1938, posits that every set is constructible from simpler sets via a definable hierarchy, resolving CH affirmatively and ensuring a well-ordering of the reals. Proponents value V = L for its simplicity and determinacy implications, but critics, particularly advocates of large cardinal axioms, contend it is "too weak," as it contradicts the existence of measurable cardinals and other strong infinitary principles central to modern set theory. This tension underscores broader disputes on whether foundations should prioritize constructibility or embrace richer, potentially inconsistent structures from large cardinals. Intuitionism, championed by L. E. J. Brouwer in the early 20th century, rejects classical set theory's acceptance of non-effective sets and the law of excluded middle, insisting that mathematical existence requires explicit constructions. Brouwer viewed classical proofs relying on AC or impredicative definitions as invalid, arguing they introduce non-intuitive infinities detached from mental constructions, thus challenging the foundational status of ZFC and advocating a reformulation of set theory limited to effective, choice-free operations.

Applications

In Mathematics

Set theory serves as the foundational framework for much of modern mathematics, providing the primitive notions and structures from which other mathematical objects are constructed. All mathematical entities, from numbers to geometric spaces, can be encoded as sets within axiomatic systems like ZFC. This encoding ensures that mathematical reasoning is rigorous and consistent, allowing diverse branches to share a common language. For instance, basic operations on sets, such as unions and intersections, underpin the definitions of more complex structures across algebra, analysis, and topology. The construction of number systems exemplifies set theory's role in building arithmetic foundations. Natural numbers are defined using von Neumann ordinals, where the empty set ∅ represents 0, {∅} represents 1, {∅, {∅}} represents 2, and each successor is obtained by adding the previous ordinal to the current set, yielding an infinite well-ordered chain isomorphic to the naturals. Integers arise as equivalence classes of pairs of natural numbers (a, b) representing a - b, with equivalence under (a, b) ~ (c, d) if a + d = b + c. Rational numbers are similarly constructed as equivalence classes of pairs of integers (p, q) with q ≠ 0, under (p, q) ~ (r, s) if p s = q r. Real numbers can be formed via Dedekind cuts, partitioning the rationals into lower and upper sets L and U such that L ∪ U = ℚ, L < U (every element of L is less than every element of U), and L has no greatest element. Alternatively, reals are equivalence classes of Cauchy sequences of rationals, where a sequence (q_n) is Cauchy if for every ε > 0 there exists N such that |q_m - q_n| < ε for m, n > N, and two sequences are equivalent if their difference converges to 0. In algebra, set-theoretic constructions formalize structures like groups, rings, and vector spaces. A group is a set G with a binary operation ⋅ : G × G → G satisfying closure, associativity ((a ⋅ b) ⋅ c = a ⋅ (b ⋅ c)), identity (∃ e ∈ G, ∀ a ∈ G, a ⋅ e = e ⋅ a = a), and inverses (∀ a ∈ G, ∃ a^{-1} ∈ G, a ⋅ a^{-1} = a^{-1} ⋅ a = e). Rings extend this with two operations, addition forming an abelian group and multiplication being associative and distributive. Vector spaces are sets V over a field F (itself a commutative ring with multiplicative inverses), closed under addition and scalar multiplication from F, satisfying linearity axioms. These definitions rely on the power set P(V) to specify operations as functions, ensuring algebraic properties are verifiable within set theory. Topology and analysis further illustrate set theory's ubiquity. A topological space is a set X with a collection τ ⊆ P(X) of open sets, where ∅, X ∈ τ, τ is closed under arbitrary unions, and finite intersections. This abstracts continuity and convergence without metrics. Metric spaces refine this: a set M with a distance function d : M × M → [0, ∞) satisfying positivity (d(x, y) = 0 iff x = y), symmetry, and triangle inequality (d(x, z) ≤ d(x, y) + d(y, z)). Compactness in metric spaces is defined as every open cover having a finite subcover, a property crucial for theorems like Heine-Borel, where closed bounded subsets of ℝ^n are compact. In category theory, sets serve as the objects in the category Set, with morphisms as functions; however, to handle large categories without size issues, set theory underlies via Grothendieck universes—transitive sets U closed under power sets and unions, containing all small sets needed for category operations. Cardinality provides a set-theoretic measure of size, equating sets via bijections: two sets A and B have the same cardinality |A| = |B| if there exists a bijection f : A → B. This extends to infinite sets, where countable infinity ℵ_0 matches the naturals, and the continuum 2^{ℵ_0} equals the reals, revealing uncountable infinities. Hilbert's infinite hotel paradox illustrates this: a hotel with countably infinite rooms, all occupied, can accommodate another guest by shifting occupants (room n to n+1), or infinitely many by more intricate bijections, demonstrating that countable infinities absorb equals without exhaustion.

In Computer Science and Logic

Set theory plays a foundational role in computer science and logic, providing the mathematical structures for data organization, type systems, and formal reasoning. In databases, the relational model treats tables as sets of tuples, enabling efficient querying and data integrity through set operations like union, intersection, and projection. This approach, introduced by Edgar F. Codd in 1970, revolutionized data management by formalizing relations as subsets of Cartesian products of domains, where each tuple represents an element with no duplicates, mirroring set membership.^[25] In type theory for programming languages, sets inform the distinction between sets and types to prevent paradoxes akin to Russell's, where types stratify expressions to avoid self-referential issues. Bertrand Russell's 1908 theory of types layered logical expressions to sidestep paradoxes like the set of all sets not containing themselves, influencing modern type systems that ensure well-formed computations.^[26] This separation extends to Hindley-Milner type inference, which uses polymorphic types—generalizing set-like universality—to automatically infer types in functional languages like ML, balancing expressiveness with safety without explicit annotations.^[27] In formal logic, set theory underpins model theory, where a model of a first-order theory is a structure $(M, I)$(M,I) consisting of a non-empty set $M$M as the universe and an interpretation function $I$I assigning meanings to symbols, allowing satisfaction of formulas via set-theoretic semantics. This framework evaluates logical truths by checking if sentences hold in all or some models, connecting syntax to set-based interpretations. Kurt Gödel's incompleteness theorems, proved in 1931, rely on encoding syntactic objects as natural numbers within sets, demonstrating that arithmetic cannot prove its own consistency, thus revealing limits in formal systems built on set foundations. Fuzzy set theory extends classical sets to handle vagueness in logic and computing, defining a fuzzy set on universe $X$X by a membership function $\mu: X \to [0,1]$μ:X→[0,1], where $\mu(x)$μ(x) indicates the degree of belonging rather than binary membership. Introduced by Lotfi A. Zadeh in 1965, fuzzy sets support operations like intersection via $\min(\mu_A(x), \mu_B(x))$min(μA​(x),μB​(x)) and union via $\max(\mu_A(x), \mu_B(x))$max(μA​(x),μB​(x)), enabling applications in control systems and approximate reasoning where crisp boundaries fail.^[28] Complementarity is defined as $\mu_{\overline{A}}(x) = 1 - \mu_A(x)$μA​(x)=1−μA​(x), preserving set-like algebraic properties while accommodating uncertainty. Building on this, rough set theory, developed by Zdzisław Pawlak in 1982, models imperfect knowledge using lower and upper approximations of sets based on equivalence relations, where the lower approximation includes elements certainly belonging to the set, and the upper includes possible members, aiding feature selection in AI without probabilistic assumptions.^[29] Recent advancements in quantum computing incorporate set concepts with superposition, allowing states to represent linear combinations of set configurations for parallel processing. For instance, quantum algorithms for set operations, such as intersection and difference, leverage amplitude amplification on superpositions of basis states encoding set elements, achieving speedups over classical methods for unstructured search problems. In computability theory, set theory classifies subsets of natural numbers as recursive (computably enumerable) or not, with the halting problem exemplified by the undecidable set of Turing machine indices that halt on empty input, as shown by Alan Turing in 1936, underscoring inherent limits in algorithmic decidability.^[30] This undecidability highlights how set-theoretic encodings reveal non-computable properties central to theoretical computer science.^[31]

Areas of Study

Combinatorial Set Theory

Combinatorial set theory investigates the combinatorial properties of infinite sets, particularly focusing on cardinalities, partition relations, and structures like stationary sets within the framework of Zermelo-Fraenkel set theory with choice (ZFC). It extends finite combinatorics to infinite domains, exploring how infinite structures inevitably contain highly ordered subsets despite arbitrary partitions. This field addresses questions about the sizes of sets and the unavoidable patterns in colorings or partitions of infinite objects, providing tools to bound cardinal arithmetic and analyze infinite graphs.^[32] A central area is partition calculus, which generalizes Ramsey's theorem to infinite sets. Ramsey's theorem states that in any 2-coloring of the edges of a sufficiently large complete graph, there exists a monochromatic clique of a given size; specifically, the Ramsey number $R(3,3) = 6$R(3,3)=6 means that any 2-coloring of the edges of the complete graph on 6 vertices contains a monochromatic triangle, while there exists a coloring of the graph on 5 vertices without one.^[33] For infinite sets, the Erdős–Rado theorem extends this by asserting partition relations such as $\aleph_1 \to (\aleph_0)^2_2$ℵ1​→(ℵ0​)22​, guaranteeing infinite monochromatic subsets in 2-colorings of the pairs from uncountable sets, with generalizations via the stepping-up lemma for larger cardinals. This result, proved using a stepping-up lemma, forms the foundation for infinite Ramsey theory.^[34] Stationary sets and club guessing principles further illuminate infinite combinatorics on ordinals. A subset $C \subseteq \kappa$C⊆κ (for a regular uncountable cardinal $\kappa$κ) is closed unbounded (club) if it is unbounded in $\kappa$κ—meaning for every $\alpha < \kappa$α<κ, there is $\beta \in C$β∈C with $\alpha < \beta$α<β—and closed under limits of sequences from $C$C with length less than $\kappa$κ. A set $S \subseteq \kappa$S⊆κ is stationary if it intersects every club subset of $\kappa$κ, capturing "large" sets that are unavoidable in certain partitions. Club guessing principles, such as those predicting the existence of sequences that "guess" clubs in a prescribed way, provide combinatorial axioms that imply bounds on cardinal characteristics and reflection properties.^[35][36] In the 1940s, Paul Erdős posed foundational problems on partition relations, such as determining when $\lambda \to (\alpha, \beta)^k$λ→(α,β)k holds for infinite cardinals $\lambda$λ and ordinals $\alpha, \beta$α,β, influencing the development of infinite combinatorics by highlighting gaps between finite and transfinite cases. Later, Saharon Shelah's pcf theory (possible cofinalities) addressed the singular cardinals problem by analyzing the cofinalities of reduced products of sets of regular cardinals, yielding bounds like $2^{\aleph_\omega} < \aleph_{\omega_4}$2ℵω​<ℵω4​​ under certain ideals, which constrain the power set cardinalities of singular cardinals.^[37][38] Cardinal arithmetic underpins these results, with addition of infinite cardinals satisfying $\kappa + \lambda = \max(\kappa, \lambda)$κ+λ=max(κ,λ) whenever at least one is infinite, simplifying computations for large sets. The cofinality $\mathrm{cf}(\kappa)$cf(κ) is the smallest cardinal $\mu$μ such that $\kappa$κ is the supremum of a sequence of length $\mu$μ from smaller ordinals, distinguishing regular cardinals (where $\mathrm{cf}(\kappa) = \kappa$cf(κ)=κ) from singular ones. Applications extend to graph theory, where infinite Ramsey theory ensures that every infinite tournament— a directed complete graph—contains an infinite transitive subtournament, aiding the study of orderings in infinite relational structures.^[32][39]

Descriptive Set Theory

Descriptive set theory is a branch of set theory that studies the definability and complexity of subsets of Polish spaces, focusing on hierarchies of sets generated by effective operations. Polish spaces are complete separable metric spaces, such as the Baire space $\mathbb{N}^\mathbb{N}$NN or the real line $\mathbb{R}$R, which provide a natural setting for analyzing topological and descriptive properties of sets.^[40] These spaces allow for the classification of sets based on their descriptive complexity, beginning with the Borel sets and extending to more complex classes like analytic and projective sets. The theory emphasizes regularity properties, such as measurability and the perfect set property, which hold for definable sets in these spaces.^[41] The Borel hierarchy classifies Borel sets, which are generated from the open sets through countable unions, intersections, and complements, indexed by countable ordinals. Specifically, the levels $\Sigma^0_\alpha$Σα0​ consist of countable unions of sets from previous $\Pi^0_\beta$Πβ0​ levels for $\beta < \alpha$β<α, while $\Pi^0_\alpha$Πα0​ are the complements of $\Sigma^0_\alpha$Σα0​ sets, and $\Delta^0_\alpha = \Sigma^0_\alpha \cap \Pi^0_\alpha$Δα0​=Σα0​∩Πα0​. This hierarchy is strict in uncountable Polish spaces, meaning each level properly extends the previous ones up to $\omega_1$ω1​. Borel sets form the foundation of descriptive set theory, as they exhibit desirable properties like Lebesgue measurability and the Baire property.^[40] Analytic sets, introduced by Mikhail Suslin in the 1920s, are the continuous images of Polish spaces and include all Borel sets but extend beyond them. Their complements, co-analytic sets, are also significant, and Suslin showed that analytic sets are measurable and have the perfect set property. A key early question was the Suslin's problem, posed by Suslin in 1920, asking whether every ccc linearly ordered set without endpoints is order-isomorphic to the reals; Wacław Sierpiński resolved this negatively in 1920 by constructing a counterexample.^[42][43] The projective hierarchy builds on analytic sets by applying existential and universal quantifiers over reals iteratively: $\Sigma^1_1$Σ11​ denotes analytic sets, $\Pi^1_1$Π11​ co-analytic sets, and higher levels $\Sigma^1_n$Σn1​ and $\Pi^1_n$Πn1​ alternate projections and complements. This hierarchy captures sets definable in second-order arithmetic and is central to understanding the limits of definability in the reals. Uniformization theorems, which guarantee selectable sections for relations in these classes, were advanced in the 1970s by Donald A. Martin, including results for $\Sigma^1_3$Σ31​ sets. Further progress came from Martin and John R. Steel in the 1980s, who established uniformization for all projective sets assuming projective determinacy.^[44] A pivotal result in the theory is the determinacy of games with Borel payoff sets, proved by Martin in 1975, which implies strong regularity properties for Borel sets without relying on the axiom of choice. This Borel determinacy theorem connects to broader themes in set theory, where higher levels of determinacy for projective sets require large cardinal assumptions, such as the existence of Woodin cardinals, to establish consistency with ZFC.^[45]

Large Cardinals and Forcing

Large cardinals represent a hierarchy of increasingly strong axioms extending ZFC set theory, positing the existence of cardinals with exceptional properties that imply the consistency of weaker axioms. A cardinal κ is weakly inaccessible if it is uncountable, regular, and a strong limit cardinal, meaning that for every λ < κ, 2^λ < κ.^[46] Strongly inaccessible cardinals are weakly inaccessible cardinals that are limits of inaccessible cardinals below them.^[46] A Mahlo cardinal is a regular cardinal κ such that the set of inaccessible cardinals below κ is stationary in κ.^[46] These notions form the base of the large cardinal hierarchy, with each level providing reflection principles and consistency strength beyond ZFC.^[46] Measurable cardinals mark a significant escalation, defined as a cardinal κ equipped with a normal ultrafilter U on κ, which induces a non-trivial elementary embedding j: V → M where M is a transitive inner model containing all ordinals, the critical point is κ, and M is closed under <κ sequences.^[46] Supercompact cardinals further strengthen this: a cardinal κ is supercompact if for every λ ≥ κ, there exists an elementary embedding j: V → M with critical point κ such that V_λ ⊆ M.^[46] Such embeddings ensure profound reflection properties across the universe. The constructible universe L, Gödel's inner model built by iterating definable power sets over ordinals, satisfies ZFC and the generalized continuum hypothesis but contains no large cardinals beyond what ZFC proves consistent.^[47] Forcing, introduced by Cohen, is a method to construct generic extensions of models of set theory, proving independence results by adding new sets while controlling their properties. A forcing poset P is a partial order with a greatest element 1_P, used to approximate sets in the extension; conditions p, q ∈ P satisfy p ≤ q if p extends q.^[48] A generic filter G ⊆ P over a model V is an ultrafilter intersecting every dense subset of P definable in V, ensuring G is "random" from V's perspective.^[47] Names Ṅ in V are elements of the forcing language, formal objects like pairs (Ṅ, ∈̇) representing sets in the extension, interpreted in V[G] via the canonical name for the empty set and recursive closure under the generic filter: the interpretation of a name τ is { (interpretation of σ, interpretation of ρ) | (σ, ρ) ∈ τ^G }, yielding the model V[G].^[47] Density arguments are central to forcing proofs: a subset D ⊆ P is dense if for every p ∈ P, there exists q ≤ p with q ∈ D, allowing one to show that generics meet certain conditions by ensuring the property holds in every extension.^[47] Forcing preserves cardinals when the poset satisfies the κ-chain condition (no antichains of size κ) for relevant κ, preventing collapses; for example, countable chain condition forcings preserve all cardinals and cofinalities.^[47] Cohen's 1963 application of forcing demonstrated the independence of the continuum hypothesis (CH) from ZFC by constructing a model where 2^{ℵ_0} = ℵ_2. He used the forcing poset Add(ω, ℵ_2), consisting of partial functions from ω × ℵ_2 to 2 with finite support and the extension order, which adds ℵ_2 many generic Cohen subsets of ω, making the powerset of ω have size ℵ_2 in the extension V[G], refuting CH while preserving ZFC axioms.^[48] Easton's 1970 theorem generalized this, showing that for any class of regular cardinals satisfying certain monotonicity and cofinality conditions, one can force the continuum function on regulars to match a prescribed Easton function using a product of forcings, yielding flexible cardinal arithmetic consistent with ZFC. Kunen's 1971 inconsistency theorem established that Reinhardt cardinals, defined via elementary embeddings j: V → V, cannot exist in ZFC, as such embeddings lead to a contradiction via the axiom of choice and ultrapower constructions.^[49] In the 1990s, Woodin developed Ω-logic, an infinitary logic using universally Baire sets to capture ultimate inner models, conjecturing V = Ultimate L, a canonical constructible-like model incorporating all large cardinals and resolving questions like the continuum hypothesis under strong determinacy assumptions.^[50]

Other Specialized Branches

Fuzzy set theory extends classical set theory by allowing elements to have degrees of membership between 0 and 1, rather than binary membership. Precursors to this idea appear in Jan Łukasiewicz's work on many-valued logics in the 1920s, where he developed three-valued logic to handle indeterminate propositions, laying groundwork for non-classical set structures. The modern formulation was introduced by Lotfi A. Zadeh in 1965, defining a fuzzy set $A$A on a universe $X$X via a membership function $\mu_A: X \to [0,1]$μA​:X→[0,1], where $\mu_A(x)$μA​(x) represents the degree to which $x$x belongs to $A$A. Operations on fuzzy sets, such as intersection and union, are generalized using triangular norms (t-norms) and t-conorms; for example, the standard intersection is the minimum t-norm $\min(a,b)$min(a,b), while the Łukasiewicz t-norm $T_L(a,b) = \max(0, a + b - 1)$TL​(a,b)=max(0,a+b−1) captures gradual overlap. These structures find applications in control theory, notably in Ebrahim Mamdani's 1974 fuzzy logic controller for dynamic systems, which uses rule-based inference to manage nonlinear processes like cement kiln operation without precise mathematical models. Inner model theory constructs canonical models within the universe of sets to analyze large cardinal assumptions and their consequences. A key concept is the hereditarily ordinal definable (HOD) sets, comprising all sets definable from ordinals without real parameters, forming the inner model HOD that captures definability in V. Fine-structural inner models, such as those built via Mitchell-Steel core model induction, extend L to include measures on large cardinals while preserving fine structure for iterability.^[51] Core models like K^c, developed in the 1980s, address failures of determinacy by incorporating extenders for Woodin cardinals, providing a minimal model where determinacy axioms fail in a controlled manner.^[52] The axiom of determinacy (AD) posits that in two-player games of perfect information on reals, one player has a winning strategy, contradicting the axiom of choice but implying strong regularity properties for sets of reals.^[46] Projective determinacy (PD), restricting AD to projective sets, follows from the existence of infinitely many Woodin cardinals, as proven by W. Hugh Woodin in the 1980s through iterability arguments linking large cardinals to scales in L(R).^[53] These results establish PD's consistency strength between measurable and supercompact cardinals, enabling analytic proofs of theorems like uniformization for projective sets.^[54] Cardinal invariants measure the size of the continuum relative to ideals on the reals, with the continuum $c = 2^{\aleph_0}$c=2ℵ0​ as a central value. The null-additivity number add(null) is the minimal cardinality of a family of null sets whose union is non-null, while cov(meager) is the minimal number of meager sets covering the reals.^[55] These invariants, along with others like non(null) and cof(null), are interconnected in Cichoń's diagram, which diagrams ZFC-provable inequalities such as add(null) ≤ cov(null) ≤ non(meager) ≤ cof(meager) ≤ c, originally outlined by Jacek Cichoń in 1979 and formalized in subsequent analyses.^[56] In set-theoretic topology, forcing axioms refine continuum hypothesis alternatives. Martin's Axiom (MA), introduced by Donald A. Martin and Robert M. Solovay in 1970, asserts that for ccc posets of size less than c, dense sets of size less than c have compatible elements, implying cov(meager) = c, meaning the reals cannot be covered by fewer than c meager sets. This enhances topological properties, such as making the union of c meager sets meager, and is consistent with c > ℵ₁ via Cohen forcing.^[57] Recent advances include Joan Bagaria's 2024 work on structural reflection, linking large cardinals to the Ultimate-L conjecture, positing an ultimate inner model L with all large cardinals below the least strongly compact.^[58] Paraconsistent set theories, explored since Newton C.A. da Costa's 1977 framework, allow inconsistent sets without explosion, enabling models of naive set theory where Russell's paradox holds non-trivially via relevance logic.^[59]

Education and Pedagogy

Role in Mathematical Curricula

In elementary and secondary education, set theory is introduced through intuitive tools like Venn diagrams and basic operations such as union, intersection, and complement, typically in grades 6-12 to build foundational logical reasoning skills.^[60] In the United States, the Common Core State Standards incorporate sets into the study of functions starting in grade 8, defining a function as a rule assigning each input from one set (the domain) to exactly one output in another set (the range), often illustrated with ordered pairs.^[61] This approach emphasizes conceptual understanding over rote computation, aligning with broader goals of mathematical literacy. The 1960s New Math movement in U.S. schools prominently featured set theory in elementary curricula to foster abstract thinking and discovery-based learning, supported by initiatives like the School Mathematics Study Group.^[62] However, it faced significant backlash by the early 1970s for its perceived excessive abstraction, which confused students and parents, leading to a rapid decline and a return to more traditional "back-to-basics" methods.^[62] At the undergraduate level, set theory forms a core component of discrete mathematics courses, where students learn the basics of Zermelo-Fraenkel set theory with choice (ZFC), including axioms, cardinal numbers, and their properties, to establish rigorous foundations for further study.^[5] These concepts are essential for proofs in analysis and algebra, such as demonstrating subset relations or equality of sets using inclusion-exclusion principles.^[63] In the 2020s, set theory has gained emphasis in computer science curricula, integrated into discrete structures knowledge areas to support algorithm design, data management, and complexity analysis, as outlined in recent global computing education guidelines such as CS2023, extending to applications in AI and data science.^[64] Graduate programs delve into advanced set theory topics, such as forcing techniques to explore independence results in logic seminars, building on ZFC to construct models that address questions like the continuum hypothesis.^[65] Set theory often appears in qualifying exams for PhD candidates in mathematics, testing proficiency in areas like transitive models, ordinals, and large cardinals to ensure readiness for research.^[66] Globally, European undergraduate programs tend to emphasize axiomatic set theory more deeply, with dedicated courses on Zermelo-Fraenkel axioms and their implications for mathematical foundations, as seen in curricula at institutions like the University of Edinburgh.^[67] In contrast, Asian programs, such as those at the University of Hong Kong, often prioritize applied aspects of set theory within discrete mathematics, focusing on practical implementations in computing and optimization.^[68]

Teaching Challenges and Methods

Teaching set theory presents several challenges, particularly for beginners encountering its abstract nature. The foundational concepts, such as sets and their operations, often lack concrete referents, making it difficult for students to build intuition without tangible examples.^[69] This abstractness is compounded by the counterintuitive aspects of infinite sets, where students struggle to reconcile finite experiences with concepts like uncountable infinities.^[70] Paradoxes further exacerbate these issues, as they reveal inconsistencies in naive set comprehension, such as Russell's paradox, which challenges students' preconceptions about self-referential sets and leads to confusion about foundational assumptions.^[71] The technicality of axiomatic systems like Zermelo-Fraenkel set theory with choice (ZFC) often results in rote memorization of axioms and proofs, hindering deeper conceptual understanding and promoting mechanical application over genuine insight.^[72] To address these challenges, educators employ various pedagogical methods tailored to enhance comprehension. Visual aids, such as Hasse diagrams, illustrate partial orders on sets by representing elements as points connected by lines indicating relations, omitting transitive edges for clarity and helping students visualize abstract hierarchies without overwhelming complexity.^[73] Formal proof assistants like Coq facilitate interactive verification of ZFC axioms and theorems, allowing students to construct and check proofs in a textbook-style environment with automated tactics, thereby bridging informal reasoning and rigorous deduction while requiring minimal prior knowledge of the tool. Inquiry-based learning approaches, particularly on paradoxes, encourage students to explore contradictions through guided problems, such as analyzing Russell's set of non-self-membered sets, fostering active discovery and resolution via axiomatic refinements.^[71] Historical influences, such as Jean Dieudonné's advocacy within the Bourbaki group during the 1970s, promoted rigorous axiomatic set theory in curricula, emphasizing structural foundations over intuitive geometry to cultivate precise mathematical thinking, though this sometimes intensified rote learning challenges.^[74] In contemporary settings, massive open online courses (MOOCs) incorporate interactive simulations to model cardinalities, enabling learners to manipulate infinite sets visually and experiment with bijections between countable and uncountable structures.^[75] Assessment in set theory education prioritizes proof-based tasks over definitional recall, such as demonstrating subset relations using element arguments—assuming an arbitrary element in one set and showing membership in the other—to verify properties like union distributivity, ensuring students apply concepts actively.^[76] Promoting inclusivity involves addressing diverse learners' misconceptions, particularly cultural perspectives on infinity, where some view it as a spiritual or processional limit rather than a completed mathematical entity, requiring educators to integrate cross-cultural examples to reframe infinity as a neutral, axiomatic construct and reduce barriers for non-Western students.^[77][78]