Hubbry Logo
Terminal and nonterminal symbolsTerminal and nonterminal symbolsMain
Open search
Terminal and nonterminal symbols
Community hub
Terminal and nonterminal symbols
logo
8 pages, 0 posts
0 subscribers
Be the first to start a discussion here.
Be the first to start a discussion here.
Terminal and nonterminal symbols
Terminal and nonterminal symbols
Terminal and nonterminal symbols
View on Wikipedia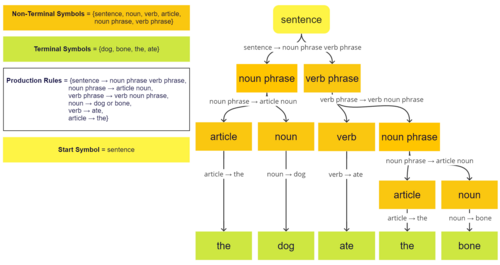
from Wikipedia
The string "the dog ate the bone" was created using production rules that replaced nonterminal with terminal symbols.[1]

In formal languages, terminal and nonterminal symbols are parts of the vocabulary under a formal grammar. Vocabulary is a finite, nonempty set of symbols. Terminal symbols are symbols that cannot be replaced by other symbols of the vocabulary. Nonterminal symbols are symbols that can be replaced by other symbols of the vocabulary by the production rules under the same formal grammar.[2]

A formal grammar defines a formal language over the vocabulary of the grammar.

In the context of formal language, the term vocabulary is more commonly known as alphabet. Nonterminal symbols are also called syntactic variables.

Terminal symbols

[edit]

Terminal symbols are those symbols that can appear in the formal language defined by a formal grammar. The process of applying the production rules successively to a start symbol might not terminate, but if it terminates when there is no more production rule can be applied, the output string will consist only of terminal symbols.

For example, consider a grammar defined by two rules. In this grammar, the symbol Б is a terminal symbol and Ψ is both a nonterminal symbol and the start symbol. The production rules for creating strings are as follows:

  1. The symbol Ψ can become БΨ
  2. The symbol Ψ can become Б

Here Б is a terminal symbol because no rule exists to replace it with other symbols. On the other hand, Ψ has two rules that can change it, thus it is nonterminal. The rules define a formal language that contains countably infinite many finite-length words by the fact that we can apply the first rule any countable times as we wish. Diagram 1 illustrates a string that can be produced with this grammar.

Diagram 1. The string Б Б Б Б was formed by the grammar defined by the given production rules. This grammar can create strings with any number of the symbol Б

Nonterminal symbols

[edit]

Nonterminal symbols are those symbols that cannot appear in the formal language defined by a formal grammar. A formal grammar includes a start symbol, which is a designated member of the set of nonterminal symbols. We can derive a set of strings of only terminal symbols by successively applying the production rules. The generated set is a formal language over the set of terminal symbols.

Context-free grammars are those grammars in which the left-hand side of each production rule consists of only a single nonterminal symbol. This restriction is non-trivial; not all languages can be generated by context-free grammars. Those that can are called context-free languages. These are exactly the languages that can be recognized by a non-deterministic push down automaton. Context-free languages are the theoretical basis for the syntax of most programming languages.

Production rules

[edit]

A grammar is defined by production rules (or just 'productions') that specify which symbols can replace which other symbols; these rules can be used to generate strings, or to parse them. Each such rule has a head, or left-hand side, which consists of the string that can be replaced, and a body, or right-hand side, which consists of a string that can replace it. Rules are often written in the form head → body; e.g., the rule a → b specifies that a can be replaced by b.

In the classic formalization of generative grammars first proposed by Noam Chomsky in the 1950s,[3][4] a grammar G consists of the following components:

  • A finite set N of nonterminal symbols.
  • A finite set Σ of terminal symbols that is disjoint from N.
  • A finite set P of production rules, each rule of the form
where denotes the set of all possible finite-length strings over the vocabulary using Kleene star. That is, each production rule replaces one string of symbols that contains at least one nonterminal symbol with another. In the case that the body consists solely of the empty string[note 1], it can be denoted with a special notation (often Λ, e or ε) to avoid confusion.
  • A distinguished symbol that is the start symbol.

A grammar is formally defined as the ordered quadruple . Such a formal grammar is often called a rewriting system or a phrase structure grammar in the literature.[5][6]

Example

[edit]

Backus–Naur form is a notation for expressing certain grammars. For instance, the following production rules in Backus-Naur form are used to represent an integer (which can be signed): 

<digit> ::= '0' | '1' | '2' | '3' | '4' | '5' | '6' | '7' | '8' | '9'
<integer> ::= ['-'] <digit> {<digit>}

In this example, terminal symbols are , and nonterminal symbols are <digit>, <integer>. [note 2]

Another example is:

In this example, terminal symbols are , and nonterminal symbols are .

See also

[edit]

Notes

[edit]

References

[edit]
Revisions and contributorsEdit on WikipediaRead on Wikipedia

Terminal and nonterminal symbols

View on Grokipedia
from Grokipedia
In theory, terminal and nonterminal symbols are the core building blocks of a , which is a mathematical system for defining the syntax of a as a set of strings over an . Terminals, often denoted by lowercase letters or specific lexical tokens like keywords and operators, represent the indivisible atomic units that form the final output strings of the language and cannot be further expanded or replaced. In contrast, nonterminals, typically uppercase letters or enclosed in angle brackets (e.g., ), serve as variables or placeholders for that can be recursively substituted via production rules to generate valid sentences. A formal grammar is formally defined as a four-tuple G = (N, T, P, S), where N is the finite set of nonterminal symbols, T is the finite set of terminal symbols (with N and T disjoint), P is a finite set of production rules of the form α → β (where α and β are strings of symbols from N ∪ T, α is non-empty and contains at least one nonterminal, and β may be empty), and S ∈ N is the distinguished start symbol from which derivation begins. In context-free grammars, a common type, α consists of exactly one nonterminal. These components enable the grammar to generate all valid strings in the language L(G) through successive applications of productions, starting from S and replacing (parts containing) nonterminals until only terminals remain, or conversely, to recognize and parse input strings by reducing them back to S. Terminal and nonterminal symbols are particularly prominent in context-free grammars (CFGs), a type of Type-2 grammar in the Chomsky hierarchy, which are widely used to specify the syntax of programming languages in compilers and parsers. For instance, in a simple arithmetic expression grammar, terminals might include operators like + and digits like 0-9, while nonterminals such as Expr and Term allow hierarchical structuring (e.g., Expr → Expr + Term | Term). This distinction ensures unambiguous syntactic analysis, supporting applications in natural language processing, automated theorem proving, and software engineering tools, though it focuses solely on structure without addressing semantics.

Core Definitions

Terminal symbols

Terminal symbols, also known as terminals, are the literal characters, tokens, or primitives that constitute the final strings generated by a formal grammar and cannot be further replaced or expanded by production rules. They form the basic alphabet Σ\Sigma of the language defined by the grammar, serving as the irreducible building blocks that appear directly in the output sentences or words. In contrast to nonterminal symbols, which are placeholders subject to substitution, terminals mark the endpoints of any derivation process. In the structure of a derivation tree, terminal symbols occupy the leaf nodes, where the expansion of nonterminals ceases, yielding the complete of the . Once a terminal is introduced in a sentential form, it remains immutable throughout the remainder of the derivation, ensuring that the produces only valid sequences over its without further decomposition. This fixed nature distinguishes terminals as the concrete output elements, often including digits, , or keywords in practical applications like programming s. Commonly, terminal symbols are denoted using lowercase letters (such as aa, bb) for abstract alphabets or quoted strings (such as "if" or "while") for concrete tokens in syntactic grammars. The concept of terminal symbols was introduced by Noam Chomsky in his 1956 paper "Three Models for the Description of Language," where they were defined as part of the terminal vocabulary VTV_T in phrase-structure grammars, representing the observable primitives of linguistic output. This foundational distinction enabled the formal analysis of language generation and influenced subsequent developments in automata theory and compiler design.

Nonterminal symbols

In formal grammars, nonterminal symbols, also known as variables or auxiliary symbols, are placeholders that can be expanded or replaced according to production rules to derive sequences of other symbols, eventually leading to terminal symbols that form the strings of the language. These symbols belong to a disjoint from the terminal and serve as intermediate elements in the generative process of the grammar. Nonterminal symbols represent syntactic categories, such as (NP) or (VP), and correspond to the internal nodes in derivation trees, where each nonterminal expands into its productions to build the hierarchical structure of sentences. The start symbol, typically denoted as S, is a distinguished nonterminal from which all derivations begin, ensuring a unique entry point for generating strings. For a grammar to be well-defined, the set of nonterminals must be finite, allowing for a complete and recursive specification of the without . Common notation for nonterminal symbols includes uppercase letters, such as S, A, or B, to distinguish them from lowercase terminal symbols. In extended notations like Backus-Naur Form (BNF), nonterminals are often enclosed in angle brackets, as in for an expression category, facilitating readability in descriptions of programming languages or syntax. Unlike terminal symbols, which are the fixed atomic units that appear in the final output strings of the language, nonterminals are replaceable and do not occur in any generated sentence, serving solely as structural scaffolding during derivation.

Grammar Integration

Production rules

In formal language theory, a production rule specifies a directed replacement operation that transforms a nonterminal symbol into a sequence of terminal and nonterminal symbols, serving as the core mechanism for generating strings in a . Formally, such a rule takes the form A→αA \to \alpha, where AA is a single nonterminal symbol and α\alpha is a (possibly empty) string composed of zero or more symbols from the terminal and nonterminal alphabets. The left-hand side (LHS) of a production rule consists exclusively of a single nonterminal symbol, ensuring the replacement targets a specific . In contrast, the right-hand side (RHS) may include any combination of terminal symbols (which cannot be further expanded), nonterminal symbols (which can be replaced by other rules), or the ϵ\epsilon, allowing for flexible of linguistic structures. Production rules vary by grammar type within the , with context-free grammars (Type-2) featuring the simplest form where the LHS is a single nonterminal and the RHS is unrestricted in length, making them the primary focus for many applications in syntax analysis. Context-sensitive grammars (Type-1), by comparison, permit a more complex LHS of the form α1Aα2→α1ωα2\alpha_1 A \alpha_2 \to \alpha_1 \omega \alpha_2, where α1\alpha_1 and α2\alpha_2 provide contextual constraints around the nonterminal AA, and ∣ω∣≥1|\omega| \geq 1 to ensure non-contraction, though these are less commonly used due to increased . A formal grammar GG is defined as the 4-tuple G=(N,T,P,S)G = (N, T, P, S), where NN is the of nonterminal symbols, TT is the of terminal symbols (with N∩T=∅N \cap T = \emptyset), PP is the of production rules, and S∈NS \in N is the distinguished start symbol from which derivations begin. This structure encapsulates how symbols integrate into rules to enumerate the language L(G)={w∈T∗∣S⇒∗w}L(G) = \{ w \in T^* \mid S \Rightarrow^* w \}, with the arrow ⇒\Rightarrow denoting a single application of a production. Grammars impose key constraints to maintain formal rigor: the set PP must be finite, preventing unbounded rule proliferation, while recursive rules—where a nonterminal appears in its own RHS—are permitted to capture hierarchical structures, provided they do not induce infinite derivations that render membership undecidable in higher types.

Symbol roles in derivations

In the derivation process of a , the generation of s begins with the start symbol, a designated nonterminal from which production rules are applied sequentially to replace nonterminals until a complete terminal is obtained. This process can follow a leftmost derivation strategy, where the leftmost nonterminal in the current is selected for replacement, or a rightmost derivation, where the rightmost nonterminal is chosen, both leading to the same but potentially through different sequences of steps. Nonterminal symbols play an active role in derivations by serving as placeholders that are systematically replaced according to production rules, facilitating the expansion of the structure toward the final output. In contrast, terminal symbols, once introduced into the string, remain fixed and unaltered throughout the process, accumulating to form the yield—the terminal string that constitutes a valid member of the grammar's language. Production rules act as the mechanism for these replacements, transforming nonterminals into mixtures of terminals and further nonterminals. During derivation, intermediate results are known as sentential forms, which are strings composed of both terminal and nonterminal symbols reflecting the partial progress of the generation. For instance, a sentential form might evolve as S⇒AB⇒aB⇒abS \Rightarrow AB \Rightarrow aB \Rightarrow ab, where each step substitutes a nonterminal until none remain. These forms illustrate the interplay between the two symbol types, with nonterminals driving the expansion and terminals building the unchanging core of the output. A derivation concludes upon termination, which occurs when the sentential form consists solely of terminal symbols, producing a in the language L(G)L(G) generated by the . Notably, some grammars permit multiple distinct derivations to yield the same terminal , indicating potential in the generation process.

Practical Illustrations

Basic example grammar

A simple yet illustrative example of a (CFG) that demonstrates the roles of terminal and nonterminal symbols is one generating the language of balanced parentheses strings. This grammar, often used in introductory formal language theory, is defined as G=(VN,VT,P,S)G = (V_N, V_T, P, S), where VN={S}V_N = \{S\} is the set of nonterminals with SS as the start symbol, VT={(,)}V_T = \{(, )\} is the set of terminals, and PP is the set of production rules: S→(S) ∣ SS ∣ εS \to (S) \ | \ SS \ | \ \varepsilon. In this grammar, the nonterminal SS serves as the start symbol and recurses to build nested structures, while the terminals (( and )) form the actual symbols output in the strings. The empty production S→εS \to \varepsilon allows for the empty string as a valid balanced case, representing zero open-close pairs. This setup highlights how nonterminals expand via rules to yield terminal strings, with no other nonterminals involved, keeping the grammar minimal. The generated by this grammar, L(G)L(G), consists of all well-formed strings of balanced parentheses, such as ε\varepsilon (empty), ()(), (())(()), ()()()(), and ((()))((())), but excludes unbalanced ones like (()(() or )(())((). Representative examples include single pairs like ()(), concatenated pairs like ()()()(), and nested ones like ((()))((())), all ensuring equal numbers of opening and closing parentheses with proper matching. This grammar exemplifies a minimal viable CFG by incorporating through the rule S→(S)S \to (S) for nesting and via S→[SS](/page/.ss)S \to [SS](/page/.ss) for sequencing, enabling the generation of arbitrarily complex balanced structures from basic symbols. It provides a foundation for understanding derivations, where repeated applications of rules transform the start symbol into terminal strings.

Step-by-step derivation

To illustrate the process of derivation in a , consider generating the string "()()" using the basic example grammar for balanced parentheses. A leftmost derivation proceeds by replacing the leftmost nonterminal symbol at each step. Starting from the start symbol SS, one possible sequence is: S⇒SS⇒(S)S⇒()S⇒()(S)⇒()()S \Rightarrow SS \Rightarrow (S)S \Rightarrow ()S \Rightarrow ()(S) \Rightarrow ()() This applies the productions S→SSS \to SS, then S→(S)S \to (S) to the left SS, then S→εS \to \varepsilon (replacing SS with the ), followed by S→(S)S \to (S) to the remaining SS, and finally S→εS \to \varepsilon again. Derivations can follow different orders; for instance, a rightmost derivation replaces the rightmost nonterminal first, yielding an alternative sequence for the same string: S⇒SS⇒S(S)⇒S()⇒(S)()⇒()()S \Rightarrow SS \Rightarrow S(S) \Rightarrow S() \Rightarrow (S)() \Rightarrow ()() Both approaches use the same productions but differ in selection order, demonstrating how multiple paths can lead to the same result in an ambiguous grammar. The yield of the derivation—the concatenation of all terminal symbols in the final sentential form, omitting any ε\varepsilon—is the string "()()", confirming that this word belongs to the language L(G)L(G) generated by the grammar. This derivation corresponds to a (or derivation tree) with SS as the root node. The root applies S→SSS \to SS, producing two child nodes each labeled SS. The left child SS applies S→(S)S \to (S), branching to leaves labeled '(', SS, and ')' in sequence, where the inner SS applies S→εS \to \varepsilon (a node labeled ε\varepsilon). The right child SS mirrors this structure. The frontier of the tree (leaves from left to right, excluding ε\varepsilon) yields "()()".

Broader Contexts

Applications in formal languages

Terminal and nonterminal symbols form the foundational elements of the , which classifies formal grammars and the languages they generate into four types based on expressive power. Type 2 grammars, known as context-free grammars (CFGs), rely on a start symbol and production rules where the left-hand side is a single nonterminal, and the right-hand side consists of terminals, nonterminals, or the . These grammars are pivotal for modeling the of programming languages, where terminals represent lexical tokens like keywords and operators, and nonterminals capture syntactic categories such as expressions or statements. Similarly, CFGs underpin analyses of , enabling the representation of hierarchical structures like phrases and phrases through recursive applications of nonterminals. In language recognition and , terminal symbols serve as the atomic units of input, such as keywords or identifiers, while nonterminals function as intermediate nodes in parse trees that organize these terminals into valid . During compilation, parsers process sequences of terminals produced by lexical analyzers and construct parse trees where nonterminal expansions reflect the grammar's production rules, facilitating semantic analysis and code generation. This approach ensures efficient recognition of context-free languages, as seen in tools like or that generate parsers from CFG specifications. Across language classes in the , the role of nonterminals varies by type. Type 3 grammars, corresponding to regular languages, impose stricter constraints, allowing only a single nonterminal on the left-hand side and at most one nonterminal on the right-hand side (preceded or followed by terminals), which limits their use to simpler patterns like finite automata states without deep nesting. In contrast, more expressive classes like context-free languages require in nonterminals to generate nested or balanced structures, such as parentheses or recursive function calls, enabling the modeling of inherently hierarchical phenomena. Practical applications extend to structured , where terminal and nonterminal symbols ensure syntactic validity. XML validation, for instance, leverages context-free grammars derived from Document Type Definitions (DTDs), treating XML tags and attributes as terminals and content models as nonterminal expansions to verify document structure. Likewise, SQL query parsing employs CFGs to analyze statements, with terminals as keywords like SELECT or WHERE, and nonterminals representing clauses or expressions, supporting database query optimization and execution.

Variations across grammar types

In the Chomsky hierarchy, the roles and constraints on terminal and nonterminal symbols vary significantly across grammar types, reflecting increasing restrictions on production rules that influence the generative capacity of each class. Type-3 grammars, known as regular grammars, impose the strictest limitations on nonterminals, restricting productions to forms such as A→aA \to a or A→aBA \to aB, where AA and BB are nonterminals and aa is a terminal; this linear structure emphasizes right-linear or left-linear patterns, with nonterminals serving primarily as state transitions in finite automata equivalents. Terminals here form the basic lexicon, appearing only on the right-hand side without further expansion. Type-2 grammars, or context-free grammars, relax these constraints by allowing productions of the form A→αA \to \alpha, where AA is a nonterminal and α\alpha is any string of terminals and nonterminals; this balanced use enables hierarchical structures like those in programming languages, with nonterminals representing syntactic categories that expand independently of surrounding context. Terminals remain the irreducible units that terminate derivations, ensuring the generated strings consist solely of them in the end. Type-1 grammars, classified as context-sensitive, extend expressiveness by permitting productions αAβ→αγβ\alpha A \beta \to \alpha \gamma \beta, where AA is a nonterminal, α\alpha and β\beta are arbitrary strings, and ∣γ∣≥1|\gamma| \geq 1; nonterminals thus operate within specific contexts, allowing dependencies that capture more complex linguistic phenomena, while the length-non-decreasing condition prevents contractions. Terminals function as before, as final symbols, but their insertion is governed by contextual expansions of nonterminals. Type-0 grammars, or unrestricted grammars, impose no form restrictions on productions, allowing arbitrary rewritings α→β\alpha \to \beta involving terminals and nonterminals; this maximal freedom treats symbols in general rewriting systems akin to Turing machines, where nonterminals can be replaced in any manner without contextual or length constraints. Across these types, terminals consistently serve as the final, non-rewritable symbols in derived strings, providing the alphabet for the language; however, the expandability and contextual dependencies of nonterminals progressively restrict from Type 0 to Type 3, delineating the hierarchy's power in modeling formal languages.

References

  1. https://web.stanford.edu/class/archive/cs/cs143/cs143.1128/handouts/080%20Formal%20Grammars.pdf
  2. http://homepage.cs.uiowa.edu/~jones/compiler/fall14/notes/09.shtml
  3. https://www.cse.psu.edu/~deh25/cmpsc461/notes/Syntax-Semantics-1.html
  4. https://www.geeksforgeeks.org/theory-of-computation/chomsky-hierarchy-in-theory-of-computation/
  5. https://chomsky.info/wp-content/uploads/195609-.pdf
  6. https://www.cs.odu.edu/~zeil/cs390/latest/Public/cfg/index.html
  7. https://somr.info/lib/Chomsky_1959.pdf
  8. https://www.cs.unc.edu/~plaisted/comp455/slides/pt3.2.pdf
  9. https://zoo.cs.yale.edu/classes/cs201/topics/topic-cfls.pdf
  10. https://ieeexplore.ieee.org/document/1056813
  11. https://www.cs.cmu.edu/~janh/courses/411/24/lectures/08-parsing.pdf
  12. https://pages.cs.wisc.edu/~fischer/cs536.f13/lectures/Lecture17.4up.pdf
  13. https://courses.cs.washington.edu/courses/cse311/20sp/doc/lecture21.pdf
  14. https://mrce.in/ebooks/Automata%20Theory%2C%20Languages%2C%20&%20Computation%20Introduction%203rd%20Ed.pdf
  15. https://cs.uwaterloo.ca/~mdtpetri/cs241/09-CFG.pdf
  16. https://courses.grainger.illinois.edu/cs374/fa2016/slides/07-CFG.pdf
  17. https://www.cs.rochester.edu/u/nelson/courses/csc_173/grammars/cfg.html
  18. https://faculty.sist.shanghaitech.edu.cn/faculty/songfu/cav/Dragon-book.pdf
  19. https://tallinzen.net/media/readings/chomsky_syntactic_structures.pdf
  20. https://web.stanford.edu/~jurafsky/slp3/old_feb24/17.pdf
  21. https://www.cs.cornell.edu/courses/cs2112/2021fa/lectures/parsing/
  22. https://www.cs.rochester.edu/u/scott/courses/173/notes/05_grammars
  23. http://welf.se/files/LNG02.pdf
  24. https://www.cs.cmu.edu/~janh/courses/411/23/lec/09-parsing.pdf
Add your contribution
Related Hubs
User Avatar
No comments yet.