Blossom algorithm

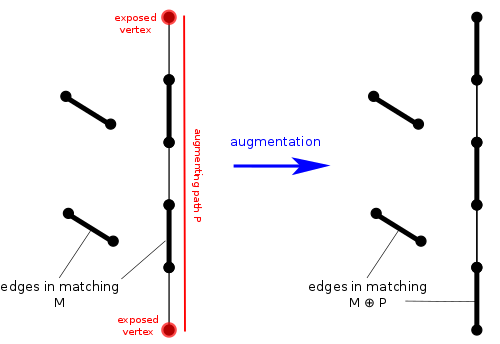
Given G = (V, E) and a matching M of G, a vertex v is exposed if no edge of M is incident with v. A path in G is an alternating path, if its edges are alternately not in M and in M (or in M and not in M). An augmenting path P is an alternating path that starts and ends at two distinct exposed vertices. Note that the number of unmatched edges in an augmenting path is greater by one than the number of matched edges, and hence the total number of edges in an augmenting path is odd. A matching augmentation along an augmenting path P is the operation of replacing M with a new matching

${\displaystyle M_{1}=M\oplus P=(M\setminus P)\cup (P\setminus M)}$.

By Berge's lemma, matching M is maximum if and only if there is no M-augmenting path in G.^[6][7] Hence, either a matching is maximum, or it can be augmented. Thus, starting from an initial matching, we can compute a maximum matching by augmenting the current matching with augmenting paths as long as we can find them, and return whenever no augmenting paths are left. We can formalize the algorithm as follows:

   INPUT:  Graph G, initial matching M on G
   OUTPUT: maximum matching M* on G
A1 function find_maximum_matching(G, M) : M*
A2     P ← find_augmenting_path(G, M)
A3     if P is non-empty then
A4         return find_maximum_matching(G, augment M along P)
A5     else
A6         return M
A7     end if
A8 end function

We still have to describe how augmenting paths can be found efficiently. The subroutine to find them uses blossoms and contractions.

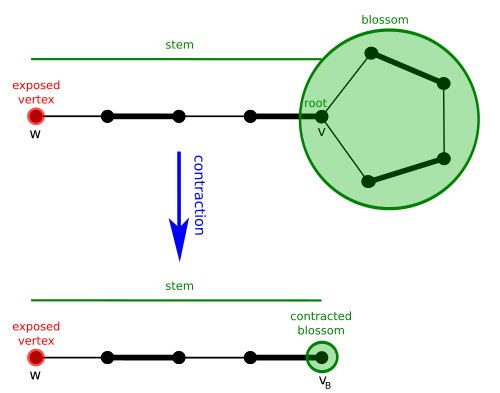
Given G = (V, E) and a matching M of G, a blossom B is a cycle in G consisting of 2k + 1 edges of which exactly k belong to M, and where one of the vertices v of the cycle (the base) is such that there exists an alternating path of even length (the stem) from v to an exposed vertex w.

Finding Blossoms:

• Traverse the graph starting from an exposed vertex.
• Starting from that vertex, label it as an outer vertex o.
• Alternate the labeling between vertices being inner i and outer o such that no two adjacent vertices have the same label.
• If we end up with two adjacent vertices labeled as outer o then we have an odd-length cycle and hence a blossom.

Define the contracted graph G' as the graph obtained from G by contracting every edge of B, and define the contracted matching M' as the matching of G' corresponding to M.

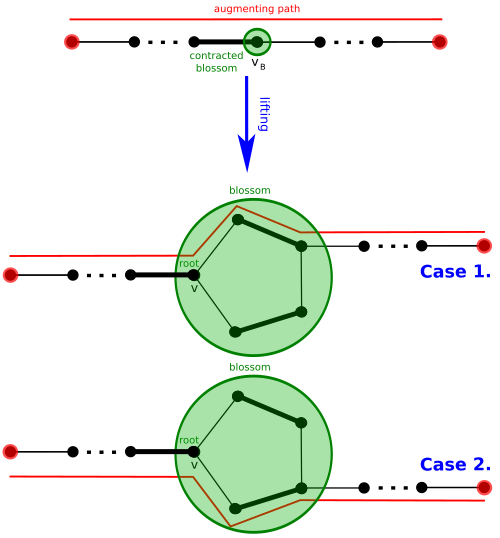
G' has an M'-augmenting path if and only if G has an M-augmenting path, and that any M'-augmenting path P' in G' can be lifted to an M-augmenting path in G by undoing the contraction by B so that the segment of P' (if any) traversing through v_B is replaced by an appropriate segment traversing through B.^[8] In more detail:

• if P' traverses through a segment u → v_B → w in G', then this segment is replaced with the segment u → ( u' → … → w' ) → w in G, where blossom vertices u' and w' and the side of B, ( u' → … → w' ), going from u' to w' are chosen to ensure that the new path is still alternating (u' is exposed with respect to ${\displaystyle M\cap B}$, ${\displaystyle \{w',w\}\in E\setminus M}$).

• if P' has an endpoint v_B, then the path segment u → v_B in G' is replaced with the segment u → ( u' → … → v' ) in G, where blossom vertices u' and v' and the side of B, ( u' → … → v' ), going from u' to v' are chosen to ensure that the path is alternating (v' is exposed, ${\displaystyle \{u',u\}\in E\setminus M}$).

Thus blossoms can be contracted and search performed in the contracted graphs. This reduction is at the heart of Edmonds' algorithm.

The search for an augmenting path uses an auxiliary data structure consisting of a forest F whose individual trees correspond to specific portions of the graph G. In fact, the forest F is the same that would be used to find maximum matchings in bipartite graphs (without need for shrinking blossoms). In each iteration the algorithm either (1) finds an augmenting path, (2) finds a blossom and recurses onto the corresponding contracted graph, or (3) concludes there are no augmenting paths. The auxiliary structure is built by an incremental procedure discussed next.^[8]

The construction procedure considers vertices v and edges e in G and incrementally updates F as appropriate. If v is in a tree T of the forest, we let root(v) denote the root of T. If both u and v are in the same tree T in F, we let distance(u,v) denote the length of the unique path from u to v in T.

    INPUT:  Graph G, matching M on G
    OUTPUT: augmenting path P in G or empty path if none found
B01 function find_augmenting_path(G, M) : P
B02    F ← empty forest
B03    unmark all vertices and edges in G, mark all edges of M
B05    for each exposed vertex v do
B06        create a singleton tree { v } and add the tree to F
B07    end for
B08    while there is an unmarked vertex v in F with distance(v, root(v)) even do
B09        while there exists an unmarked edge e = { v, w } do
B10            if w is not in F then
                   // w is matched, so add e and w's matched edge to F
B11                x ← vertex matched to w in M
B12                add edges { v, w } and { w, x } to the tree of v
B13            else
B14                if distance(w, root(w)) is odd then
                       // Do nothing.
B15                else
B16                    if root(v) ≠ root(w) then
                           // Report an augmenting path in F ${\displaystyle \cup }$ { e }.
B17                        P ← path (root(v) → ... → v) → (w → ... → root(w))
B18                        return P
B19                    else
                           // Contract a blossom in G and look for the path in the contracted graph.
B20                        B ← blossom formed by e and edges on the path v → w in T
B21                        G’, M’ ← contract G and M by B
B22                        P’ ← find_augmenting_path(G’, M’)
B23                        P ← lift P’ to G
B24                        return P
B25                    end if
B26                end if
B27            end if
B28            mark edge e
B29        end while
B30        mark vertex v
B31    end while
B32    return empty path
B33 end function

The following four figures illustrate the execution of the algorithm. Dashed lines indicate edges that are currently not present in the forest. First, the algorithm processes an out-of-forest edge that causes the expansion of the current forest (lines B10 – B12).

Next, it detects a blossom and contracts the graph (lines B20 – B21).

Finally, it locates an augmenting path P′ in the contracted graph (line B22) and lifts it to the original graph (line B23). Note that the ability of the algorithm to contract blossoms is crucial here; the algorithm cannot find P in the original graph directly because only out-of-forest edges between vertices at even distances from the roots are considered on line B17 of the algorithm.

The forest F constructed by the find_augmenting_path() function is an alternating forest.^[9]

• a tree T in G is an alternating tree with respect to M, if
  • T contains exactly one exposed vertex r called the tree root
  • every vertex at an odd distance from the root has exactly two incident edges in T, and
  • all paths from r to leaves in T have even lengths, their odd edges are not in M and their even edges are in M.
• a forest F in G is an alternating forest with respect to M, if
  • its connected components are alternating trees, and
  • every exposed vertex in G is a root of an alternating tree in F.

Each iteration of the loop starting at line B09 either adds to a tree T in F (line B10) or finds an augmenting path (line B17) or finds a blossom (line B20). It is easy to see that the running time is ${\displaystyle O(|E||V|^{2})}$.

When G is bipartite, there are no odd cycles in G. In that case, blossoms will never be found and one can simply remove lines B20 – B24 of the algorithm. The algorithm thus reduces to the standard algorithm to construct maximum cardinality matchings in bipartite graphs^[7] where we repeatedly search for an augmenting path by a simple graph traversal: this is for instance the case of the Ford–Fulkerson algorithm.

The matching problem can be generalized by assigning weights to edges in G and asking for a set M that produces a matching of maximum (minimum) total weight: this is the maximum weight matching problem. This problem can be solved by a combinatorial algorithm that uses the unweighted Edmonds's algorithm as a subroutine.^[6] Vladimir Kolmogorov provides an efficient C++ implementation of this.^[10]