Hubbry Logo
RIPEMDRIPEMDMain
Open search
RIPEMD
Community hub
RIPEMD
logo
8 pages, 0 posts
0 subscribers
Be the first to start a discussion here.
Be the first to start a discussion here.
Contribute something
RIPEMD
RIPEMD
RIPEMD
View on Wikipedia
from Wikipedia
RIPEMD
General
DesignersHans Dobbertin, Antoon Bosselaers and Bart Preneel
First published1992
CertificationRIPEMD-160: CRYPTREC (Monitored)
Detail
Digest sizes128, 160, 256, 320 bits
A sub-block from the compression function of the RIPEMD-160 hash algorithm
Wikifunctions has an RIPEMD-128 function.
Wikifunctions has an RIPEMD-160 function.

RIPEMD (RIPE Message Digest) is a family of cryptographic hash functions developed in 1992 (the original RIPEMD) and 1996 (other variants). There are five functions in the family: RIPEMD, RIPEMD-128, RIPEMD-160, RIPEMD-256, and RIPEMD-320, of which RIPEMD-160 is the most common.[citation needed]

The original RIPEMD, as well as RIPEMD-128, is not considered secure because 128-bit result is too small and also (for the original RIPEMD) because of design weaknesses. The 256- and 320-bit versions of RIPEMD provide the same level of security as RIPEMD-128 and RIPEMD-160, respectively; they are designed for applications where the security level is sufficient but longer hash result is necessary.

While RIPEMD functions are less popular than SHA-1 and SHA-2, they are used, among others, in Bitcoin and other cryptocurrencies based on Bitcoin.[1]

History

[edit]

The original RIPEMD function was designed in the framework of the EU project RIPE (RACE Integrity Primitives Evaluation) in 1992.[2][3] Its design was based on the MD4 hash function. In 1996, in response to security weaknesses found in the original RIPEMD,[4] Hans Dobbertin, Antoon Bosselaers and Bart Preneel at the COSIC research group at the Katholieke Universiteit Leuven in Leuven, Belgium published four strengthened variants: RIPEMD-128, RIPEMD-160, RIPEMD-256, and RIPEMD-320.[5]

In August 2004, a collision was reported for the original RIPEMD.[6] This does not apply to RIPEMD-160.[7]

In 2019, the best collision attack for RIPEMD-160 could reach 34 rounds out of 80 rounds, which was published at CRYPTO 2019.[8]

In February 2023, a collision attack for RIPEMD-160 was published at EUROCRYPT 2023, which could reach 36 rounds out of 80 rounds with time complexity of 264.5.[9]

In December 2023, an improved collision attack was found based on the technique from the previous best collision attack, this improved collision attack could reach 40 rounds out of 80 round with a theoretical time complexity of 249.9.[10]

RIPEMD-160 hashes

[edit]

The 160-bit RIPEMD-160 hashes (also termed RIPE message digests) are typically represented as 40-digit hexadecimal numbers. The following demonstrates a 43-byte ASCII input and the corresponding RIPEMD-160 hash: 

 RIPEMD-160("The quick brown fox jumps over the lazy dog") =
 37f332f68db77bd9d7edd4969571ad671cf9dd3b

RIPEMD-160 behaves with the desired avalanche effect of cryptographic hash functions (small changes, e.g. changing d to c, result in a completely different hash): 

 RIPEMD-160("The quick brown fox jumps over the lazy cog") =
 132072df690933835eb8b6ad0b77e7b6f14acad7

The hash of a zero-length string is: 

 RIPEMD-160("") =
 9c1185a5c5e9fc54612808977ee8f548b2258d31

Implementations

[edit]

Below is a list of cryptography libraries that support RIPEMD (specifically RIPEMD-160):

See also

[edit]

References

[edit]
[edit]
Revisions and contributorsEdit on WikipediaRead on Wikipedia

RIPEMD

View on Grokipedia
from Grokipedia
RIPEMD (RACE Integrity Primitives Evaluation Message Digest) is a family of cryptographic s designed for applications such as digital signatures, message , and verification. Developed by Hans Dobbertin, Antoon Bosselaers, and Preneel as part of the European Union's RACE Integrity Primitives Evaluation (RIPE) project (1988–1992), the original RIPEMD was introduced in 1992 as a 128-bit hash function inspired by the , aiming to provide secure message digests on 32-bit processors. In 1996, due to emerging cryptanalytic weaknesses in the original design and related functions like and , the team published RIPEMD-160 as a strengthened variant. This iteration produces a 160-bit hash value, incorporates five rounds of processing (up from three in the original), and employs two parallel computation lines with distinct Boolean functions, rotations, and message word permutations to enhance and overall security. RIPEMD-160 was explicitly intended as a more secure replacement for 128-bit hashes like and the initial RIPEMD, with design choices tuned for efficient software implementation on 32-bit architectures. The RIPEMD family was later expanded to include additional variants: RIPEMD-128 (a direct 128-bit successor to the original), RIPEMD-256 (producing 256 bits), and RIPEMD-320 (producing 320 bits), each maintaining the core parallel structure while adjusting output lengths for varying security needs. While the original RIPEMD and RIPEMD-128 are no longer recommended due to identified vulnerabilities, RIPEMD-160 remains considered secure against practical attacks as of 2025, though theoretical advances in continue; it has been largely supplanted by the family in modern standards. RIPEMD-160 is specified in the original design document and included in the ISO/IEC 10118-3:2018 standard on dedicated hash-functions, and it has found niche use in legacy systems, certain protocols requiring lightweight hashing, and notably in the for generating addresses from public keys.

Overview

Definition and Purpose

RIPEMD is a family of cryptographic hash functions designed to produce a fixed-size output, typically 128 to 320 bits, from messages of arbitrary length, serving as one-way functions for secure message digestion. These functions map input data to a compact digest that uniquely represents the original message without allowing easy reversal. The primary purpose of RIPEMD in is to ensure by detecting unauthorized modifications, support message authentication through verifiable digests, and enable digital signatures by providing a secure basis for signing fixed-length values. It resists key attacks including preimage (finding an input for a given output), second-preimage (finding a different input for the same output), and collision (finding two inputs with the same output) attacks, with levels scaling to the output size, such as approximately 2^80 operations for collisions in 160-bit variants. Key design goals for the RIPEMD family include providing a European-developed alternative to the and hash functions, with an emphasis on strong and the , where even a single-bit change in the input produces a significantly different output (at least 50% bit flips on average). The functions are deterministic, computationally efficient for software implementation on 32-bit processors, and maintain these properties across variants, with RIPEMD-160 being the most widely adopted for its balanced security and performance.

Family of Variants

The RIPEMD family encompasses several cryptographic hash functions designed primarily for message authentication and integrity verification, evolving from the original proposal to address emerging security needs. The original RIPEMD, introduced in 1992, produces a 128-bit output with an internal state of 128 bits (four 32-bit words), utilizing two parallel branches inspired by MD4 to enhance collision resistance. In 1996, strengthened variants were developed to mitigate identified weaknesses in the original design, including a plug-in replacement RIPEMD-128 with a 128-bit output and 128-bit internal state (four 32-bit words), and RIPEMD-160 with a 160-bit output and 160-bit internal state (five 32-bit words). These updates incorporated refinements such as increased round counts and differentiated operations between branches. The family further includes RIPEMD-256 and RIPEMD-320, both proposed in 1996 as double-length extensions of RIPEMD-128 and RIPEMD-160, respectively, yielding 256-bit and 320-bit outputs with corresponding internal states of 256 bits and 320 bits to support applications requiring longer digests. These variants were created to bolster security margins against brute-force attacks, where larger output sizes exponentially increase the effort required for preimage or collision searches, while maintaining compatibility with the core double-branch architecture.
VariantOutput Size (bits)Internal State Size (bits)Publication YearPrimary Design Improvements
Original RIPEMD1281281992Parallel MD4-like branches with varied shifts and constants
RIPEMD-1281281281996Plug-in strengthening with four rounds and refined message ordering
RIPEMD-1601601601996Five rounds, enhanced branch differences, and rotation mechanisms for added
RIPEMD-2562562561996Double-length extension of RIPEMD-128 with register swapping for inter-branch interaction
RIPEMD-3203203201996Double-length extension of RIPEMD-160 with register swapping for inter-branch interaction

History

Development in the RIPE Project

The RIPE (RACE Integrity Primitives Evaluation) project was an initiative funded by the European Commission's RACE (Research and Development in Advanced Communications Technologies in ) program, running from 1988 to 1992, with the primary goal of developing a suite of cryptographic integrity primitives suitable for open networks, particularly the emerging Integrated Broadband Communication (IBC) systems. This effort focused on creating secure mechanisms for , message , and related functions, excluding confidentiality primitives, to foster and in pan-European . The consortium involved academic and industrial partners, including Katholieke Universiteit (KU ), which played a central role in the design of hash functions. Within this framework, the original RIPEMD (RIPE Message Digest) emerged as a key output, designed by Antoon Bosselaers and Bart Preneel at . Hans Dobbertin later contributed to its and the development of strengthened variants. Proposed in 1992 as RIPEMD-0, it was structured as an enhanced variant of Ronald Rivest's algorithm, incorporating a 128-bit output length to provide robust for practical applications. The design emphasized software efficiency on 32-bit processors while addressing early vulnerabilities identified in MD4 through structural modifications, such as parallel processing lines. The project's motivations were driven by concerns over the of U.S.-developed hash functions like and the subsequent , which had shown susceptibility to partial attacks, prompting a need for independent European alternatives. RIPEMD was thus positioned as a for primitives, aiming to support secure information systems in distributed environments without relying on designs. This initial version laid the groundwork for subsequent refinements within the RIPEMD family.

Evolution of Variants

Following the initial development of RIPEMD in 1992 as part of the European RACE Integrity Primitives Evaluation (RIPE) project, significant weaknesses were identified in its design by early 1995, prompting major revisions. Specifically, cryptanalyst Hans Dobbertin demonstrated collisions in the last two rounds of the original RIPEMD, exploiting similarities to the vulnerable . In response, Dobbertin, along with Antoon Bosselaers and Bart Preneel, introduced strengthened variants in 1996: RIPEMD-128, which retained a 128-bit output but added an extra round for improved resistance, and RIPEMD-160, which extended the output to 160 bits with five rounds total. These revisions addressed the original's insufficient security margin against brute-force attacks, where a 128-bit hash could theoretically be collided in days using specialized hardware costing around $10 million. A key evolutionary refinement in RIPEMD-160 was the enhancement of its parallel branch structure for superior of changes across the message digest. Unlike the original RIPEMD's more uniform parallel MD4-like branches, RIPEMD-160 incorporated distinct functions, shifted message word orders, and periodic exchanges of variables between branches every round, making differential attacks significantly harder. This design directly countered the early collision findings while maintaining compatibility with 32-bit processors for efficient implementation. RIPEMD-160 quickly gained traction as a secure alternative to , influencing subsequent European cryptographic efforts by providing a model for parallel-branch hashes resistant to known MD-family vulnerabilities. To accommodate emerging needs for longer hash outputs without proportionally increasing computational security requirements, RIPEMD-256 and RIPEMD-320 were introduced as double-length extensions of RIPEMD-128 and RIPEMD-160, respectively, in the same 1996 framework. These variants apply the core compression function twice per block, with register swapping between iterations to ensure avalanche effects, targeting applications like digital signatures where 256- or 320-bit digests enhance for larger key spaces. Standardization efforts solidified the family's role in international . RIPEMD-160 and RIPEMD-128 were formally adopted in the ISO/IEC 10118-3 standard for dedicated hash functions in 2004, with revisions in 2018 confirming their specifications and s for . RIPEMD-256 received an from TeleTrusT. This timeline reflected growing recognition of RIPEMD's contributions to secure hash design in , bridging the gap between prototypes and deployable standards.

Algorithm Design

General Structure

The RIPEMD family of cryptographic hash functions employs the Merkle-Damgård construction to process input messages securely. The overall process begins with the input message to a length that is a multiple of the 512-bit block size. This involves appending a single '1' bit, followed by sufficient '0' bits to reach 448 bits modulo 512, and concluding with a 64-bit little-endian representation of the original message length in bits. This ensures unambiguous recovery of the message length and prevents ambiguities in . The hashing iteration initializes a set of variables that maintain the intermediate state across blocks. Variants differ in state size: earlier ones like the original RIPEMD and RIPEMD-128 use four 32-bit words (A, B, C, D), while RIPEMD-160 and later use five (A, B, C, D, E). These are initialized to fixed constants derived from the fractional parts of the square roots of the first few prime numbers (√2, √3, etc.), scaled by 2322^{32} and taken as integers. For example, in RIPEMD-160:
  • h0 = 0x67452301 (from √2)
  • h1 = 0xefcdab89 (from √3)
  • h2 = 0x98badcfe (from √5)
  • h3 = 0x10325476 (from √7)
  • h4 = 0xc3d2e1f0 (from √11)
    RIPEMD-128 uses the first four of these. These "nothing-up-my-sleeve" constants provide a verifiable, non-arbitrary starting point to enhance trust in the .
Each padded 512-bit block is divided into 16 consecutive 32-bit words, denoted X0 to X15, processed in little-endian byte order. The block undergoes iterative compression by updating the chaining variables through a number of sequential steps grouped into rounds, varying by variant: 48 steps in three rounds for the original RIPEMD, 64 steps in four rounds for RIPEMD-128, and 80 steps in five rounds for RIPEMD-160. In each step, nonlinear functions, modular additions, left rotations, and constant additions are applied to the state words, incorporating message words in a specific nonlinear order unique to each round. This processing occurs in two parallel branches—a left branch mirroring an MD4-like structure and a right branch with modified operations—before the branches interact in the final steps to produce the updated variables for the next block. Key structural variations across the family include the number of rounds and functions used (three functions f1-f3 for original RIPEMD, four f1-f4 for RIPEMD-128, five f1-f5 for RIPEMD-160), message word permutations, and branch combination methods (e.g., RIPEMD-256 and RIPEMD-320 output both branches separately without final mixing for longer digests). Upon completing the compression for all blocks, the final chaining variables are concatenated in order to yield the hash digest. Depending on the variant, the output may be truncated to a specific length, such as 160 bits for RIPEMD-160 or 128 bits for RIPEMD-128.

Compression Function

The compression function in RIPEMD variants processes a 512-bit message block together with the current chaining variables (e.g., 128-bit for RIPEMD-128 or 160-bit for RIPEMD-160) to produce updated chaining variables of the same length, forming the core of the Merkle-Damgård construction used across the family. This mechanism iteratively compresses the input message by incorporating block data and prior state through a series of bitwise and arithmetic operations designed for . The number of rounds varies by variant, with each round consisting of 16 steps (e.g., five rounds for 80 steps in RIPEMD-160). Each round applies nonlinear functions operating on three 32-bit words x, y, z via bitwise operations to introduce nonlinearity. The functions differ by variant: earlier ones use f1 to f3 or f4; RIPEMD-160 uses five, denoted f1 to f5:
  • f1(x, y, z) = x ⊕ y ⊕ z
  • f2(x, y, z) = (x ∧ y) ∨ (¬x ∧ z)
  • f3(x, y, z) = (x ∨ ¬y) ⊕ z
  • f4(x, y, z) = (x ∧ z) ∨ (y ∧ ¬z)
  • f5(x, y, z) = x ⊕ (y ∨ ¬z)
These functions, inspired by but diversified for enhanced diffusion, are applied sequentially across rounds, with the left branch using them in forward order and the right branch in reverse (where applicable). In each step, the nonlinear function output is combined with a 32-bit word, a round-specific constant, and the current state value via modulo 232, followed by a left and another to update the state registers. Specifically, for a register A, the update is A ← ((A + f(B, C, D) + Xi + Kj) ≪ s) + E, where Xi is the word, Kj is the constant, s is the rotation amount (varying from 5 to 30 bits across steps), and registers cycle through the state. words are fed into the steps via permutations that differ between branches, ensuring thorough mixing. All variants employ two parallel branches—a left and a right line—each performing the independently on the same input but with distinct permutations, constants, and schedules to amplify against differential attacks. The branches are combined at the end by adding corresponding output registers pairwise modulo 232 (with selective final rotations on some registers in certain variants), yielding the new chaining variables that propagate to the next block. This dual-line design, present since the original RIPEMD but refined in later variants, distinguishes the family from single-branch functions like by promoting greater avalanche effects and resistance to linear approximations. For RIPEMD-256 and RIPEMD-320, the branches are not combined, allowing longer outputs.

RIPEMD-160

Specifications

RIPEMD-160 produces a 160-bit hash value, represented as five 32-bit words, serving as the output from the final state of the compression function. The algorithm initializes five 32-bit registers, denoted as A, B, C, D, and E, with the following hexadecimal constants:
A = 0x67452301
B = 0xEFCDAB89
C = 0x98BADCFE
D = 0x10325476
E = 0xC3D2E1F0
These values are the same as the initial chaining variables used in MD5. Message padding follows the MD4 convention: a single '1' bit is appended to the input message, followed by zero or more '0' bits to ensure the total length is congruent to 448 512 bits; then, the original message length in bits is appended as a 64-bit big-endian , making the padded message a multiple of 512 bits. The compression function employs 80 steps divided into five rounds, with distinct constants KjK_j for the left branch and Kj′K'_j for the right branch, applied across the steps j=0j = 0 to 7979. These constants are selected as fractional parts of the square roots of prime numbers, scaled and truncated to 32 bits, and vary by round as shown in the table below:
Step RangeLeft Constant KjK_j (hex)Right Constant Kj′K'_j (hex)
0–150x000000000x50A28BE6
16–310x5A8279990x5C4DD124
32–470x6ED9EBA10x6D703EF3
48–630x8F1BBCDC0x7A6D76E9
64–790xA953FD4E0x00000000
Left rotations are applied to intermediate values in each step, with amounts sjs_j for the left branch and sj′s'_j for the right branch, chosen to enhance and effects. The rotation schedules, grouped by round, are:
Step RangeLeft Rotations sjs_jRight Rotations sj′s'_j
0–1511,14,15,12,5,8,7,9,11,13,14,15,6,7,9,88,9,9,11,13,15,15,5,7,7,8,11,14,14,12,6
16–317,6,8,13,11,9,7,15,7,12,15,9,11,7,13,129,13,15,7,12,8,9,11,7,7,12,7,6,15,13,11
32–4711,13,6,7,14,9,13,15,14,8,13,6,5,12,7,59,7,15,11,8,6,6,14,12,13,5,14,13,13,7,5
48–6311,12,14,15,14,15,9,8,9,14,5,6,8,6,5,1215,5,8,11,14,14,6,14,6,9,12,9,12,5,15,8
64–799,15,5,11,6,8,13,12,5,12,13,14,11,8,5,68,5,12,9,12,5,14,6,8,13,6,5,15,13,11,11
The left branch processes five rounds using nonlinear functions in sequence: f1(j)=(Xj⊕Yj⊕Zj)f_1(j) = (X_j \oplus Y_j \oplus Z_j), f2(j)=(Xj∧Yj)∨(¬Xj∧Zj)f_2(j) = (X_j \land Y_j) \lor (\lnot X_j \land Z_j), f3(j)=(Xj∨¬Yj)⊕Zjf_3(j) = (X_j \lor \lnot Y_j) \oplus Z_j, f4(j)=(Xj∧Zj)∨(Yj∧¬Zj)f_4(j) = (X_j \land Z_j) \lor (Y_j \land \lnot Z_j), and f5(j)=Xj⊕(Yj∨¬Zj)f_5(j) = X_j \oplus (Y_j \lor \lnot Z_j), with message words selected in orders derived from identity, rotations ρ\rho, ρ2\rho^2, ρ3\rho^3, and ρ4\rho^4 permutations. The right branch mirrors this structure but applies the functions in reverse order (f5f_5 to f1f_1) and uses permuted message orders based on π\pi, ρπ\rho \pi, ρ2π\rho^2 \pi, ρ3π\rho^3 \pi, and ρ4π\rho^4 \pi, ensuring parallel computation with independent diffusion paths. The message word indices r(j)r(j) and r′(j)r'(j) for the left and right branches, respectively, are as follows:
Step RangeLeft Indices r(j)r(j)Right Indices r′(j)r'(j)
0–150,1,2,3,4,5,6,7,8,9,10,11,12,13,14,155,14,7,0,9,2,11,4,13,6,15,8,1,10,3,12
16–317,4,13,1,10,6,15,3,12,0,9,5,2,14,11,86,11,3,7,0,13,5,10,14,15,8,12,4,9,1,2
32–473,10,14,4,9,15,8,1,2,7,0,6,13,11,5,1215,5,1,3,7,14,6,9,11,8,12,2,10,0,4,13
48–631,9,11,10,0,8,12,4,13,3,7,15,14,5,6,28,6,4,1,3,11,15,0,5,12,2,13,9,7,10,14
64–794,0,5,9,7,12,2,10,14,1,3,8,11,6,15,1312,9,15,5,0,4,8,6,2,7,13,1,3,10,11,14

Step-by-Step Process

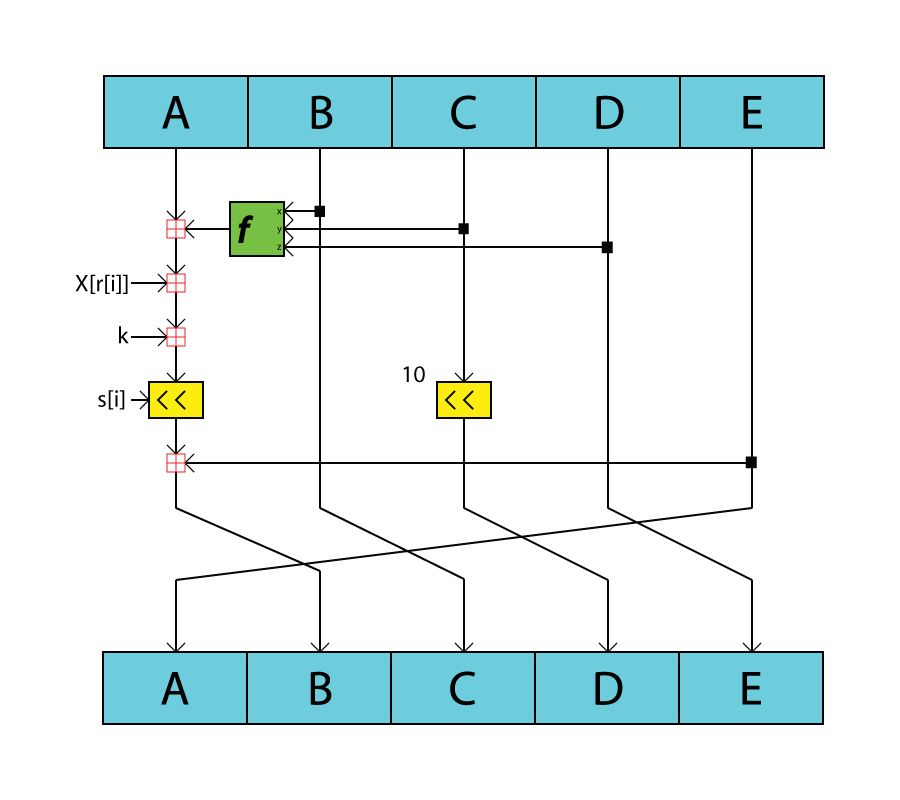
The preprocessing step in RIPEMD-160 pads the input message to ensure its length is a multiple of 512 bits, following the same method as MD4. Specifically, a single '1' bit (represented as the byte 0x80) is appended to the message, followed by zero or more '0' bits until the total length modulo 512 equals 448 bits. Then, the original message length in bits is appended as a 64-bit big-endian integer, resulting in a padded message divided into t blocks of 512 bits each, where each block comprises 16 32-bit words denoted X to X. For example, an empty message of 0 bits is padded by appending 0x80, followed by 55 zero bytes (440 zero bits), making the total length 448 bits, and then eight zero bytes for the length, forming a single 512-bit block. The computation begins by initializing five 32-bit chaining variables: h₀ = 0x67452301, h₁ = 0xEFCDAB89, h₂ = 0x98BADCFE, h₃ = 0x10325476, h₄ = 0xC3D2E1F0. For each 512-bit message block Xᵢ, these chaining variables are copied to two sets of working variables for parallel processing: the left line (A = h₀, B = h₁, C = h₂, D = h₃, E = h₄) and the right line (A' = h₀, B' = h₁, C' = h₂, D' = h₃, E' = h₄). Each line then performs 80 iterative steps, grouped into five rounds of 16 steps each (j = 0 to 79), where all operations are 2³². In each step j of the left line, a temporary value T is computed as
T=ρs(j)(A+fj(B,C,D)+Xr(j)+Kj)+E,T = \rho_{s(j)} \left( A + f_j(B, C, D) + X_{r(j)} + K_j \right) + E,
where ρs\rho_s denotes a left rotation by s bits, fjf_j is the round-dependent nonlinear function, r(j)r(j) selects the message word index, and KjK_j is the round constant; the working variables are then updated as A ← E, E ← D, D ← ρ10(C)\rho_{10}(C), C ← B, B ← T. The right line follows an analogous process but applies the nonlinear functions in reverse order (f5 to f1 across the five rounds):
T′=ρs′(j)(A′+f(79−j)(B′,C′,D′)+Xr′(j)+Kj′)+E′,T' = \rho_{s'(j)} \left( A' + f(79-j)(B', C', D') + X_{r'(j)} + K'_j \right) + E',
followed by A' ← E', E' ← D', D' ← ρ10(C′)\rho_{10}(C'), C' ← B', B' ← T', with distinct s′(j)s'(j), r′(j)r'(j), and Kj′K'_j. The nonlinear functions fjf_j, rotation amounts s(j)s(j) and s′(j)s'(j), message word orders r(j)r(j) and r′(j)r'(j), and constants KjK_j and Kj′K'_j are predefined per round as specified in the RIPEMD-160 parameters. After completing the 80 steps, the final working variables from both lines are combined to update the chaining variables as follows:
h₀ ← h₁ + C + D',
h₁ ← h₂ + D + E',
h₂ ← h₃ + E + A',
h₃ ← h₄ + A + B',
h₄ ← h₀ + B + C'. This updated 160-bit chaining value (concatenation of h₀ to h₄) is fed as input to the next block, and after all blocks are processed, it forms the final hash output. The following pseudocode outlines the compression function for a single 512-bit block:

procedure RIPEMD160_Compress(h0, h1, h2, h3, h4, X[0..15]) // Copy chaining vars to left and right lines A = h0; B = h1; C = h2; D = h3; E = h4 A_ = h0; B_ = h1; C_ = h2; D_ = h3; E_ = h4 // Right line with prime notation for j = 0 to 79 do // Left line step if j < 16 then f = B xor C xor D K = 0x00000000 s = s_left[j] r_idx = r_left[j] else if j < 32 then f = (B and C) or (not B and D) K = 0x5A827999 s = s_left[j] r_idx = r_left[j] else if j < 48 then f = (B or not C) xor D K = 0x6ED9EBA1 s = s_left[j] r_idx = r_left[j] else if j < 64 then f = (B and D) or (C and not D) K = 0x8F1BBCDC s = s_left[j] r_idx = r_left[j] else f = B xor (C or not D) K = 0xA953FD4E s = s_left[j] r_idx = r_left[j] T = rol_s(A + f + X[r_idx] + K) + E A = E; E = D; D = rol_10(C); C = B; B = T // Right line step (reversed rounds) if j < 16 then f_ = B_ xor (C_ or not D_) K_ = 0x50A28BE6 s_ = s_right[j] r_idx_ = r_right[j] else if j < 32 then f_ = (B_ and D_) or (C_ and not D_) K_ = 0x5C4DD124 s_ = s_right[j] r_idx_ = r_right[j] else if j < 48 then f_ = (B_ or not C_) xor D_ K_ = 0x6D703EF3 s_ = s_right[j] r_idx_ = r_right[j] else if j < 64 then f_ = (B_ and C_) or (not B_ and D_) K_ = 0x7A6D76E9 s_ = s_right[j] r_idx_ = r_right[j] else f_ = B_ xor C_ xor D_ K_ = 0x00000000 s_ = s_right[j] r_idx_ = r_right[j] T_ = rol_{s_}(A_ + f_ + X[r_idx_] + K_) + E_ A_ = E_; E_ = D_; D_ = rol_10(C_); C_ = B_; B_ = T_ // Finalization: Update chaining variables h0 = h1 + C + D_ h1 = h2 + D + E_ h2 = h3 + E + A_ h3 = h4 + A + B_ h4 = h0 + B + C_ return (h0, h1, h2, h3, h4)

procedure RIPEMD160_Compress(h0, h1, h2, h3, h4, X[0..15]) // Copy chaining vars to left and right lines A = h0; B = h1; C = h2; D = h3; E = h4 A_ = h0; B_ = h1; C_ = h2; D_ = h3; E_ = h4 // Right line with prime notation for j = 0 to 79 do // Left line step if j < 16 then f = B xor C xor D K = 0x00000000 s = s_left[j] r_idx = r_left[j] else if j < 32 then f = (B and C) or (not B and D) K = 0x5A827999 s = s_left[j] r_idx = r_left[j] else if j < 48 then f = (B or not C) xor D K = 0x6ED9EBA1 s = s_left[j] r_idx = r_left[j] else if j < 64 then f = (B and D) or (C and not D) K = 0x8F1BBCDC s = s_left[j] r_idx = r_left[j] else f = B xor (C or not D) K = 0xA953FD4E s = s_left[j] r_idx = r_left[j] T = rol_s(A + f + X[r_idx] + K) + E A = E; E = D; D = rol_10(C); C = B; B = T // Right line step (reversed rounds) if j < 16 then f_ = B_ xor (C_ or not D_) K_ = 0x50A28BE6 s_ = s_right[j] r_idx_ = r_right[j] else if j < 32 then f_ = (B_ and D_) or (C_ and not D_) K_ = 0x5C4DD124 s_ = s_right[j] r_idx_ = r_right[j] else if j < 48 then f_ = (B_ or not C_) xor D_ K_ = 0x6D703EF3 s_ = s_right[j] r_idx_ = r_right[j] else if j < 64 then f_ = (B_ and C_) or (not B_ and D_) K_ = 0x7A6D76E9 s_ = s_right[j] r_idx_ = r_right[j] else f_ = B_ xor C_ xor D_ K_ = 0x00000000 s_ = s_right[j] r_idx_ = r_right[j] T_ = rol_{s_}(A_ + f_ + X[r_idx_] + K_) + E_ A_ = E_; E_ = D_; D_ = rol_10(C_); C_ = B_; B_ = T_ // Finalization: Update chaining variables h0 = h1 + C + D_ h1 = h2 + D + E_ h2 = h3 + E + A_ h3 = h4 + A + B_ h4 = h0 + B + C_ return (h0, h1, h2, h3, h4)

(Note: The arrays s_left, r_left, s_right, and r_right contain the predefined and indexing values for each j; rol denotes left ; all additions and XORs are 2³².)

Known Weaknesses and Attacks

The original RIPEMD , proposed in 1992, was found to have significant weaknesses shortly after its publication. Hans Dobbertin demonstrated a on the reduced two-round version of its compression function, achieving collisions with a complexity of approximately 2182^{18} hash computations, which highlighted structural vulnerabilities in the and prompted the development of strengthened variants like RIPEMD-160. This attack exploited differential paths in the MD4-like structure, revealing that the parallel branch did not sufficiently mitigate propagation of differences, though it did not directly break the full three-round function in practical time. For RIPEMD-160, cryptanalytic efforts have focused on reduced-round variants, with no practical full collisions known as of 2025. In 2013, researchers presented a semi-free-start on 36 steps (out of 80) starting from the first step, with a practical of 2312^{31} compression function evaluations, using advanced differential path searches and message modification techniques tailored to the dual-branch architecture. This result demonstrated vulnerabilities in the early rounds but remained far from threatening the full function, as the complexity exceeds brute-force bounds only for the reduced version. Subsequent improvements in 2023 achieved a on 36 steps with 264.52^{64.5}, and a practical collision on 40 steps (found in 16 hours using 115 threads), using MILP to optimize differential characteristics and SAT/SMT solvers for message pair finding. In 2025, further advances presented semi-free-start collision attacks on up to 44 steps with complexity 276.92^{76.9}, including practical attacks on 41 steps (249.82^{49.8}) and 42 steps (253.92^{53.9}), employing enhanced automatic search models, differential clustering, and dedicated message modification techniques. These advances underscore ongoing concerns about the function's long-term security margin, though full collisions remain infeasible with current computational resources. Among other variants, RIPEMD-128 has been subjected to a pseudo-preimage attack on a 36-step reduced version with complexity 21232^{123}, and a with 2126.52^{126.5}, leveraging meet-in-the-middle techniques on the double-branch structure to find messages mapping to the same hash value more efficiently than generic bounds. In contrast, RIPEMD-256 and RIPEMD-320 have withstood significant and remain unbroken against practical collision or preimage attacks as of 2025, owing to their larger output sizes and enhanced round structures. Overall, while RIPEMD-160 resists practical full attacks, its age and the incremental progress in reduced-round cryptanalysis have led to recommendations against its use in new cryptographic systems, favoring modern alternatives with stronger proven security.

Comparison with Other Hash Functions

RIPEMD, developed as a European successor to the MD4 hash function, was designed to address vulnerabilities in the MD family, particularly MD5. While MD5, with its 128-bit output, succumbed to practical collision attacks with a complexity of approximately 2392^{39} operations as demonstrated by Wang et al. in 2004, RIPEMD-160 provides stronger resistance, maintaining its full 160-bit collision security at the birthday bound of 2802^{80} without known practical breaks. This makes RIPEMD-160 a more robust alternative for legacy systems requiring 160-bit hashes, though its design emphasizes parallel processing of two streams to enhance security margins over MD5's sequential approach. In comparison to the SHA family, RIPEMD-160 offers comparable output length to but superior practical security, as has been compromised with collisions achievable at 2632^{63} complexity via differential cryptanalysis by et al. in , leading to its . SHA-256, with a 256-bit output, achieves a higher of 21282^{128}, making it preferable for modern applications demanding long-term security. RIPEMD-160's 160-bit design thus provides 2802^{80} security, which is adequate for many uses but inferior to SHA-256 or SHA-512's 22562^{256} level against brute-force threats. Performance-wise, RIPEMD-160 is slower than on 32-bit systems, requiring about 1013 cycles per 512-bit block compared to 's 837 cycles on a processor, due to its dual-line computation. However, it outperforms on the same architecture, as 's 64-bit word operations incur overhead on 32-bit hardware, often doubling or tripling cycle counts relative to 32-bit-optimized hashes like RIPEMD-160. As of , RIPEMD-160 remains in legacy adoption, notably for address generation alongside , while faces full phase-out by 2030 per NIST guidelines, and / variants are recommended for new deployments.
Hash FunctionCollision ResistanceRelative Speed (32-bit Systems)Adoption Status (2025)
Broken (2392^{39})FastestDeprecated
RIPEMD-1602802^{80}Medium (1013 cycles/block)Legacy (e.g., )
Broken (2632^{63})Faster than RIPEMD-160 (837 cycles/block)Deprecated (phase-out by 2030)
SHA-25621282^{128}FastWidely used
SHA-51222562^{256}Slow (64-bit overhead)Widely used

Applications

Cryptographic Uses

RIPEMD-160 has been employed in schemes for , particularly within the OpenPGP protocol for creating and verifying signatures on electronic messages and files. Although newer implementations discourage its use for new signatures due to security considerations, it remains supported for compatibility in tools like GnuPG that handle legacy PGP keys. In certificate infrastructures, RIPEMD-160 has been utilized to hash certificate data before signing with algorithms such as RSA, appearing in some end-entity certificates for in public key infrastructures. A prominent application of RIPEMD-160 persists in technology, where it is integral to 's address generation process. To derive a address, the public key is first hashed with SHA-256, and the resulting 256-bit digest is then processed through RIPEMD-160 to produce a 160-bit hash, which is further encoded with versioning and checksums to form the final . This double-hashing approach enhances security by combining the strengths of both functions, and RIPEMD-160's role remains unchanged in 's protocol as of 2025, supporting the network's ongoing operations. In other protocols, RIPEMD-160 provides legacy support for cryptographic operations, such as in older SSL/TLS implementations where it could be selected as a for handshake integrity, though modern configurations favor SHA-based alternatives via providers like OpenSSL's legacy module. For file integrity verification, systems leverage RIPEMD-160 through command-line tools like OpenSSL's dgst -ripemd160 to compute checksums, ensuring data has not been altered during transfer or storage. However, its adoption has declined broadly following NIST recommendations to prioritize the and families for approved cryptographic s, citing their standardized security profiles over non-FIPS options like RIPEMD-160. RIPEMD-160 finds continued niche applications in resource-constrained environments, such as smart cards and embedded systems, where its 160-bit output provides adequate security for legacy-compatible while minimizing computational overhead compared to longer-hash alternatives. These deployments often pair it with hardware accelerators optimized for its parallel structure, suitable for scenarios like token verification or device signing where 160-bit suffices.

Software Implementations

RIPEMD-160 implementations are available in several prominent open-source cryptographic libraries, enabling integration into various software projects for legacy or specific use cases. The library provides support for RIPEMD-160 through its EVP_MD , though in version 3.0 and later, it is included in the legacy provider rather than the default one, requiring explicit loading for use. Bouncy Castle, a widely used library for and .NET environments, offers comprehensive RIPEMD-160 support via its provider classes, including digest computation and integration with JCA/JCE standards. Similarly, the Crypto++ C++ library includes a dedicated RIPEMD160 class for efficient message digest computation, supporting 160-bit output as part of its suite. Language-specific support for RIPEMD-160 is provided through standard or extended cryptographic APIs, often relying on underlying libraries like those mentioned above. In Python, the hashlib module allows creation of RIPEMD-160 hashes using hashlib.new('ripemd160'), though availability depends on the system's configuration, as newer versions (3.0+) may disable it by default. For example:

python

import hashlib data = b"Hello, RIPEMD-160!" h = hashlib.new('ripemd160') h.update(data) digest = h.hexdigest() print(digest) # Outputs the 40-character hex digest

import hashlib data = b"Hello, RIPEMD-160!" h = hashlib.new('ripemd160') h.update(data) digest = h.hexdigest() print(digest) # Outputs the 40-character hex digest

In , RIPEMD-160 can be accessed via java.security.MessageDigest.getInstance("RIPEMD160"), but this typically requires a third-party provider like Bouncy Castle, as it is not natively included in the JDK. A basic usage example with Bouncy Castle registered is:

java

import java.security.MessageDigest; import org.bouncycastle.jce.provider.BouncyCastleProvider; import java.security.Security; Security.addProvider(new BouncyCastleProvider()); MessageDigest md = MessageDigest.getInstance("RIPEMD160"); md.update("Hello, RIPEMD-160!".getBytes()); byte[] digest = md.digest(); System.out.println(bytesToHex(digest)); // Custom method to convert to hex

import java.security.MessageDigest; import org.bouncycastle.jce.provider.BouncyCastleProvider; import java.security.Security; Security.addProvider(new BouncyCastleProvider()); MessageDigest md = MessageDigest.getInstance("RIPEMD160"); md.update("Hello, RIPEMD-160!".getBytes()); byte[] digest = md.digest(); System.out.println(bytesToHex(digest)); // Custom method to convert to hex

Hardware support for RIPEMD remains limited and primarily software-based, with partial implementations in some smart card processors for legacy cryptographic operations, such as those based on ARM SecurCore architectures. Unlike SHA family hashes, RIPEMD-160 lacks dedicated hardware instructions in modern Intel or ARM CPUs, relying on general-purpose processing or FPGA-based accelerators for high-performance needs. Due to evolving standards, RIPEMD-160 is considered a legacy and has been deprecated in many modern cryptographic libraries and tools, though it persists for compatibility with systems like address generation.

References

  1. https://homes.esat.kuleuven.be/~bosselae/ripemd160.html
  2. https://www.sciencedirect.com/science/article/pii/S1110866512000357
  3. https://homes.esat.kuleuven.be/~bosselae/ripemd160/pdf/AB-9601/AB-9601.pdf
  4. https://eprint.iacr.org/2025/1531
  5. https://en.bitcoin.it/wiki/RIPEMD-160
  6. https://www.iso.org/standard/67116.html
  7. https://link.springer.com/chapter/10.1007/3-540-46416-6_52
  8. https://chaum.com/wp-content/uploads/2022/01/RaceIntegrityPrimitives.pdf
  9. https://link.springer.com/chapter/10.1007/3-540-60640-8_5
  10. https://link.springer.com/book/10.1007/3-540-60640-8
  11. https://eprint.iacr.org/2013/607.pdf
  12. https://www.researchgate.net/publication/2829058_RIPEMD-160_A_strengthened_version_of_RIPEMD
  13. https://www.iso.org/standard/39876.html
  14. https://tosc.iacr.org/index.php/ToSC/article/view/643/611
  15. https://link.springer.com/chapter/10.1007/3-540-60865-6_44
  16. https://homes.esat.kuleuven.be/~bosselae/ripemd/rmd160.txt
  17. A pseudo-preimage and second preimage attacks on the first 47 steps of RIPEMD (full version: 48 steps) are proposed with complexities of 2119 and 2124.5 ...
  18. https://link.springer.com/chapter/10.1007/978-3-642-42045-0_25
  19. https://eprint.iacr.org/2023/277
  20. https://eprint.iacr.org/2023/285
  21. https://link.springer.com/chapter/10.1007/978-3-642-19074-2_14
  22. https://eprint.iacr.org/2004/264.pdf
  23. https://eprint.iacr.org/2007/474
  24. https://www.nist.gov/news-events/news/2022/12/nist-retires-sha-1-cryptographic-algorithm
  25. https://datatracker.ietf.org/doc/html/rfc4880
  26. https://www.rfc-editor.org/rfc/rfc9580.html
  27. https://dicom.nema.org/medical/dicom/current/output/chtml/part15/chapter_c.html
  28. https://www.cs.auckland.ac.nz/~pgut001/pubs/x509guide.txt
  29. https://jtspratley.com/blog/creating-ripemd-160-checksums-in-linux
  30. https://csrc.nist.gov/projects/hash-functions/nist-policy-on-hash-functions
  31. https://www.researchgate.net/publication/222176557_ASIC-hardware-focused_comparison_for_hash_functions_MD5_RIPEMD-160_and_SHS
  32. https://docs.openssl.org/3.0/man7/EVP_MD-RIPEMD160/
  33. https://github.com/openssl/openssl/issues/17722
  34. https://downloads.bouncycastle.org/java/docs/bcprov-jdk15to18-javadoc/org/bouncycastle/jcajce/provider/digest/RIPEMD160.html
  35. https://www.bouncycastle.org/documentation/specification_interoperability/
  36. https://www.cryptopp.com/docs/ref/class_r_i_p_e_m_d160.html
  37. https://mojoauth.com/hashing/ripemd-160-in-java/
  38. https://developer.arm.com/documentation/PRD29-GENC-009492/latest/TrustZone-Hardware-Library/Processor-IP/SecurCore-smartcard-processors
  39. https://www.researchgate.net/publication/228703560_On_the_hardware_implementation_of_RIPEMD_processor_Networking_high_speed_hashing_up_to_2_Gbps
Add your contribution
Related Hubs
Contribute something
User Avatar
No comments yet.