Static single-assignment form

SSA was developed in the 1980s by several researchers at IBM. Kenneth Zadeck, a key member of the team, moved to Brown University as development continued.^[2][3] A 1986 paper introduced birthpoints, identity assignments, and variable renaming such that variables had a single static assignment.^[4] A subsequent 1987 paper by Jeanne Ferrante and Ronald Cytron^[5] proved that the renaming done in the previous paper removes all false dependencies for scalars.^[3] In 1988, Barry Rosen, Mark N. Wegman, and Kenneth Zadeck replaced the identity assignments with Φ-functions, introduced the name "static single-assignment form", and demonstrated a now-common SSA optimization.^[6] The name Φ-function was chosen by Rosen to be a more publishable version of "phony function".^[3] Alpern, Wegman, and Zadeck presented another optimization, but using the name "static single assignment".^[7] Finally, in 1989, Rosen, Wegman, Zadeck, Cytron, and Ferrante found an efficient means of converting programs to SSA form.^[8]

The primary usefulness of SSA comes from how it simultaneously simplifies and improves the results of a variety of compiler optimizations, by simplifying the properties of variables. For example, consider this piece of code:

y := 1
y := 2
x := y

Humans can see that the first assignment is not necessary, and that the value of y being used in the third line comes from the second assignment of y. A program would have to perform reaching definition analysis to determine this. But if the program is in SSA form, both of these are immediate:

y1 := 1
y2 := 2
x1 := y2

Compiler optimization algorithms that are either enabled or strongly enhanced by the use of SSA include:

• Constant folding – conversion of computations from runtime to compile time, e.g. treat the instruction a=3*4+5; as if it were a=17;
• Value range propagation^[9] – precompute the potential ranges a calculation could be, allowing for the creation of branch predictions in advance
• Sparse conditional constant propagation – range-check some values, allowing tests to predict the most likely branch
• Dead-code elimination – remove code that will have no effect on the results
• Global value numbering – replace duplicate calculations producing the same result
• Partial-redundancy elimination – removing duplicate calculations previously performed in some branches of the program
• Strength reduction – replacing expensive operations by less expensive but equivalent ones, e.g. replace integer multiply or divide by powers of 2 with the potentially less expensive shift left (for multiply) or shift right (for divide).
• Register allocation – optimize how the limited number of machine registers may be used for calculations

Converting ordinary code into SSA form is primarily a matter of replacing the target of each assignment with a new variable, and replacing each use of a variable with the "version" of the variable reaching that point. For example, consider the following control-flow graph:

Changing the name on the left hand side of "x ${\displaystyle \leftarrow }$ x - 3" and changing the following uses of x to that new name would leave the program unaltered. This can be exploited in SSA by creating two new variables: x₁ and x₂, each of which is assigned only once. Likewise, giving distinguishing subscripts to all the other variables yields:

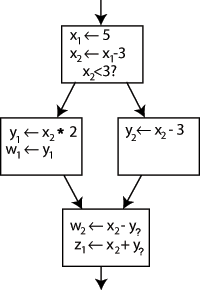
It is clear which definition each use is referring to, except for one case: both uses of y in the bottom block could be referring to either y₁ or y₂, depending on which path the control flow took.

To resolve this, a special statement is inserted in the last block, called a Φ (Phi) function. This statement will generate a new definition of y called y₃ by "choosing" either y₁ or y₂, depending on the control flow in the past.

Now, the last block can simply use y₃, and the correct value will be obtained either way. A Φ function for x is not needed: only one version of x, namely x₂ is reaching this place, so there is no problem (in other words, Φ(x₂,x₂)=x₂).

Given an arbitrary control-flow graph, it can be difficult to tell where to insert Φ functions, and for which variables. This general question has an efficient solution that can be computed using a concept called dominance frontiers (see below).

Φ functions are not implemented as machine operations on most machines. A compiler can implement a Φ function by inserting "move" operations at the end of every predecessor block. In the example above, the compiler might insert a move from y₁ to y₃ at the end of the middle-left block and a move from y₂ to y₃ at the end of the middle-right block. These move operations might not end up in the final code based on the compiler's register allocation procedure. However, this approach may not work when simultaneous operations are speculatively producing inputs to a Φ function, as can happen on wide-issue machines. Typically, a wide-issue machine has a selection instruction used in such situations by the compiler to implement the Φ function.

In a control-flow graph, a node A is said to strictly dominate a different node B if it is impossible to reach B without passing through A first. In other words, if node B is reached, then it can be assumed that A has run. A is said to dominate B (or B to be dominated by A) if either A strictly dominates B or A = B.

A node which transfers control to a node A is called an immediate predecessor of A.

The dominance frontier of node A is the set of nodes B where A does not strictly dominate B, but does dominate some immediate predecessor of B. These are the points at which multiple control paths merge back together into a single path.

For example, in the following code:

[1] x = random()
if x < 0.5
    [2] result = "heads"
else
    [3] result = "tails"
end
[4] print(result)

Node 1 strictly dominates 2, 3, and 4 and the immediate predecessors of node 4 are nodes 2 and 3.

Dominance frontiers define the points at which Φ functions are needed. In the above example, when control is passed to node 4, the definition of result used depends on whether control was passed from node 2 or 3. Φ functions are not needed for variables defined in a dominator, as there is only one possible definition that can apply.

There is an efficient algorithm for finding dominance frontiers of each node. This algorithm was originally described in "Efficiently Computing Static Single Assignment Form and the Control Graph" by Ron Cytron, Jeanne Ferrante, et al. in 1991.^[10]

Keith D. Cooper, Timothy J. Harvey, and Ken Kennedy of Rice University describe an algorithm in their paper titled A Simple, Fast Dominance Algorithm:^[11]

for each node b
    dominance_frontier(b) := {}
for each node b
    if the number of immediate predecessors of b ≥ 2
        for each p in immediate predecessors of b
            runner := p
            while runner ≠ idom(b)
                dominance_frontier(runner) := dominance_frontier(runner) ∪ { b }
                runner := idom(runner)

In the code above, idom(b) is the immediate dominator of b, the unique node that strictly dominates b but does not strictly dominate any other node that strictly dominates b.

"Minimal" SSA inserts the minimal number of Φ functions required to ensure that each name is assigned a value exactly once and that each reference (use) of a name in the original program can still refer to a unique name. (The latter requirement is needed to ensure that the compiler can write down a name for each operand in each operation.)

However, some of these Φ functions could be dead. For this reason, minimal SSA does not necessarily produce the fewest Φ functions that are needed by a specific procedure. For some types of analysis, these Φ functions are superfluous and can cause the analysis to run less efficiently.

Pruned SSA form is based on a simple observation: Φ functions are only needed for variables that are "live" after the Φ function. (Here, "live" means that the value is used along some path that begins at the Φ function in question.) If a variable is not live, the result of the Φ function cannot be used and the assignment by the Φ function is dead.

Construction of pruned SSA form uses live-variable information in the Φ function insertion phase to decide whether a given Φ function is needed. If the original variable name isn't live at the Φ function insertion point, the Φ function isn't inserted.

Another possibility is to treat pruning as a dead-code elimination problem. Then, a Φ function is live only if any use in the input program will be rewritten to it, or if it will be used as an argument in another Φ function. When entering SSA form, each use is rewritten to the nearest definition that dominates it. A Φ function will then be considered live as long as it is the nearest definition that dominates at least one use, or at least one argument of a live Φ.

Semi-pruned SSA form^[12] is an attempt to reduce the number of Φ functions without incurring the relatively high cost of computing live-variable information. It is based on the following observation: if a variable is never live upon entry into a basic block, it never needs a Φ function. During SSA construction, Φ functions for any "block-local" variables are omitted.

Computing the set of block-local variables is a simpler and faster procedure than full live-variable analysis, making semi-pruned SSA form more efficient to compute than pruned SSA form. On the other hand, semi-pruned SSA form will contain more Φ functions.

Block arguments are an alternative to Φ functions that is representationally identical but in practice can be more convenient during optimization. Blocks are named and take a list of block arguments, notated as function parameters. When calling a block the block arguments are bound to specified values. MLton, Swift SIL, and LLVM MLIR use block arguments.^[13]

SSA form is not normally used for direct execution (although it is possible to interpret SSA^[14]), and it is frequently used "on top of" another IR with which it remains in direct correspondence. This can be accomplished by "constructing" SSA as a set of functions that map between parts of the existing IR (basic blocks, instructions, operands, etc.) and its SSA counterpart. When the SSA form is no longer needed, these mapping functions may be discarded, leaving only the now-optimized IR.

Performing optimizations on SSA form usually leads to entangled SSA-Webs, meaning there are Φ instructions whose operands do not all have the same root operand. In such cases color-out algorithms are used to come out of SSA. Naive algorithms introduce a copy along each predecessor path that caused a source of different root symbol to be put in Φ than the destination of Φ. There are multiple algorithms for coming out of SSA with fewer copies, most use interference graphs or some approximation of it to do copy coalescing.^[15]

Extensions to SSA form can be divided into two categories.

Renaming scheme extensions alter the renaming criterion. Recall that SSA form renames each variable when it is assigned a value. Alternative schemes include static single use form (which renames each variable at each statement when it is used) and static single information form (which renames each variable when it is assigned a value, and at the post-dominance frontier).

Feature-specific extensions retain the single assignment property for variables, but incorporate new semantics to model additional features. Some feature-specific extensions model high-level programming language features like arrays, objects and aliased pointers. Other feature-specific extensions model low-level architectural features like speculation and predication.

This section may contain excessive or irrelevant examples. Please help improve it by removing less pertinent examples and elaborating on existing ones. (August 2018) (Learn how and when to remove this message)

• Mono uses SSA in its JIT compiler called Mini
• WebKit uses SSA in its JIT compilers.^[16][17]
• Swift defines its own SSA form above LLVM IR, called SIL (Swift Intermediate Language).^[18][19]
• The Erlang compiler was rewritten in OTP 22.0 to "internally use an intermediate representation based on Static Single Assignment (SSA)", with plans for further optimizations built on top of SSA in future releases.^[20]
• The LLVM Compiler Infrastructure uses SSA form for all scalar register values (everything except memory) in its primary code representation. SSA form is only eliminated once register allocation occurs, late in the compile process (often at link time).
• The GNU Compiler Collection (GCC) makes extensive use of SSA since version 4 (released in April 2005). The frontends generate "GENERIC" code that is then converted into "GIMPLE" code by the "gimplifier". High-level optimizations are then applied on the SSA form of "GIMPLE". The resulting optimized intermediate code is then translated into RTL, on which low-level optimizations are applied. The architecture-specific backends finally turn RTL into assembly language.
• Go (1.7: for x86-64 architecture only; 1.8: for all supported architectures).^[21][22]
• IBM's open source adaptive Java virtual machine, Jikes RVM, uses extended Array SSA, an extension of SSA that allows analysis of scalars, arrays, and object fields in a unified framework. Extended Array SSA analysis is only enabled at the maximum optimization level, which is applied to the most frequently executed portions of code.
• The Mozilla Firefox SpiderMonkey JavaScript engine uses SSA-based IR.^[23]
• The Chromium V8 JavaScript engine implements SSA in its Crankshaft compiler infrastructure as announced in December 2010
• PyPy uses a linear SSA representation for traces in its JIT compiler.
• The Android Runtime^[24] and the Dalvik Virtual Machine use SSA.^[25]
• The Standard ML compiler MLton uses SSA in one of its intermediate languages.
• LuaJIT makes heavy use of SSA-based optimizations.^[26]
• The PHP and Hack compiler HHVM uses SSA in its IR.^[27]
• The OCaml compiler uses SSA in its CMM IR (which stands for C--).^[28]
• libFirm, a library for use as the middle and back ends of a compiler, uses SSA form for all scalar register values until code generation by use of an SSA-aware register allocator.^[29]
• Various Mesa drivers via NIR, an SSA representation for shading languages.^[30]

• Oracle's HotSpot Java Virtual Machine uses an SSA-based intermediate language in its JIT compiler.^[31]
• Microsoft Visual C++ compiler backend available in Microsoft Visual Studio 2015 Update 3 uses SSA^[32]
• SPIR-V, the shading language standard for the Vulkan graphics API and kernel language for OpenCL compute API, is an SSA representation.^[33]
• The IBM family of XL compilers, which include C, C++ and Fortran.^[34]
• NVIDIA CUDA^[35]

• The ETH Oberon-2 compiler was one of the first public projects to incorporate "GSA", a variant of SSA.
• The Open64 compiler used SSA form in its global scalar optimizer, though the code is brought into SSA form before and taken out of SSA form afterwards. Open64 uses extensions to SSA form to represent memory in SSA form as well as scalar values.
• In 2002, researchers modified IBM's JikesRVM (named Jalapeño at the time) to run both standard Java bytecode and a typesafe SSA (SafeTSA) bytecode class files, and demonstrated significant performance benefits to using the SSA bytecode.
• jackcc is an open-source compiler for the academic instruction set Jackal 3.0. It uses a simple 3-operand code with SSA for its intermediate representation. As an interesting variant, it replaces Φ functions with a so-called SAME instruction, which instructs the register allocator to place the two live ranges into the same physical register.
• The Illinois Concert Compiler circa 1994^[36] used a variant of SSA called SSU (Static Single Use) which renames each variable when it is assigned a value, and in each conditional context in which that variable is used; essentially the static single information form mentioned above. The SSU form is documented in John Plevyak's Ph.D Thesis.
• The COINS compiler uses SSA form optimizations as explained here.
• Reservoir Labs' R-Stream compiler supports non-SSA (quad list), SSA and SSI (Static Single Information^[37]) forms.^[38]
• Although not a compiler, the Boomerang decompiler uses SSA form in its internal representation. SSA is used to simplify expression propagation, identifying parameters and returns, preservation analysis, and more.
• DotGNU Portable.NET used SSA in its JIT compiler.