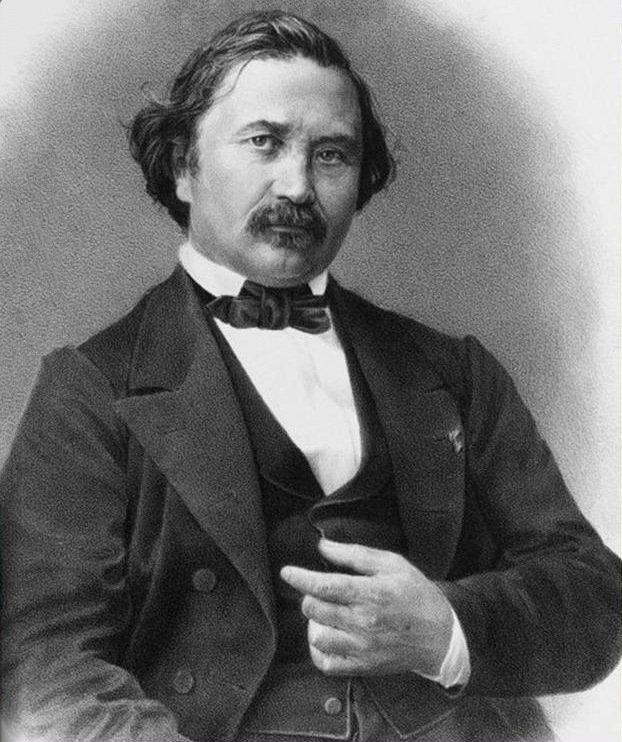Hubbry Logo
Joseph BertrandJoseph BertrandMain
Open search
Joseph Bertrand
Community hub
Joseph Bertrand
logo
8 pages, 0 posts
0 subscribers
Be the first to start a discussion here.
Be the first to start a discussion here.
Joseph Bertrand
Joseph Bertrand
Joseph Bertrand
View on Wikipedia
from Wikipedia

Joseph Louis François Bertrand (French pronunciation: [ʒozɛf lwi fʁɑ̃swa bɛʁtʁɑ̃]; 11 March 1822 – 5 April 1900) was a French mathematician and historian of science whose work emphasized number theory, differential geometry, probability theory, economics and thermodynamics.[1]

Key Information

Biography

[edit]

Joseph Bertrand was the son of physician Alexandre Jacques François Bertrand and the brother of archaeologist Alexandre Bertrand. His father died when Joseph was only nine years old; by that time he had learned a substantial amount of mathematics and could speak Latin fluently. At eleven years old he attended the course of the École Polytechnique as an auditor. From age eleven to seventeen, he obtained two bachelor's degrees, a license and a PhD with a thesis concerning the mathematical theory of electricity, and was admitted to the 1839 entrance examination of the École Polytechnique. Bertrand was a professor at the École Polytechnique and Collège de France, and was a member of the Paris Academy of Sciences of which he was the permanent secretary for twenty-six years.

He conjectured, in 1845, that there is at least one prime number between n and 2n − 2 for every n > 3. Chebyshev proved this conjecture, now termed Bertrand's postulate, in 1850. He was also famous for two paradoxes of probability, known now as Bertrand's Paradox and the Paradox of Bertrand's box. There is another paradox concerning game theory that is named for him, known as the Bertrand Paradox. In 1849, he was the first to define real numbers using what is now termed a Dedekind cut.[2][3]

Bertrand translated into French Carl Friedrich Gauss's work concerning the theory of errors and the method of least squares.

Concerning economics, he reviewed the work on oligopoly theory, specifically the Cournot Competition Model (1838) of French mathematician Antoine Augustin Cournot. His Bertrand Competition Model (1883) argued that Cournot had reached a very misleading conclusion, and he reworked it using prices rather than quantities as the strategic variables, thus showing that the equilibrium price was simply the competitive price.

His book Thermodynamique states in Chapter XII, that thermodynamic entropy and temperature are only defined for reversible processes. He was one of the first people to state this publicly.

In 1858 he was elected a foreign member of the Royal Swedish Academy of Sciences.

Works by Bertrand

[edit]

See also

[edit]

Further reading

[edit]

References

[edit]
[edit]
Revisions and contributorsEdit on WikipediaRead on Wikipedia

Joseph Bertrand

View on Grokipedia
from Grokipedia
Joseph Louis François Bertrand (11 March 1822 – 3 April 1900) was a French mathematician and educator whose prolific work spanned , probability, , , and . A who earned a doctorate at age 17, Bertrand made foundational contributions including the conjecture now known as Bertrand's postulate—stating that for every integer n > 1, there exists at least one prime p such that n < p ≤ 2n—and the introduction of Bertrand's paradox, which highlights ambiguities in defining uniform probability distributions on continuous spaces. His rigorous applications of differential equations to mechanics and heat theory also influenced 19th-century physics, while his critique of economic models led to the development of the Bertrand duopoly model, emphasizing price competition in oligopolies. Born in Paris to a family of intellectuals—his father Alexandre was a science writer and his sister Louise married mathematician Charles Hermite—Bertrand displayed exceptional talent early, completing a bachelor's degree at 16 and defending a thesis on thermomechanics in 1839. He studied at the École Polytechnique (1839–1841) and École des Mines (1841–1844), then began a distinguished academic career teaching at the Lycée Saint-Louis (1841–1848), Lycée Henry IV (from 1852), École Polytechnique (as professor from 1856), École Normale Supérieure, and Collège de France (analysis chair from 1862). Elected to the Paris Academy of Sciences in 1856, and to the Académie française in 1884, he served as its permanent secretary from 1874 until his death, was made a Grand Officer of the Légion d'Honneur, and received a gold medal in 1895 for 50 years of teaching service. Despite personal setbacks, including injuries from a 1842 train accident and the loss of manuscripts in the 1871 Paris Commune fire, Bertrand mentored figures like Henri Poincaré and authored influential textbooks that shaped mathematical education. Bertrand's mathematical legacy includes early work on group theory, such as studies of subgroups in symmetric groups (1845), and differential geometry, notably memoirs on isothermal surfaces (1843). In probability, his 1888 treatise Calcul des probabilités formalized concepts like the ballot theorem and critiqued intuitive probability measures, inspiring later developments in stochastic processes. Economically, in an 1883 review of Léon Walras's work, he reformulated Antoine-Augustin Cournot's duopoly model by assuming firms compete on price rather than quantity, yielding marginal-cost pricing outcomes that prefigured modern game theory. His thermodynamics research, including Théorie des problèmes thermomécaniques (1839), applied calculus to heat and elasticity, bridging mathematics and physical sciences. Bertrand's clear, pedagogical style in works like Traité de calcul différentiel et de calcul intégral (1864–1870) ensured lasting impact on analysis and algebra education.

Early Life and Education

Family Background and Childhood

Joseph Louis François Bertrand was born on 11 March 1822 in Paris, France, to Alexandre Jacques François Bertrand, a physician and author of popular science works who had studied at the École Polytechnique, and Marie Caroline Belin. His family environment fostered an early interest in intellectual pursuits, with his father's background in medicine and science providing a stimulating backdrop during his formative years. Bertrand's childhood was marked by tragedy when his father died in 1831, at which point he was nine years old, prompting him to live with the family of mathematician Jean-Marie Constant Duhamel, a close friend of his father and professor at the École Polytechnique. Duhamel, who had married Bertrand's aunt (his father's sister), offered a supportive home that further nurtured his emerging talents. Bertrand had a brother, Alexandre Bertrand, who later became a noted archaeologist, and a sister, Louise, who married mathematician in 1848. By age nine, Bertrand had already demonstrated prodigious ability, mastering algebra, elementary geometry, and fluent Latin, skills that highlighted his exceptional aptitude for mathematics and languages. At eleven, he began attending lectures at the École Polytechnique unofficially, gaining early exposure to advanced topics under Duhamel's influence.

Academic Training

Joseph Louis François Bertrand demonstrated exceptional precocity in his academic pursuits, earning his first degree from the University of Paris at the age of 16 in 1838. The following year, at age 17, he received his doctorate from the École Polytechnique with a dissertation titled Sur la théorie des phénomènes thermo-mécaniques, which explored the mathematical foundations of thermodynamics and related mechanical phenomena. This achievement came shortly after his father's death in 1831, when family support and the guardianship of mathematician Jean-Marie Duhamel enabled Bertrand to continue his studies without interruption. Bertrand's formal entry into the École Polytechnique occurred in 1839, though he had informally attended lectures there since the age of 11 in 1833, immersing himself in the institution's rigorous curriculum emphasizing mathematical analysis and geometry. Under the influence of figures like Duhamel, who provided personal mentorship from 1831 onward, Bertrand developed a strong foundation in pure and applied mathematics during these years. His early exposure to advanced topics fostered an intellectual environment that highlighted analytical rigor and geometric intuition, shaping his lifelong approach to mathematical problems. During his student years, Bertrand produced his initial scholarly work, including his first publication in 1839—a paper titled Note sur quelques points de la théorie de l'électricité, addressing key aspects of the mathematical theory of electricity. This was followed by presentations of memoirs to the Académie des Sciences in 1843 on isothermal orthogonal surfaces, demonstrating his emerging expertise in differential geometry while still enrolled as a student. From 1841 to 1844, Bertrand pursued studies at the École des Mines, where the program focused on applied mathematics and engineering principles, complementing his theoretical training at the École Polytechnique. This period solidified his ability to bridge abstract mathematics with practical applications, particularly in areas like thermodynamics and electricity that had featured in his doctoral work.

Professional Career

Initial Appointments

In 1841, shortly after entering the École des Mines to pursue engineering studies, Joseph Bertrand was appointed professor of elementary mathematics at the Lycée Saint-Louis in Paris, a role he maintained until 1848 while balancing his academic training. This early teaching position allowed him to support himself and gain practical experience in instruction, focusing on foundational mathematical concepts for secondary students. By 1844, Bertrand had advanced within the prestigious École Polytechnique, where his doctoral thesis from 1839 on the mathematical theory of electricity provided a strong basis for his appointment as répétiteur d'analyse. In this capacity, he assisted in delivering advanced analysis courses to elite engineering cadets, honing his expertise in calculus and related fields that would define his later career. The political upheavals of 1848 interrupted his routine when Bertrand briefly served as a captain in the National Guard during the February Revolution, which overthrew the July Monarchy and established the Second Republic. This short military engagement underscored the era's instability but did not derail his academic progress. Amid these early roles, Bertrand made a notable scholarly contribution in 1845 with his memoir "Mémoire sur le nombre de valeurs que peut prendre une fonction quand on y permute les lettres qu'elle renferme," submitted to the Paris Academy of Sciences. The work examined subgroups of low index in the symmetric group through permutation analysis, earning a positive review from Augustin-Louis Cauchy, who praised its originality and depth. This publication marked Bertrand's initial foray into group-theoretic ideas, though formal recognition from academies came later in his career.

Major Professorships and Roles

In 1852, Joseph Bertrand was appointed professor of special mathematics at the Lycée Henry IV, where he also began teaching at the École Normale Supérieure, roles that allowed him to shape the training of future French mathematicians during a period of institutional reform in higher education. These positions built on his earlier experience as a répétiteur in analysis at the École Polytechnique starting in 1844, serving as a foundational step toward more prominent academic responsibilities. Bertrand's career advanced significantly in 1856 when he succeeded Charles-François Sturm as full professor of analysis at the École Polytechnique, a post he held until 1895, during which he lectured on advanced topics for over four decades and influenced generations of engineers and scholars. Concurrently, in 1853, he undertook a key scholarly role by editing and annotating the third edition of Joseph-Louis Lagrange's Mécanique analytique, a two-volume work published by Mallet-Bachelier that preserved and clarified foundational texts in analytical mechanics for contemporary students. In 1862, Bertrand was appointed to the chair of analysis at the Collège de France, succeeding , where he delivered lectures on mathematical analysis and probability that emphasized rigorous foundations and practical applications, contributing to the institution's reputation as a hub for advanced theoretical instruction. He ceased teaching there in 1878 but resumed the role in 1886, extending his tenure until his death and reinforcing the chair's focus on probabilistic methods amid evolving scientific demands. Through these professorships, Bertrand exerted a profound influence on French mathematical education, notably mentoring Henri Poincaré, whose 1896 Calcul des probabilités drew heavily from Bertrand's lectures on analysis and probability, establishing a direct lineage in the development of modern French approaches to these fields.

Administrative Positions and Honors

Bertrand was elected to membership in the Paris Academy of Sciences in 1856, following the death of Charles-François Sturm, a position that recognized his early contributions to mathematics. He later served as the Academy's permanent secretary for the mathematical section from 1874 until his death in 1900, a role spanning 26 years during which he exerted significant influence over French scientific discourse. In this capacity, Bertrand played a key part in academy politics, reviewing and promoting important works, including his 1855 French translation of 's writings on the theory of errors and the method of least squares, which helped disseminate these foundational statistical concepts to a broader audience. Beyond France, Bertrand was elected a foreign member of the in 1858, affirming his international reputation in pure mathematics. His administrative leadership extended to publicizing mathematical advancements in the late 19th century, as he leveraged his secretary position to highlight seminal developments and foster institutional support for the discipline. Bertrand received numerous honors for his career, including promotion to grand-officier in the Légion d'Honneur, one of France's highest distinctions. In 1895, marking 50 years of teaching at the École Polytechnique—where he had begun as a répétiteur in 1844—his former students presented him with a commemorative medal, underscoring his enduring impact as an educator and institution builder.

Mathematical Contributions

Number Theory

Joseph Bertrand's most renowned contribution to number theory is his 1845 conjecture, now known as Bertrand's Postulate, which asserts that for every integer n>1n > 1, there exists at least one pp such that n<p≤2nn < p \leq 2n. Originally stated for n>3n > 3 in a presented to the Paris Academy of Sciences, the result provides a guarantee on the existence of primes in short intervals and reflects the era's growing interest in prime distribution following earlier estimates by and . Bertrand verified the conjecture computationally for small values up to n<3,000,000n < 3,000,000, building on tables of primes compiled by earlier mathematicians. The conjecture remained unproved until Pafnuty Chebyshev established it in 1852 as part of his broader analysis of the prime-counting function π(x)\pi(x), demonstrating bounds that imply the postulate. Chebyshev's proof utilized properties of the binomial coefficients and Stirling's approximation to control the growth of π(x)\pi(x). In 1920, Srinivasa Ramanujan provided a shorter advanced proof; in 1932, Paul Erdős provided the first elementary proof, avoiding advanced analytic tools and making the result more accessible—this work marked Erdős's debut publication. Subsequent simplifications further refined the elementary argument. Bertrand's Postulate has implications for the prime number theorem, offering an explicit lower bound on prime density that aligns with the theorem's asymptotic π(x)∼x/ln⁡x\pi(x) \sim x / \ln x; it ensures that prime gaps are at most on the order of the numbers themselves, aiding approximations in analytic number theory. In his 1849 textbook Traité d'Arithmétique, Bertrand advanced the foundations of arithmetic by addressing irrational numbers, defining them through partitions of the rational numbers into sets of those less than and greater than the irrational, an approach akin to later developments in real number construction. This treatment complemented his early investigations into arithmetic progressions and prime gaps, inspired by Legendre's conjectures on π(x)\pi(x) and Gauss's logarithmic estimates, which highlighted patterns in prime occurrences and influenced Bertrand's focus on interval-based prime existence.

Probability and Statistics

Joseph Bertrand made significant contributions to probability theory through his comprehensive treatise Calcul des probabilités, published in 1888, which synthesized forty years of his lectures at the École Polytechnique and the Collège de France. This work emphasized the classical interpretation of probability, where outcomes are deemed equally likely, while acknowledging a subjective dimension by describing probability as "a measure of our ignorance" in assessing uncertain events. Bertrand applied these principles extensively to games of chance, such as lotteries and card games, demonstrating how probabilistic reasoning could resolve apparent uncertainties in practical scenarios like gambling strategies and insurance calculations. His innovations in probability calculus highlighted the need for precise definitions in continuous spaces, influencing later developments in measure-theoretic probability. One of Bertrand's most enduring contributions is the paradox he posed in Calcul des probabilités, known as Bertrand's paradox, which illustrates ambiguities in defining uniform probability distributions over continuous geometric objects. The problem considers an equilateral triangle inscribed in a circle of radius rr, with side length s=r3s = r\sqrt{3}
Add your contribution
Related Hubs
User Avatar
No comments yet.