Multiple edges

Multiple edgesMain

Community hub

Multiple edges

8 pages, 0 posts

0 subscribers

Recent from talks

Be the first to start a discussion here.

Recent from talks

Be the first to start a discussion here.

Contribute something

About hubMembersContent overviewUpdatesRules

Main reference articles

Multiple edges

View on Wikipedia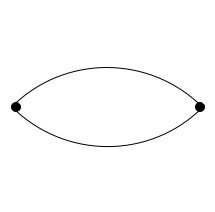

from Wikipedia

In graph theory, multiple edges (also called parallel edges or a multi-edge), are, in an undirected graph, two or more edges that are incident to the same two vertices, or in a directed graph, two or more edges with both the same tail vertex and the same head vertex. A simple graph has no multiple edges and no loops.

Depending on the context, a graph may be defined so as to either allow or disallow the presence of multiple edges (often in concert with allowing or disallowing loops):

Where graphs are defined so as to allow multiple edges and loops, a graph without loops or multiple edges is often distinguished from other graphs by calling it a simple graph.^[1]
Where graphs are defined so as to disallow multiple edges and loops, a multigraph or a pseudograph is often defined to mean a "graph" which can have multiple edges.^[2]

Multiple edges are, for example, useful in the consideration of electrical networks, from a graph theoretical point of view.^[3] Additionally, they constitute the core differentiating feature of multidimensional networks.

A planar graph remains planar if an edge is added between two vertices already joined by an edge; thus, adding multiple edges preserves planarity.^[4]

A dipole graph is a graph with two vertices, in which all edges are parallel to each other.

Notes

[edit]

^ For example, see Balakrishnan, p. 1, and Gross (2003), p. 4, Zwillinger, p. 220.
^ For example, see Bollobás, p. 7; Diestel, p. 28; Harary, p. 10.
^ Bollobás, pp. 39–40.
^ Gross (1998), p. 308.

References

[edit]

Balakrishnan, V. K.; Graph Theory, McGraw-Hill; 1 edition (February 1, 1997). ISBN 0-07-005489-4.
Bollobás, Béla; Modern Graph Theory, Springer; 1st edition (August 12, 2002). ISBN 0-387-98488-7.
Diestel, Reinhard; Graph Theory, Springer; 2nd edition (February 18, 2000). ISBN 0-387-98976-5.
Gross, Jonathon L, and Yellen, Jay; Graph Theory and Its Applications, CRC Press (December 30, 1998). ISBN 0-8493-3982-0.
Gross, Jonathon L, and Yellen, Jay; (eds); Handbook of Graph Theory. CRC (December 29, 2003). ISBN 1-58488-090-2.
Zwillinger, Daniel; CRC Standard Mathematical Tables and Formulae, Chapman & Hall/CRC; 31st edition (November 27, 2002). ISBN 1-58488-291-3.

Revisions and contributors Edit on Wikipedia Read on Wikipedia

View on Grokipedia

from Grokipedia

In graph theory, multiple edges, also known as parallel edges, refer to two or more edges that connect the same pair of vertices in a graph, distinguishing multigraphs from simple graphs that permit at most one undirected edge between any two distinct vertices.^[1]^[2] This structure allows for the representation of repeated or weighted connections without relying on edge labels or weights alone.^[1] Multiple edges can exist in both undirected and directed graphs, where in the directed case, they represent multiple arcs from one vertex to another.^[1]^[2] Multigraphs incorporating multiple edges are essential for modeling real-world scenarios involving multiplicity, such as multiple transportation routes between cities or multiple types of interactions in social networks.^[3]^[4] In incidence matrices, the multiplicity

d_{ij}

between vertices

i

and

j

is recorded as an integer greater than 1, influencing properties like vertex degrees, which sum all incident edges including multiples.^[1]^[5] Loops, which are edges from a vertex to itself, are sometimes treated separately but can also exhibit multiplicity in pseudographs, a subtype of multigraphs.^[1]^[2] The study of multiple edges impacts graph algorithms and theorems, such as edge coloring, where the chromatic index may equal the maximum degree or maximum multiplicity plus the maximum degree in certain cases, with applications in scheduling and resource allocation.^[6]^[1] Condensation techniques simplify multigraphs by reducing multiple edges to single edges, aiding analysis while preserving connectivity.^[7] Overall, multiple edges extend the expressive power of graphs beyond simple structures, enabling more accurate representations in fields like computer science, operations research, and network analysis.^[4]^[3]

Definitions and Basic Concepts

Undirected multiple edges

In undirected graphs, multiple edges, also known as parallel edges, consist of two or more edges that connect the same unordered pair of vertices without any specified direction.^[1]^[8] This configuration distinguishes them from simple graphs, where at most one edge is allowed between any two vertices.^[9] Such edges are fundamental in modeling real-world systems where repeated connections between entities are meaningful, such as multiple pathways in a transportation network or redundant links in communication systems. For example, consider an undirected graph with vertices labeled A and B connected by three distinct edges; this setup can represent three parallel bus routes between two cities, highlighting capacity or backup options in the network.^[10]^[11] In graphical depictions, multiple edges between a pair of vertices are typically illustrated as several distinct lines or curved arcs linking the two points, often positioned parallel to one another and occasionally labeled (e.g., with numbers or identifiers) to differentiate them visually.^[12] This representation aids in distinguishing the multiplicity while maintaining clarity in the diagram, assuming familiarity with basic undirected graphs comprising vertices and single edges.^[13]

Directed multiple edges

In graph theory, directed multiple edges, also known as multiple arcs, refer to the presence of two or more directed edges sharing the same ordered pair of vertices, from an initial vertex

u

to a terminal vertex

v

.^[12] This structure extends the concept of multigraphs to directed graphs, where arcs explicitly encode orientation.^[14] Unlike their undirected counterparts, which treat edges as symmetric and non-oriented, directed multiple arcs distinguish between directions, permitting multiples solely from

u

v

, or bidirectionally if arcs exist in both orientations between the pair.^[14] Formally, a directed multigraph allowing multiple arcs is defined as an ordered pair

(V, E)

consisting of a vertex set

V

and an edge set

E

, together with an incidence function

f: E \to V \times V

that maps each arc to an ordered pair

(u, v)

; arcs

e_1

and

e_2

are multiple if

f(e_1) = f(e_2) = (u, v)

.^[12] The multiplicity of such an arc pair is simply the number of distinct edges mapped to that ordered pair.^[12] A representative application appears in flow networks, where multiple arcs from a source vertex

S

to a sink vertex

T

model parallel transportation paths, each with its own capacity constraint to represent distinct routes or resources.^[15] For instance, in a capacitated network, two arcs from

S

T

might carry capacities of 5 and 3 units, respectively, allowing the total flow to aggregate up to 8 units along that direct connection while respecting individual limits.^[15] This setup is crucial for optimizing resource allocation in transportation or communication systems.^[15]

Multigraphs and Graph Types

Definition of multigraphs

In graph theory, a multigraph is formally defined as an ordered triple

G = (V(G), E(G), \psi_G)

, where

V(G)

is a nonempty finite set of vertices,

E(G)

is a finite set of edges disjoint from

V(G)

, and

\psi_G: E(G) \to \binom{V(G)}{2} \cup \{ \{v\} \mid v \in V(G) \}

is an incidence function that maps each edge to an unordered pair of vertices (possibly the same vertex, allowing loops) or a single vertex for loops.^[16] This structure permits multiple edges, known as parallel edges, between the same pair of vertices, distinguishing it from simpler graph forms.^[16] Variants of multigraphs include simple multigraphs, which prohibit loops but allow multiple edges between distinct vertices, and pseudographs, which extend this by explicitly permitting both multiple edges and loops.^[16] Multigraphs can also be undirected, using unordered pairs for edge endpoints, or directed (digraphs or multidigraphs), where the incidence function maps edges to ordered pairs

(u, v)

with

u, v \in V(G)

, allowing multiple directed edges from one vertex to another.^[16] Multigraphs generalize simple graphs by relaxing the restriction of at most one edge between any pair of vertices, enabling more flexible modeling of relationships in combinatorial structures.^[8]

Distinction from simple graphs

A simple graph is defined as an undirected graph with no loops and at most one edge connecting any pair of distinct vertices.^[17]^[18] This structure assumes unique connections between vertices, prohibiting both self-loops and parallel edges.^[12] The primary distinction lies in the allowance of multiple edges: simple graphs strictly forbid them, along with loops, to maintain a sparse and unique adjacency model, whereas multigraphs explicitly permit multiple edges between the same pair of vertices (and often loops) to capture repeated or parallel relationships.^[18]^[19] This flexibility in multigraphs addresses limitations in simple graphs, where modeling scenarios with redundancy—such as multiple pathways in transportation networks or duplicate links in communication systems—requires either artificial weights or approximations that obscure distinct interactions.^[20]^[17] Simple graphs excel in theoretical analyses focused on connectivity and basic structural properties, as their constraints simplify proofs and computations without loss of essential uniqueness.^[17] However, they fall short in applications demanding explicit representation of multiplicity, like parallel capacities in flow networks or redundant edges in reliability models, where multigraphs offer a more precise and direct encoding.^[20] To bridge this gap, multigraphs can be converted to simple graphs conceptually by techniques such as removing loops and retaining a single representative edge per pair, or through edge contraction to consolidate parallels into weighted or merged structures, though such transformations may alter original multiplicities and require careful interpretation.^[17] Labeling parallel edges with identifiers provides another approach to embed multiplicity within a simple graph framework for algorithmic compatibility.^[21]

Properties and Measures

Edge multiplicity

In graph theory, the multiplicity of an edge, denoted

m(u,v)

, is defined as the number of edges connecting two distinct vertices

u

and

v

in an undirected multigraph, or the number of directed arcs from

u

v

in a directed multigraph.^[22] This measure quantifies the extent to which multiple edges exist between a specific pair of vertices, distinguishing multigraphs from simple graphs where multiplicity is at most 1.^[23] The total number of edges

|E|

in an undirected multigraph is given by the formula

|E| = \sum_{\{u,v\} \subseteq V, \, u \neq v} m(u,v) + \sum_{u \in V} m(u,u),

where the first sum is over all unordered pairs of distinct vertices and the second accounts for loops if permitted, with each loop at vertex

u

contributing to

m(u,u)

.^[22] In a directed multigraph, the total number of arcs is instead

|E| = \sum_{(u,v) \in V \times V} m(u,v),

summing over all ordered pairs, including possible loops where

u = v

.^[23] These formulas encapsulate how multiplicity aggregates to the overall edge count in multigraphs, where multiplicity exceeds 1 for pairs with parallel connections.^[24] For example, if

m(u,v) = 0

, no edge exists between

u

and

v

, indicating an absent connection; whereas

m(u,v) > 1

signifies the presence of multiple parallel edges, such as two or more arcs from

u

v

in a directed case.^[22] A special case arises with loops, where the multiplicity

m(u,u)

represents the number of self-connecting edges at vertex

u

, allowed in some multigraph definitions to model reflexive relations.^[25]

Degree in the presence of multiple edges

In multigraphs, the degree of a vertex accounts for the presence of multiple edges and loops by summing the incidences with multiplicity. For an undirected multigraph without loops, the degree of a vertex

v

, denoted

\deg(v)

, is given by

\deg(v) = \sum_{u \in V, u \neq v} m(v,u)

, where

m(v,u)

is the multiplicity of edges between

v

and

u

, and

V

is the vertex set.^[22] When loops are permitted, each loop at

v

contributes 2 to

\deg(v)

, reflecting its two endpoints at the same vertex, so the full degree is

\deg(v) = \sum_{u \in V, u \neq v} m(v,u) + 2 \cdot l(v)

, where

l(v)

is the number of loops at

v

.^[22] For example, consider an undirected multigraph where vertex

v

has two edges connecting it to another vertex

u

(so

m(v,u) = 2

) and one loop at

v

(so

l(v) = 1

). The degree is then

\deg(v) = 2 + 2 \cdot 1 = 4

.^[22] In directed multigraphs, degrees are separated into in-degree and out-degree to reflect edge directions. The out-degree of

v

\deg^+(v) = \sum_{u \in V} m^+(v,u)

, where

m^+(v,u)

counts directed edges from

v

u

, including loops where

u = v

and each loop (or multiplicity

m^+(v,v)

) contributes

m^+(v,v)

to the out-degree. Similarly, the in-degree

\deg^-(v) = \sum_{u \in V} m^-(u,v)

sums multiplicities of incoming edges, with loops contributing

m^-(v,v)

to the in-degree. The total degree is

\deg(v) = \deg^+(v) + \deg^-(v)

.^[26] The handshaking lemma extends naturally to multigraphs, maintaining its fundamental relation: in any undirected multigraph, the sum of all vertex degrees equals twice the number of edges,

\sum_{v \in V} \deg(v) = 2 |E|

, where

|E|

counts edges with multiplicity and each loop as one edge. This holds because each non-loop edge contributes 1 to two degrees and each loop contributes 2 to one degree.^[22] For directed multigraphs, the sum of out-degrees equals the sum of in-degrees, both equaling the total number of directed edges

|E|

.^[26]

Representations and Data Structures

Adjacency matrix adaptations

In the adjacency matrix representation of a multigraph, the standard adaptation replaces the binary 0/1 entries of a simple graph's matrix with the multiplicity of edges between vertices. Specifically, for an undirected multigraph

G

with vertex set

V = \{v_1, v_2, \dots, v_n\}

, the adjacency matrix

A_G = (a_{ij})

is an

n \times n

matrix where

a_{ij}

denotes the number of edges joining

v_i

and

v_j

.^[27] This matrix is symmetric (

A_G = A_G^T

) because the multiplicity is undirected. For loops, each loop at vertex

v_i

contributes 2 to the diagonal entry

a_{ii}

, reflecting its effect on the degree of

v_i

.^[27] For directed multigraphs (or multidigraphs), the adjacency matrix is non-symmetric, with

a_{ij}

representing the number of directed edges (arcs) from

v_i

v_j

.^[27] Loops in this case contribute 1 to the diagonal entry

a_{ii}

, as they are treated as arcs from a vertex to itself without the degree-doubling convention of undirected graphs. Consider an undirected multigraph with vertices labeled A, B, and C, where there are two edges between A and B, and one edge between B and C (no other edges or loops). The adjacency matrix, with rows and columns ordered A, B, C, is:

\begin{pmatrix} 0 & 2 & 0 \\ 2 & 0 & 1 \\ 0 & 1 & 0 \end{pmatrix}

020201010

This entry-wise multiplicity directly encodes the structure, allowing operations like matrix powers to count walks accounting for parallel edges.^[27] This representation is compact for dense multigraphs with high edge multiplicities, as it leverages the fixed $O(n^2)$ space to store all pairwise information without additional lists. However, it is space-inefficient for sparse multigraphs, where most entries are zero despite low overall edge counts, requiring $\Theta(n^2)$ storage compared to $\Theta(|E|)$ for list-based alternatives.^[28]

Incidence matrix for multigraphs

In graph theory, the incidence matrix of an undirected multigraph

G

with vertex set

V = \{v_1, \dots, v_n\}

and edge set

E = \{e_1, \dots, e_m\}

, where

m

counts each instance of multiple edges separately, is the

n \times m

matrix

M = [m_{ij}]

such that

m_{ij} = 1

v_i

is an endpoint of

e_j

(but not a loop),

m_{ij} = 2

e_j

is a loop at

v_i

, and

m_{ij} = 0

otherwise.^[17] This construction treats each parallel edge as a distinct column, resulting in identical columns for parallel edges sharing the same endpoints.^[29] For a directed multigraph, the incidence matrix is similarly an

n \times m

matrix with rows corresponding to vertices and columns to arcs (directed edges), where the entry is

+1

if the vertex is the tail of the arc,

-1

if it is the head, and

0

otherwise; parallel arcs receive separate columns, often yielding identical columns for arcs with the same tail-head pair.^[17] Loops in undirected multigraphs are handled by the entry of 2 in the corresponding row and column, reflecting the edge's incidence at the vertex twice, while in directed cases, a loop from a vertex to itself typically yields

+1

and

-1

in the same row, netting 0.^[17]^[30] Consider an undirected multigraph with vertices

A

and

B

, and two parallel edges

e_1

and

e_2

between them. The incidence matrix is the

2 \times 2

matrix

\begin{pmatrix} 1 & 1 \\ 1 & 1 \end{pmatrix},

where each column corresponds to one edge and is identical due to the parallels.^[29] This representation is particularly useful for edge-specific operations, such as defining the cycle space as the kernel of the incidence matrix in flow theory on multigraphs, though it becomes verbose when multiplicity is high due to the proliferation of repeated columns.^[31]^[17]

Applications and Examples

Modeling parallel connections in networks

In transportation networks, multiple edges between nodes representing cities or intersections can model parallel routes, such as alternative highways or lanes with varying travel times and costs.^[32] This approach is particularly useful in vehicle routing problems, where parallel edges capture different path options to optimize objectives like time or distance while adhering to constraints such as time windows.^[33] For instance, in a road network graph, an edge multiplicity

m(u,v) = 3

between nodes

u

and

v

might indicate three distinct highways, enabling detailed capacity analysis for traffic flow or emergency response planning.^[32] In communication networks, arcs with multiplicity represent parallel links or contacts between nodes, such as multiple transmission opportunities in satellite or delay-tolerant systems, where each edge encodes attributes like bandwidth capacity or duration.^[34] This modeling facilitates routing decisions that select compatible parallel connections to maximize throughput, as seen in contact multigraph routing for space networks, where multiple edges between nodes denote overlapping communication windows with specific data rates.^[34] In social networks, multiple edges between individuals capture diverse relational ties, such as friendship, professional collaboration, or familial bonds, allowing analysis of multiplex structures without reducing interactions to a single type.^[4] For example, in organizational studies, edges might represent simultaneous information exchange and financial transactions, revealing interdependencies like reciprocity across tie types.^[4] Multigraphs enable these applications by permitting multiple edges, which inherently support parallel connections in network models.^[33] A key benefit is capturing redundancy and distinct pathways—such as separate routes or ties—without relying on auxiliary weights that aggregate attributes, preserving the granularity needed for realistic analysis.^[32]

Role in graph algorithms

In shortest path algorithms like Dijkstra's, multiple edges between a pair of vertices are handled as distinct options, each contributing independently to the relaxation process based on their weights, enabling the selection of the optimal path among parallels. For efficiency in unweighted or uniformly weighted cases, implementations may preprocess by retaining only the minimum-weight edge between pairs, effectively reducing multiplicity without altering the result. ^[35] Regarding connectivity, multiple edges do not alter the fundamental connectedness of a graph—presence of at least one edge suffices for basic reachability—but they enhance edge-connectivity by increasing the minimum number of edges needed to disconnect vertices, thereby improving robustness against failures. ^[36] For Eulerian paths, the criteria in multigraphs mirror those in simple graphs: a connected multigraph has an Eulerian circuit if all vertices have even degree, and an Eulerian path if exactly zero or two vertices have odd degree, with multiplicity affecting degree counts but not the path's existence conditions. ^[37] In traversal algorithms such as BFS and DFS, multiple edges appear as repeated entries in adjacency lists, necessitating explicit tracking of used edges to prevent redundant traversals or to ensure complete edge coverage in applications like cycle detection or full exploration. ^[38] The inclusion of multiple edges inflates the edge set size |E|, elevating the time complexity of many graph algorithms from O(|V| + |E|) in simple graphs to higher bounds in dense multigraphs, particularly impacting naive implementations of traversal or flow-based methods. ^[39]

Info Pages

Talk Pages

Special Pages

Multiple edges

Recent from talks

Recent from talks

Contribute something

Contribute something

Media Pages

Timelines

Articles

Notes collections

Notes

Notes

Days in Chronicle

Multiple edges

Notes

References

Multiple edges

Definitions and Basic Concepts

Undirected multiple edges

Directed multiple edges

Multigraphs and Graph Types

Definition of multigraphs

Distinction from simple graphs

Properties and Measures

Edge multiplicity

Degree in the presence of multiple edges

Representations and Data Structures

Adjacency matrix adaptations

Incidence matrix for multigraphs

Applications and Examples

Modeling parallel connections in networks

Role in graph algorithms

References

Add your contribution

Related Hubs

Contribute something

History

Media collections

Multiple edges

Recent from talks

Recent from talks

Contribute something

Contribute something

Media Pages

Timelines

Articles

Notes collections

Notes

Notes

Days in Chronicle

Multiple edges

Notes

References

Multiple edges

Definitions and Basic Concepts

Undirected multiple edges

Directed multiple edges

Multigraphs and Graph Types

Definition of multigraphs

Distinction from simple graphs

Properties and Measures

Edge multiplicity

Degree in the presence of multiple edges

Representations and Data Structures

Adjacency matrix adaptations

Add your contribution

Related Hubs

Contribute something