Incidence matrix

Incidence matrix is a common graph representation in graph theory. It is different to an adjacency matrix, which encodes the relation of vertex-vertex pairs.

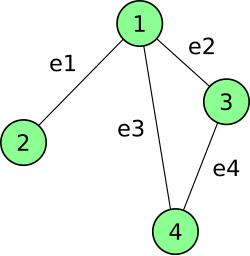
In graph theory an undirected graph has two kinds of incidence matrices: unoriented and oriented.

The unoriented incidence matrix (or simply incidence matrix) of an undirected graph is a ${\displaystyle n\times m}$ matrix B, where n and m are the numbers of vertices and edges respectively, such that

${\displaystyle B_{ij}=\left\{{\begin{array}{rl}\,1&{\text{if vertex }}v_{i}{\text{ is incident with edge }}e_{j},\\0&{\text{otherwise.}}\end{array}}\right.}$

For example, the incidence matrix of the undirected graph shown on the right is a matrix consisting of 4 rows (corresponding to the four vertices, 1–4) and 4 columns (corresponding to the four edges, ${\displaystyle e_{1},e_{2},e_{3},e_{4}}$):

If we look at the incidence matrix, we see that the sum of each column is equal to 2. This is because each edge has a vertex connected to each end.

The incidence matrix of a directed graph is a ${\displaystyle n\times m}$ matrix B where n and m are the number of vertices and edges respectively, such that

${\displaystyle B_{ij}=\left\{{\begin{array}{rl}{-1}&{\text{if edge }}e_{j}{\text{ leaves vertex }}v_{i},\\{\phantom {-}}1&{\text{if edge }}e_{j}{\text{ enters vertex }}v_{i},\\{\phantom {-}}0&{\text{otherwise.}}\end{array}}\right.}$

(Many authors use the opposite sign convention.)

The oriented incidence matrix of an undirected graph is the incidence matrix, in the sense of directed graphs, of any orientation of the graph. That is, in the column of edge e, there is one 1 in the row corresponding to one vertex of e and one −1 in the row corresponding to the other vertex of e, and all other rows have 0. The oriented incidence matrix is unique up to negation of any of the columns, since negating the entries of a column corresponds to reversing the orientation of an edge.

The unoriented incidence matrix of a graph G is related to the adjacency matrix of its line graph L(G) by the following theorem:

${\displaystyle A(L(G))=B(G)^{\textsf {T}}B(G)-2I_{m}.}$

where A(L(G)) is the adjacency matrix of the line graph of G, B(G) is the incidence matrix, and I_m is the identity matrix of dimension m.

The discrete Laplacian (or Kirchhoff matrix) is obtained from the oriented incidence matrix B(G) by the formula

${\displaystyle B(G)B(G)^{\textsf {T}}.}$

The integral cycle space of a graph is equal to the null space of its oriented incidence matrix, viewed as a matrix over the integers or real or complex numbers. The binary cycle space is the null space of its oriented or unoriented incidence matrix, viewed as a matrix over the two-element field.

The incidence matrix of a signed graph is a generalization of the oriented incidence matrix. It is the incidence matrix of any bidirected graph that orients the given signed graph. The column of a positive edge has a 1 in the row corresponding to one endpoint and a −1 in the row corresponding to the other endpoint, just like an edge in an ordinary (unsigned) graph. The column of a negative edge has either a 1 or a −1 in both rows. The line graph and Kirchhoff matrix properties generalize to signed graphs.

The definitions of incidence matrix apply to graphs with loops and multiple edges. The column of an oriented incidence matrix that corresponds to a loop is all zero, unless the graph is signed and the loop is negative; then the column is all zero except for ±2 in the row of its incident vertex.

A weighted graph can be represented using the weight of the edge in place of a 1. For example, the incidence matrix of the graph to the right is:

Because the edges of ordinary graphs can only have two vertices (one at each end), the column of an incidence matrix for graphs can only have two non-zero entries. By contrast, a hypergraph can have multiple vertices assigned to one edge; thus, a general matrix of non-negative integers describes a hypergraph.

The incidence matrix of an incidence structure C is a p × q matrix B (or its transpose), where p and q are the number of points and lines respectively, such that B_i,j = 1 if the point p_i and line L_j are incident and 0 otherwise. In this case, the incidence matrix is also a biadjacency matrix of the Levi graph of the structure. As there is a hypergraph for every Levi graph, and vice versa, the incidence matrix of an incidence structure describes a hypergraph.

An important example is a finite geometry. For instance, in a finite plane, X is the set of points and Y is the set of lines. In a finite geometry of higher dimension, X could be the set of points and Y could be the set of subspaces of dimension one less than the dimension of the entire space (hyperplanes); or, more generally, X could be the set of all subspaces of one dimension d and Y the set of all subspaces of another dimension e, with incidence defined as containment.

In a similar manner, the relationship between cells whose dimensions differ by one in a polytope, can be represented by an incidence matrix.^[1]

Another example is a block design. Here X is a finite set of "points" and Y is a class of subsets of X, called "blocks", subject to rules that depend on the type of design. The incidence matrix is an important tool in the theory of block designs. For instance, it can be used to prove Fisher's inequality, a fundamental theorem of balanced incomplete 2-designs (BIBDs), that the number of blocks is at least the number of points.^[2] Considering the blocks as a system of sets, the permanent of the incidence matrix is the number of systems of distinct representatives (SDRs).

• Parry–Sullivan invariant