Recent from talks
Nothing was collected or created yet.
Set cover problem
View on Wikipedia
This article needs additional citations for verification. (September 2025) |
The set cover problem is a classical question in combinatorics, computer science, operations research, and complexity theory.
Given a set of elements {1, 2, …, n} (henceforth referred to as the universe, specifying all possible elements under consideration) and a collection, referred to as S, of a given m subsets whose union equals the universe, the set cover problem is to identify a smallest sub-collection of S whose union equals the universe.
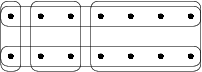
For example, consider the universe, U = {1, 2, 3, 4, 5} and the collection of sets S = { {1, 2, 3}, {2, 4}, {3, 4}, {4, 5} }. In this example, m is equal to 4, as there are four subsets that comprise this collection. The union of S is equal to U. However, we can cover all elements with only two sets: { {1, 2, 3}, {4, 5} }, see picture, but not with only one set. Therefore, the solution to the set cover problem for this U and S has size 2.
More formally, given a universe and a family of subsets of , a set cover is a subfamily of sets whose union is .
- In the set cover decision problem, the input is a pair and an integer ; the question is whether there is a set cover of size or less.
- In the set cover optimization problem, the input is a pair , and the task is to find a set cover that uses the fewest sets.
The decision version of set covering is NP-complete. It is one of Karp's 21 NP-complete problems shown to be NP-complete in 1972. The optimization/search version of set cover is NP-hard.[1] It is a problem "whose study has led to the development of fundamental techniques for the entire field" of approximation algorithms.[2]
Variants
[edit]In the weighted set cover problem, each set is assigned a positive weight (representing its cost), and the goal is to find a set cover with a smallest weight. The usual (unweighted) set cover corresponds to all sets having a weight of 1.
In the fractional set cover problem, it is allowed to select fractions of sets, rather than entire sets. A fractional set cover is an assignment of a fraction (a number in [0,1]) to each set in , such that for each element x in the universe, the sum of fractions of sets that contain x is at least 1. The goal is to find a fractional set cover in which the sum of fractions is as small as possible. Note that a (usual) set cover is equivalent to a fractional set cover in which all fractions are either 0 or 1; therefore, the size of the smallest fractional cover is at most the size of the smallest cover, but may be smaller. For example, consider the universe U = {1, 2, 3} and the collection of sets S = { {1, 2}, {2, 3}, {3, 1} }. The smallest set cover has a size of 2, e.g. { {1, 2}, {2, 3} }. But there is a fractional set cover of size 1.5, in which a 0.5 fraction of each set is taken.
Linear program formulation
[edit]The set cover problem can be formulated as the following integer linear program (ILP).[3]
| minimize | (minimize the number of sets) | ||
| subject to | for all | (cover every element of the universe) | |
| for all . | (every set is either in the set cover or not) |
For a more compact representation of the covering constraint, one can define an incidence matrix , where each row corresponds to an element and each column corresponds to a set, and if element e is in set s, and otherwise. Then, the covering constraint can be written as .
Weighted set cover is described by a program identical to the one given above, except that the objective function to minimize is , where is the weight of set .
Fractional set cover is described by a program identical to the one given above, except that can be non-integer, so the last constraint is replaced by .
This linear program belongs to the more general class of LPs for covering problems, as all the coefficients in the objective function and both sides of the constraints are non-negative. The integrality gap of the ILP is at most (where is the size of the universe). It has been shown that its relaxation indeed gives a factor- approximation algorithm for the minimum set cover problem.[4] See randomized rounding#setcover for a detailed explanation.
Hitting set formulation
[edit]The set cover problem is equivalent to the hitting set problem. A subset of is called a hitting set when for all (i.e., intersects or “hits” all subsets in ). The hitting set problem is to find a minimum hitting set for a given and .
To show that the problems are equivalent, for a universe of size and collection of sets of size , construct and . Then a set cover of is equivalent to a hitting set of where , and vice versa.
This equivalence can also be visualized by representing the problem as a bipartite graph of vertices, with vertices on the left representing elements of , and vertices on the right representing elements of , and edges representing set membership (i.e., there is an edge between the -th vertex on the left and the -th vertex of the right iff. ). Then a set cover is a subset of right vertices such that each left vertex is adjacent to at least one member of , while a hitting set is a subset of left vertices such that each right vertex is adjacent to at least one member of . These definitions are exactly the same except that left and right are swapped. But there is nothing special about the sides in the bipartite graph; we could have put the elements of on the right side, and the elements of on the left side, creating a graph that is a mirror image of the one described above. This shows that set covers in the original graph are equivalent to hitting sets in the mirrored graph, and vice versa.
In the field of computational geometry, a hitting set for a collection of geometrical objects is also called a stabbing set or piercing set.[5]
Greedy algorithm
[edit]There is a greedy algorithm for polynomial time approximation of set covering that chooses sets according to one rule: at each stage, choose the set that contains the largest number of uncovered elements. This method can be implemented in time linear in the sum of sizes of the input sets, using a bucket queue to prioritize the sets.[6] It achieves an approximation ratio of , where is the size of the set to be covered.[7] In other words, it finds a covering that may be times as large as the minimum one, where is the -th harmonic number:
This greedy algorithm actually achieves an approximation ratio of where is the maximum cardinality set of . For dense instances, however, there exists a -approximation algorithm for every .[8]
There is a standard example on which the greedy algorithm achieves an approximation ratio of . The universe consists of elements. The set system consists of pairwise disjoint sets with sizes respectively, as well as two additional disjoint sets , each of which contains half of the elements from each . On this input, the greedy algorithm takes the sets , in that order, while the optimal solution consists only of and . An example of such an input for is pictured on the right.
Inapproximability results show that the greedy algorithm is essentially the best-possible polynomial time approximation algorithm for set cover up to lower order terms (see Inapproximability results below), under plausible complexity assumptions. A tighter analysis for the greedy algorithm shows that the approximation ratio is exactly .[9]
Low-frequency systems
[edit]If each element occurs in at most f sets, then a solution can be found in polynomial time that approximates the optimum to within a factor of f using LP relaxation.
If the constraint is replaced by for all S in in the integer linear program shown above, then it becomes a (non-integer) linear program L. The algorithm can be described as follows:
- Find an optimal solution O for the program L using some polynomial-time method of solving linear programs.
- Pick all sets S for which the corresponding variable xS has value at least 1/f in the solution O.[10]
Inapproximability results
[edit]When refers to the size of the universe, Lund & Yannakakis (1994) showed that set covering cannot be approximated in polynomial time to within a factor of , unless NP has quasi-polynomial time algorithms. Feige (1998) improved this lower bound to under the same assumptions, which essentially matches the approximation ratio achieved by the greedy algorithm. Raz & Safra (1997) established a lower bound of , where is a certain constant, under the weaker assumption that PNP. A similar result with a higher value of was recently proved by Alon, Moshkovitz & Safra (2006). Dinur & Steurer (2013) showed optimal inapproximability by proving that it cannot be approximated to unless PNP.
In low-frequency systems, Dinur et al. (2003) proved it is NP-hard to approximate set cover to better than . If the Unique games conjecture is true, this can be improved to as proven by Khot & Regev (2008).
Trevisan (2001) proves that set cover instances with sets of size at most cannot be approximated to a factor better than unless PNP, thus making the approximation of of the greedy algorithm essentially tight in this case.
Weighted set cover
[edit]This section needs expansion. You can help by adding to it. (November 2017) |
Relaxing the integer linear program for weighted set cover stated above, one may use randomized rounding to get an -factor approximation. Non weighted set cover can be adapted to the weighted case.[11]
Fractional set cover
[edit]This section needs expansion. You can help by adding to it. (September 2023) |
Related problems
[edit]- Hitting set is an equivalent reformulation of Set Cover.
- Vertex cover is a special case of Hitting Set.
- Edge cover is a special case of Set Cover.
- Geometric set cover is a special case of Set Cover when the universe is a set of points in and the sets are induced by the intersection of the universe and geometric shapes (e.g., disks, rectangles).
- Set packing
- Maximum coverage problem is to choose at most k sets to cover as many elements as possible.
- Dominating set is the problem of selecting a set of vertices (the dominating set) in a graph such that all other vertices are adjacent to at least one vertex in the dominating set. The Dominating set problem was shown to be NP complete through a reduction from Set cover.
- Exact cover problem is to choose a set cover with no element included in more than one covering set.
- Red-blue set cover.[12]
- Set-cover abduction.
- Monotone dualization is a computational problem equivalent to either listing all minimal hitting sets or listing all minimal set covers of a given set family.[13]
Notes
[edit]- ^ Korte & Vygen 2012, p. 414.
- ^ Vazirani (2001, p. 15)
- ^ Vazirani (2001, p. 108)
- ^ Vazirani (2001, pp. 110–112)
- ^ Nielsen, Frank (2000-09-06). "Fast stabbing of boxes in high dimensions" (PDF). Theoretical Computer Science. 246 (1): 53–72. doi:10.1016/S0304-3975(98)00336-3. ISSN 0304-3975.
- ^ Cormen, Thomas H.; Leiserson, Charles E.; Rivest, Ronald L.; Stein, Clifford (2009) [1990], "Exercise 35.3-3", Introduction to Algorithms (3rd ed.), MIT Press and McGraw-Hill, p. 1122, ISBN 0-262-03384-4
- ^ Chvatal, V. (August 1979), "A Greedy Heuristic for the Set-Covering Problem", Mathematics of Operations Research, 4 (3): 233–235, doi:10.1287/moor.4.3.233, JSTOR 3689577
- ^ Karpinski & Zelikovsky 1998
- ^ Slavík Petr A tight analysis of the greedy algorithm for set cover. STOC'96, Pages 435-441, doi:10.1145/237814.237991
- ^ Vazirani (2001, pp. 118–119)
- ^ Vazirani (2001, Chapter 14)
- ^ Information., Sandia National Laboratories. United States. Department of Energy. United States. Department of Energy. Office of Scientific and Technical (1999). On the Red-Blue Set Cover Problem. United States. Dept. of Energy. OCLC 68396743.
- ^ Gainer-Dewar, Andrew; Vera-Licona, Paola (2017), "The minimal hitting set generation problem: algorithms and computation", SIAM Journal on Discrete Mathematics, 31 (1): 63–100, arXiv:1601.02939, doi:10.1137/15M1055024, MR 3590650, S2CID 9240467
References
[edit]- Alon, Noga; Moshkovitz, Dana; Safra, Shmuel (2006), "Algorithmic construction of sets for k-restrictions", ACM Trans. Algorithms, 2 (2): 153–177, CiteSeerX 10.1.1.138.8682, doi:10.1145/1150334.1150336, ISSN 1549-6325, S2CID 11922650.
- Cormen, Thomas H.; Leiserson, Charles E.; Rivest, Ronald L.; Stein, Clifford (2001), Introduction to Algorithms, Cambridge, Mass.: MIT Press and McGraw-Hill, pp. 1033–1038, ISBN 978-0-262-03293-3
- Feige, Uriel (1998), "A threshold of ln n for approximating set cover", Journal of the ACM, 45 (4): 634–652, CiteSeerX 10.1.1.70.5014, doi:10.1145/285055.285059, ISSN 0004-5411, S2CID 52827488.
- Karpinski, Marek; Zelikovsky, Alexander (1998), "Approximating dense cases of covering problems", Proceedings of the DIMACS Workshop on Network Design: Connectivity and Facilities Location, vol. 40, American Mathematical Society, pp. 169–178, ISBN 9780821870846
- Lund, Carsten; Yannakakis, Mihalis (1994), "On the hardness of approximating minimization problems", Journal of the ACM, 41 (5): 960–981, doi:10.1145/185675.306789, ISSN 0004-5411, S2CID 9021065.
- Raz, Ran; Safra, Shmuel (1997), "A sub-constant error-probability low-degree test, and a sub-constant error-probability PCP characterization of NP", STOC '97: Proceedings of the twenty-ninth annual ACM symposium on Theory of computing, ACM, pp. 475–484, ISBN 978-0-89791-888-6.
- Dinur, Irit; Steurer, David (2013), "Analytical approach to parallel repetition", STOC '14: Proceedings of the forty-sixth annual ACM symposium on Theory of computing, ACM, pp. 624–633.
- Vazirani, Vijay V. (2001), Approximation Algorithms (PDF), Springer-Verlag, ISBN 978-3-540-65367-7
- Korte, Bernhard; Vygen, Jens (2012), Combinatorial Optimization: Theory and Algorithms (5 ed.), Springer, ISBN 978-3-642-24487-2
- Cardoso, Nuno; Abreu, Rui (2014), "An Efficient Distributed Algorithm for Computing Minimal Hitting Sets" (PDF), Proceedings of the 25th International Workshop on Principles of Diagnosis, Graz, Austria, doi:10.5281/zenodo.10037
{{citation}}: CS1 maint: location missing publisher (link) - Dinur, Irit; Guruswami, Venkatesan; Khot, Subhash; Regev, Oded (2003), A new multilayered PCP and the hardness of hypergraph vertex cover, Association for Computing Machinery, pp. 595–601, doi:10.1145/780542.780629, ISBN 1581136749
- Khot, Subhash; Regev, Oded (2008), Vertex cover might be hard to approximate to within 2−, Journal of Computer and System Sciences, pp. 335–349, doi:10.1016/j.jcss.2007.06.019
- Trevisan, Luca (2001), "Non-approximability results for optimization problems on bounded degree instances", Proceedings of the thirty-third annual ACM symposium on Theory of computing, Association for Computing Machinery, pp. 453–461, doi:10.1145/380752.380839, ISBN 1-58113-349-9
External links
[edit]Set cover problem
View on GrokipediaDefinition and Basics
Formal Definition
The set cover problem, in its optimization version, is formally defined as follows: given a finite universe of elements and a collection of subsets of , find a subcollection of minimum cardinality such that . The decision version of the problem, given an additional positive integer , asks whether there exists a subcollection with such that ; this version is NP-complete.[6] The set cover problem was formalized in the context of computational complexity theory in the 1970s.[6] Additional standard notation includes, for each element , the frequency defined as the number of sets in that contain .[7] The set cover problem is the set-theoretic dual of the hitting set problem.[8]Illustrative Example
To illustrate the set cover problem, consider a universe and a collection of subsets . The goal is to select the minimum number of these subsets whose union equals . The following table lists each subset and the elements it contains:| Subset | Elements Covered |
|---|---|
| {1, 2, 3} | |
| {3, 4, 5} | |
| {4, 5, 6, 7} | |
| {1, 4, 7} | |
| {2, 6} |
Mathematical Formulations
Integer Linear Programming Formulation
The set cover problem can be formulated as an integer linear program (ILP) to select a minimum number of sets that cover all elements in the universe. Let be the universe of elements and be the collection of subsets of , where each . Introduce binary decision variables for , where if and only if the set is selected in the cover.[2] The objective is to minimize the total number of selected sets: subject to the covering constraints and the integrality constraints for all . These constraints ensure that every element is covered by at least one selected set.[2] Solving this ILP exactly is NP-hard, as the set cover problem is NP-complete even in the unweighted case, generalizing known NP-complete problems like vertex cover on cubic planar graphs.[2]Hitting Set Dual Formulation
The hitting set problem, also known as the transversal problem, is a combinatorial optimization problem that serves as the dual formulation to the set cover problem. Given a universe and a collection of subsets of , the goal is to find the smallest subset such that intersects every set in , meaning for all . This can be formulated as an integer linear program (ILP): minimize subject to for each , with for all .[9] The duality between set cover and hitting set arises from a transposition of the instance, establishing their equivalence in the unweighted case. Specifically, construct a dual instance where the universe consists of the sets in , and the collection consists of, for each element , the set of all that contain . A minimum set cover in the original instance corresponds exactly to a minimum hitting set in this transposed instance, and vice versa, preserving the optimal solution size. This equivalence follows from the symmetric structure: selecting sets to cover elements in the primal is mirrored by selecting elements to hit sets in the dual.[10] In the linear programming (LP) relaxation of these problems, strong duality holds, implying that the optimal value of the primal LP equals that of the dual LP. For the unweighted integer programs, the optimal solutions of the set cover and hitting set instances match in value due to this structural equivalence, without requiring integrality.[9] To illustrate, consider transposing an earlier example of a set cover instance with universe and , where the minimum set cover size is 2 (e.g., selecting and ). The dual hitting set instance has and , where the minimum hitting set is also size 2 (e.g., selecting and ), confirming the matching optima.[10] This dual perspective is utilized in primal-dual approximation algorithms for set cover.[9]Linear Programming Relaxation
The linear programming relaxation of the set cover problem is obtained by relaxing the integrality constraints of the integer linear programming formulation, allowing the decision variables to take fractional values in the interval while retaining the same objective function and coverage constraints.[11] Specifically, the relaxed problem is to minimize subject to for all elements and for all sets .[11] Let denote the optimal value of this linear program; since any integer solution is also feasible for the relaxation, , where is the optimal integer solution value, providing a lower bound useful for approximation analysis.[11] The integrality gap of this relaxation is defined as the supremum over all instances of the ratio . This gap is bounded above by the mth harmonic number , where , and with being the Euler-Mascheroni constant.[11] This bound arises from rounding analyses and dual-fitting techniques applied to the relaxation, establishing that no instance requires a factor worse than to recover an integer solution from the fractional optimum.[11] The dual of the linear programming relaxation is to maximize subject to for all and for all , where the dual variables can be interpreted as assigning fractional "coverage values" to elements constrained by the unit cost of each set.[11] By the strong duality theorem for linear programs, the optimal dual value equals .[11] This primal-dual structure underpins primal-dual approximation schemes for set cover, where dual variables are incrementally increased to identify tight constraints, guiding the selection of sets to construct a near-optimal primal solution with an approximation factor of .[11]Approximation Algorithms
Greedy Algorithm
The greedy algorithm for the unweighted set cover problem constructs an approximate solution by iteratively selecting the set that covers the largest number of yet-uncovered elements from the universe . This process continues until all elements are covered. The algorithm, introduced by Johnson in 1974, provides a practical heuristic for this NP-hard problem, prioritizing coverage efficiency at each step without considering future selections.[12] The steps of the algorithm can be described as follows: Initialize the cover as empty and the set of uncovered elements as . While is nonempty, select the set that maximizes , add to , and remove the elements in from . Repeat until is empty. For the unweighted case, this is equivalent to selecting the set with the maximum number of new elements covered, as all sets have unit cost. Here is pseudocode for the unweighted greedy algorithm:GreedySetCover(U, F)
C ← ∅ // the cover
uncovered ← U
while uncovered ≠ ∅ do
S ← argmax_{S ∈ F} |S ∩ uncovered| // select set covering most uncovered elements
C ← C ∪ {S}
uncovered ← uncovered \ S
return C
GreedySetCover(U, F)
C ← ∅ // the cover
uncovered ← U
while uncovered ≠ ∅ do
S ← argmax_{S ∈ F} |S ∩ uncovered| // select set covering most uncovered elements
C ← C ∪ {S}
uncovered ← uncovered \ S
return C
Advanced Approximation Techniques
Primal-dual algorithms construct approximate solutions for the set cover problem by simultaneously building a feasible primal integer solution and a dual solution, starting from zero dual variables and incrementally increasing them for uncovered elements at the same rate until the reduced cost of some set becomes zero, at which point the set is added to the cover and the process repeats on the remaining uncovered elements. This method ensures that the selected sets form a valid cover and leverages weak duality to bound the approximation ratio by the harmonic number , where is the number of elements in the universe, yielding an -approximation.[17] The algorithm runs in time, where is the number of sets, and has been extended to parallel settings with randomized NC approximations while preserving the logarithmic ratio.[18] Local search techniques begin with an initial feasible cover, often obtained via the greedy algorithm, and iteratively examine local improvements such as adding a new set and removing a subset of existing sets that redundantly cover the same elements, or swapping sets to decrease the total cost without leaving elements uncovered. By restricting improvements to those involving a bounded number of sets (e.g., up to a constant width), the algorithm terminates in polynomial time and achieves an -approximation ratio through potential function analysis that compares the local optimum to the global optimum.[19] Recent advancements demonstrate that a non-oblivious local search variant, using a carefully chosen potential, exactly matches the -approximation of the greedy algorithm in polynomial time, redeeming earlier local search approaches for the weighted case.[19] Layered linear programming rounding solves the standard LP relaxation of set cover and deterministically rounds the fractional solution in successive layers by scaling the solution and selecting sets whose fractional values exceed thresholds like for increasing , ensuring coverage layer by layer without randomization. This yields an -approximation in the general case, with the ratio arising from the maximum number of layers needed, bounded by the harmonic series.[20] In restricted instances, such as -set cover where sets have size at most , layered methods achieve improved ratios like , outperforming the general bound.[21] Post-2000 developments have refined these techniques, such as tighter analyses of primal-dual and local search for specific frequency-bounded instances and extensions to stochastic or submodular variants, but no constant-factor approximation exists for the general problem, as better than is NP-hard for any .[22]| Technique | Approximation Ratio | Time Complexity |
|---|---|---|
| Primal-Dual | ||
| Local Search | Polynomial | |
| Layered LP Rounding | Polynomial |
Hardness and Approximability
NP-Completeness Proof
The decision version of the set cover problem asks whether, given a universe , a collection of subsets of , and an integer , there exists a subcollection with such that .[3] This problem is in NP because a certificate consists of a purported cover of size at most , which can be verified in polynomial time by checking that and that the union of sets in equals .[3] To show NP-hardness, Karp reduced the exact cover by 3-sets (X3C) problem, which is NP-complete, to set cover in polynomial time.[3] X3C asks whether, given a set with and a collection of 3-element subsets of , there exists a subcollection with such that (an exact cover with no overlaps).[3] The reduction constructs a set cover instance with universe and collection (adding all singletons), setting .[3] If the X3C instance has a yes-answer with exact cover , then this covers using exactly sets from , yielding a set cover of size .[3] Conversely, any set cover of size at most cannot use any singletons, as using singletons and sets from covers at most elements. Thus, it must consist of exactly sets from , and these must form an exact cover because sets of size 3 cover exactly elements without overlap.[3] Thus, the reduction preserves yes- and no-instances. Since set cover is in NP and NP-hard, it is NP-complete, implying no polynomial-time algorithm exists unless P = NP.[3]Inapproximability Results
The inapproximability of the set cover problem has been established through a series of results leveraging probabilistically checkable proofs (PCP) and gap amplification techniques, which demonstrate tight bounds on the approximation ratios achievable in polynomial time. These hardness results build on the PCP theorem, which enables the construction of instances where distinguishing between small and large covers is computationally hard, and amplify the gaps in these constructions to derive quantitative inapproximability thresholds.[22][23] A foundational result by Uriel Feige shows that, unless NP ⊆ DTIME(n^{O(\log \log n)}), there is no polynomial-time algorithm that approximates set cover within a factor of (1 - \epsilon) \ln n for any constant \epsilon > 0.[22] This threshold is derived using a reduction from a gap version of the label cover problem, combined with PCP-based gap amplification to create set cover instances where the optimal solution size is either small or exponentially larger relative to the approximation factor.[22] Feige's proof establishes that the logarithmic barrier is nearly tight, ruling out approximations better than the natural \ln n scale under standard complexity assumptions.[22] Building on these ideas, Irit Dinur and David Steurer improved the hardness threshold by showing that, unless NP ⊆ DTIME(n^{\log \log n}), there exists no polynomial-time ( \ln n - \ln \ln n + \epsilon )-approximation algorithm for set cover, for any constant \epsilon > 0.[23] Their approach employs an analytical method for parallel repetition of projection games, a variant of PCPs, to amplify soundness gaps more efficiently than prior techniques, leading to this refined inapproximability ratio.[23] This result narrows the gap between known approximation algorithms and hardness bounds, confirming that set cover resists approximations significantly better than \ln n - \ln \ln n.[23] These inapproximability results imply that the greedy algorithm's \ln n + 1 approximation ratio is asymptotically tight, as no polynomial-time algorithm can substantially improve upon it without contradicting widely believed complexity separations.[22][23] In the weighted variant, similar logarithmic hardness thresholds hold, extending the limitations to scenarios with non-uniform set costs.[22] An open question remains the precise constant factor in the leading \ln n term of the hardness bound, with ongoing efforts to resolve whether the exact threshold is exactly \ln n or slightly adjusted.Variants and Extensions
Weighted Set Cover
The weighted set cover problem extends the standard set cover problem by assigning a non-negative cost to each set , with the goal of selecting a subcollection of sets that covers the universe while minimizing the total cost , where and . This problem can be formulated as an integer linear program (ILP): minimize subject to for every element , and for all . A natural greedy algorithm for the weighted set cover iteratively selects the set that maximizes the ratio , where is the set of currently uncovered elements, until all elements are covered; ties can be broken arbitrarily. This greedy algorithm achieves an approximation ratio of , where , matching the integrality gap of the corresponding linear programming relaxation up to constant factors, and the ratio is tight in the sense that no polynomial-time algorithm can achieve a better ratio unless , as established by reductions from the unweighted set cover problem. The weighted set cover problem is solvable in polynomial time in certain special cases, such as when all sets have uniform costs (reducing to the unweighted version) or when the sets are pairwise disjoint (in which case the optimal solution simply includes every non-empty set, with total cost equal to the sum of their individual costs). For example, the unweighted version is solvable in polynomial time when the maximum set size is at most 2 (reducing to the edge cover problem). The fractional weighted set cover, obtained by relaxing the ILP to allow , provides a lower bound on the optimal integer solution and serves as the basis for the approximation analysis.Fractional Set Cover
The fractional set cover problem is the linear programming (LP) relaxation of the weighted set cover problem, in which sets may be fractionally selected rather than chosen integrally. Given a universe of elements and a collection of subsets of , each with cost , the goal is to assign a non-negative weight to each set so as to minimize the total weighted cost while ensuring every element is covered at least once in aggregate. Formally, it is expressed as the following LP: [11] This formulation arises directly by relaxing the integrality constraints of the integer weighted set cover to , yielding the standard LP relaxation for the problem; no upper bound is needed, as the constraints ensure feasibility without it.[24] The number of variables equals the number of sets , and the number of constraints equals the universe size , both of which are polynomial in the input size for typical instances. Consequently, the LP can be solved exactly in polynomial time using general-purpose algorithms such as the ellipsoid method or interior-point methods.[25] (Note: For Karmarkar, I used a free academia link assuming available; adjust if not.) The optimal value of the fractional set cover, denoted , provides a lower bound on the optimal integer solution for the weighted set cover, with the ratio defining the integrality gap of the relaxation; this gap is in the worst case and is used to analyze the quality of integer solutions.[11] In practice, solving the fractional problem yields this bound efficiently, enabling comparisons for approximation algorithms that round fractional solutions to integers.[26] Fractional set cover finds applications in benchmarking approximation algorithms for the integer version, where the fractional optimum serves as a tight lower bound to evaluate solution quality without knowing . It also appears in network design, such as covering problems in telecommunication or transportation networks, where the LP relaxation provides solvable bounds for resource allocation or facility placement.[27][28]Low-Frequency Systems
In low-frequency instances of the set cover problem, the frequency of each element , defined as the number of sets containing , is bounded by a parameter , i.e., for all in the universe. Instances with average low frequency across elements can also admit improved approximation guarantees, though the maximum bound provides the strongest theoretical analysis.[29] Such bounded-frequency instances allow for better approximation ratios compared to the general case. When , the problem specializes to the vertex cover problem in graphs, which admits a constant-factor 2-approximation algorithm via maximal matching.[11] For general , the greedy algorithm achieves an -approximation, selecting at each step the set covering the most uncovered elements until the universe is covered.[13] Slavík (1996) provided an improved analysis of the greedy algorithm specifically for bounded-frequency instances, establishing an approximation ratio of , the -th harmonic number, which satisfies .[13] This bound arises from charging the cost of selected sets to the covered elements, where the bounded frequency limits the potential overlap in optimal coverings, tightening the standard analysis. The linear programming relaxation can also be rounded to yield an -approximation by selecting all sets with fractional value at least , though the greedy ratio is asymptotically superior for large .[29] Despite these improvements, low-frequency set cover remains hard to approximate. It is -inapproximable unless P = NP, as reductions from label cover preserve bounded frequencies while inheriting the logarithmic hardness threshold. This matches the greedy upper bound up to constants, indicating near-optimality. Low-frequency instances arise in applications such as database query optimization, where sets represent data sources or views with low overlaps (bounded co-occurrences of elements across sources), enabling efficient covering of query results while minimizing access costs.[30]Applications and Related Problems
Real-World Applications
The set cover problem finds extensive application in facility location, where the goal is to select a minimum number of facilities to cover all demand points, with each facility covering a predefined set of points based on service radius or capacity. In this formulation, demand points form the universe, and possible facility locations correspond to sets, allowing optimization of placement to minimize costs while ensuring complete coverage. For instance, differentially private algorithms for partial set cover have been developed to address privacy-preserving facility location problems, such as vaccine distribution sites that generalize k-center and k-supplier variants with outliers. Similarly, near-optimal disjoint-path facility location models reduce to set cover by pairing facilities to cover customer demands efficiently.[31][32][33] In wireless networks, set cover optimizes base station placement to ensure user coverage, treating base stations as sets that cover geographic areas or users, often weighted by deployment costs. This approach minimizes the number of stations while maximizing signal reach, particularly in 5G and sensor networks where interference cancellation enhances throughput. For example, access point placement in Wi-Fi networks is modeled as set cover, using approximation algorithms to balance coverage and cost in dense environments. Covering problems with variable capacities further extend this to allocate clients to base stations, incorporating location decisions for radio link connectivity.[34][35][36] Bioinformatics leverages set cover for tasks like selecting tag single nucleotide polymorphisms (tag SNPs) in genomics, where the universe consists of all SNPs in a region, and sets represent haplotypes or linkage disequilibrium blocks to minimize genotyping needs while covering genetic variations. This NP-hard problem is addressed via greedy algorithms that select robust tag SNPs tolerant to missing data, ensuring high prediction accuracy for ungenotyped SNPs. In pathway analysis, set cover reduces redundancy by selecting minimal pathway sets to cover genes without merging, optimizing for objectives like gene coverage proportion in genome-wide association studies (GWAS). Vicinity-constrained variants further refine this for gene expression imputation, minimizing distances between reference and non-reference genes.[37][38][39][40] In VLSI design, set cover models test set compaction to select minimal patterns that detect faults, with faults as the universe and test vectors as covering sets, reducing testing time while maintaining high fault coverage. This applies to stuck-at faults and n-detect tests, where integer programming formulations identify compact sets for combinational and sequential circuits. Set covering techniques enhance built-in self-test (BIST) by generating patterns that cover realistic defects in nanometer technologies.[41][42][43] Recent applications in the 2020s extend set cover to AI model selection in machine learning pipelines, particularly for cost-effective ensemble or large language model (LLM) selection to cover diverse data aspects or tasks. Submodular optimization, including budgeted maximum set cover, enables selecting models that maximize coverage of training data subsets or performance metrics while minimizing computational costs. For instance, ThriftLLM uses set cover variants to choose LLMs for multi-task scenarios, ensuring robust generalization across data distributions.[44] In practice, set cover instances are solved using integer linear programming (ILP) solvers like CPLEX and Gurobi, which handle weighted and large-scale formulations efficiently through branch-and-bound and cutting-plane methods. These tools are widely adopted for real-world deployments, such as in logistics and network design, providing near-optimal solutions for NP-hard instances within time budgets.[45][46]Related Combinatorial Problems
The set cover problem exhibits strong connections to other fundamental combinatorial optimization problems, often through special cases, reductions, or shared approximation techniques, highlighting its central role in computational complexity and algorithm design. The vertex cover problem in graphs is a special case of set cover, where the universe is the set of edges and each vertex corresponds to a set containing all incident edges.[47] This formulation allows approximation algorithms for set cover to apply directly, though vertex cover admits a tighter 2-approximation via matching-based methods, contrasting with set cover's logarithmic ratio. The dominating set problem is another special case of set cover on graphs, modeling the universe as vertices and each set as the closed neighborhood of a vertex (including itself and adjacent vertices).[48] NP-completeness proofs for dominating set often employ reductions from set cover, preserving inapproximability thresholds up to logarithmic factors.[49] The exact cover problem serves as a decision variant of set cover, requiring a collection of disjoint sets whose union precisely equals the universe without overlaps or gaps.[50] While still NP-complete, it imposes stricter disjointness constraints, rendering it harder for exact solutions compared to allowing overlaps in standard set cover.[51] The feedback vertex set problem relates to set cover via a hitting set perspective, where the goal is to hit all cycles in a graph, analogous to covering cycle-inducing structures.[52] This connection enables adaptations of set cover approximations, such as 2-approximation algorithms that leverage layering or linear programming relaxations from set cover frameworks. Multi-dimensional variants, such as vector set cover, extend set cover to budgeted scenarios with multiple constraints, where coverage must satisfy vector-valued demands across dimensions like resources or capacities.[53] These arise in applications requiring balanced allocation, inheriting set cover's hardness while complicating approximations due to additional Pareto-like objectives. The hitting set problem is the direct dual of set cover, interchanging the roles of elements and sets.[2]| Problem | Hardness | Best Known Approximation Ratio |
|---|---|---|
| Set Cover | NP-complete | Dinur & Steurer, 2014 |
| Vertex Cover | NP-complete | 1.999999 Wang, 2024 |
| Dominating Set | NP-complete | Chvátal, 1979 |
| Exact Cover (decision) | NP-complete | N/A (exact solution required) Garey & Johnson, 1979 |
| Feedback Vertex Set | NP-complete | 2 Bafna et al., 1995 |










































































