Community hub
0 subscribers8 pages, 0 posts
Recent from talks
All channels
Be the first to start a discussion here.
Be the first to start a discussion here.
Be the first to start a discussion here.
Be the first to start a discussion here.
Contribute something
Welcome to the community hub built to collect knowledge and have discussions related to Axial parallelism.
Nothing was collected or created yet.
Axial parallelism
View on Wikipediafrom Wikipedia
Axial parallelism (also called gyroscopic stiffness, gyroscopic inertia, gyroscopic rigidity, or "rigidity in space") is the characteristic of a rotating body in which the direction of the axis of rotation remains fixed as the object moves through space. In astronomy, this characteristic is found in astronomical bodies in orbit. It is the same effect that causes a gyroscope's axis of rotation to remain constant as Earth rotates, allowing the devices to measure Earth's rotation.[1]
Examples
[edit]Earth's axial parallelism
[edit]
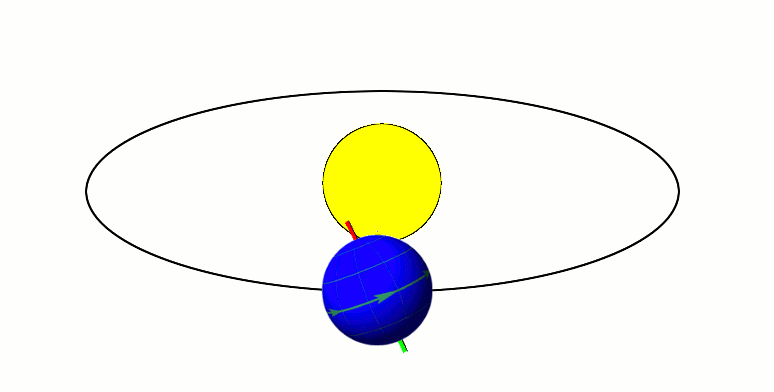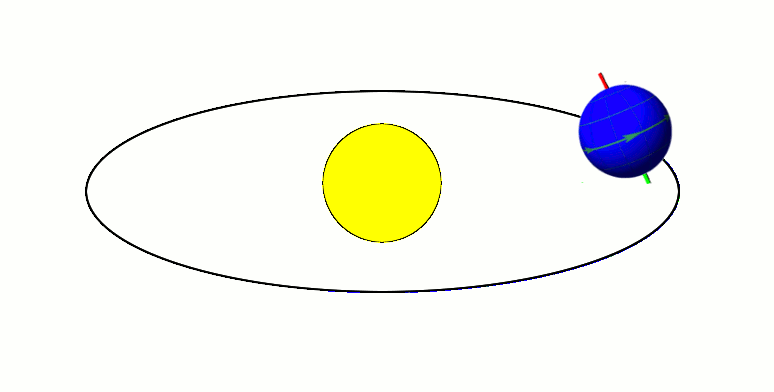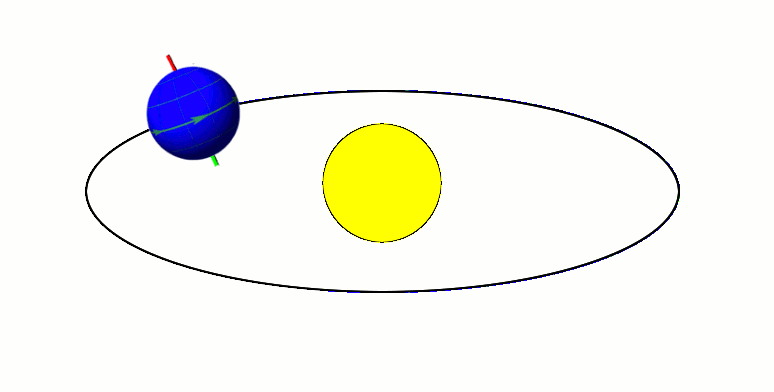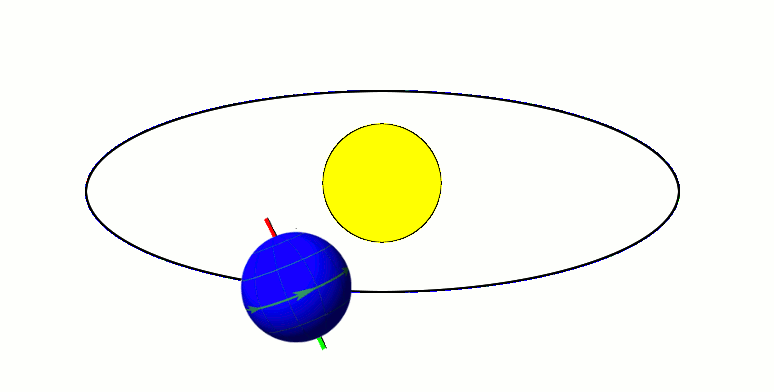
The Earth's orbit, with its axis tilted at 23.5 degrees, exhibits approximate axial parallelism, maintaining its direction towards Polaris (the "North Star") year-round. Together with the Earth's axial tilt, this is one of the primary reasons for the Earth's seasons, as illustrated by the diagram to the right.[2][3][4][5] It is also the reason that the stars appear fixed in the night sky, such as a "fixed" pole star, throughout Earth's orbit around the Sun.[6]
Minor variation in the direction of the axis, known as axial precession, takes place over the course of 26,000 years. As a result, over the next 11,000 years the Earth's axis will move to point towards Vega instead of Polaris.[7]
Other astronomical examples
[edit].jpg)
Axial parallelism is widely observed in astronomy. For example, the axial parallelism of the Moon's orbital plane[8] is a key factor in the phenomenon of eclipses. The Moon's orbital axis precesses a full circle during the 18 year, 10 day saros cycle. When the Moon's orbital tilt is aligned with the ecliptic tilt, it is 29 degrees from the ecliptic, while when they are anti-aligned (9 years later), the orbital inclination is only 18 degrees.
In addition, the rings of Saturn remain in a fixed direction as that planet rotates around the Sun.[9]
Explanation
[edit]Early gyroscopes were used to demonstrate the principle, most notably the Foucault's gyroscope experiment.[10] Prior to the invention of the gyroscope, it had been explained by scientists in various ways.[9] Early modern astronomer David Gregory, a contemporary of Isaac Newton, wrote:
To explain the Motion of the Celestial Bodies about their proper Axes, given in Position, and the Revolutions of them… If a Body be said to be moved about a given Axe, being in other respects not moved, that Axe is suppos'd to be unmov'd, and every point out of it to describe a Circle, to whose Plane the Axis is perpendicular. And for that reason, if a Body be carried along a line, and at the same time be revolved about a given Axe; the Axe, in all the time of the Body's motion, will continue parallel to it self. Nor is any thing else required to preserve this Parallelism, than that no other Motion besides these two be impressed upon the Body; for if there be no other third Motion in it, its Axe will continue always parallel to the Right-line, to which it was once parallel.[11]
This gyroscopic effect is described in modern times as "gyroscopic stiffness" or "rigidity in space". The Newtonian mechanical explanation is known as the conservation of angular momentum.[12]
See also
[edit]References
[edit]- ^ Kumar, B.; DeRemer, D.; Marshall, D. (2005). An Illustrated Dictionary of Aviation. McGraw-Hill Education. p. 326. ISBN 978-0-07-139606-6. Retrieved 2022-12-03.
Because of rigidity in space, a gyroscope does not tilt its axis of rotation as the earth rotates.
- ^ Petersen, J.; Sack, D.; Gabler, R.E. (2014). Fundamentals of Physical Geography. Cengage Learning. p. 18. ISBN 978-1-285-96971-8. Retrieved 2022-12-02.
- ^ The Popular Educator. John Cassell. 1856. p. 89. Retrieved 2022-12-02.
- ^ Oliver, J.E. (2008). Encyclopedia of World Climatology. Springer Netherlands. p. 651. ISBN 978-1-4020-3264-6. Retrieved 2022-12-02.
- ^ Rohli, R.V.; Vega, A.J. (2011). Climatology. Jones & Bartlett Learning, LLC. p. 30. ISBN 978-1-4496-5591-4. Retrieved 2022-12-02.
- ^ Lerner, K. Lee; Lerner, Brenda Wilmoth (2003). World of earth science. Farmington Hills, MI: Thomson-Gale. p. 487. ISBN 0-7876-9332-4. OCLC 60695883.
Although these distances seem counterintuitive to residents of the Northern Hemisphere who experience summer in July and winter in January—the seasons are not nearly as greatly affected by distance as they are by changes in solar illumination caused by the fact that Earth's polar axis is inclined 23.5 degrees from the perpendicular to the ecliptic (the plane of the solar system through or near which most of the planet's orbits travel) and because the Earth exhibits parallelism (currently toward Polaris, the North Star) as it revolves about the Sun.
- ^ Lerner, K. Lee; Lerner, Brenda Wilmoth (2003). World of earth science. Farmington Hills, MI: Thomson-Gale. p. 105 and 454. ISBN 0-7876-9332-4. OCLC 60695883.
During revolution about the Sun, the earth's polar axis exhibits parallelism to Polaris (also known as the North Star). Although observing parallelism, the orientation of Earth's polar axis exhibits precession—a circular wobbling exhibited by gyroscopes—that results in a 28,000-year-long precessional cycle. Currently, Earth's polar axis points roughly in the direction of Polaris (the North Star). As a result of precession, over the next 11,000 years, Earth's axis will precess or wobble so that it assumes an orientation toward the star Vega.
- ^ Gravesande, W.J.; Desaguliers, J.T.; Newton, I. (1726). Mathematical Elements of Natural Philosophy Confirmed by Experiments, Or An Introduction to Sir Isaac Newton's Philosophy ... Translated Into English by J. T. Desaguliers ... The Second Edition, Carefully Review'd and Corrected by the Translator. p. 184. Retrieved 2022-12-03.
The Axis of the Moon is not perpendicular to the Plane of its Orbit, but a little inclin'd to it: The Axis keeps its Parallelism in its Motion round the Earth
- ^ a b Ferguson, J. (1673). Astronomy Explained Upon Sir Isaac Newton's Principles ... A New Edition, Corrected. [With Plates.]. W. Strahan. p. 189. Retrieved 2022-12-02.
- ^ The Encyclopaedia Britannica: A Dictionary of Arts, Sciences and General Literature. R.S. Peale. 1890. p. 351. Retrieved 2022-12-02.
Under the title of precession instruments, various pieces of apparatus, involving the gyroscope principle, have been in use for a number of years for illustrating the precession of the equinoxes, and the parallelism of the earth's axis as it revolves round the sun.
- ^ Gregory, D. (1715). The Elements of Astronomy, Physical and Geometrical. By David Gregory ... Done Into English, with Additions and Corrections. To which is Annex'd, Dr. Halley's Synopsis of the Astronomy of Comets . J. Nicholson ... sold. p. 59. Retrieved 2022-12-02.
- ^ Giordano, N. (2012). College Physics: Reasoning and Relationships. Cengage Learning. p. 299. ISBN 978-1-285-22534-0. Retrieved 2022-12-02.
Axial parallelism
View on Grokipediafrom Grokipedia
Axial parallelism is the characteristic of the Earth's rotational axis by which it maintains a fixed direction in space, remaining parallel to its initial orientation as the planet orbits the Sun over the course of a year. This property ensures that the axis, tilted at an angle of approximately 23.5 degrees relative to the orbital plane (known as the obliquity of the ecliptic), does not waver or realign during revolution.[1]
The phenomenon arises from the conservation of the Earth's angular momentum, a consequence of its high rotational inertia and the absence of significant external torques from the Sun's gravitational field that could alter the spin axis direction. In essence, the rapid daily rotation (once every 24 hours) imparts gyroscopic stability, akin to the rigidity observed in spinning tops or gyroscopes, preventing the axis from shifting as the Earth travels along its elliptical path. This fixed alignment points the north end of the axis toward the star Polaris (the North Star) throughout the orbit.[2][3][4]
Axial parallelism, in combination with the constant axial tilt, is fundamental to the generation of Earth's seasons, as it causes the Northern and Southern Hemispheres to alternately face toward or away from the Sun at different points in the orbit. For instance, when the Northern Hemisphere tilts toward the Sun (around June), sunlight strikes it more directly, leading to summer with longer days and higher solar intensity; conversely, the tilt away (around December) results in winter with oblique sunlight and shorter days. This cyclic variation in insolation drives global climate patterns, including the solstices and equinoxes, and defines the Tropic of Cancer (23.5°N) and Tropic of Capricorn (23.5°S) as the latitudes experiencing the most extreme seasonal sunlight angles. The same principle applies to other rotating celestial bodies, such as other planets in the Solar System, maintaining their spin axes' orientations amid orbital motion.[1][5]