Cyclomatic complexity

There are multiple ways to define cyclomatic complexity of a section of source code. One common way is the number of linearly independent paths within it. A set ${\displaystyle S}$ of paths is linearly independent if the edge set of any path ${\displaystyle P}$ in ${\displaystyle S}$ is not the union of edge sets of the paths in some subset of ${\displaystyle S/P}$. If the source code contained no control flow statements (conditionals or decision points) the complexity would be 1, since there would be only a single path through the code. If the code had one single-condition IF statement, there would be two paths through the code: one where the IF statement is TRUE and another one where it is FALSE. Here, the complexity would be 2. Two nested single-condition IFs, or one IF with two conditions, would produce a complexity of 3.

Another way to define the cyclomatic complexity of a program is to look at its control-flow graph, a directed graph containing the basic blocks of the program, with an edge between two basic blocks if control may pass from the first to the second. The complexity M is then defined as^[2]

$${\displaystyle M=E-N+2P,}$$

where

• E = the number of edges of the graph.
• N = the number of nodes of the graph.
• P = the number of connected components.

An alternative formulation of this, as originally proposed, is to use a graph in which each exit point is connected back to the entry point. In this case, the graph is strongly connected. Here, the cyclomatic complexity of the program is equal to the cyclomatic number of its graph (also known as the first Betti number), which is defined as^[2] $${\displaystyle M=E-N+P.}$$

This may be seen as calculating the number of linearly independent cycles that exist in the graph: those cycles that do not contain other cycles within themselves. Because each exit point loops back to the entry point, there is at least one such cycle for each exit point.

For a single program (or subroutine or method), P always equals 1; a simpler formula for a single subroutine is^[3] $${\displaystyle M=E-N+2.}$$

Cyclomatic complexity may be applied to several such programs or subprograms at the same time (to all of the methods in a class, for example). In these cases, P will equal the number of programs in question, and each subprogram will appear as a disconnected subset of the graph.

McCabe showed that the cyclomatic complexity of a structured program with only one entry point and one exit point is equal to the number of decision points ("if" statements or conditional loops) contained in that program plus one. This is true only for decision points counted at the lowest, machine-level instructions.^[4] Decisions involving compound predicates like those found in high-level languages like IF cond1 AND cond2 THEN ... should be counted in terms of predicate variables involved. In this example, one should count two decision points because at machine level it is equivalent to IF cond1 THEN IF cond2 THEN ....^[2][5]

Cyclomatic complexity may be extended to a program with multiple exit points. In this case, it is equal to $${\displaystyle \pi -s+2,}$$ where ${\displaystyle \pi }$ is the number of decision points in the program and s is the number of exit points.^[5][6]

In his presentation "Software Quality Metrics to Identify Risk"^[7] for the Department of Homeland Security, Tom McCabe introduced the following categorization of cyclomatic complexity:

• 1 - 10: Simple procedure, little risk
• 11 - 20: More complex, moderate risk
• 21 - 50: Complex, high risk
• > 50: Untestable code, very high risk

An even subgraph of a graph (also known as an Eulerian subgraph) is one in which every vertex is incident with an even number of edges. Such subgraphs are unions of cycles and isolated vertices. Subgraphs will be identified with their edge sets, which is equivalent to only considering those even subgraphs which contain all vertices of the full graph.

The set of all even subgraphs of a graph is closed under symmetric difference, and may thus be viewed as a vector space over GF(2). This vector space is called the cycle space of the graph. The cyclomatic number of the graph is defined as the dimension of this space. Since GF(2) has two elements and the cycle space is necessarily finite, the cyclomatic number is also equal to the 2-logarithm of the number of elements in the cycle space.

A basis for the cycle space is easily constructed by first fixing a spanning forest of the graph, and then considering the cycles formed by one edge not in the forest and the path in the forest connecting the endpoints of that edge. These cycles form a basis for the cycle space. The cyclomatic number also equals the number of edges not in a maximal spanning forest of a graph. Since the number of edges in a maximal spanning forest of a graph is equal to the number of vertices minus the number of components, the formula ${\displaystyle E-N+P}$ defines the cyclomatic number.^[8]

Cyclomatic complexity can also be defined as a relative Betti number, the size of a relative homology group:$${\displaystyle M:=b_{1}(G,t):=\operatorname {rank} H_{1}(G,t),}$$

which is read as "the rank of the first homology group of the graph G relative to the terminal nodes t". This is a technical way of saying "the number of linearly independent paths through the flow graph from an entry to an exit", where:

• "linearly independent" corresponds to homology, and backtracking is not double-counted;
• "paths" corresponds to first homology (a path is a one-dimensional object); and
• "relative" means the path must begin and end at an entry (or exit) point.

This cyclomatic complexity can be calculated. It may also be computed via absolute Betti number by identifying the terminal nodes on a given component, or drawing paths connecting the exits to the entrance. The new, augmented graph ${\displaystyle {\tilde {G}}}$ obtains $${\displaystyle M=b_{1}({\tilde {G}})=\operatorname {rank} H_{1}({\tilde {G}}).}$$

It can also be computed via homotopy. If a (connected) control-flow graph is considered a one-dimensional CW complex called ${\displaystyle X}$, the fundamental group of ${\displaystyle X}$ will be ${\displaystyle \pi _{1}(X)\cong \mathbb {Z} ^{*n}}$. The value of ${\displaystyle n+1}$ is the cyclomatic complexity. The fundamental group counts how many loops there are through the graph up to homotopy, aligning as expected.

One of McCabe's original applications was to limit the complexity of routines during program development. He recommended that programmers should count the complexity of the modules they are developing, and split them into smaller modules whenever the cyclomatic complexity of the module exceeded 10.^[2] This practice was adopted by the NIST Structured Testing methodology, which observed that since McCabe's original publication, the figure of 10 had received substantial corroborating evidence. However, it also noted that in some circumstances it may be appropriate to relax the restriction and permit modules with a complexity as high as 15. As the methodology acknowledged that there were occasional reasons for going beyond the agreed-upon limit, it phrased its recommendation as "For each module, either limit cyclomatic complexity to [the agreed-upon limit] or provide a written explanation of why the limit was exceeded."^[9]

Section VI of McCabe's 1976 paper is concerned with determining what the control-flow graphs (CFGs) of non-structured programs look like in terms of their subgraphs, which McCabe identified. (For details, see structured program theorem.) McCabe concluded that section by proposing a numerical measure of how close to the structured programming ideal a given program is, i.e. its "structuredness". McCabe called the measure he devised for this purpose essential complexity.^[2]

To calculate this measure, the original CFG is iteratively reduced by identifying subgraphs that have a single-entry and a single-exit point, which are then replaced by a single node. This reduction corresponds to what a human would do if they extracted a subroutine from the larger piece of code. (Nowadays such a process would fall under the umbrella term of refactoring.) McCabe's reduction method was later called condensation in some textbooks, because it was seen as a generalization of the condensation to components used in graph theory.^[10] If a program is structured, then McCabe's reduction/condensation process reduces it to a single CFG node. In contrast, if the program is not structured, the iterative process will identify the irreducible part. The essential complexity measure defined by McCabe is simply the cyclomatic complexity of this irreducible graph, so it will be precisely 1 for all structured programs, but greater than one for non-structured programs.^[9]: 80

Another application of cyclomatic complexity is in determining the number of test cases that are necessary to achieve thorough test coverage of a particular module.

It is useful because of two properties of the cyclomatic complexity, M, for a specific module:

• M is an upper bound for the number of test cases that are necessary to achieve a complete branch coverage.
• M is a lower bound for the number of paths through the control-flow graph (CFG). Assuming each test case takes one path, the number of cases needed to achieve path coverage is equal to the number of paths that can actually be taken. But some paths may be impossible, so although the number of paths through the CFG is clearly an upper bound on the number of test cases needed for path coverage, this latter number (of possible paths) is sometimes less than M.

All three of the above numbers may be equal: branch coverage ${\displaystyle \leq }$ cyclomatic complexity ${\displaystyle \leq }$ number of paths.

For example, consider a program that consists of two sequential if-then-else statements.

if (c1())
    f1();
else
    f2();

if (c2())
    f3();
else
    f4();

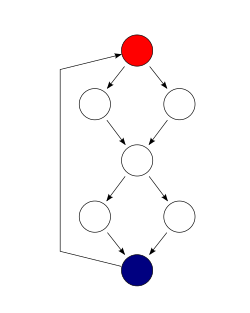
In this example, two test cases are sufficient to achieve a complete branch coverage, while four are necessary for complete path coverage. The cyclomatic complexity of the program is 3 (as the strongly connected graph for the program contains 8 edges, 7 nodes, and 1 connected component) (8 − 7 + 2).

In general, in order to fully test a module, all execution paths through the module should be exercised. This implies a module with a high complexity number requires more testing effort than a module with a lower value since the higher complexity number indicates more pathways through the code. This also implies that a module with higher complexity is more difficult to understand since the programmer must understand the different pathways and the results of those pathways.

Unfortunately, it is not always practical to test all possible paths through a program. Considering the example above, each time an additional if-then-else statement is added, the number of possible paths grows by a factor of 2. As the program grows in this fashion, it quickly reaches the point where testing all of the paths becomes impractical.

One common testing strategy, espoused for example by the NIST Structured Testing methodology, is to use the cyclomatic complexity of a module to determine the number of white-box tests that are required to obtain sufficient coverage of the module. In almost all cases, according to such a methodology, a module should have at least as many tests as its cyclomatic complexity. In most cases, this number of tests is adequate to exercise all the relevant paths of the function.^[9]

As an example of a function that requires more than mere branch coverage to test accurately, reconsider the above function. However, assume that to avoid a bug occurring, any code that calls either f1() or f3() must also call the other.^[a] Assuming that the results of c1() and c2() are independent, the function as presented above contains a bug. Branch coverage allows the method to be tested with just two tests, such as the following test cases:

• c1() returns true and c2() returns true
• c1() returns false and c2() returns false

Neither of these cases exposes the bug. If, however, we use cyclomatic complexity to indicate the number of tests we require, the number increases to 3. We must therefore test one of the following paths:

• c1() returns true and c2() returns false
• c1() returns false and c2() returns true

Either of these tests will expose the bug.

Multiple studies have investigated the correlation between McCabe's cyclomatic complexity number with the frequency of defects occurring in a function or method.^[11] Some studies^[12] find a positive correlation between cyclomatic complexity and defects; functions and methods that have the highest complexity tend to also contain the most defects. However, the correlation between cyclomatic complexity and program size (typically measured in lines of code) has been demonstrated many times. Les Hatton has claimed^[13] that complexity has the same predictive ability as lines of code. Studies that controlled for program size (i.e., comparing modules that have different complexities but similar size) are generally less conclusive, with many finding no significant correlation, while others do find correlation. Some researchers question the validity of the methods used by the studies finding no correlation.^[14] Although this relation likely exists, it is not easily used in practice.^[15] Since program size is not a controllable feature of commercial software, the usefulness of McCabe's number has been questioned.^[11] The essence of this observation is that larger programs tend to be more complex and to have more defects. Reducing the cyclomatic complexity of code is not proven to reduce the number of errors or bugs in that code. International safety standards like ISO 26262, however, mandate coding guidelines that recommend to monitor and aim to reduce code complexity, where complexity is high additional measures including scrutiny of the more difficult verification and validation activities including testing is expected.^[16]

• Programming complexity
• Complexity trap
• Computer program
• Computer programming
• Control flow
• Decision-to-decision path
• Design predicates
• Essential complexity (numerical measure of "structuredness")
• Halstead complexity measures
• Software engineering
• Software testing
• Static program analysis
• Maintainability