Leonhard Euler

Leonhard Euler was born in Basel on 15 April 1707 to Paul III Euler, a pastor of the Reformed Church, and Marguerite (née Brucker), whose ancestors include a number of well-known scholars in the classics.^[16] He was the oldest of four children, with two younger sisters, Anna Maria and Maria Magdalena, and a younger brother, Johann Heinrich.^[17][16] Soon after Leonhard's birth, the Eulers moved from Basel to Riehen, Switzerland, where his father became pastor in the local church and Leonhard spent most of his childhood.^[16]

From a young age, Euler received schooling in mathematics from his father, who had taken courses from Jacob Bernoulli some years earlier at the University of Basel. Around the age of eight, Euler was sent to live at his maternal grandmother's house and enrolled in the Latin school in Basel. In addition, he received private tutoring from Johannes Burckhardt, a young theologian with a keen interest in mathematics.^[16]

In 1720, at age 13, Euler enrolled at the University of Basel.^[4] Attending university at such a young age was not unusual at the time.^[16] The course on elementary mathematics was given by Johann Bernoulli, the younger brother of the deceased Jacob Bernoulli, who had taught Euler's father. Johann Bernoulli and Euler soon got to know each other better. Euler described Bernoulli in his autobiography:^[18]

the famous professor Johann Bernoulli [...] made it a special pleasure for himself to help me along in the mathematical sciences. Private lessons, however, he refused because of his busy schedule. However, he gave me a far more salutary advice, which consisted in myself getting a hold of some of the more difficult mathematical books and working through them with great diligence, and should I encounter some objections or difficulties, he offered me free access to him every Saturday afternoon, and he was gracious enough to comment on the collected difficulties, which was done with such a desired advantage that, when he resolved one of my objections, ten others at once disappeared, which certainly is the best method of making happy progress in the mathematical sciences.

During this time, Euler, backed by Bernoulli, obtained his father's consent to become a mathematician instead of a pastor.^[19][20]

In 1723, Euler received a Master of Philosophy with a dissertation that compared the philosophies of René Descartes and Isaac Newton.^[16] Afterwards, he enrolled in the theological faculty of the University of Basel.^[20]

In 1726, Euler completed a dissertation on the propagation of sound titled De Sono,^[21][22] with which he unsuccessfully attempted to obtain a position at the University of Basel.^[23] In 1727, he entered the Paris Academy prize competition (offered annually and later biennially by the academy beginning in 1720)^[24] for the first time. The problem posed that year was to find the best way to place the masts on a ship. Pierre Bouguer, who became known as "the father of naval architecture", won and Euler took second place.^[25] Over the years, Euler entered this competition 15 times,^[24] winning 12 of them.^[25]

Johann Bernoulli's two sons, Daniel and Nicolaus, entered into service at the Imperial Russian Academy of Sciences in Saint Petersburg in 1725, leaving Euler with the assurance they would recommend him to a post when one was available.^[23] On 31 July 1726, Nicolaus died of appendicitis after spending less than a year in Russia.^[26][27] When Daniel assumed his brother's position in the mathematics/physics division, he recommended that the post in physiology that he had vacated be filled by his friend Euler.^[23] In November 1726, Euler eagerly accepted the offer, but delayed making the trip to Saint Petersburg while he unsuccessfully applied for a physics professorship at the University of Basel.^[23]

Euler arrived in Saint Petersburg in May 1727.^[23][20] He was promoted from his junior post in the medical department of the academy to a position in the mathematics department. He lodged with Daniel Bernoulli with whom he worked in close collaboration.^[28] Euler mastered Russian, settled into life in Saint Petersburg and took on an additional job as a medic in the Russian Navy.^[29]

The academy at Saint Petersburg, established by Peter the Great, was intended to improve education in Russia and to close the scientific gap with Western Europe. As a result, it was made especially attractive to foreign scholars like Euler.^[25] The academy's benefactress, Catherine I, who had continued the progressive policies of her late husband, died before Euler's arrival to Saint Petersburg.^[30] The Russian conservative nobility then gained power upon the ascension of the twelve-year-old Peter II.^[30] The nobility, suspicious of the academy's foreign scientists, cut funding for Euler and his colleagues and prevented the entrance of foreign and non-aristocratic students into the Gymnasium and universities.^[30]

Conditions improved slightly after the death of Peter II in 1730 and the German-influenced Anna of Russia assumed power.^[31] Euler swiftly rose through the ranks in the academy and was made a professor of physics in 1731.^[31] He also left the Russian Navy, refusing a promotion to lieutenant.^[31] Two years later, Daniel Bernoulli, fed up with the censorship and hostility he faced at Saint Petersburg, left for Basel. Euler succeeded him as the head of the mathematics department.^[32] In January 1734, he married Katharina Gsell (1707–1773), a daughter of Georg Gsell.^[33] Frederick II had made an attempt to recruit the services of Euler for his newly established Berlin Academy in 1740, but Euler initially preferred to stay in St Petersburg.^[34] But after Empress Anna died and Frederick II agreed to pay 1600 ecus (the same as Euler earned in Russia) he agreed to move to Berlin. In 1741, he requested permission to leave for Berlin, arguing he was in need of a milder climate for his eyesight.^[34] The Russian academy gave its consent and would pay him 200 rubles per year as one of its active members.^[34]

Concerned about the continuing turmoil in Russia, Euler left St. Petersburg in June 1741 to take up a post at the Berlin Academy, which he had been offered by Frederick the Great of Prussia.^[35] He lived for 25 years in Berlin, where he wrote several hundred articles.^[20] In 1748 his text on functions called the Introductio in analysin infinitorum was published and in 1755 a text on differential calculus called the Institutiones calculi differentialis was published.^[36][37] In 1755, he was elected a foreign member of the Royal Swedish Academy of Sciences^[38] and of the French Academy of Sciences.^[39] Notable students of Euler in Berlin included Stepan Rumovsky, later considered as the first Russian astronomer.^[40][41] In 1748 he declined an offer from the University of Basel to succeed the recently deceased Johann Bernoulli.^[20] In 1753 he bought a house in Charlottenburg, in which he lived with his family and widowed mother.^[42][43]

Euler became the tutor for Friederike Charlotte of Brandenburg-Schwedt, the Princess of Anhalt-Dessau and Frederick's niece. He wrote over 200 letters to her in the early 1760s, which were later compiled into a volume entitled Letters of Euler on different Subjects in Natural Philosophy Addressed to a German Princess.^[44] This work contained Euler's exposition on various subjects pertaining to physics and mathematics and offered valuable insights into Euler's personality and religious beliefs. It was translated into multiple languages, published across Europe and in the United States, and became more widely read than any of his mathematical works. The popularity of the Letters testifies to Euler's ability to communicate scientific matters effectively to a lay audience, a rare ability for a dedicated research scientist.^[37]

Despite Euler's immense contribution to the academy's prestige and having been put forward as a candidate for its presidency by Jean le Rond d'Alembert, Frederick II named himself as its president.^[43] The Prussian king had a large circle of intellectuals in his court, and he found the mathematician unsophisticated and ill-informed on matters beyond numbers and figures. Euler was a simple, devoutly religious man who never questioned the existing social order or conventional beliefs. He was, in many ways, the polar opposite of Voltaire, who enjoyed a high place of prestige at Frederick's court. Euler was not a skilled debater and often made it a point to argue subjects that he knew little about, making him the frequent target of Voltaire's wit.^[37] Frederick also expressed disappointment with Euler's practical engineering abilities, stating:

I wanted to have a water jet in my garden: Euler calculated the force of the wheels necessary to raise the water to a reservoir, from where it should fall back through channels, finally spurting out in Sanssouci. My mill was carried out geometrically and could not raise a mouthful of water closer than fifty paces to the reservoir. Vanity of vanities! Vanity of geometry!^[45]

However, the disappointment was almost surely unwarranted from a technical perspective. Euler's calculations look likely to be correct, even if Euler's interactions with Frederick and those constructing his fountain may have been dysfunctional.^[46]

Throughout his stay in Berlin, Euler maintained a strong connection to the academy in St. Petersburg and also published 109 papers in Russia.^[47] He also assisted students from the St. Petersburg academy and at times accommodated Russian students in his house in Berlin.^[47] In 1760, with the Seven Years' War raging, Euler's farm in Charlottenburg was sacked by advancing Russian troops.^[42] Upon learning of this event, General Ivan Petrovich Saltykov paid compensation for the damage caused to Euler's estate, with Empress Elizabeth of Russia later adding a further payment of 4000 rubles—an exorbitant amount at the time.^[48] Euler decided to leave Berlin in 1766 and return to Russia.^[49]

During his Berlin years (1741–1766), Euler was at the peak of his productivity. He wrote 380 works, 275 of which were published.^[50] This included 125 memoirs in the Berlin Academy and over 100 memoirs sent to the St. Petersburg Academy, which had retained him as a member and paid him an annual stipend. Euler's Introductio in Analysin Infinitorum was published in two parts in 1748. In addition to his own research, Euler supervised the library, the observatory, the botanical garden, and the publication of calendars and maps from which the academy derived income.^[51] He was even involved in the design of the water fountains at Sanssouci, the King's summer palace.^[52]

The political situation in Russia stabilized after Catherine the Great's accession to the throne, so in 1766 Euler accepted an invitation to return to the St. Petersburg Academy. His conditions were quite exorbitant—a 3000 ruble annual salary, a pension for his wife, and the promise of high-ranking appointments for his sons. At the university he was assisted by his student Anders Johan Lexell.^[53] While living in St. Petersburg, a fire in 1771 destroyed his home.^[54]

On 7 January 1734, Euler married Katharina Gsell, daughter of Georg Gsell, a painter at the Academy Gymnasium in Saint Petersburg.^[33] The couple bought a house by the Neva River.

Of their 13 children, five survived childhood,^[55] three sons and two daughters.^[56] Their first son was Johann Albrecht Euler, whose godfather was Christian Goldbach.^[56]

Three years after his wife's death in 1773,^[54] Euler married her half-sister, Salome Abigail Gsell.^[57] This marriage lasted until his death in 1783.

His brother Johann Heinrich settled in St. Petersburg in 1735 and was employed as a painter at the academy.^[34]

Early in his life, Euler memorized Virgil's Aeneid, and by old age, he could recite the poem and give the first and last sentence on each page of the edition from which he had learnt it.^[58][59] Euler knew the first hundred prime numbers and could give each of their powers up to the sixth degree.^[60]

Euler was known as a generous and kind person, not neurotic as seen in some geniuses, keeping his good-natured disposition even after becoming entirely blind.^[60]

Euler's eyesight worsened throughout his mathematical career. In 1738, three years after nearly dying of fever,^[61] he became almost blind in his right eye. Euler blamed the cartography he performed for the St. Petersburg Academy for his condition,^[62] but the cause of his blindness remains the subject of speculation.^[63][64] Euler's vision in that eye worsened throughout his stay in Germany, to the extent that Frederick called him "Cyclops". Euler said of his loss of vision, "Now I will have fewer distractions."^[62] In 1766 a cataract in his left eye was discovered. Though couching of the cataract temporarily improved his vision, complications rendered him almost totally blind in the left eye as well.^[39] His condition appeared to have little effect on his productivity. With the aid of his scribes, Euler's productivity in many areas of study increased;^[65] in 1775, he produced, on average, one mathematical paper per week.^[39]

In St. Petersburg on 18 September 1783, after a lunch with his family, Euler was discussing the newly discovered planet Uranus and its orbit with Anders Johan Lexell when he collapsed and died of a brain hemorrhage.^[63] Jacob von Staehlin [de] wrote a short obituary for the Russian Academy of Sciences and Russian mathematician Nicolas Fuss, one of Euler's disciples, wrote a more detailed eulogy,^[55] which he delivered at a memorial meeting. In his eulogy for the French Academy, French mathematician and philosopher Marquis de Condorcet wrote:

... il cessa de calculer et de vivre.

... he ceased to calculate and to live.^[66]

Euler was buried next to Katharina at the Smolensk Lutheran Cemetery on Vasilievsky Island. In 1837, the Russian Academy of Sciences installed a new monument, replacing his overgrown grave plaque. In 1957, to commemorate the 250th anniversary of his birth, his tomb was moved to the Lazarevskoe Cemetery at the Alexander Nevsky Monastery.^[67]

Part of a series of articles on the
mathematical constant e
Properties
Natural logarithm Exponential function
Applications
compound interest Euler's identity Euler's formula half-lives exponential growth and decay
Defining e
proof that e is irrational representations of e Lindemann–Weierstrass theorem
People
John Napier Leonhard Euler
Related topics
Schanuel's conjecture
v t e

Euler worked in almost all areas of mathematics, including geometry, infinitesimal calculus, trigonometry, algebra, and number theory, as well as continuum physics, lunar theory, and other areas of physics. He is a seminal figure in the history of mathematics; if printed, his works, many of which are of fundamental interest, would occupy between 60 and 80 quarto volumes.^[39] Euler's name is associated with a large number of topics. Euler's work averages 800 pages a year from 1725 to 1783. He also wrote over 4500 letters and hundreds of manuscripts. It has been estimated that Leonhard Euler was the author of a quarter of the combined output in mathematics, physics, mechanics, astronomy, and navigation in the 18th century, while other researchers credit Euler for a third of the output in mathematics in that century.^[6]

Euler introduced and popularized several notational conventions through his numerous and widely circulated textbooks. Most notably, he introduced the concept of a function^[3] and was the first to write f(x) to denote the function f applied to the argument x. He also introduced the modern notation for the trigonometric functions, the letter e for the base of the natural logarithm (now also known as Euler's number), the Greek letter Σ for summations and the letter i to denote the imaginary unit.^[68] The use of the Greek letter π to denote the ratio of a circle's circumference to its diameter was also popularized by Euler, although it originated with Welsh mathematician William Jones.^[69]

The development of infinitesimal calculus was at the forefront of 18th-century mathematical research, and the Bernoullis—family friends of Euler—were responsible for much of the early progress in the field. Thanks to their influence, studying calculus became the major focus of Euler's work. While some of Euler's proofs are not acceptable by modern standards of mathematical rigour^[70] (in particular his reliance on the principle of the generality of algebra), his ideas led to many great advances. Euler is well known in analysis for his frequent use and development of power series, the expression of functions as sums of infinitely many terms,^[71] such as $${\displaystyle e^{x}=\sum _{n=0}^{\infty }{x^{n} \over n!}=\lim _{n\to \infty }\left({\frac {1}{0!}}+{\frac {x}{1!}}+{\frac {x^{2}}{2!}}+\cdots +{\frac {x^{n}}{n!}}\right).}$$

Euler's use of power series enabled him to solve the Basel problem, finding the sum of the reciprocals of squares of every natural number, in 1735 (he provided a more elaborate argument in 1741). The Basel problem was originally posed by Pietro Mengoli in 1644, and by the 1730s was a famous open problem, popularized by Jacob Bernoulli and unsuccessfully attacked by many of the leading mathematicians of the time. Euler found that:^[72][73][70]

$${\displaystyle \sum _{n=1}^{\infty }{1 \over n^{2}}=\lim _{n\to \infty }\left({\frac {1}{1^{2}}}+{\frac {1}{2^{2}}}+{\frac {1}{3^{2}}}+\cdots +{\frac {1}{n^{2}}}\right)={\frac {\pi ^{2}}{6}}.}$$

Euler introduced the constant $${\displaystyle \gamma =\lim _{n\rightarrow \infty }\left(1+{\frac {1}{2}}+{\frac {1}{3}}+{\frac {1}{4}}+\cdots +{\frac {1}{n}}-\ln(n)\right)\approx 0.5772,}$$ now known as Euler's constant or the Euler–Mascheroni constant, and studied its relationship with the harmonic series, the gamma function, and values of the Riemann zeta function.^[74]

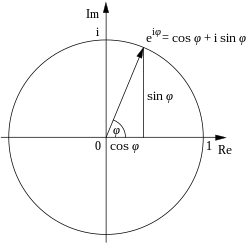
Euler introduced the use of the exponential function and logarithms in analytic proofs. He discovered ways to express various logarithmic functions using power series, and he successfully defined logarithms for negative and complex numbers, thus greatly expanding the scope of mathematical applications of logarithms.^[68] He also defined the exponential function for complex numbers and discovered its relation to the trigonometric functions. For any real number φ (taken to be radians), Euler's formula states that the complex exponential function satisfies $${\displaystyle e^{i\varphi }=\cos \varphi +i\sin \varphi }$$

which was called "the most remarkable formula in mathematics" by Richard Feynman.^[75]

A special case of the above formula is known as Euler's identity, $${\displaystyle e^{i\pi }+1=0}$$

Euler elaborated the theory of higher transcendental functions by introducing the gamma function^[76][77] and introduced a new method for solving quartic equations.^[78] He found a way to calculate integrals with complex limits, foreshadowing the development of modern complex analysis. He invented the calculus of variations and formulated the Euler–Lagrange equation for reducing optimization problems in this area to the solution of differential equations.

Euler pioneered the use of analytic methods to solve number theory problems. In doing so, he united two disparate branches of mathematics and introduced a new field of study, analytic number theory. In breaking ground for this new field, Euler created the theory of hypergeometric series, q-series, hyperbolic trigonometric functions, and the analytic theory of continued fractions. For example, he proved the infinitude of primes using the divergence of the harmonic series, and he used analytic methods to gain some understanding of the way prime numbers are distributed. Euler's work in this area led to the development of the prime number theorem.^[79]

Euler's interest in number theory can be traced to the influence of Christian Goldbach,^[80] his friend in the St. Petersburg Academy.^[61] Much of Euler's early work on number theory was based on the work of Pierre de Fermat. Euler developed some of Fermat's ideas and disproved some of his conjectures, such as his conjecture that all numbers of the form ${\textstyle 2^{2^{n}}+1}$ (Fermat numbers) are prime.^[81]

Euler linked the nature of prime distribution with ideas in analysis. He proved that the sum of the reciprocals of the primes diverges. In doing so, he discovered the connection between the Riemann zeta function and prime numbers; this is known as the Euler product formula for the Riemann zeta function.^[82]

Euler invented the totient function φ(n), the number of positive integers less than or equal to the integer n that are coprime to n. Using properties of this function, he generalized Fermat's little theorem to what is now known as Euler's theorem.^[83] He contributed significantly to the theory of perfect numbers, which had fascinated mathematicians since Euclid. He proved that the relationship shown between even perfect numbers and Mersenne primes (which he had earlier proved) was one-to-one, a result otherwise known as the Euclid–Euler theorem.^[84] Euler also conjectured the law of quadratic reciprocity. The concept is regarded as a fundamental theorem within number theory, and his ideas paved the way for the work of Carl Friedrich Gauss, particularly Disquisitiones Arithmeticae.^[85] By 1772 Euler had proved that 2³¹ − 1 = 2,147,483,647 is a Mersenne prime. It may have remained the largest known prime until 1867.^[86]

Euler also contributed major developments to the theory of partitions of an integer.^[87]

In 1735, Euler presented a solution to the problem known as the Seven Bridges of Königsberg.^[88] The city of Königsberg, Prussia was set on the Pregel River, and included two large islands that were connected to each other and the mainland by seven bridges. The problem is to decide whether it is possible to follow a path that crosses each bridge exactly once. Euler showed that it is not possible: there is no Eulerian path. This solution is considered to be the first theorem of graph theory.^[88]

Euler also discovered the formula ${\displaystyle V-E+F=2}$ relating the number of vertices, edges, and faces of a convex polyhedron,^[89] and hence of a planar graph. The constant in this formula is now known as the Euler characteristic for the graph (or other mathematical object), and is related to the genus of the object.^[90] The study and generalization of this formula, specifically by Cauchy^[91] and L'Huilier,^[92] is at the origin of topology.^[89]

Part of a series on
Classical mechanics
${\displaystyle {\textbf {F}}={\frac {d\mathbf {p} }{dt}}}$ Second law of motion
History Timeline Textbooks
Branches Applied Celestial Continuum Dynamics Field theory Kinematics Kinetics Statics Statistical mechanics
Fundamentals Acceleration Angular momentum Couple D'Alembert's principle Energy kinetic potential Force Frame of reference Inertial frame of reference Impulse Inertia / Moment of inertia Mass Mechanical power Mechanical work Moment Momentum Space Speed Time Torque Velocity Virtual work
Formulations Newton's laws of motion Analytical mechanics Lagrangian mechanics Hamiltonian mechanics Routhian mechanics Hamilton–Jacobi equation Appell's equation of motion Koopman–von Neumann mechanics
Core topics Damping Displacement Equations of motion Euler's laws of motion Fictitious force Friction Harmonic oscillator Inertial / Non-inertial reference frame Motion (linear) Newton's law of universal gravitation Newton's laws of motion Relative velocity Rigid body dynamics Euler's equations Simple harmonic motion Vibration
Rotation Circular motion Rotating reference frame Centripetal force Centrifugal force reactive Coriolis force Pendulum Tangential speed Rotational frequency Angular acceleration / displacement / frequency / velocity
Scientists Kepler Galileo Huygens Newton Horrocks Halley Maupertuis Daniel Bernoulli Johann Bernoulli Euler d'Alembert Clairaut Lagrange Laplace Poisson Hamilton Jacobi Cauchy Routh Liouville Appell Gibbs Koopman von Neumann
Physics portal  Category
v t e

Some of Euler's greatest successes were in solving real-world problems analytically, and in describing numerous applications of the Bernoulli numbers, Fourier series, Euler numbers, the constants e and π, continued fractions, and integrals. He integrated Leibniz's differential calculus with Newton's Method of Fluxions, and developed tools that made it easier to apply calculus to physical problems. He made great strides in improving the numerical approximation of integrals, inventing what are now known as the Euler approximations. The most notable of these approximations are Euler's method^[93] and the Euler–Maclaurin formula.^[94][95][96]

Euler helped develop the Euler–Bernoulli beam equation, which became a cornerstone of engineering.^[97] Besides successfully applying his analytic tools to problems in classical mechanics, Euler applied these techniques to celestial problems. His work in astronomy was recognized by multiple Paris Academy Prizes over the course of his career. His accomplishments include determining with great accuracy the orbits of comets and other celestial bodies, understanding the nature of comets, and calculating the parallax of the Sun. His calculations contributed to the development of accurate longitude tables.^[98]

Euler made important contributions in optics.^[99] He disagreed with Newton's corpuscular theory of light,^[100] which was the prevailing theory of the time. His 1740s papers on optics helped ensure that the wave theory of light proposed by Christiaan Huygens would become the dominant mode of thought, at least until the development of the quantum theory of light.^[101]

In fluid dynamics, Euler was the first to predict the phenomenon of cavitation, in 1754, long before its first observation in the late 19th century, and the Euler number used in fluid flow calculations comes from his related work on the efficiency of turbines.^[102] In 1757 he published an important set of equations for inviscid flow in fluid dynamics, that are now known as the Euler equations.^[103]

Euler is well known in structural engineering for his formula giving Euler's critical load, the critical buckling load of an ideal strut, which depends only on its length and flexural stiffness.^[104]

Euler is credited with using closed curves to illustrate syllogistic reasoning (1768). These diagrams have become known as Euler diagrams.^[105]

An Euler diagram is a diagrammatic means of representing sets and their relationships. Euler diagrams consist of simple closed curves (usually circles) in the plane that depict sets. Each Euler curve divides the plane into two regions or "zones": the interior, which symbolically represents the elements of the set, and the exterior, which represents all elements that are not members of the set. The sizes or shapes of the curves are not important; the significance of the diagram is in how they overlap. The spatial relationships between the regions bounded by each curve (overlap, containment or neither) corresponds to set-theoretic relationships (intersection, subset, and disjointness). Curves whose interior zones do not intersect represent disjoint sets. Two curves whose interior zones intersect represent sets that have common elements; the zone inside both curves represents the set of elements common to both sets (the intersection of the sets). A curve that is contained completely within the interior zone of another represents a subset of it.

Euler diagrams (and their refinement to Venn diagrams) were incorporated as part of instruction in set theory as part of the new math movement in the 1960s.^[106] Since then, they have come into wide use as a way of visualizing combinations of characteristics.^[107]

In his 1760 paper A General Investigation into the Mortality and Multiplication of the Human Species Euler produced a model which showed how a population with constant fertility and mortality might grow geometrically using a difference equation. Under this geometric growth Euler also examined relationships among various demographic indices showing how they might be used to produce estimates when observations were missing. Three papers published around 150 years later by Alfred J. Lotka (1907, 1911 (with F.R. Sharpe) and 1922) adopted a similar approach to Euler's and produced their Stable Population Model. These marked the start of 20th century formal demographic modelling.^{[108][109][110][111][112][113]}

One of Euler's more unusual interests was the application of mathematical ideas in music. In 1739 he wrote the Tentamen novae theoriae musicae (Attempt at a New Theory of Music), hoping to eventually incorporate musical theory as part of mathematics. This part of his work, however, did not receive wide attention and was once described as too mathematical for musicians and too musical for mathematicians.^[114] Even when dealing with music, Euler's approach is mainly mathematical,^[115] for instance, his introduction of binary logarithms as a way of numerically describing the subdivision of octaves into fractional parts.^[116] His writings on music are not particularly numerous (a few hundred pages, in his total production of about thirty thousand pages), but they reflect an early preoccupation and one that remained with him throughout his life.^[115]

A first point of Euler's musical theory is the definition of "genres", i.e. of possible divisions of the octave using the prime numbers 3 and 5. Euler describes 18 such genres, with the general definition 2^mA, where A is the "exponent" of the genre (i.e. the sum of the exponents of 3 and 5) and 2^m (where "m is an indefinite number, small or large, so long as the sounds are perceptible"^[117]), expresses that the relation holds independently of the number of octaves concerned. The first genre, with A = 1, is the octave itself (or its duplicates); the second genre, 2^m.3, is the octave divided by the fifth (fifth + fourth, C–G–C); the third genre is 2^m.5, major third + minor sixth (C–E–C); the fourth is 2^m.3², two-fourths and a tone (C–F–B♭–C); the fifth is 2^m.3.5 (C–E–G–B–C); etc. Genres 12 (2^m.3³.5), 13 (2^m.3².5²) and 14 (2^m.3.5³) are corrected versions of the diatonic, chromatic and enharmonic, respectively, of the Ancients. Genre 18 (2^m.3³.5²) is the "diatonico-chromatic", "used generally in all compositions",^[118] and which turns out to be identical with the system described by Johann Mattheson.^[119] Euler later envisaged the possibility of describing genres including the prime number 7.^[120]

Euler devised a specific graph, the Speculum musicum,^[121][122] to illustrate the diatonico-chromatic genre, and discussed paths in this graph for specific intervals, recalling his interest in the Seven Bridges of Königsberg (see above). The device drew renewed interest as the Tonnetz in Neo-Riemannian theory (see also Lattice (music)).^[123]

Euler further used the principle of the "exponent" to propose a derivation of the gradus suavitatis (degree of suavity, of agreeableness) of intervals and chords from their prime factors – one must keep in mind that he considered just intonation, i.e. 1 and only the prime numbers 3 and 5.^[124] Formulas have been proposed extending this system to any number of prime numbers, e.g. in the form $${\displaystyle \ ds=\sum _{i}\left(k_{i}\cdot p_{i}-k_{i}\right)+1\ ,}$$ where p_i are prime numbers and k_i their exponents.^[125]

Euler was religious throughout his life.^[20] Much of what is known of his religious beliefs can be deduced from his Letters to a German Princess and an earlier work, Rettung der Göttlichen Offenbahrung gegen die Einwürfe der Freygeister (Defense of the Divine Revelation against the Objections of the Freethinkers). These show that Euler was a devout Christian who believed the Bible to be inspired; the Rettung was primarily an argument for the divine inspiration of scripture.^[126][127]

Euler opposed the concepts of Leibniz's monadism and the philosophy of Christian Wolff.^[128] He insisted that knowledge is founded in part on the basis of precise quantitative laws, something that monadism and Wolffian science were unable to provide. Euler called Wolff's ideas "heathen and atheistic".^[129]

There is a legend^[130] inspired by Euler's arguments with secular philosophers over religion, which is set during Euler's second stint at the St. Petersburg Academy. The French philosopher Denis Diderot was visiting Russia on Catherine the Great's invitation. The Empress was alarmed that Diderot's arguments for atheism were influencing members of her court, and so Euler was asked to confront him. Diderot was informed that a learned mathematician had produced a proof of the existence of God: he agreed to view the proof as it was presented in court. Euler appeared, advanced toward Diderot, and in a tone of perfect conviction announced this non sequitur:

"Sir, ${\displaystyle {\frac {a+b^{n}}{n}}=x}$, hence God exists –reply!"

Diderot, to whom (says the story) all mathematics was gibberish, stood dumbstruck as peals of laughter erupted from the court. Embarrassed, he asked to leave Russia, a request Catherine granted. However amusing the anecdote may be, it is apocryphal, given that Diderot himself did research in mathematics.^[131] The legend was apparently first told by Dieudonné Thiébault with embellishment by Augustus De Morgan.^[130]

Euler is widely recognized as one of the greatest mathematicians of all time, and more likely than not the most prolific contributor to mathematics and science.^[8] Mathematician and physicist John von Neumann called Euler "the greatest virtuoso of the period".^[132] Mathematician François Arago said, "Euler calculated without any apparent effort, just as men breathe and as eagles sustain themselves in air".^[133] He is generally ranked right below Carl Friedrich Gauss, Isaac Newton, and Archimedes among the greatest mathematicians of all time,^[133] while some rank him as equal with them.^[134] Physicist and mathematician Henri Poincaré called Euler the "god of mathematics".^[135]

French mathematician André Weil noted that Euler stood above his contemporaries and more than anyone else was able to cement himself as the leading force of his era's mathematics:^[132]

No mathematician ever attained such a position of undisputed leadership in all branches of mathematics, pure and applied, as Euler did for the best part of the eighteenth century.

Swiss mathematician Nicolas Fuss noted Euler's extraordinary memory and breadth of knowledge, saying:^[5]

Knowledge that we call erudition was not inimical to him. He had read all the best Roman writers, knew perfectly the ancient history of mathematics, held in his memory the historical events of all times and peoples, and could without hesitation adduce by way of examples the most trifling of historical events. He knew more about medicine, botany, and chemistry than might be expected of someone who had not worked especially in those sciences.

Euler was featured on both the sixth^[136] and seventh^[137] series of the Swiss 10-franc banknote and on numerous Swiss, German, and Russian postage stamps. In 1782 he was elected a Foreign Honorary Member of the American Academy of Arts and Sciences.^[138] The asteroid 2002 Euler was named in his honour.^[139]