Finite potential well

For the one-dimensional case on the x-axis, the time-independent Schrödinger equation can be written as:

$${\displaystyle -{\frac {\hbar ^{2}}{2m}}{\frac {d^{2}\psi }{dx^{2}}}+V(x)\psi =E\psi }$$

1

where^[1]

• ${\displaystyle \hbar }$ is the reduced Planck constant,
• ${\displaystyle m}$ is the mass of the particle,
• ${\displaystyle V(x)}$ is the potential energy at each point x,
• ${\displaystyle \psi }$ is the (complex valued) wavefunction, or "eigenfunction", and
• ${\displaystyle E}$ is the energy, a real number, sometimes called eigenenergy.

For the case of the particle in a one-dimensional box of length L, the potential is ${\displaystyle V_{0}}$ outside the box, and zero for x between ${\displaystyle -L/2}$ and ${\displaystyle L/2}$. The wavefunction is composed of different wavefunctions; depending on whether x is inside or outside of the box, such that:^[2] $${\displaystyle \psi ={\begin{cases}\psi _{1},&{\text{if }}x<-L/2{\text{ (the region outside the well)}}\\\psi _{2},&{\text{if }}-L/2<x<L/2{\text{ (the region inside the well)}}\\\psi _{3},&{\text{if }}x>L/2{\text{ (the region outside the well)}}\end{cases}}}$$

For the region inside the box, V(x) = 0 and Equation 1 reduces to^[3] $${\displaystyle -{\frac {\hbar ^{2}}{2m}}{\frac {d^{2}\psi _{2}}{dx^{2}}}=E\psi _{2},}$$ resembling the time-independent free schrödinger equation, hence $${\displaystyle E={\frac {k^{2}\hbar ^{2}}{2m}}.}$$ Letting $${\displaystyle k={\frac {\sqrt {2mE}}{\hbar }},}$$ the equation becomes $${\displaystyle {\frac {d^{2}\psi _{2}}{dx^{2}}}=-k^{2}\psi _{2}.}$$ with a general solution of $${\displaystyle \psi _{2}=A\sin(kx)+B\cos(kx)\,.}$$ where A and B can be any complex numbers, and k can be any real number.

For the region outside of the box, since the potential is constant, ${\displaystyle V(x)=V_{0}}$ and equation 1 becomes: $${\displaystyle -{\frac {\hbar ^{2}}{2m}}{\frac {d^{2}\psi _{1}}{dx^{2}}}=(E-V_{0})\psi _{1}}$$

There are two possible families of solutions, depending on whether E is less than ${\displaystyle V_{0}}$ (the particle is in a bound state) or E is greater than ${\displaystyle V_{0}}$ (the particle is in an unbounded state).

If we solve the time-independent Schrödinger equation for an energy ${\displaystyle E>V_{0}}$, letting $${\displaystyle k'={\frac {\sqrt {2m(E-V_{0})}}{\hbar }}}$$ such that $${\displaystyle {\frac {d^{2}\psi _{1}}{dx^{2}}}=-k'^{2}\psi _{1}}$$ then the solution has the same form as the inside-well case: $${\displaystyle \psi _{1}=C\sin(k'x)+D\cos(k'x)}$$ and, hence, will be oscillatory both inside and outside the well. Thus, the solution is never square integrable; that is, it is always a non-normalizable state. This does not mean, however, that it is impossible for a quantum particle to have energy greater than ${\displaystyle V_{0}}$, it merely means that the system has continuous spectrum above ${\displaystyle V_{0}}$, i.e., the non-normalizable states still contribute to the continuous part of the spectrum as generalized eigenfunctions of an unbounded operator.^[4]

This analysis will focus on the bound state, where ${\displaystyle E<V_{0}}$. Letting $${\displaystyle \alpha ={\frac {\sqrt {2m(V_{0}-E)}}{\hbar }}}$$ produces $${\displaystyle {\frac {d^{2}\psi _{1}}{dx^{2}}}=\alpha ^{2}\psi _{1}}$$ where the general solution is a real exponential: $${\displaystyle \psi _{1}=Fe^{-\alpha x}+Ge^{\alpha x}}$$

Similarly, for the other region outside the box: $${\displaystyle \psi _{3}=He^{-\alpha x}+Ie^{\alpha x}}$$

Now in order to find the specific solution for the problem at hand, we must specify the appropriate boundary conditions and find the values for A, B, F, G, H and I that satisfy those conditions.

Solutions to the Schrödinger equation must be continuous, and continuously differentiable.^[5] These requirements are boundary conditions on the differential equations previously derived, that is, the matching conditions between the solutions inside and outside the well.

In this case, the finite potential well is symmetrical, so symmetry can be exploited to reduce the necessary calculations.

Summarizing the previous sections: $${\displaystyle \psi ={\begin{cases}\psi _{1},&{\text{if }}x<-L/2{\text{ (the region outside the box)}}\\\psi _{2},&{\text{if }}-L/2<x<L/2{\text{ (the region inside the box)}}\\\psi _{3}&{\text{if }}x>L/2{\text{ (the region outside the box)}}\end{cases}}}$$ where we found ${\displaystyle \psi _{1}}$, ${\displaystyle \psi _{2}}$, and ${\displaystyle \psi _{3}}$ to be: $${\displaystyle {\begin{aligned}\psi _{1}&=Fe^{-\alpha x}+Ge^{\alpha x}\\\psi _{2}&=A\sin(kx)+B\cos(kx)\\\psi _{3}&=He^{-\alpha x}+Ie^{\alpha x}\end{aligned}}}$$

We see that as ${\displaystyle x}$ goes to ${\displaystyle -\infty }$, the ${\displaystyle F}$ term goes to infinity. Likewise, as ${\displaystyle x}$ goes to ${\displaystyle +\infty }$, the ${\displaystyle I}$ term goes to infinity. In order for the wave function to be square integrable, we must set ${\displaystyle F=I=0}$, and we have: $${\displaystyle \psi _{1}=Ge^{\alpha x}}$$ and $${\displaystyle \psi _{3}=He^{-\alpha x}}$$

Next, we know that the overall ${\displaystyle \psi }$ function must be continuous and differentiable. In other words, the values of the functions and their derivatives must match up at the dividing points:

${\displaystyle \psi _{1}(-L/2)=\psi _{2}(-L/2)}$		${\displaystyle \psi _{2}(L/2)=\psi _{3}(L/2)}$
${\displaystyle \left.{\frac {d\psi _{1}}{dx}}\right|_{x=-L/2}=\left.{\frac {d\psi _{2}}{dx}}\right|_{x=-L/2}}$		${\displaystyle \left.{\frac {d\psi _{2}}{dx}}\right|_{x=L/2}=\left.{\frac {d\psi _{3}}{dx}}\right|_{x=L/2}}$

These equations have two sorts of solutions, symmetric, for which ${\displaystyle A=0}$ and ${\displaystyle G=H}$, and antisymmetric, for which ${\displaystyle B=0}$ and ${\displaystyle G=-H}$. For the symmetric case we get $${\displaystyle He^{-\alpha L/2}=B\cos(kL/2)}$$ $${\displaystyle -\alpha He^{-\alpha L/2}=-kB\sin(kL/2)}$$ so taking the ratio gives

$${\displaystyle \alpha =k\tan(kL/2).}$$ Similarly for the antisymmetric case we get $${\displaystyle \alpha =-k\cot(kL/2).}$$

Recall that both ${\displaystyle \alpha }$ and ${\displaystyle k}$ depend on the energy. What we have found is that the continuity conditions cannot be satisfied for an arbitrary value of the energy; because that is a result of the infinite potential well case. Thus, only certain energy values, which are solutions to one or either of these two equations, are allowed. Hence we find that the energy levels of the system below ${\displaystyle V_{0}}$ are discrete; the corresponding eigenfunctions are bound states. (By contrast, for the energy levels above ${\displaystyle V_{0}}$ are continuous.^[6])

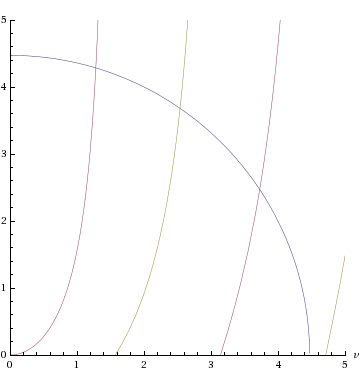
The energy equations cannot be solved analytically. Nevertheless, we will see that in the symmetric case, there always exists at least one bound state, even if the well is very shallow.^[7] Graphical or numerical solutions to the energy equations are aided by rewriting them a little and it should be mentioned that a nice approximation method has been found by Lima which works for any pair of parameters ${\displaystyle L}$ and ${\displaystyle V_{0}}$.^[8] If we introduce the dimensionless variables ${\displaystyle u=\alpha L/2}$ and ${\displaystyle v=kL/2}$, and note from the definitions of ${\displaystyle \alpha }$ and ${\displaystyle k}$ that ${\displaystyle u^{2}=u_{0}^{2}-v^{2}}$, where ${\textstyle u_{0}^{2}={\frac {1}{2}}mL^{2}V_{0}\hbar ^{-2}}$, the master equations read $${\displaystyle {\sqrt {u_{0}^{2}-v^{2}}}={\begin{cases}v\tan v,&{\text{(symmetric case) }}\\-v\cot v,&{\text{(antisymmetric case) }}\end{cases}}}$$

In the plot to the right, for ${\displaystyle u_{0}^{2}=20}$, solutions exist where the blue semicircle intersects the purple or grey curves (${\displaystyle v\tan v}$ and ${\displaystyle -v\cot v}$). Each purple or grey curve represents a possible solution, ${\displaystyle v_{j}}$ within the range ${\textstyle {\frac {\pi }{2}}(j-1)\leq v_{i}<{\frac {\pi }{2}}j}$. The total number of solutions, ${\displaystyle N}$, (i.e., the number of purple/grey curves that are intersected by the blue circle) is therefore determined by dividing the radius of the blue circle, ${\displaystyle u_{0}}$, by the range of each solution ${\displaystyle \pi /2}$ and using the floor or ceiling functions:^[9] $${\displaystyle N=\left\lfloor {\frac {2u_{0}}{\pi }}\right\rfloor +1=\left\lceil {\frac {2u_{0}}{\pi }}\right\rceil }$$

In this case there are exactly three solutions, since ${\displaystyle N=\lceil 2{\sqrt {20}}/\pi \rceil =\lceil 2.85\rceil =3}$.

${\displaystyle v_{1}=1.28,v_{2}=2.54}$ and ${\displaystyle v_{3}=3.73}$, with the corresponding energies $${\displaystyle E_{n}={2\hbar ^{2}v_{n}^{2} \over mL^{2}}.}$$ If we want, we can go back and find the values of the constants ${\displaystyle A,B,G,H}$ in the equations now (we also need to impose the normalisation condition). On the right we show the energy levels and wave functions in this case (where ${\textstyle x_{0}\equiv \hbar /{\sqrt {2mV_{0}}}}$).

We note that however small ${\displaystyle u_{0}}$ is (however shallow or narrow the well), there is always at least one bound state.

Two special cases are worth noting. As the height of the potential becomes large, ${\displaystyle V_{0}\to \infty }$, the radius of the semicircle gets larger and the roots get closer and closer to the values ${\displaystyle v_{n}=n\pi /2}$, and we recover the case of the infinite square well.

The other case is that of a very narrow, deep well - specifically the case ${\displaystyle V_{0}\to \infty }$ and ${\displaystyle L\to 0}$ with ${\displaystyle V_{0}L}$ fixed. As ${\displaystyle u_{0}\propto {\sqrt {V_{0}}}L}$ it will tend to zero, and so there will only be one bound state. The approximate solution is then ${\displaystyle v^{2}=u_{0}^{2}-u_{0}^{4}}$, and the energy tends to ${\displaystyle E=-mL^{2}V_{0}^{2}/2\hbar ^{2}}$. But this is just the energy of the bound state of a Delta function potential of strength ${\displaystyle V_{0}L}$, as it should be.

A simpler graphical solution for the energy levels can be obtained by normalizing the potential and the energy through multiplication by ${\displaystyle {8m}{L^{2}}/h^{2}}$. The normalized quantities are $${\displaystyle {\tilde {V}}_{0}=V_{0}{\frac {8m}{h^{2}}}L^{2}\qquad {\tilde {E}}=E{\frac {8m}{h^{2}}}L^{2}}$$ giving directly the relation between the allowed couples ${\displaystyle (V_{0},E)}$ as^[10] $${\displaystyle {\sqrt {{\tilde {V}}_{0}}}={\sqrt {\tilde {E}}}\,\left|{\sec({\sqrt {\tilde {E}}}\,{\pi }/{2})}\right|,\qquad {\sqrt {{\tilde {V}}_{0}}}={\sqrt {\tilde {E}}}\,\left|{\csc({\sqrt {\tilde {E}}}\,{\pi }/{2})}\right|}$$ for the even and odd parity wave functions, respectively. In the previous equations only the positive derivative parts of the functions have to be considered. The chart giving directly the allowed couples ${\displaystyle (V_{0},E)}$ is reported in the figure.

Consider a one-dimensional asymmetric potential well given by the potential^[11] $${\displaystyle V(x)={\begin{cases}V_{1},&{\text{if }}-\infty <x<0{\text{ (the region outside the well)}}\\0,&{\text{if }}0<x<a{\text{ (the region inside the well)}}\\V_{2}&{\text{if }}a<x<\infty {\text{ (the region outside the well)}}\end{cases}}}$$ with ${\displaystyle V_{2}>V_{1}}$. The corresponding solution for the wave function with ${\displaystyle E<V_{1}}$ is found to be $${\displaystyle \psi (x)={\begin{cases}c_{1}e^{k_{1}x},&{\text{for }}x<0,{\text{where }}k_{1}={\sqrt {(2m/\hbar ^{2})(V_{1}-E)}}\\c\sin(kx+\delta ),&{\text{for }}0<x<a,{\text{where }}k={\sqrt {2mE/\hbar ^{2}}}\\c_{2}e^{-k_{2}x},&{\text{for }}x>a,{\text{where }}k_{2}={\sqrt {(2m/\hbar ^{2})(V_{2}-E)}}\end{cases}}}$$ and $${\displaystyle \sin \delta ={\frac {k\hbar }{\sqrt {2mV_{1}}}}.}$$

The energy levels ${\displaystyle E=k^{2}\hbar ^{2}/(2m)}$ are determined once ${\displaystyle k}$ is solved as a root of the following transcendental equation $${\displaystyle ka=n\pi -\sin ^{-1}\left({\frac {k\hbar }{\sqrt {2mV_{1}}}}\right)-\sin ^{-1}\left({\frac {k\hbar }{\sqrt {2mV_{2}}}}\right)}$$ where ${\displaystyle n=1,2,3,\dots }$ Existence of root to above equation is not always guaranteed, for example, one can always find a value of ${\displaystyle a}$ so small, that for given values of ${\displaystyle V_{1}}$ and ${\displaystyle V_{2}}$, there exists no discrete energy level. The results of symmetrical well is obtained from above equation by setting ${\displaystyle V_{1}=V_{2}=V_{o}}$.

Consider the following spherical potential well $${\displaystyle U(r)={\begin{cases}-U_{0},&{\text{if }}r<a{\text{ (the region inside the well)}}\\0,&{\text{if }}r>a{\text{ (the region outside the well)}}\end{cases}}}$$ where ${\displaystyle r}$ is the radius from the origin. The solution for the wavefunction with zero angular momentum (${\displaystyle l=0}$) and with an energy ${\displaystyle E<0}$ is given by^[11] $${\displaystyle \psi (r)={\begin{cases}{\frac {A}{r}}\sin kr,&{\text{for }}r<a,{\text{where }}k={\sqrt {(2m/\hbar ^{2})(U_{0}-|E|)}}\\{\frac {B}{r}}e^{-\kappa r},&{\text{for }}r>a,{\text{where }}\kappa ={\sqrt {2m|E|/\hbar ^{2}}}={\sqrt {2mU_{0}/\hbar ^{2}-k^{2}}}.\end{cases}}}$$ satisfying the condition

${\displaystyle k\cot ka=-\kappa .}$

This equation does not always have a solution indicating that in some cases, there are no bound states. The minimum depth of the potential well for which the bound state first appears at ${\displaystyle E=0}$ is given by

${\displaystyle U_{0,\mathrm {min} }={\frac {\pi ^{2}\hbar ^{2}}{8ma^{2}}}}$

which increases with decreasing well radius ${\displaystyle a}$. Thus, bound states are not possible if the well is sufficiently shallow and narrow. For well depth slightly exceeding the minimum value, i.e., for ${\displaystyle U_{0}/U_{0,\mathrm {min} }-1\ll 1}$, the ground state energy ${\displaystyle E_{1}}$ (since we are considering ${\displaystyle l=0}$ case) is given by^[12]

${\displaystyle -E_{1}={\frac {\pi ^{2}}{16}}{\frac {(|U_{0}|-U_{0,\mathrm {min} })^{2}}{U_{0,\mathrm {min} }}}.}$

The results above can be used to show that, as to the one-dimensional case, there is two bound states in a spherical cavity, as spherical coordinates make equivalent the radius at any direction.

The ground state (n = 1) of a spherically symmetric potential will always have zero orbital angular momentum (ℓ = n−1), and the reduced wave function ${\displaystyle \chi (r)\equiv r\psi (r)}$ satisfies the equation $${\displaystyle -{\frac {\hbar ^{2}}{2m}}{\frac {d^{2}\chi }{dr^{2}}}+U(r)\chi (r)=E\chi (r)}$$ where ${\displaystyle \psi (r)}$ is the radial part of the wave function. Notice that for (n = 1) angular part is constant (ℓ = 0).

This is identical to the one-dimensional equation, except for the boundary conditions. As before, $${\displaystyle \chi (r)={\begin{cases}c_{1}\sin({k_{1}r}),&{\text{for }}r<a,{\text{ where }}k_{1}={\sqrt {2m/\hbar ^{2}(U_{1}-E)}}\\[1ex]c\sin({kr+\delta }),&{\text{for }}a<r<b,{\text{ where }}k={\sqrt {2mE/\hbar ^{2}}}\\[1ex]c_{2}e^{-k_{2}r},&{\text{for }}r>b,{\text{ where }}k_{2}={\sqrt {2m/\hbar ^{2}(U_{2}-E)}}\end{cases}}}$$

The energy levels for ${\displaystyle a<r<b}$ $${\displaystyle E={\frac {k^{2}\hbar ^{2}}{2m}}}$$ are determined once ${\displaystyle {\displaystyle k}}$ is solved as a root of the following transcendental equation $${\displaystyle k(b-a)=n\pi }$$ where ${\displaystyle {\displaystyle n=1,2,3,\dots }}$

Existence of root to above equation is always guaranteed. The results are always with spherical symmetry. It fulfils the condition where the wave does not find any potential inside the sphere: ${\displaystyle \chi (a)=\chi (0)=0}$.

Different differential equation lay on when ℓ ≠0, so as above titles, here it is: $${\displaystyle {\frac {d^{2}\chi }{dr^{2}}}+{\begin{Bmatrix}k^{2}-{\frac {l(l+1)}{r^{2}}}\end{Bmatrix}}\chi (r)=0}$$

The solution can be rationalized by some changes of variable and function to rise a Bessel like differential equation, which solution is: $${\displaystyle {\frac {\chi (r)}{r}}={\begin{cases}Aj_{l}({k_{1}r}),&{\text{for }}r<a,{\text{ where }}k_{1}={\sqrt {2m/\hbar ^{2}(U_{1}-E)}}\\[1ex]Aj_{l}({kr})+By_{l}({kr}),&{\text{for }}a<r<b,{\text{ where }}k={\sqrt {2mE/\hbar ^{2}}}\\[1ex]Ch_{l}^{(1)}({k_{2}r}),&{\text{for }}r>b,{\text{ where }}k_{2}={\sqrt {2m/\hbar ^{2}(U_{2}-E)}}\end{cases}}}$$ where ${\displaystyle j_{l}{(kr)}}$, ${\displaystyle y_{l}({kr})}$ and ${\displaystyle h_{l}^{(1)}({kr})}$ are Bessel, Newman and Hankel spherical functions respectively, and could be rewritten as function of standard Bessel function.

The energy levels for ${\displaystyle a<r<b}$ $${\displaystyle E={\frac {k^{2}\hbar ^{2}}{2m}}}$$ are determined once ${\displaystyle {\displaystyle k}}$ is solved as a root of the following transcendental equation $${\displaystyle k(b-a)={\frac {4n\pi }{2\ell +1}}}$$ where ${\displaystyle n=1,2,3,\dots }$

Also this two transcendental equations are ${\displaystyle {\displaystyle k}}$ solutions: $${\displaystyle kb={\frac {n\pi }{2\ell +1}}{\begin{Bmatrix}3-2\sin ^{2}\left(\pi {\frac {\ell +1}{2}}\right)\end{Bmatrix}}}$$ and also, $${\displaystyle ka={\frac {n\pi }{2\ell +1}}{\begin{Bmatrix}3-2\sin ^{2}\left(\pi {\frac {\ell +1}{2}}\right)\end{Bmatrix}}}$$

Existence of roots to above equations are always guaranteed. The results are always with spherical symmetry.

• Potential well
• Delta function potential
• Infinite potential well
• Semicircle potential well
• Quantum tunnelling
• Rectangular potential barrier