Recent from talks
Contribute something
Nothing was collected or created yet.
Moore machine
View on WikipediaThis article needs additional citations for verification. (November 2024) |
In the theory of computation, a Moore machine is a finite-state machine whose current output values are determined only by its current state. This is in contrast to a Mealy machine, whose output values are determined both by its current state and by the values of its inputs. Like other finite state machines, in Moore machines, the input typically influences the next state. Thus the input may indirectly influence subsequent outputs, but not the current or immediate output. The Moore machine is named after Edward F. Moore, who presented the concept in a 1956 paper, “Gedanken-experiments on Sequential Machines.”[1]
Formal definition
[edit]A Moore machine can be defined as a 6-tuple consisting of the following:
- A finite set of states
- A start state (also called initial state) which is an element of
- A finite set called the input alphabet
- A finite set called the output alphabet
- A transition function mapping a state and the input alphabet to the next state
- An output function mapping each state to the output alphabet
"Evolution across time" is realized in this abstraction by having the state machine consult the time-changing input symbol at discrete "timer ticks" and react according to its internal configuration at those idealized instants, or else having the state machine wait for a next input symbol (as on a FIFO) and react whenever it arrives.
A Moore machine can be regarded as a restricted type of finite-state transducer.
Visual representation
[edit]Table
[edit]A state transition table is a table listing all the triples in the transition relation .
Diagram
[edit]The state diagram for a Moore machine, or Moore diagram, is a state diagram that associates an output value with each state.
Relationship with Mealy machines
[edit]As Moore and Mealy machines are both types of finite-state machines, they are equally expressive: either type can be used to parse a regular language.
The difference between Moore machines and Mealy machines is that in the latter, the output of a transition is determined by the combination of current state and current input ( as the domain of ), as opposed to just the current state ( as the domain of ). When represented as a state diagram,
- for a Moore machine, each node (state) is labeled with an output value;
- for a Mealy machine, each arc (transition) is labeled with an output value.
Every Moore machine is equivalent to the Mealy machine with the same states and transitions and the output function , which takes each state-input pair and yields , where is 's output function and is 's transition function.
However, not every Mealy machine can be converted to an equivalent Moore machine. Some can be converted only to an almost equivalent Moore machine, with outputs shifted in time. This is due to the way that state labels are paired with transition labels to form the input/output pairs. Consider a transition from state to state . The input causing the transition labels the edge . The output corresponding to that input, is the label of state .[2] Notice that this is the source state of the transition. So for each input, the output is already fixed before the input is received, and depends solely on the present state. This is the original definition by E. Moore. It is a common mistake to use the label of state as output for the transition .
Examples
[edit]Types according to number of inputs/outputs.
Simple
[edit]Simple Moore machines have one input and one output:
- edge detector using XOR
- binary adding machine
- clocked sequential systems (a restricted form of Moore machine where the state changes only when the global clock signal changes)
Most digital electronic systems are designed as clocked sequential systems. Clocked sequential systems are a restricted form of Moore machine where the state changes only when the global clock signal changes. Typically the current state is stored in flip-flops, and a global clock signal is connected to the "clock" input of the flip-flops. Clocked sequential systems are one way to solve metastability problems. A typical electronic Moore machine includes a combinational logic chain to decode the current state into the outputs (lambda). The instant the current state changes, those changes ripple through that chain, and almost instantaneously the output gets updated. There are design techniques to ensure that no glitches occur on the outputs during that brief period while those changes are rippling through the chain, but most systems are designed so that glitches during that brief transition time are ignored or are irrelevant. The outputs then stay the same indefinitely (LEDs stay bright, power stays connected to the motors, solenoids stay energized, etc.), until the Moore machine changes state again.
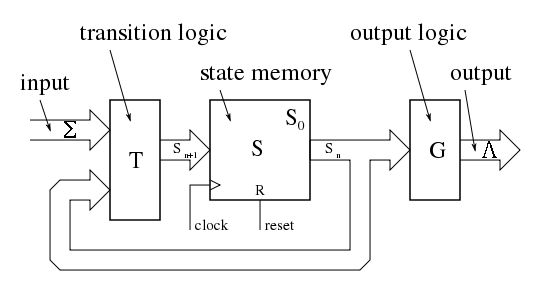
Worked example
[edit]A sequential network has one input and one output. The output becomes 1 and remains 1 thereafter when at least two 0's and two 1's have occurred as inputs.

A Moore machine with nine states for the above description is shown on the right. The initial state is state A, and the final state is state I. The state table for this example is as follows:
| Current state | Input | Next state | Output |
|---|---|---|---|
| A | 0 | D | 0 |
| 1 | B | ||
| B | 0 | E | 0 |
| 1 | C | ||
| C | 0 | F | 0 |
| 1 | C | ||
| D | 0 | G | 0 |
| 1 | E | ||
| E | 0 | H | 0 |
| 1 | F | ||
| F | 0 | I | 0 |
| 1 | F | ||
| G | 0 | G | 0 |
| 1 | H | ||
| H | 0 | H | 0 |
| 1 | I | ||
| I | 0 | I | 1 |
| 1 | I |
Complex
[edit]More complex Moore machines can have multiple inputs as well as multiple outputs.
Gedanken-experiments
[edit]In Moore's 1956 paper "Gedanken-experiments on Sequential Machines",[1] the automata (or machines) are defined as having states, input symbols and output symbols. Nine theorems are proved about the structure of , and experiments with . Later, " machines" became known as "Moore machines".
At the end of the paper, in Section "Further problems", the following task is stated:
Another directly following problem is the improvement of the bounds given at the theorems 8 and 9.
Moore's Theorem 8 is formulated as:
Given an arbitrary machine , such that every two of its states are distinguishable from one another, then there exists an experiment of length which determines the state of at the end of the experiment.
In 1957, A. A. Karatsuba proved the following two theorems, which completely solved Moore's problem on the improvement of the bounds of the experiment length of his "Theorem 8".
Theorem A. If is an machine, such that every two of its states are distinguishable from one another, then there exists a branched experiment of length at most through which one may determine the state of at the end of the experiment.
Theorem B. There exists an machine, every two states of which are distinguishable from one another, such that the length of the shortest experiments establishing the state of the machine at the end of the experiment is equal to .
Theorems A and B were used for the basis of the course work of a student of the fourth year, A. A. Karatsuba, "On a problem from the automata theory", which was distinguished by testimonial reference at the competition of student works of the faculty of mechanics and mathematics of Moscow State University in 1958. The paper by Karatsuba was given to the journal Uspekhi Mat. Nauk on 17 December 1958 and was published there in June 1960.[3]
Until the present day (2011), Karatsuba's result on the length of experiments is the only exact nonlinear result, both in automata theory, and in similar problems of computational complexity theory.
See also
[edit]References
[edit]- ^ a b Moore, Edward F (1956). "Gedanken-experiments on Sequential Machines". Automata Studies, Annals of Mathematical Studies (34). Princeton, N.J.: Princeton University Press: 129–153.
- ^ Lee, Edward Ashford; Seshia, Sanjit Arunkumar (2013). Introduction to Embedded Systems (1.08 ed.). UC Berkeley: Lulu.com. ISBN 9780557708574. Retrieved 1 July 2014.
- ^ Karatsuba, A. A. (1960). "Solution of one problem from the theory of finite automata". Uspekhi Mat. Nauk (15:3): 157–159.
Further reading
[edit]- Conway, J.H. (1971). Regular algebra and finite machines. London: Chapman and Hall. ISBN 0-412-10620-5. Zbl 0231.94041.
- Moore E. F. Gedanken-experiments on Sequential Machines. Automata Studies, Annals of Mathematical Studies, 34, 129–153. Princeton University Press, Princeton, N.J.(1956).
- Karatsuba A. A. Solution of one problem from the theory of finite automata. Usp. Mat. Nauk, 15:3, 157–159 (1960).
- Karatsuba A. A. Experimente mit Automaten (German) Elektron. Informationsverarb. Kybernetik, 11, 611–612 (1975).
- Karatsuba A. A. List of research works.
External links
[edit] Media related to Moore machine at Wikimedia Commons
Media related to Moore machine at Wikimedia Commons
Moore machine
View on GrokipediaIntroduction
Overview
A Moore machine is a type of finite-state machine (FSM) in which the outputs are determined solely by the current state of the machine, independent of the input symbols received.[3] This model contrasts with other FSM variants by decoupling output generation from immediate input processing, allowing the machine to produce consistent responses based on its internal configuration.[1] Moore machines are widely used to model sequential behavior in various systems, including digital circuits for control logic and software for reactive processes.[1] In digital hardware, they facilitate the design of synchronous circuits where states are stored in flip-flops, enabling reliable operation in applications like counters and protocol controllers.[3] In software, they support the specification of state-driven behaviors in embedded systems and user interfaces.[1] Within the broader framework of automata theory, Moore machines position themselves as an extension of deterministic finite automata (DFAs), which form a subset lacking explicit outputs but sharing the deterministic state transition properties.[3] Key advantages of this model include simpler output logic, since outputs map directly to states without input dependencies, and glitch-free outputs in hardware implementations, as changes occur only upon synchronous state updates.[3][4]Historical Background
The Moore machine, a fundamental model in automata theory, was introduced by Edward F. Moore in his seminal 1956 paper "Gedanken-Experiments on Sequential Machines," published in the edited volume Automata Studies. This work formalized the concept of a sequential machine where outputs depend solely on the current state, distinguishing it from earlier informal descriptions of sequential behavior in computational devices. Moore's contribution built on experimental thought processes to explore the capabilities and limitations of finite-state systems, laying groundwork for abstract modeling of computation. The development of the Moore machine occurred amid mid-20th-century advancements in switching theory and computability during the 1940s and 1950s, heavily influenced by pioneers such as Claude Shannon and Warren McCulloch. Shannon's 1938 master's thesis, "A Symbolic Analysis of Relay and Switching Circuits," established the application of Boolean algebra to electrical switching, providing a mathematical basis for analyzing circuit behavior that extended to sequential logic.[5] Complementing this, McCulloch and Pitts's 1943 paper, "A Logical Calculus of the Ideas Immanent in Nervous Activity," modeled neural activity as binary threshold devices, inspiring formal models of automata that bridged biology, logic, and computation. These influences converged in the post-World War II era, as researchers sought rigorous frameworks for understanding information processing in both theoretical and practical systems.[6] The Moore machine evolved from early 20th-century relay-based sequential circuits, which powered electromechanical computers like the Harvard Mark I in the 1940s, toward abstracted formal models in the 1950s and 1960s. Initial relay designs relied on physical components for state memory and transitions, but the shift to symbolic and mathematical representations in switching theory enabled scalable analysis of complex behaviors without hardware constraints.[7] By the mid-1950s, works like George H. Mealy's 1955 paper on sequential circuit synthesis paralleled Moore's efforts, formalizing state-dependent outputs in a way that supported minimization and optimization techniques.[8] Initially, Moore machines found applications in theoretical computer science for studying finite automata and regular languages, contributing to the foundational principles of computability explored in Automata Studies.[6] In early digital design, they informed the synthesis of reliable sequential circuits for emerging electronic computers, aiding engineers in predicting and verifying system responses to inputs. This dual role underscored their impact in bridging abstract theory with practical circuit engineering during the formative years of digital technology.Formal Definition
Mathematical Model
A Moore machine is formally defined as a six-tuple , where is a finite set of states, is a finite input alphabet, is a finite output alphabet, is the transition function, is the output function, and is the initial state.[9] This model, introduced by Edward F. Moore, captures the behavior of sequential systems where outputs are associated solely with states. The transition function ensures determinism: for every state and input symbol , there is exactly one next state .[9] This property guarantees that the machine's evolution is uniquely determined by the initial state and the sequence of inputs, without nondeterminism. Given an input string , the machine generates an output string by iteratively applying the transition and output functions. Starting from , the state sequence is , where for , and the corresponding output string is .[9] Note that the output sequence has length , including an initial output before any input is processed. The output independence from the immediate input follows directly from the structure of , which maps only the current state to an output symbol, without reference to the current input. To see this, consider the output at step : it is , where depends on the history of prior inputs and states up to , but not on . Thus, even if varies while keeping prior history fixed, remains unchanged, ensuring is invariant to . This contrasts with input-dependent output models and underscores the state-centric nature of Moore machines.[9]Components and Functions
A Moore machine is defined by a finite set of states , which represents the distinct configurations or conditions the system can be in during operation. This set includes an initial state , from which the machine begins processing inputs. Each state encapsulates the relevant history of prior inputs necessary for determining future behavior, ensuring the machine's memory is finite and discrete. The input alphabet consists of a finite collection of symbols that serve as the external stimuli to the machine. These symbols trigger changes in the machine's state but do not directly influence the output; instead, they determine how the system evolves over time.[10] The output alphabet is another finite set, comprising the possible output symbols that the machine produces in response to its internal state. Outputs are generated solely based on the current state, independent of the immediate input, which distinguishes the Moore model from others. The transition function specifies the deterministic behavior of state changes, mapping each pair consisting of a current state and an input symbol to a unique next state. Formally, it is defined as , ensuring that for any and , where is the resulting state. This function guarantees predictable progression without ambiguity.[10] The output function associates each state with an output symbol, producing the machine's response exclusively from the state information. It is given by , such that for any state , where . This state-dependent output generation emphasizes the machine's reliance on accumulated context rather than instantaneous inputs.Representations
State Diagrams
State diagrams offer a visual method to represent Moore machines, illustrating the finite set of states and the transitions between them triggered by inputs, with outputs explicitly tied to states. In this graphical notation, each state is depicted as a circle, and the output value for that state is written inside the circle, reflecting the Moore machine's defining property that outputs depend solely on the current state rather than the input. Directed arcs connect the circles to show transitions, with each arc labeled by the input symbol(s) that cause the machine to move from one state to another.[1][11] A key rule for constructing these diagrams is that every state produces exactly one output, ensuring the representation captures the machine's synchronous behavior where state changes occur on clock edges, and outputs are stable within each state. Transitions are determined by the input and current state, leading to a next state without altering the output labeling on the arcs themselves. The initial state is commonly distinguished by a double circle or an incoming arrow from a small filled circle, providing a clear entry point for tracing the machine's operation from startup. Solid lines are typically used for the directed arcs to emphasize the deterministic flow.[11][1] This diagrammatic approach excels in intuitiveness, allowing designers and analysts to readily observe the direct linkage between states and outputs, as well as detect cycles or loops that indicate repetitive behaviors in the machine. For instance, a generic unlabeled state diagram might feature three states labeled as A, B, and C, with outputs 0 inside A and B, and 1 inside C; transitions could include an arc from A to B on input 0, from A to C on input 1, from B to A on input 1, and self-loops on B for input 0, all connected by directed arrows to highlight the structural flow without specific contextual application. Such visualizations facilitate qualitative understanding of the machine's dynamics, distinguishing them from tabular forms by emphasizing topological relationships over exhaustive listings.[1][11]Transition Tables
Transition tables provide a tabular representation of a Moore machine, systematically enumerating the behavior defined by its transition function δ and output function λ. In this format, rows correspond to the current states in the finite set Q, while columns represent the possible input symbols from the alphabet Σ. Each cell at the intersection of a current state q and input σ specifies the next state δ(q, σ). Since outputs in a Moore machine depend solely on the current state via λ(q), they are typically listed in a dedicated column aligned with each state row or in a separate output table mapping states to their outputs.[12][13] To construct a transition table, first identify all states Q and inputs Σ, ensuring coverage of the complete Cartesian product Q × Σ for exhaustive enumeration. Assign symbolic or binary encodings to states if needed for implementation. Then, populate the table by deriving entries from the machine's specification, such as a state diagram: for each current state q and input σ, enter the resulting next state δ(q, σ) in the appropriate cell, and append the output λ(q) in the state-specific output column. This process yields a complete, deterministic table that captures the machine's dynamics without ambiguity.[13][14] The use of transition tables offers several advantages, including their exhaustive nature, which ensures all possible state-input combinations are explicitly defined, aiding in error detection and formal verification. They also facilitate straightforward simulation by allowing sequential traversal of the table based on input sequences, as well as the application of minimization algorithms that partition equivalent states for reduced complexity. Additionally, the separation of outputs tied to states simplifies logic synthesis in hardware implementations, as output combinational circuits depend only on state variables.[12][13] For machines with multiple outputs, the output column in each state row lists the output tuple λ(q) = (o_1, o_2, ..., o_m), where each o_i is a symbol from the output alphabet Γ, or separate columns can be used for each output bit to clarify binary encodings. Transition tables can be derived from state diagrams to provide a discrete, data-oriented alternative for analysis.[12] A blank template for a Moore machine transition table with binary inputs might appear as follows:| Current State | Output | Input 0 (Next State) | Input 1 (Next State) |
|---|---|---|---|
| q_0 | |||
| q_1 | |||
| ... |
Comparison with Mealy Machines
Key Differences
The fundamental difference between Moore and Mealy machines resides in their output generation mechanisms. In a Moore machine, outputs are exclusively a function of the current state, expressed mathematically as the output function , where denotes the finite set of states and the output alphabet.[15] Conversely, in a Mealy machine, outputs depend on both the current state and the current input, formalized as , with representing the input alphabet.[16] This structural variance leads to distinct timing behaviors in synchronous implementations. Moore machine outputs stabilize one clock cycle after an input arrives, as they are registered and change only upon state transitions at the clock edge, promoting glitch-free operation. Consequently, for a sequence of n inputs, Moore machines produce n+1 outputs, starting with the initial state's output, whereas Mealy machines produce n outputs, one per input.[15] Mealy machine outputs, generated combinationaly, respond immediately to inputs but may exhibit glitches due to concurrent signal propagation delays.[17] Mealy machines generally require fewer states to achieve equivalent functionality, since their output logic can leverage input values directly on transitions, reducing the need for dedicated output-encoding states.[16] Moore machines often necessitate additional states to maintain output stability across input variations, potentially increasing hardware complexity in state representation.[15] From an implementation perspective, Moore machines simplify output logic design, as outputs derive solely from state variables via straightforward combinational decoding, aiding modularity and verification.[17] Mealy machines demand more intricate combinational circuits incorporating both state and input terms, though this enables quicker overall response at the cost of elevated design effort.[16] These differences manifest in behavioral traces for identical input sequences. For instance, given inputs 1 followed by 0 in a basic two-state machine starting from an initial state, a Moore machine might yield outputs 0 (initial) then 1 (after transition on second clock), reflecting delayed response; a Mealy machine could produce 0 then 1 immediately on the transition triggered by the second input, highlighting the instantaneous output adjustment.[15]Model Conversion
Model conversion between Moore and Mealy machines ensures functional equivalence while adapting the output generation mechanism, preserving the input-output behavior (transduction function) of the machine but adjusting for the timing of outputs, where Moore machines produce outputs based on the current state after a transition, effectively delaying output by one step relative to input changes compared to Mealy machines.[18] To convert a Moore machine to a Mealy machine, retain all states and transitions from the original model, then assign to each transition the output associated with its target state, labeling arcs with input symbols and the corresponding output from the destination state.[18] This process may allow state merging if equivalent behaviors emerge, potentially reducing the number of states, and simplifies output logic by integrating it directly with transition functions.[19] Conversely, converting a Mealy machine to a Moore machine requires splitting states where outgoing transitions produce differing outputs, creating new states for each unique (next-state, output) pair to ensure outputs depend solely on states.[20] The algorithm proceeds as follows: (1) identify all distinct pairs of next states and their associated outputs from the transition table; (2) introduce a new state for each such pair, appending the output to the state identifier; (3) update transitions to point to these new states; (4) add output functions to the new states and propagate original state outputs to split instances.[20] This conversion often increases the number of states, as each original state may fragment based on output variations, but it decouples outputs from inputs for potentially more stable designs.[19] In both directions, equivalence is maintained by verifying that the converted machine produces the same output sequence for any input string, though the one-step delay in Moore outputs must be accounted for in timing-sensitive applications.[18] The algorithmic outline generally involves detecting output inconsistencies or consistencies across transitions or states: for Moore to Mealy, collapse where possible by unifying outputs on arcs; for Mealy to Moore, insert intermediate states at points of output divergence to resolve dependencies on inputs.[20]Examples
Basic Example
A simple illustrative example of a Moore machine is a controller for a toggle light switch, where a binary input signal (0 or 1) determines whether the light state changes. The machine has two states: Off (light is off) and On (light is on), with the initial state being Off. This setup demonstrates the core principles of state-based output generation without direct input dependency on outputs.[21] The transition function δ is defined such that an input of 0 leaves the current state unchanged (no toggle), while an input of 1 switches to the opposite state. Specifically: δ(Off, 0) = Off, δ(Off, 1) = On; δ(On, 0) = On, δ(On, 1) = Off. The output function λ produces 0 (light off) in the Off state and 1 (light on) in the On state, ensuring the output reflects only the current state. The following transition table summarizes the behavior:| Current State | Input | Next State | Output |
|---|---|---|---|
| Off | 0 | Off | 0 |
| Off | 1 | On | 0 |
| On | 0 | On | 1 |
| On | 1 | Off | 1 |
Sequence Detector
A sequence detector is a common application of the Moore machine in digital systems, designed to identify a specific pattern in a serial binary input stream and produce an output signal upon detection. In this example, the machine detects the binary sequence "101" with allowance for overlapping occurrences, meaning that the ending portion of one detected sequence can serve as the beginning of another. The output is 1 when the machine enters the state corresponding to the completion of the sequence and 0 otherwise, providing a pulse indication at the clock cycle following the final bit of the match.[22] The Moore machine for this detector uses four states to track the progress toward matching "101":- S0: Initial or reset state, representing no relevant prefix of the sequence observed.
- S1: The input stream ends with "1", matching the first bit of the sequence.
- S2: The input stream ends with "10", matching the first two bits.
- S3: The input stream ends with "101", indicating a match (accepting state).
| Current State | Input 0 | Input 1 |
|---|---|---|
| S0 | S0 | S1 |
| S1 | S2 | S1 |
| S2 | S0 | S3 |
| S3 | S2 | S1 |
- After first bit (1): Transition to S1, output 0.
- After second bit (1): From S1 to S1 (ends with "11"), output 0.
- After third bit (0): From S1 to S2 (ends with "110"), output 0.
- After fourth bit (1): From S2 to S3 (ends with "1101", matching "101" at positions 2–4), output 1 (detection at position 4).
- After fifth bit (0): From S3 to S2 (ends with "11010"), output 0.
- After sixth bit (1): From S2 to S3 (ends with "110101", matching "101" at positions 4–6, overlapping the previous), output 1 (detection at position 6).


























