Recent from talks
Nothing was collected or created yet.
Boolean algebra
View on Wikipedia
In mathematics and mathematical logic, Boolean algebra is a branch of algebra. It differs from elementary algebra in two ways. First, the values of the variables are the truth values true and false, usually denoted by 1 and 0, whereas in elementary algebra the values of the variables are numbers. Second, Boolean algebra uses logical operators such as conjunction (and) denoted as ∧, disjunction (or) denoted as ∨, and negation (not) denoted as ¬. Elementary algebra, on the other hand, uses arithmetic operators such as addition, multiplication, subtraction, and division. Boolean algebra is therefore a formal way of describing logical operations in the same way that elementary algebra describes numerical operations.
Boolean algebra was introduced by George Boole in his first book The Mathematical Analysis of Logic (1847),[1] and set forth more fully in his An Investigation of the Laws of Thought (1854).[2] According to Huntington, the term Boolean algebra was first suggested by Henry M. Sheffer in 1913,[3] although Charles Sanders Peirce gave the title "A Boolian [sic] Algebra with One Constant" to the first chapter of his "The Simplest Mathematics" in 1880.[4] Boolean algebra has been fundamental in the development of digital electronics, and is provided for in all modern programming languages. It is also used in set theory and statistics.[5]
History
[edit]A precursor of Boolean algebra was Gottfried Wilhelm Leibniz's algebra of concepts. The usage of binary in relation to the I Ching was central to Leibniz's characteristica universalis. It eventually created the foundations of algebra of concepts.[6] Leibniz's algebra of concepts is deductively equivalent to the Boolean algebra of sets.[7]
Boole's algebra predated the modern developments in abstract algebra and mathematical logic; it is however seen as connected to the origins of both fields.[8] In an abstract setting, Boolean algebra was perfected in the late 19th century by Jevons, Schröder, Huntington and others, until it reached the modern conception of an (abstract) mathematical structure.[8] For example, the empirical observation that one can manipulate expressions in the algebra of sets, by translating them into expressions in Boole's algebra, is explained in modern terms by saying that the algebra of sets is a Boolean algebra (note the indefinite article). In fact, M. H. Stone proved in 1936 that every Boolean algebra is isomorphic to a field of sets.[9][10]
In the 1930s, while studying switching circuits, Claude Shannon observed that one could also apply the rules of Boole's algebra in this setting,[11] and he introduced switching algebra as a way to analyze and design circuits by algebraic means in terms of logic gates. Shannon already had at his disposal the abstract mathematical apparatus, thus he cast his switching algebra as the two-element Boolean algebra. In modern circuit engineering settings, there is little need to consider other Boolean algebras, thus "switching algebra" and "Boolean algebra" are often used interchangeably.[12][13][14]
Efficient implementation of Boolean functions is a fundamental problem in the design of combinational logic circuits. Modern electronic design automation tools for very-large-scale integration (VLSI) circuits often rely on an efficient representation of Boolean functions known as (reduced ordered) binary decision diagrams (BDD) for logic synthesis and formal verification.[15]
Logic sentences that can be expressed in classical propositional calculus have an equivalent expression in Boolean algebra. Thus, Boolean logic is sometimes used to denote propositional calculus performed in this way.[16][17][18] Boolean algebra is not sufficient to capture logic formulas using quantifiers, like those from first-order logic.
Although the development of mathematical logic did not follow Boole's program, the connection between his algebra and logic was later put on firm ground in the setting of algebraic logic, which also studies the algebraic systems of many other logics.[8] The problem of determining whether the variables of a given Boolean (propositional) formula can be assigned in such a way as to make the formula evaluate to true is called the Boolean satisfiability problem (SAT), and is of importance to theoretical computer science, being the first problem shown to be NP-complete. The closely related model of computation known as a Boolean circuit relates time complexity (of an algorithm) to circuit complexity.
Values
[edit]Whereas expressions denote mainly numbers in elementary algebra, in Boolean algebra, they denote the truth values false and true. These values are represented with the bits, 0 and 1. They do not behave like the integers 0 and 1, for which 1 + 1 = 2, but may be identified with the elements of the two-element field GF(2), that is, integer arithmetic modulo 2, for which 1 + 1 = 0. Addition and multiplication then play the Boolean roles of XOR (exclusive-or) and AND (conjunction), respectively, with disjunction x ∨ y (inclusive-or) definable as x + y − xy and negation ¬x as 1 − x. In GF(2), − may be replaced by +, since they denote the same operation; however, this way of writing Boolean operations allows applying the usual arithmetic operations of integers (this may be useful when using a programming language in which GF(2) is not implemented).
Boolean algebra also deals with functions which have their values in the set {0,1}. A sequence of bits is a commonly used example of such a function. Another common example is the totality of subsets of a set E: to a subset F of E, one can define the indicator function that takes the value 1 on F, and 0 outside F. The most general example is the set elements of a Boolean algebra, with all of the foregoing being instances thereof.
As with elementary algebra, the purely equational part of the theory may be developed, without considering explicit values for the variables.[19]
Operations
[edit]This section needs additional citations for verification. (April 2019) |
Basic operations
[edit]While elementary algebra has four operations (addition, subtraction, multiplication, and division), the Boolean algebra has only three basic operations: conjunction, disjunction, and negation, expressed with the corresponding binary operators AND () and OR () and the unary operator NOT (), collectively referred to as Boolean operators.[20] Variables in Boolean algebra that store the logical value of 0 and 1 are called the Boolean variables. They are used to store either true or false values.[21] The basic operations on Boolean variables x and y are defined as follows:
|
Alternatively, the values of x ∧ y, x ∨ y, and ¬x can be expressed by tabulating their values with truth tables as follows:[22]
|
|
When used in expressions, the operators are applied according to the precedence rules. As with elementary algebra, expressions in parentheses are evaluated first, following the precedence rules.[23]
If the truth values 0 and 1 are interpreted as integers, these operations may be expressed with the ordinary operations of arithmetic (where x + y uses addition and xy uses multiplication), or by the minimum/maximum functions:
One might consider that only negation and one of the two other operations are basic because of the following identities that allow one to define conjunction in terms of negation and the disjunction, and vice versa (De Morgan's laws):[24]
Secondary operations
[edit]Operations composed from the basic operations include, among others, the following:
| Material conditional: | |
| Material biconditional: | |
| Exclusive OR (XOR): |
These definitions give rise to the following truth tables giving the values of these operations for all four possible inputs.
Secondary operations. Table 1 0 0 1 0 1 1 0 0 1 0 0 1 1 1 0 1 1 1 0 1
- Material conditional
- The first operation, x → y, or Cxy, is called material implication. If x is true, then the result of expression x → y is taken to be that of y (e.g. if x is true and y is false, then x → y is also false). But if x is false, then the value of y can be ignored; however, the operation must return some Boolean value and there are only two choices. So by definition, x → y is true when x is false (relevance logic rejects this definition, by viewing an implication with a false premise as something other than either true or false).
- Exclusive OR (XOR)
- The second operation, x ⊕ y, or Jxy, is called exclusive or (often abbreviated as XOR) to distinguish it from disjunction as the inclusive kind. It excludes the possibility of both x and y being true (e.g. see table): if both are true then result is false. Defined in terms of arithmetic it is addition where mod 2 is 1 + 1 = 0.
- Logical equivalence
- The third operation, the complement of exclusive or, is equivalence or Boolean equality: x ≡ y, or Exy, is true just when x and y have the same value. Hence x ⊕ y as its complement can be understood as x ≠ y, being true just when x and y are different. Thus, its counterpart in arithmetic mod 2 is x + y. Equivalence's counterpart in arithmetic mod 2 is x + y + 1.
Laws
[edit]A law of Boolean algebra is an identity such as x ∨ (y ∨ z) = (x ∨ y) ∨ z between two Boolean terms, where a Boolean term is defined as an expression built up from variables and the constants 0 and 1 using the operations ∧, ∨, and ¬. The concept can be extended to terms involving other Boolean operations such as ⊕, →, and ≡, but such extensions are unnecessary for the purposes to which the laws are put. Such purposes include the definition of a Boolean algebra as any model of the Boolean laws, and as a means for deriving new laws from old as in the derivation of x ∨ (y ∧ z) = x ∨ (z ∧ y) from y ∧ z = z ∧ y (as treated in § Axiomatizing Boolean algebra).
Monotone laws
[edit]Boolean algebra satisfies many of the same laws as ordinary algebra when one matches up ∨ with addition and ∧ with multiplication. In particular the following laws are common to both kinds of algebra:[25][26]
Associativity of ∨: Associativity of ∧: Commutativity of ∨: Commutativity of ∧: Distributivity of ∧ over ∨: Identity for ∨: Identity for ∧: Annihilator for ∧:
The following laws hold in Boolean algebra, but not in ordinary algebra:
Annihilator for ∨: Idempotence of ∨: Idempotence of ∧: Absorption 1: Absorption 2: Distributivity of ∨ over ∧:
Taking x = 2 in the third law above shows that it is not an ordinary algebra law, since 2 × 2 = 4. The remaining five laws can be falsified in ordinary algebra by taking all variables to be 1. For example, in absorption law 1, the left hand side would be 1(1 + 1) = 2, while the right hand side would be 1 (and so on).
All of the laws treated thus far have been for conjunction and disjunction. These operations have the property that changing either argument either leaves the output unchanged, or the output changes in the same way as the input. Equivalently, changing any variable from 0 to 1 never results in the output changing from 1 to 0. Operations with this property are said to be monotone. Thus the axioms thus far have all been for monotonic Boolean logic. Nonmonotonicity enters via complement ¬ as follows.[5]
Nonmonotone laws
[edit]The complement operation is defined by the following two laws.
All properties of negation including the laws below follow from the above two laws alone.[5]
In both ordinary and Boolean algebra, negation works by exchanging pairs of elements, hence in both algebras it satisfies the double negation law (also called involution law)
But whereas ordinary algebra satisfies the two laws
Boolean algebra satisfies De Morgan's laws:
Completeness
[edit]The laws listed above define Boolean algebra, in the sense that they entail the rest of the subject. The laws complementation 1 and 2, together with the monotone laws, suffice for this purpose and can therefore be taken as one possible complete set of laws or axiomatization of Boolean algebra. Every law of Boolean algebra follows logically from these axioms. Furthermore, Boolean algebras can then be defined as the models of these axioms as treated in § Boolean algebras.
Writing down further laws of Boolean algebra cannot give rise to any new consequences of these axioms, nor can it rule out any model of them. In contrast, in a list of some but not all of the same laws, there could have been Boolean laws that did not follow from those on the list, and moreover there would have been models of the listed laws that were not Boolean algebras.
This axiomatization is by no means the only one, or even necessarily the most natural given that attention was not paid as to whether some of the axioms followed from others, but there was simply a choice to stop when enough laws had been noticed, treated further in § Axiomatizing Boolean algebra. Or the intermediate notion of axiom can be sidestepped altogether by defining a Boolean law directly as any tautology, understood as an equation that holds for all values of its variables over 0 and 1.[27][28] All these definitions of Boolean algebra can be shown to be equivalent.
Duality principle
[edit]Principle: If {X, R} is a partially ordered set, then {X, R(inverse)} is also a partially ordered set.
There is nothing special about the choice of symbols for the values of Boolean algebra. 0 and 1 could be renamed to α and β, and as long as it was done consistently throughout, it would still be Boolean algebra, albeit with some obvious cosmetic differences.
But suppose 0 and 1 were renamed 1 and 0 respectively. Then it would still be Boolean algebra, and moreover operating on the same values. However, it would not be identical to our original Boolean algebra because now ∨ behaves the way ∧ used to do and vice versa. So there are still some cosmetic differences to show that the notation has been changed, despite the fact that 0s and 1s are still being used.
But if in addition to interchanging the names of the values, the names of the two binary operations are also interchanged, now there is no trace of what was done. The end product is completely indistinguishable from what was started with. The columns for x ∧ y and x ∨ y in the truth tables have changed places, but that switch is immaterial.
When values and operations can be paired up in a way that leaves everything important unchanged when all pairs are switched simultaneously, the members of each pair are called dual to each other. Thus 0 and 1 are dual, and ∧ and ∨ are dual. The duality principle, also called De Morgan duality, asserts that Boolean algebra is unchanged when all dual pairs are interchanged.
One change not needed to make as part of this interchange was to complement. Complement is a self-dual operation. The identity or do-nothing operation x (copy the input to the output) is also self-dual. A more complicated example of a self-dual operation is (x ∧ y) ∨ (y ∧ z) ∨ (z ∧ x). There is no self-dual binary operation that depends on both its arguments. A composition of self-dual operations is a self-dual operation. For example, if f(x, y, z) = (x ∧ y) ∨ (y ∧ z) ∨ (z ∧ x), then f(f(x, y, z), x, t) is a self-dual operation of four arguments x, y, z, t.
The principle of duality can be explained from a group theory perspective by the fact that there are exactly four functions that are one-to-one mappings (automorphisms) of the set of Boolean polynomials back to itself: the identity function, the complement function, the dual function and the contradual function (complemented dual). These four functions form a group under function composition, isomorphic to the Klein four-group, acting on the set of Boolean polynomials. Walter Gottschalk remarked that consequently a more appropriate name for the phenomenon would be the principle (or square) of quaternality.[5]: 21–22
Diagrammatic representations
[edit]Venn diagrams
[edit]A Venn diagram[29] can be used as a representation of a Boolean operation using shaded overlapping regions. There is one region for each variable, all circular in the examples here. The interior and exterior of region x corresponds respectively to the values 1 (true) and 0 (false) for variable x. The shading indicates the value of the operation for each combination of regions, with dark denoting 1 and light 0 (some authors use the opposite convention).
The three Venn diagrams in the figure below represent respectively conjunction x ∧ y, disjunction x ∨ y, and complement ¬x.
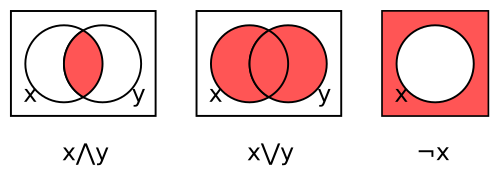
For conjunction, the region inside both circles is shaded to indicate that x ∧ y is 1 when both variables are 1. The other regions are left unshaded to indicate that x ∧ y is 0 for the other three combinations.
The second diagram represents disjunction x ∨ y by shading those regions that lie inside either or both circles. The third diagram represents complement ¬x by shading the region not inside the circle.
While we have not shown the Venn diagrams for the constants 0 and 1, they are trivial, being respectively a white box and a dark box, neither one containing a circle. However, we could put a circle for x in those boxes, in which case each would denote a function of one argument, x, which returns the same value independently of x, called a constant function. As far as their outputs are concerned, constants and constant functions are indistinguishable; the difference is that a constant takes no arguments, called a zeroary or nullary operation, while a constant function takes one argument, which it ignores, and is a unary operation.
Venn diagrams are helpful in visualizing laws. The commutativity laws for ∧ and ∨ can be seen from the symmetry of the diagrams: a binary operation that was not commutative would not have a symmetric diagram because interchanging x and y would have the effect of reflecting the diagram horizontally and any failure of commutativity would then appear as a failure of symmetry.
Idempotence of ∧ and ∨ can be visualized by sliding the two circles together and noting that the shaded area then becomes the whole circle, for both ∧ and ∨.
To see the first absorption law, x ∧ (x ∨ y) = x, start with the diagram in the middle for x ∨ y and note that the portion of the shaded area in common with the x circle is the whole of the x circle. For the second absorption law, x ∨ (x ∧ y) = x, start with the left diagram for x∧y and note that shading the whole of the x circle results in just the x circle being shaded, since the previous shading was inside the x circle.
The double negation law can be seen by complementing the shading in the third diagram for ¬x, which shades the x circle.
To visualize the first De Morgan's law, (¬x) ∧ (¬y) = ¬(x ∨ y), start with the middle diagram for x ∨ y and complement its shading so that only the region outside both circles is shaded, which is what the right hand side of the law describes. The result is the same as if we shaded that region which is both outside the x circle and outside the y circle, i.e. the conjunction of their exteriors, which is what the left hand side of the law describes.
The second De Morgan's law, (¬x) ∨ (¬y) = ¬(x ∧ y), works the same way with the two diagrams interchanged.
The first complement law, x ∧ ¬x = 0, says that the interior and exterior of the x circle have no overlap. The second complement law, x ∨ ¬x = 1, says that everything is either inside or outside the x circle.
Digital logic gates
[edit]Digital logic is the application of the Boolean algebra of 0 and 1 to electronic hardware consisting of logic gates connected to form a circuit diagram. Each gate implements a Boolean operation, and is depicted schematically by a shape indicating the operation. The shapes associated with the gates for conjunction (AND-gates), disjunction (OR-gates), and complement (inverters) are as follows:[30]

The lines on the left of each gate represent input wires or ports. The value of the input is represented by a voltage on the lead. For so-called "active-high" logic, 0 is represented by a voltage close to zero or "ground," while 1 is represented by a voltage close to the supply voltage; active-low reverses this. The line on the right of each gate represents the output port, which normally follows the same voltage conventions as the input ports.
Complement is implemented with an inverter gate. The triangle denotes the operation that simply copies the input to the output; the small circle on the output denotes the actual inversion complementing the input. The convention of putting such a circle on any port means that the signal passing through this port is complemented on the way through, whether it is an input or output port.
The duality principle, or De Morgan's laws, can be understood as asserting that complementing all three ports of an AND gate converts it to an OR gate and vice versa, as shown in Figure 4 below. Complementing both ports of an inverter however leaves the operation unchanged.

More generally, one may complement any of the eight subsets of the three ports of either an AND or OR gate. The resulting sixteen possibilities give rise to only eight Boolean operations, namely those with an odd number of 1s in their truth table. There are eight such because the "odd-bit-out" can be either 0 or 1 and can go in any of four positions in the truth table. There being sixteen binary Boolean operations, this must leave eight operations with an even number of 1s in their truth tables. Two of these are the constants 0 and 1 (as binary operations that ignore both their inputs); four are the operations that depend nontrivially on exactly one of their two inputs, namely x, y, ¬x, and ¬y; and the remaining two are x ⊕ y (XOR) and its complement x ≡ y.
Boolean algebras
[edit]The term "algebra" denotes both a subject, namely the subject of algebra, and an object, namely an algebraic structure. Whereas the foregoing has addressed the subject of Boolean algebra, this section deals with mathematical objects called Boolean algebras, defined in full generality as any model of the Boolean laws. We begin with a special case of the notion definable without reference to the laws, namely concrete Boolean algebras, and then give the formal definition of the general notion.
Concrete Boolean algebras
[edit]A concrete Boolean algebra or field of sets is any nonempty set of subsets of a given set X closed under the set operations of union, intersection, and complement relative to X.[5]
(Historically X itself was required to be nonempty as well to exclude the degenerate or one-element Boolean algebra, which is the one exception to the rule that all Boolean algebras satisfy the same equations since the degenerate algebra satisfies every equation. However, this exclusion conflicts with the preferred purely equational definition of "Boolean algebra", there being no way to rule out the one-element algebra using only equations— 0 ≠ 1 does not count, being a negated equation. Hence modern authors allow the degenerate Boolean algebra and let X be empty.)
Example 1. The power set 2X of X, consisting of all subsets of X. Here X may be any set: empty, finite, infinite, or even uncountable.
Example 2. The empty set and X. This two-element algebra shows that a concrete Boolean algebra can be finite even when it consists of subsets of an infinite set. It can be seen that every field of subsets of X must contain the empty set and X. Hence no smaller example is possible, other than the degenerate algebra obtained by taking X to be empty so as to make the empty set and X coincide.
Example 3. The set of finite and cofinite sets of integers, where a cofinite set is one omitting only finitely many integers. This is clearly closed under complement, and is closed under union because the union of a cofinite set with any set is cofinite, while the union of two finite sets is finite. Intersection behaves like union with "finite" and "cofinite" interchanged. This example is countably infinite because there are only countably many finite sets of integers.
Example 4. For a less trivial example of the point made by example 2, consider a Venn diagram formed by n closed curves partitioning the diagram into 2n regions, and let X be the (infinite) set of all points in the plane not on any curve but somewhere within the diagram. The interior of each region is thus an infinite subset of X, and every point in X is in exactly one region. Then the set of all 22n possible unions of regions (including the empty set obtained as the union of the empty set of regions and X obtained as the union of all 2n regions) is closed under union, intersection, and complement relative to X and therefore forms a concrete Boolean algebra. Again, there are finitely many subsets of an infinite set forming a concrete Boolean algebra, with example 2 arising as the case n = 0 of no curves.
Subsets as bit vectors
[edit]A subset Y of X can be identified with an indexed family of bits with index set X, with the bit indexed by x ∈ X being 1 or 0 according to whether or not x ∈ Y. (This is the so-called characteristic function notion of a subset.) For example, a 32-bit computer word consists of 32 bits indexed by the set {0,1,2,...,31}, with 0 and 31 indexing the low and high order bits respectively. For a smaller example, if where a, b, c are viewed as bit positions in that order from left to right, the eight subsets {}, {c}, {b}, {b,c}, {a}, {a,c}, {a,b}, and {a,b,c} of X can be identified with the respective bit vectors 000, 001, 010, 011, 100, 101, 110, and 111. Bit vectors indexed by the set of natural numbers are infinite sequences of bits, while those indexed by the reals in the unit interval [0,1] are packed too densely to be able to write conventionally but nonetheless form well-defined indexed families (imagine coloring every point of the interval [0,1] either black or white independently; the black points then form an arbitrary subset of [0,1]).
From this bit vector viewpoint, a concrete Boolean algebra can be defined equivalently as a nonempty set of bit vectors all of the same length (more generally, indexed by the same set) and closed under the bit vector operations of bitwise ∧, ∨, and ¬, as in 1010∧0110 = 0010, 1010∨0110 = 1110, and ¬1010 = 0101, the bit vector realizations of intersection, union, and complement respectively.
Prototypical Boolean algebra
[edit]The set {0,1} and its Boolean operations as treated above can be understood as the special case of bit vectors of length one, which by the identification of bit vectors with subsets can also be understood as the two subsets of a one-element set. This is called the prototypical Boolean algebra, justified by the following observation.
- The laws satisfied by all nondegenerate concrete Boolean algebras coincide with those satisfied by the prototypical Boolean algebra.
This observation is proved as follows. Certainly any law satisfied by all concrete Boolean algebras is satisfied by the prototypical one since it is concrete. Conversely any law that fails for some concrete Boolean algebra must have failed at a particular bit position, in which case that position by itself furnishes a one-bit counterexample to that law. Nondegeneracy ensures the existence of at least one bit position because there is only one empty bit vector.
The final goal of the next section can be understood as eliminating "concrete" from the above observation. That goal is reached via the stronger observation that, up to isomorphism, all Boolean algebras are concrete.
Boolean algebras: the definition
[edit]The Boolean algebras so far have all been concrete, consisting of bit vectors or equivalently of subsets of some set. Such a Boolean algebra consists of a set and operations on that set which can be shown to satisfy the laws of Boolean algebra.
Instead of showing that the Boolean laws are satisfied, we can instead postulate a set X, two binary operations on X, and one unary operation, and require that those operations satisfy the laws of Boolean algebra. The elements of X need not be bit vectors or subsets but can be anything at all. This leads to the more general abstract definition.
- A Boolean algebra is any set with binary operations ∧ and ∨ and a unary operation ¬ thereon satisfying the Boolean laws.[31]
For the purposes of this definition it is irrelevant how the operations came to satisfy the laws, whether by fiat or proof. All concrete Boolean algebras satisfy the laws (by proof rather than fiat), whence every concrete Boolean algebra is a Boolean algebra according to our definitions. This axiomatic definition of a Boolean algebra as a set and certain operations satisfying certain laws or axioms by fiat is entirely analogous to the abstract definitions of group, ring, field etc. characteristic of modern or abstract algebra.
Given any complete axiomatization of Boolean algebra, such as the axioms for a complemented distributive lattice, a sufficient condition for an algebraic structure of this kind to satisfy all the Boolean laws is that it satisfy just those axioms. The following is therefore an equivalent definition.
- A Boolean algebra is a complemented distributive lattice.
The section on axiomatization lists other axiomatizations, any of which can be made the basis of an equivalent definition.
Representable Boolean algebras
[edit]Although every concrete Boolean algebra is a Boolean algebra, not every Boolean algebra need be concrete. Let n be a square-free positive integer, one not divisible by the square of an integer, for example 30 but not 12. The operations of greatest common divisor, least common multiple, and division into n (that is, ¬x = n/x), can be shown to satisfy all the Boolean laws when their arguments range over the positive divisors of n. Hence those divisors form a Boolean algebra. These divisors are not subsets of a set, making the divisors of n a Boolean algebra that is not concrete according to our definitions.
However, if each divisor of n is represented by the set of its prime factors, this nonconcrete Boolean algebra is isomorphic to the concrete Boolean algebra consisting of all sets of prime factors of n, with union corresponding to least common multiple, intersection to greatest common divisor, and complement to division into n. So this example, while not technically concrete, is at least "morally" concrete via this representation, called an isomorphism. This example is an instance of the following notion.
- A Boolean algebra is called representable when it is isomorphic to a concrete Boolean algebra.
The next question is answered positively as follows.
- Every Boolean algebra is representable.
That is, up to isomorphism, abstract and concrete Boolean algebras are the same thing. This result depends on the Boolean prime ideal theorem, a choice principle slightly weaker than the axiom of choice. This strong relationship implies a weaker result strengthening the observation in the previous subsection to the following easy consequence of representability.
- The laws satisfied by all Boolean algebras coincide with those satisfied by the prototypical Boolean algebra.
It is weaker in the sense that it does not of itself imply representability. Boolean algebras are special here, for example a relation algebra is a Boolean algebra with additional structure but it is not the case that every relation algebra is representable in the sense appropriate to relation algebras.
Axiomatizing Boolean algebra
[edit]The above definition of an abstract Boolean algebra as a set together with operations satisfying "the" Boolean laws raises the question of what those laws are. A simplistic answer is "all Boolean laws", which can be defined as all equations that hold for the Boolean algebra of 0 and 1. However, since there are infinitely many such laws, this is not a satisfactory answer in practice, leading to the question of it suffices to require only finitely many laws to hold.
In the case of Boolean algebras, the answer is "yes": the finitely many equations listed above are sufficient. Thus, Boolean algebra is said to be finitely axiomatizable or finitely based.
Moreover, the number of equations needed can be further reduced. To begin with, some of the above laws are implied by some of the others. A sufficient subset of the above laws consists of the pairs of associativity, commutativity, and absorption laws, distributivity of ∧ over ∨ (or the other distributivity law—one suffices), and the two complement laws. In fact, this is the traditional axiomatization of Boolean algebra as a complemented distributive lattice.
By introducing additional laws not listed above, it becomes possible to shorten the list of needed equations yet further; for instance, with the vertical bar representing the Sheffer stroke operation, the single axiom is sufficient to completely axiomatize Boolean algebra. It is also possible to find longer single axioms using more conventional operations; see Minimal axioms for Boolean algebra.[32]
Propositional logic
[edit]Propositional logic is a logical system that is intimately connected to Boolean algebra.[5] Many syntactic concepts of Boolean algebra carry over to propositional logic with only minor changes in notation and terminology, while the semantics of propositional logic are defined via Boolean algebras in a way that the tautologies (theorems) of propositional logic correspond to equational theorems of Boolean algebra.
Syntactically, every Boolean term corresponds to a propositional formula of propositional logic. In this translation between Boolean algebra and propositional logic, Boolean variables x, y, ... become propositional variables (or atoms) P, Q, ... Boolean terms such as x ∨ y become propositional formulas P ∨ Q; 0 becomes false or ⊥, and 1 becomes true or ⊤. It is convenient when referring to generic propositions to use Greek letters Φ, Ψ, ... as metavariables (variables outside the language of propositional calculus, used when talking about propositional calculus) to denote propositions.
The semantics of propositional logic rely on truth assignments. The essential idea of a truth assignment is that the propositional variables are mapped to elements of a fixed Boolean algebra, and then the truth value of a propositional formula using these letters is the element of the Boolean algebra that is obtained by computing the value of the Boolean term corresponding to the formula. In classical semantics, only the two-element Boolean algebra is used, while in Boolean-valued semantics arbitrary Boolean algebras are considered. A tautology is a propositional formula that is assigned truth value 1 by every truth assignment of its propositional variables to an arbitrary Boolean algebra (or, equivalently, every truth assignment to the two element Boolean algebra).
These semantics permit a translation between tautologies of propositional logic and equational theorems of Boolean algebra. Every tautology Φ of propositional logic can be expressed as the Boolean equation Φ = 1, which will be a theorem of Boolean algebra. Conversely, every theorem Φ = Ψ of Boolean algebra corresponds to the tautologies (Φ ∨ ¬Ψ) ∧ (¬Φ ∨ Ψ) and (Φ ∧ Ψ) ∨ (¬Φ ∧ ¬Ψ). If → is in the language, these last tautologies can also be written as (Φ → Ψ) ∧ (Ψ → Φ), or as two separate theorems Φ → Ψ and Ψ → Φ; if ≡ is available, then the single tautology Φ ≡ Ψ can be used.
Applications
[edit]One motivating application of propositional calculus is the analysis of propositions and deductive arguments in natural language.[33] Whereas the proposition "if x = 3, then x + 1 = 4" depends on the meanings of such symbols as + and 1, the proposition "if x = 3, then x = 3" does not; it is true merely by virtue of its structure, and remains true whether "x = 3" is replaced by "x = 4" or "the moon is made of green cheese." The generic or abstract form of this tautology is "if P, then P," or in the language of Boolean algebra, P → P.[citation needed]
Replacing P by x = 3 or any other proposition is called instantiation of P by that proposition. The result of instantiating P in an abstract proposition is called an instance of the proposition. Thus, x = 3 → x = 3 is a tautology by virtue of being an instance of the abstract tautology P → P. All occurrences of the instantiated variable must be instantiated with the same proposition, to avoid such nonsense as P → x = 3 or x = 3 → x = 4.
Propositional calculus restricts attention to abstract propositions, those built up from propositional variables using Boolean operations. Instantiation is still possible within propositional calculus, but only by instantiating propositional variables by abstract propositions, such as instantiating Q by Q → P in P → (Q → P) to yield the instance P → ((Q → P) → P).
(The availability of instantiation as part of the machinery of propositional calculus avoids the need for metavariables within the language of propositional calculus, since ordinary propositional variables can be considered within the language to denote arbitrary propositions. The metavariables themselves are outside the reach of instantiation, not being part of the language of propositional calculus but rather part of the same language for talking about it that this sentence is written in, where there is a need to be able to distinguish propositional variables and their instantiations as being distinct syntactic entities.)
Deductive systems for propositional logic
[edit]An axiomatization of propositional calculus is a set of tautologies called axioms and one or more inference rules for producing new tautologies from old. A proof in an axiom system A is a finite nonempty sequence of propositions each of which is either an instance of an axiom of A or follows by some rule of A from propositions appearing earlier in the proof (thereby disallowing circular reasoning). The last proposition is the theorem proved by the proof. Every nonempty initial segment of a proof is itself a proof, whence every proposition in a proof is itself a theorem. An axiomatization is sound when every theorem is a tautology, and complete when every tautology is a theorem.[34]
Sequent calculus
[edit]Propositional calculus is commonly organized as a Hilbert system, whose operations are just those of Boolean algebra and whose theorems are Boolean tautologies, those Boolean terms equal to the Boolean constant 1. Another form is sequent calculus, which has two sorts, propositions as in ordinary propositional calculus, and pairs of lists of propositions called sequents, such as A ∨ B, A ∧ C, ... ⊢ A, B → C, .... The two halves of a sequent are called the antecedent and the succedent respectively. The customary metavariable denoting an antecedent or part thereof is Γ, and for a succedent Δ; thus Γ, A ⊢ Δ would denote a sequent whose succedent is a list Δ and whose antecedent is a list Γ with an additional proposition A appended after it. The antecedent is interpreted as the conjunction of its propositions, the succedent as the disjunction of its propositions, and the sequent itself as the entailment of the succedent by the antecedent.
Entailment differs from implication in that whereas the latter is a binary operation that returns a value in a Boolean algebra, the former is a binary relation which either holds or does not hold. In this sense, entailment is an external form of implication, meaning external to the Boolean algebra, thinking of the reader of the sequent as also being external and interpreting and comparing antecedents and succedents in some Boolean algebra. The natural interpretation of ⊢ is as ≤ in the partial order of the Boolean algebra defined by x ≤ y just when x ∨ y = y. This ability to mix external implication ⊢ and internal implication → in the one logic is among the essential differences between sequent calculus and propositional calculus.[35]
Applications
[edit]Boolean algebra as the calculus of two values is fundamental to computer circuits, computer programming, and mathematical logic, and is also used in other areas of mathematics such as set theory and statistics.[5]
Computers
[edit]In the early 20th century, several electrical engineers[who?] intuitively recognized that Boolean algebra was analogous to the behavior of certain types of electrical circuits. Claude Shannon formally proved such behavior was logically equivalent to Boolean algebra in his 1937 master's thesis, A Symbolic Analysis of Relay and Switching Circuits.
Today, all modern general-purpose computers perform their functions using two-value Boolean logic; that is, their electrical circuits are a physical manifestation of two-value Boolean logic. They achieve this in various ways: as voltages on wires in high-speed circuits and capacitive storage devices, as orientations of a magnetic domain in ferromagnetic storage devices, as holes in punched cards or paper tape, and so on. (Some early computers used decimal circuits or mechanisms instead of two-valued logic circuits.)
Of course, it is possible to code more than two symbols in any given medium. For example, one might use respectively 0, 1, 2, and 3 volts to code a four-symbol alphabet on a wire, or holes of different sizes in a punched card. In practice, the tight constraints of high speed, small size, and low power combine to make noise a major factor. This makes it hard to distinguish between symbols when there are several possible symbols that could occur at a single site. Rather than attempting to distinguish between four voltages on one wire, digital designers have settled on two voltages per wire, high and low.
Computers use two-value Boolean circuits for the above reasons. The most common computer architectures use ordered sequences of Boolean values, called bits, of 32 or 64 values, e.g. 01101000110101100101010101001011. When programming in machine code, assembly language, and certain other programming languages, programmers work with the low-level digital structure of the data registers. These registers operate on voltages, where zero volts represents Boolean 0, and a reference voltage (often +5 V, +3.3 V, or +1.8 V) represents Boolean 1. Such languages support both numeric operations and logical operations. In this context, "numeric" means that the computer treats sequences of bits as binary numbers (base two numbers) and executes arithmetic operations like add, subtract, multiply, or divide. "Logical" refers to the Boolean logical operations of disjunction, conjunction, and negation between two sequences of bits, in which each bit in one sequence is simply compared to its counterpart in the other sequence. Programmers therefore have the option of working in and applying the rules of either numeric algebra or Boolean algebra as needed. A core differentiating feature between these families of operations is the existence of the carry operation in the first but not the second.
Two-valued logic
[edit]Other areas where two values is a good choice are the law and mathematics. In everyday relaxed conversation, nuanced or complex answers such as "maybe" or "only on the weekend" are acceptable. In more focused situations such as a court of law or theorem-based mathematics, however, it is deemed advantageous to frame questions so as to admit a simple yes-or-no answer—is the defendant guilty or not guilty, is the proposition true or false—and to disallow any other answer. However, limiting this might prove in practice for the respondent, the principle of the simple yes–no question has become a central feature of both judicial and mathematical logic, making two-valued logic deserving of organization and study in its own right.
A central concept of set theory is membership. An organization may permit multiple degrees of membership, such as novice, associate, and full. With sets, however, an element is either in or out. The candidates for membership in a set work just like the wires in a digital computer: each candidate is either a member or a nonmember, just as each wire is either high or low.
Algebra being a fundamental tool in any area amenable to mathematical treatment, these considerations combine to make the algebra of two values of fundamental importance to computer hardware, mathematical logic, and set theory.
Two-valued logic can be extended to multi-valued logic, notably by replacing the Boolean domain {0, 1} with the unit interval [0,1], in which case rather than only taking values 0 or 1, any value between and including 0 and 1 can be assumed. Algebraically, negation (NOT) is replaced with 1 − x, conjunction (AND) is replaced with multiplication (xy), and disjunction (OR) is defined via De Morgan's law. Interpreting these values as logical truth values yields a multi-valued logic, which forms the basis for fuzzy logic and probabilistic logic. In these interpretations, a value is interpreted as the "degree" of truth – to what extent a proposition is true, or the probability that the proposition is true.
Boolean operations
[edit]The original application for Boolean operations was mathematical logic, where it combines the truth values, true or false, of individual formulas.
Natural language
[edit]Natural languages such as English have words for several Boolean operations, in particular conjunction (and), disjunction (or), negation (not), and implication (implies). But not is synonymous with and not. When used to combine situational assertions such as "the block is on the table" and "cats drink milk", which naïvely are either true or false, the meanings of these logical connectives often have the meaning of their logical counterparts. However, with descriptions of behavior such as "Jim walked through the door", one starts to notice differences such as failure of commutativity, for example, the conjunction of "Jim opened the door" with "Jim walked through the door" in that order is not equivalent to their conjunction in the other order, since and usually means and then in such cases. Questions can be similar: the order "Is the sky blue, and why is the sky blue?" makes more sense than the reverse order. Conjunctive commands about behavior are like behavioral assertions, as in get dressed and go to school. Disjunctive commands such love me or leave me or fish or cut bait tend to be asymmetric via the implication that one alternative is less preferable. Conjoined nouns such as tea and milk generally describe aggregation as with set union while tea or milk is a choice. However, context can reverse these senses, as in your choices are coffee and tea which usually means the same as your choices are coffee or tea (alternatives). Double negation, as in "I don't not like milk", rarely means literally "I do like milk" but rather conveys some sort of hedging, as though to imply that there is a third possibility. "Not not P" can be loosely interpreted as "surely P", and although P necessarily implies "not not P," the converse is suspect in English, much as with intuitionistic logic. In view of the highly idiosyncratic usage of conjunctions in natural languages, Boolean algebra cannot be considered a reliable framework for interpreting them.
Digital logic
[edit]Boolean operations are used in digital logic to combine the bits carried on individual wires, thereby interpreting them over {0,1}. When a vector of n identical binary gates are used to combine two bit vectors each of n bits, the individual bit operations can be understood collectively as a single operation on values from a Boolean algebra with 2n elements.
Naive set theory
[edit]Naive set theory interprets Boolean operations as acting on subsets of a given set X. As we saw earlier this behavior exactly parallels the coordinate-wise combinations of bit vectors, with the union of two sets corresponding to the disjunction of two bit vectors and so on.
Video cards
[edit]The 256-element free Boolean algebra on three generators is deployed in computer displays based on raster graphics, which use bit blit to manipulate whole regions consisting of pixels, relying on Boolean operations to specify how the source region should be combined with the destination, typically with the help of a third region called the mask. Modern video cards offer all 223 = 256 ternary operations for this purpose, with the choice of operation being a one-byte (8-bit) parameter. The constants SRC = 0xaa or 0b10101010, DST = 0xcc or 0b11001100, and MSK = 0xf0 or 0b11110000 allow Boolean operations such as (SRC^DST)&MSK (meaning XOR the source and destination and then AND the result with the mask) to be written directly as a constant denoting a byte calculated at compile time, 0x80 in the (SRC^DST)&MSK example, 0x88 if just SRC^DST, etc. At run time the video card interprets the byte as the raster operation indicated by the original expression in a uniform way that requires remarkably little hardware and which takes time completely independent of the complexity of the expression.
Modeling and CAD
[edit]Solid modeling systems for computer aided design offer a variety of methods for building objects from other objects, combination by Boolean operations being one of them. In this method the space in which objects exist is understood as a set S of voxels (the three-dimensional analogue of pixels in two-dimensional graphics) and shapes are defined as subsets of S, allowing objects to be combined as sets via union, intersection, etc. One obvious use is in building a complex shape from simple shapes simply as the union of the latter. Another use is in sculpting understood as removal of material: any grinding, milling, routing, or drilling operation that can be performed with physical machinery on physical materials can be simulated on the computer with the Boolean operation x ∧ ¬y or x − y, which in set theory is set difference, remove the elements of y from those of x. Thus given two shapes one to be machined and the other the material to be removed, the result of machining the former to remove the latter is described simply as their set difference.
Boolean searches
[edit]Search engine queries also employ Boolean logic. For this application, each web page on the Internet may be considered to be an "element" of a "set." The following examples use a syntax supported by Google.[NB 1]
- Doublequotes are used to combine whitespace-separated words into a single search term.[NB 2]
- Whitespace is used to specify logical AND, as it is the default operator for joining search terms:
"Search term 1" "Search term 2"
- The OR keyword is used for logical OR:
"Search term 1" OR "Search term 2"
- A prefixed minus sign is used for logical NOT:
"Search term 1" −"Search term 2"
See also
[edit]Notes
[edit]- ^ Not all search engines support the same query syntax. Additionally, some organizations (such as Google) provide "specialized" search engines that support alternate or extended syntax. (See, Syntax cheatsheet.) The now-defunct Google code search used to support regular expressions but no longer exists.
- ^ Doublequote-delimited search terms are called "exact phrase" searches in the Google documentation.
References
[edit]- ^ Boole, George (2011-07-28). The Mathematical Analysis of Logic - Being an Essay Towards a Calculus of Deductive Reasoning.
- ^ Boole, George (2003) [1854]. An Investigation of the Laws of Thought. Prometheus Books. ISBN 978-1-59102-089-9.
- ^ "The name Boolean algebra (or Boolean 'algebras') for the calculus originated by Boole, extended by Schröder, and perfected by Whitehead seems to have been first suggested by Sheffer, in 1913." Edward Vermilye Huntington, "New sets of independent postulates for the algebra of logic, with special reference to Whitehead and Russell's Principia mathematica", in Transactions of the American Mathematical Society 35 (1933), 274-304; footnote, page 278.
- ^ Peirce, Charles S. (1931). Collected Papers. Vol. 3. Harvard University Press. p. 13. ISBN 978-0-674-13801-8.
{{cite book}}: ISBN / Date incompatibility (help) - ^ a b c d e f g Givant, Steven R.; Halmos, Paul Richard (2009). Introduction to Boolean Algebras. Undergraduate Texts in Mathematics, Springer. pp. 21–22. ISBN 978-0-387-40293-2.
- ^ Nelson, Eric S. (2011). "The Yijing and Philosophy: From Leibniz to Derrida". Journal of Chinese Philosophy. 38 (3): 377–396. doi:10.1111/j.1540-6253.2011.01661.x.
- ^ Lenzen, Wolfgang. "Leibniz: Logic". In Fieser, James; Dowden, Bradley (eds.). Internet Encyclopedia of Philosophy. ISSN 2161-0002. OCLC 37741658.
- ^ a b c Dunn, J. Michael; Hardegree, Gary M. (2001). Algebraic methods in philosophical logic. Oxford University Press. p. 2. ISBN 978-0-19-853192-0.
- ^ Bimbó, Katalin; Dunn, J. Michael (2008). Generalized Galois Logics: Relational Semantics of Nonclassical Logical Calculi. CSLI Publications. ISBN 978-1-57586-573-7.
- ^ Stone, M. H. (1936). "The Theory of Representation for Boolean Algebras". Transactions of the American Mathematical Society. 40 (1): 37–111. doi:10.2307/1989664. ISSN 0002-9947. JSTOR 1989664.
- ^ Weisstein, Eric W. "Boolean Algebra". mathworld.wolfram.com. Retrieved 2020-09-02.
- ^ Balabanian, Norman; Carlson, Bradley (2001). Digital logic design principles. John Wiley. pp. 39–40. ISBN 978-0-471-29351-4., online sample
- ^ Rajaraman; Radhakrishnan (2008-03-01). Introduction To Digital Computer Design. PHI Learning Pvt. Ltd. p. 65. ISBN 978-81-203-3409-0.
- ^ Camara, John A. (2010). Electrical and Electronics Reference Manual for the Electrical and Computer PE Exam. www.ppi2pass.com. p. 41. ISBN 978-1-59126-166-7.
- ^ Shin-ichi Minato, Saburo Muroga (2007). "Chapter 29: Binary Decision Diagrams". In Chen, Wai-Kai (ed.). The VLSI handbook (2 ed.). CRC Press. ISBN 978-0-8493-4199-1.
- ^ Parkes, Alan (2002). Introduction to languages, machines and logic: computable languages, abstract machines and formal logic. Springer. p. 276. ISBN 978-1-85233-464-2.
- ^ Barwise, Jon; Etchemendy, John; Allwein, Gerard; Barker-Plummer, Dave; Liu, Albert (1999). Language, proof, and logic. CSLI Publications. ISBN 978-1-889119-08-3.
- ^ Goertzel, Ben (1994). Chaotic logic: language, thought, and reality from the perspective of complex systems science. Springer. p. 48. ISBN 978-0-306-44690-0.
- ^ Halmos, Paul Richard (1963). Lectures on Boolean Algebras. van Nostrand.
- ^ Bacon, Jason W. (2011). "Computer Science 315 Lecture Notes". Archived from the original on 2021-10-02. Retrieved 2021-10-01.
- ^ "Boolean Algebra - Expression, Rules, Theorems, and Examples". GeeksforGeeks. 2021-09-24. Retrieved 2024-06-03.
- ^ "Boolean Logical Operations" (PDF).
- ^ "Boolean Algebra Operations". bob.cs.sonoma.edu. Retrieved 2024-06-03.
- ^ "Boolean Algebra" (PDF).
- ^ O'Regan, Gerard (2008). A brief history of computing. Springer. p. 33. ISBN 978-1-84800-083-4.
- ^ "Elements of Boolean Algebra". www.ee.surrey.ac.uk. Archived from the original on 2020-07-21. Retrieved 2020-09-02.
- ^ McGee, Vann, Sentential Calculus Revisited: Boolean Algebra (PDF)
- ^ Goodstein, Reuben Louis (2012), "Chapter 4: Sentence Logic", Boolean Algebra, Courier Dover Publications, ISBN 978-0-48615497-8
- ^ Venn, John (July 1880). "I. On the Diagrammatic and Mechanical Representation of Propositions and Reasonings" (PDF). The London, Edinburgh, and Dublin Philosophical Magazine and Journal of Science. 5. 10 (59): 1–18. doi:10.1080/14786448008626877. Archived (PDF) from the original on 2017-05-16. [1] [2]
- ^ Shannon, Claude (1949). "The Synthesis of Two-Terminal Switching Circuits". Bell System Technical Journal. 28: 59–98. Bibcode:1949BSTJ...28...59S. doi:10.1002/j.1538-7305.1949.tb03624.x.
- ^ Koppelberg, Sabine (1989). "General Theory of Boolean Algebras". Handbook of Boolean Algebras, Vol. 1 (ed. J. Donald Monk with Robert Bonnet). Amsterdam, Netherlands: North Holland. ISBN 978-0-444-70261-6.
- ^ McCune, William; Veroff, Robert; Fitelson, Branden; Harris, Kenneth; Feist, Andrew; Wos, Larry (2002), "Short single axioms for Boolean algebra", Journal of Automated Reasoning, 29 (1): 1–16, doi:10.1023/A:1020542009983, MR 1940227, S2CID 207582048
- ^ Allwood, Jens; Andersson, Gunnar-Gunnar; Andersson, Lars-Gunnar; Dahl, Osten (1977-09-15). Logic in Linguistics. Cambridge University Press. ISBN 978-0-521-29174-3.
- ^ Hausman, Alan; Kahane, Howard; Tidman, Paul (2010) [2007]. Logic and Philosophy: A Modern Introduction. Wadsworth Cengage Learning. ISBN 978-0-495-60158-6.
- ^ Girard, Jean-Yves; Taylor, Paul; Lafont, Yves (1990) [1989]. Proofs and Types. Cambridge University Press (Cambridge Tracts in Theoretical Computer Science, 7). ISBN 978-0-521-37181-0.
Further reading
[edit]- Mano, Morris; Ciletti, Michael D. (2013). Digital Design. Pearson. ISBN 978-0-13-277420-8.
- Whitesitt, J. Eldon (1995). Boolean algebra and its applications. Courier Dover Publications. ISBN 978-0-486-68483-3.
- Dwinger, Philip (1971). Introduction to Boolean algebras. Würzburg, Germany: Physica Verlag.
- Sikorski, Roman (1969). Boolean Algebras (3 ed.). Berlin, Germany: Springer-Verlag. ISBN 978-0-387-04469-9.
- Bocheński, Józef Maria (1959). A Précis of Mathematical Logic. Translated from the French and German editions by Otto Bird. Dordrecht, South Holland: D. Reidel.
Historical perspective
[edit]- Boole, George (1848). "The Calculus of Logic". Cambridge and Dublin Mathematical Journal. III: 183–198.
- Hailperin, Theodore (1986). Boole's logic and probability: a critical exposition from the standpoint of contemporary algebra, logic, and probability theory (2 ed.). Elsevier. ISBN 978-0-444-87952-3.
- Gabbay, Dov M.; Woods, John, eds. (2004). The rise of modern logic: from Leibniz to Frege. Handbook of the History of Logic. Vol. 3. Elsevier. ISBN 978-0-444-51611-4., several relevant chapters by Hailperin, Valencia, and Grattan-Guinness
- Badesa, Calixto (2004). "Chapter 1. Algebra of Classes and Propositional Calculus". The birth of model theory: Löwenheim's theorem in the frame of the theory of relatives. Princeton University Press. ISBN 978-0-691-05853-5.
- Stanković, Radomir S. [in German]; Astola, Jaakko Tapio [in Finnish] (2011). Written at Niš, Serbia & Tampere, Finland. From Boolean Logic to Switching Circuits and Automata: Towards Modern Information Technology. Studies in Computational Intelligence. Vol. 335 (1 ed.). Berlin & Heidelberg, Germany: Springer-Verlag. pp. xviii + 212. doi:10.1007/978-3-642-11682-7. ISBN 978-3-642-11681-0. ISSN 1860-949X. LCCN 2011921126. Retrieved 2022-10-25.
- "The Algebra of Logic Tradition" entry by Burris, Stanley in the Stanford Encyclopedia of Philosophy, 21 February 2012
External links
[edit]Boolean algebra
View on GrokipediaFundamentals
Truth Values
Boolean algebra operates over a domain consisting of exactly two distinct elements, commonly denoted as 0 and 1, or equivalently as false and true.[10] These elements represent the fundamental truth values in the system: 0 signifies falsity or the absence of a property, while 1 denotes truth or the presence of a property.[10] In applied contexts, such as digital electronics, 0 and 1 further correspond to off and on states, respectively, enabling binary representation in computational systems.[11] The use of 1 and 0 as symbolic representatives for logical quantities originated with George Boole in his seminal work The Mathematical Analysis of Logic (1847), where 1 denoted the universal class (encompassing all objects) and 0 represented the empty class (no objects).[12] Boole employed these symbols to formalize deductive reasoning, treating propositions as equations that equate to 1 for true statements and 0 for false ones, laying the groundwork for algebraic treatment of logic.[12] This notation proved instrumental in bridging arithmetic operations with logical inference.[11] At its core, Boolean algebra embodies two-valued or bivalent logic, meaning every proposition must assume precisely one of the two truth values without intermediate possibilities.[10] This bivalence stems from the classical principle that propositions are either true or false, excluding gradations or uncertainties, which distinguishes it from multi-valued logics.[13] The strict duality ensures a complete and decidable framework for logical evaluation.[10] For instance, consider the simple declarative statement "It is raining." In Boolean algebra, this statement is assigned either the truth value true (1) if rain is occurring, or false (0) if it is not, with no allowance for partial truth such as "somewhat raining."[10] This assignment exemplifies how Boolean truth values model binary propositions in everyday reasoning and formal systems alike.[13]Basic Operations
Boolean algebra features three primary operations for manipulating truth values: conjunction (AND, denoted ∧), disjunction (OR, denoted ∨), and negation (NOT, denoted ¬). These operations, originally formalized by George Boole using algebraic symbols for logical combination, form the foundation for expressing complex logical relationships from the basic truth values of false (0) and true (1).[14] Conjunction and disjunction are binary operations that combine two inputs, while negation is unary, applying to a single input.[15] The conjunction operation, AND (∧), yields true (1) if and only if both inputs are true (1); otherwise, it yields false (0). Symbolically, for truth values a and b, a ∧ b = 1 if and only if both a = 1 and b = 1.[16] Intuitively, it represents the notion of "both" conditions holding simultaneously, such as both events occurring or both switches being closed in a series electrical circuit.[17] Its truth table is as follows:| a | b | a ∧ b |
|---|---|---|
| 0 | 0 | 0 |
| 0 | 1 | 0 |
| 1 | 0 | 0 |
| 1 | 1 | 1 |
| a | b | a ∨ b |
|---|---|---|
| 0 | 0 | 0 |
| 0 | 1 | 1 |
| 1 | 0 | 1 |
| 1 | 1 | 1 |
| a | ¬a |
|---|---|
| 0 | 1 |
| 1 | 0 |
Derived Operations
In Boolean algebra, derived operations are constructed by composing the basic operations of conjunction (∧), disjunction (∨), and negation (¬), enabling the expression of more complex logical relationships while maintaining the two-valued truth system. These operations facilitate simplification of Boolean expressions and find applications in circuit design and formal reasoning.[19] Material implication, denoted as → or ⊃, represents the conditional "if a then b" and is false only when a is true and b is false; otherwise, it is true. This corresponds to the formula . Its truth table is:| a | b | a → b |
|---|---|---|
| 0 | 0 | 1 |
| 0 | 1 | 1 |
| 1 | 0 | 0 |
| 1 | 1 | 1 |
| a | b | a ↔ b |
|---|---|---|
| 0 | 0 | 1 |
| 0 | 1 | 0 |
| 1 | 0 | 0 |
| 1 | 1 | 1 |
| a | b | a ⊕ b |
|---|---|---|
| 0 | 0 | 0 |
| 0 | 1 | 1 |
| 1 | 0 | 1 |
| 1 | 1 | 0 |
| a | b | a NAND b |
|---|---|---|
| 0 | 0 | 1 |
| 0 | 1 | 1 |
| 1 | 0 | 1 |
| 1 | 1 | 0 |
| a | b | a NOR b |
|---|---|---|
| 0 | 0 | 1 |
| 0 | 1 | 0 |
| 1 | 0 | 0 |
| 1 | 1 | 0 |
Properties and Laws
Core Laws
The core laws of Boolean algebra constitute the foundational identities governing the operations of conjunction (∧, AND), disjunction (∨, OR), and negation (¬, NOT), enabling systematic simplification and equivalence proofs for Boolean expressions. These laws, analogous to those in arithmetic, ensure that Boolean algebra behaves as a consistent algebraic structure. They form the basis for deriving more complex properties and were systematically axiomatized by Edward V. Huntington in his 1904 paper, where commutative, associative (derived), distributive, and idempotent (derived) laws are central to the postulates.[22] The commutative laws state that the order of operands does not affect the result for both conjunction and disjunction: These hold for any Boolean elements and , allowing rearrangement in expressions without altering meaning, as established in Huntington's postulates IIIa and IIIb.[22] The associative laws permit grouping of operands in sequences of the same operation: Derived as theorems from Huntington's axioms, these laws eliminate the need for parentheses in chains of ∧ or ∨ operations.[22] The identity laws involve the constant elements 0 (false) and 1 (true), where ∧ with 1 and ∨ with 0 leave an expression unchanged: These reflect the neutral roles of 1 in conjunction and 0 in disjunction, directly from Huntington's postulates IIa and IIb (adjusted for notation).[22] The complement laws demonstrate how negation interacts with the other operations to produce constants: For any , these laws capture the exhaustive and exclusive nature of an element and its complement, formalized in Huntington's postulate V.[22] The distributive laws show how one operation spreads over the other, mirroring arithmetic distribution: These are core postulates IVa and IVb in Huntington's system, crucial for factoring and expanding expressions.[22] The idempotent laws indicate that repeating an operand yields the operand itself: Derived from the axioms (theorems VIIIa and VIIIb in Huntington), these simplify redundant terms, such as reducing to .[22] These laws facilitate practical simplifications; for instance, applying the distributive and complement laws to yields via idempotence and identity, demonstrating how expressions can be reduced to minimal forms.[22]Monotonic and Absorption Laws
In Boolean algebra, a partial order ≤ is defined on the elements such that for any elements and , if and only if . This relation is reflexive, antisymmetric, and transitive, making the algebra a partially ordered set (poset) with least element 0 and greatest element 1. Equivalently, holds if , reflecting the implication in logical terms.[23][24] The monotonicity laws arise from this partial order and ensure that the operations preserve the ordering. Specifically, if , then for any element , it follows that and . These properties indicate that conjunction and disjunction are monotone functions with respect to the order, meaning that increasing one operand (while keeping the other fixed) cannot decrease the result. To verify when , note that since , distributivity yields , so the order holds. A similar argument applies to disjunction using the dual property./19:_Lattices_and_Boolean_Algebras/19.02:_Boolean_Algebras The absorption laws provide identities for eliminating redundant terms: and . These can be derived from the monotonicity and other core properties; for instance, by distributivity, and then by idempotence and the order, it simplifies to . The laws highlight how one operation "absorbs" the effect of the other when combined with the same element.[25] These laws are essential for simplifying Boolean expressions by removing redundancies. For example, in the expression , absorption yields , as the disjunction term is absorbed, reducing complexity without altering the function. Similarly, simplifies to , eliminating the unnecessary conjunction. Such simplifications are widely used in logic circuit design to minimize gates, as redundant terms correspond to avoidable hardware.[26] In the concrete example of the power set Boolean algebra for a set , where is union, is intersection, and the order ≤ corresponds to set inclusion, the monotonicity and absorption laws align directly with subset relations. If , then and , preserving inclusion. Absorption manifests as and , illustrating how subsets absorb unions or intersections in set theory. This isomorphism underscores the abstract laws' intuitive basis in set operations.Duality and Completeness
In Boolean algebra, the duality principle asserts that every valid identity remains valid when conjunction (∧) is replaced by disjunction (∨), disjunction by conjunction, the constant 0 by 1, and 1 by 0, while negation (¬) remains unchanged.[27] This transformation preserves the equivalence of expressions, allowing the dual of any theorem to be derived directly from the original. For instance, the identity has dual .[27] De Morgan's laws exemplify this principle: the dual of is .[28] These laws, which interrelate negation with the binary operations, follow from the duality by applying the replacements to one form to obtain the other.[28] Additionally, double negation elimination, , is self-dual under this principle, as the transformation yields the same identity.[27] Boolean algebra is functionally complete, meaning the set of operations {∧, ∨, ¬} can express any possible Boolean function from variables to {0, 1}.[29] This completeness ensures that every truth table can be realized by a formula using only these operations. A proof sketch relies on disjunctive normal form (DNF): for a function that outputs 1 on certain input assignments, form the minterms corresponding to those assignments—each a conjunction of literals (variables or their negations)—and take their disjunction. For example, if only when and , then .[29] This construction covers all cases where , and evaluates to 0 elsewhere due to the properties of ∧ and ∨.[29]Representations
Diagrammatic Representations
Diagrammatic representations provide visual aids for understanding and manipulating Boolean expressions, enhancing intuition by depicting logical relationships through geometric or symbolic means. These tools translate abstract operations into concrete images, facilitating educational applications and preliminary design in logic systems.[30] Venn diagrams, introduced by John Venn in 1880, use overlapping circles to represent sets corresponding to Boolean variables, where the union of sets illustrates the OR operation, the intersection the AND operation, and the complement (shaded exterior) the NOT operation. For instance, the AND operation is shown as the shaded region within both overlapping circles for variables and .[31] Such diagrams align with truth tables by visually partitioning outcomes based on input combinations.[32] However, Venn diagrams become impractical for more than three variables, as constructing symmetric, non-intersecting regions for four or more sets requires complex curves or asymmetrical layouts that obscure clarity.[33][30] Logic gates offer standardized symbols for Boolean operations in digital circuit diagrams, where the AND gate resembles a rounded D-shape, the OR gate a pointed variant, and the NOT gate a triangle with a circle. Additional gates include the NAND (AND with NOT) and NOR (OR with NOT), each correlating to truth table outputs for their respective functions. These symbols abstractly represent Boolean algebra in schematic form, aiding visualization of expression evaluation.[34][32] Karnaugh maps, developed by Maurice Karnaugh in 1953, serve as grid-based diagrams for simplifying Boolean functions by grouping adjacent 1s in a tabular arrangement of minterms, minimizing the number of literals in the resulting expression. This method exploits the Gray code adjacency to eliminate redundant terms visually, providing an intuitive alternative to algebraic manipulation for functions up to six variables.[35] For example, Venn diagrams illustrate De Morgan's laws: the complement of the union shades the non-overlapping regions outside both circles, equivalent to the intersection of complements . Similarly, a half-adder circuit diagram uses an XOR gate for the sum output () and an AND gate for the carry (), demonstrating how gate symbols combine to realize arithmetic Boolean functions./02:_Logic/2.06:_De_Morgans_Laws)[36]Concrete Boolean Algebras
Concrete Boolean algebras provide specific instances that embody the abstract structure of Boolean algebras, making the concepts accessible through familiar mathematical objects. One of the most fundamental examples is the power set algebra: for any set , the collection of all subsets of , denoted , forms a Boolean algebra where the join operation is set union, the meet operation is set intersection, and the complement for is the set of elements in excluding those in ; the bottom element is the empty set , and the top element is itself.[37] This structure satisfies all Boolean algebra axioms, with the partial order induced by inclusion .[38] Another concrete realization arises in computing through bit vectors, which are fixed-length sequences of bits from the set . For an -bit vector, the elements are all possible binary strings of length , forming the Boolean algebra under component-wise operations: bitwise AND for , bitwise OR for , and bitwise NOT for ; the zero vector is the all-zero string, and the unit is the all-one string.[39] These operations align with the Boolean algebra properties, enabling efficient representation of finite sets or masks in digital systems, where each bit position corresponds to membership in a subset of .[40] The simplest nonzero Boolean algebra is the two-element structure , serving as the prototypical case with operations defined by the standard truth tables: , , , and similarly for (reversed for 1 and 0), while and .[41] Here, represents falsity and truth, directly mirroring classical two-valued logic.[38] This algebra generates the variety of all Boolean algebras, as every Boolean algebra is a subdirect product of copies of .[41] For a concrete finite example, consider the power set , which has four elements: , , , and . The operations include (union), (intersection), and (complement relative to ).[42] This algebra is atomic with two atoms and , illustrating how power set structures scale with the cardinality of the base set.[38] Infinite concrete Boolean algebras also exist, such as the free Boolean algebra on generators, which consists of all equivalence classes of Boolean terms built from variables under the Boolean operations, yielding distinct elements for finite .[43] This algebra is the initial object in the category of Boolean algebras, freely generated without relations beyond the axioms.[44]Formal Structure
Definition of Boolean Algebra
A Boolean algebra is an algebraic structure consisting of a set together with two binary operations, typically denoted (meet or conjunction) and (join or disjunction), a unary operation (complement or negation), and two distinguished constants (bottom or false) and (top or true).[45][22] These operations and constants satisfy the following core properties: commutativity (, ), associativity (, ), absorption (, ), distributivity (, ), and complement laws (, , , ).[45][22] These axioms ensure that every element has a unique complement and that the structure behaves consistently under the operations.[45] The structure induces a partial order on defined by if and only if (equivalently, ).[45][22] Under this order, forms a bounded lattice, where is the meet (greatest lower bound), is the join (least upper bound), is the least element, and is the greatest element.[45] Moreover, the complement operation provides relative complements: for any with , there exists a unique such that and .[22] This lattice perspective highlights Boolean algebras as complemented distributive lattices.[45] A homomorphism between Boolean algebras and is a function that preserves the operations and constants: , , , , and .[45][38] A subalgebra of is a subset containing and , closed under , , and , which thereby forms a Boolean algebra under the restricted operations.[45][38] Quotients of are constructed by factoring through ideals or filters; for instance, if is an ideal of , the quotient consists of cosets with induced operations, forming another Boolean algebra.[45] Boolean algebras may be finite or infinite. Finite Boolean algebras are atomic, meaning every element is a join of atoms (minimal nonzero elements), and they are isomorphic to the power set algebra of a finite set.[45] Infinite Boolean algebras can be atomic—for example, the power set algebra of an infinite set—or atomless—for example, the free Boolean algebra on countably many generators.[45]Axiomatization
Boolean algebra can be axiomatized through minimal sets of postulates that generate all its properties as theorems. One foundational formulation was provided by Edward V. Huntington in 1904, who developed independent sets of postulates defining the structure as a complemented distributive lattice. Huntington's first set includes closure under the operations of join (∨) and meet (∧), the existence of identities 0 and 1, commutativity of both operations, associativity, distributivity in both directions—such as —absorption laws like , and the existence of complements for every element , satisfying and .[46] A key variant in his framework emphasizes the medial property or a specialized distributivity, such as , which, together with absorption and complement existence, suffices to derive the full distributive lattice structure with complements. Another influential axiomatization views Boolean algebras through the lens of Boolean rings, where the structure is defined as a commutative ring of characteristic 2 in which every element is idempotent, i.e., for all .[45] Here, addition corresponds to symmetric difference (), multiplication to meet (), and the idempotence axiom ensures , capturing the exclusive-or nature without explicit complements. This ring-theoretic approach requires only the standard ring axioms (associativity, distributivity, commutativity, identities) plus idempotence, providing an alternative minimal basis equivalent to the lattice formulation.[47] The equivalence between these axiomatizations—lattice-based and ring-based—is established by mutual interpretability: from a Boolean ring, one defines join as and complement as , recovering the lattice operations while preserving all laws; conversely, from a lattice, symmetric difference and meet yield the ring structure.[45] All standard laws, such as De Morgan's theorems and the absorption identities, derive as theorems from either minimal set, ensuring completeness.[48] A pivotal result linking axiomatization to representability is Stone's representation theorem (1936), which states that every Boolean algebra is isomorphic to a field of sets, specifically the algebra of clopen subsets of a totally disconnected compact Hausdorff space known as its Stone space.[49] This theorem implies that any abstract Boolean algebra satisfying the axioms can be concretely realized as a subalgebra of a power set, with union, intersection, and complement corresponding to set operations, thereby validating the generative power of the postulates.[48] Modern extensions build on these foundations, such as cylindric algebras introduced by Alfred Tarski and collaborators in the mid-20th century, which augment Boolean algebras with cylindrification operators to model first-order logic quantifiers, enabling algebraic treatments of substitution and equality.[50] In category theory, Boolean algebras form the category BoolAlg of objects preserving finite meets and joins, with recent work (as of 2025) exploring Boolean doctrines over small categories as many-sorted algebras for higher-order logical structures.[51] These developments, including explorations of quantum analogs like orthomodular lattices, extend the axiomatic framework without altering the classical core.[52]Logical Connections
Relation to Propositional Logic
Boolean algebra provides a foundational algebraic semantics for classical propositional logic, where propositional variables correspond directly to generators in the Boolean algebra, and the logical connectives—conjunction (∧), disjunction (∨), and negation (¬)—mirror the algebraic operations of meet, join, and complement, respectively.[53] This correspondence establishes an isomorphism between the free Boolean algebra generated by the propositional variables and the Lindenbaum–Tarski algebra of propositional formulas modulo logical equivalence.[54] Truth assignments in propositional logic, which map propositions to truth values {true, false} or {1, 0}, function as homomorphisms from this algebra to the two-element Boolean algebra {0, 1}, preserving the structure of the operations.[53] Semantic entailment in propositional logic aligns with the partial order of the Boolean algebra: a formula semantically entails a formula if and only if, for every truth assignment (or homomorphism to {0, 1}), the valuation of is less than or equal to the valuation of in the lattice order—meaning whenever evaluates to 1, so does .[54] In the broader algebraic setting, this extends to arbitrary Boolean algebras, where entailment corresponds to the order relation between elements representing the formulas.[55] Tautologies, or logically valid formulas, emerge as the identities in the Lindenbaum–Tarski algebra, which is the quotient of the term algebra of propositional formulas by the congruence of logical equivalence; this algebra is freely generated by the propositional variables and satisfies all Boolean axioms.[53] Every propositional formula admits equivalent representations in disjunctive normal form (DNF), a disjunction of conjunctions of literals, or conjunctive normal form (CNF), a conjunction of disjunctions of literals; these serve as canonical forms analogous to the sum-of-products and product-of-sums expressions in Boolean algebra.[56] Such normal forms facilitate the algebraic simplification of formulas and underscore the completeness of Boolean operations in expressing all possible truth functions.[57] The interplay ensures soundness and completeness: the algebraic semantics of Boolean algebras is sound with respect to propositional logic, as every identity provable in the algebra corresponds to a logical validity, and complete, as every valid propositional inference is captured by an algebraic identity in the variety of Boolean algebras. This equivalence, formalized through the algebraization framework, confirms that Boolean algebra fully models the valid inferences of classical propositional logic without omission or excess.[54]Deductive Systems
Deductive systems for Boolean algebra are formal frameworks that enable the syntactic derivation of theorems in propositional logic, where propositions correspond to elements of a Boolean algebra and logical connectives to algebraic operations. These systems establish the provability of identities that hold under Boolean semantics, ensuring that derivations mirror the valid equalities in the algebra. Key examples include Hilbert-style systems, sequent calculi, and natural deduction, each providing distinct rules for constructing proofs while achieving equivalence to Boolean tautologies. The Hilbert-style system, formalized by David Hilbert and Wilhelm Ackermann, relies on a minimal set of axiom schemas for implication and negation, combined with the single inference rule of modus ponens. The axioms are: Modus ponens allows inference of from premises and .[58] This system captures classical propositional logic, with conjunction, disjunction, and other connectives defined in terms of implication and negation (e.g., ). Completeness was established by Paul Bernays, demonstrating that every Boolean tautology—interpreted as a valid implication where is a tautology—is provable.[59] Sequent calculus, introduced by Gerhard Gentzen, represents derivations using sequents of the form , where and are multisets of formulas indicating assumptions and conclusions, respectively. Logical rules include introduction and elimination for connectives: for conjunction, right introduction is , and left elimination is (similarly for ); analogous rules apply to disjunction and negation, such as right negation . Structural rules like weakening () and contraction ensure flexibility in managing assumptions. For classical logic, an additional rule or axiom handles excluded middle. This framework facilitates analytic proofs by decomposing formulas bottom-up. Natural deduction, also pioneered by Gentzen, emphasizes inference rules that directly mirror Boolean operations through introduction and elimination pairs. For conjunction, introduction combines premises and to yield , while elimination projects or from ; disjunction introduction adds or to form , with elimination using cases; negation introduction assumes to derive contradiction and conclude , and elimination from and yields contradiction. These rules, along with discharge of assumptions, produce tree-like proofs that closely resemble informal reasoning. The system supports classical extensions via rules like double negation elimination. The theorems derivable in these systems coincide precisely with Boolean identities, as soundness ensures provable formulas are semantically valid under Boolean valuations, and completeness guarantees the converse: every identity holds if and only if it is a theorem. This equivalence links syntactic deduction to the algebraic structure of Boolean lattices.[59] A concrete example is the derivation of De Morgan's law in the Hilbert-style system, which proceeds via a chain of implications using the axioms and modus ponens. Start with the third axiom instantiated as , then apply substitutions and the first two axioms to reduce contrapositives and distribute implications, ultimately yielding the target after several steps involving double negations and equivalence definitions. Such derivations confirm the system's ability to generate all Boolean dualities. In sequent calculus, completeness follows from Gentzen's cut-elimination theorem (Hauptsatz), which proves that any proof using the cut rule (similar to transitivity) can be transformed into an equivalent cut-free proof, ensuring all valid sequents are derivable without circular reasoning. This normalization underpins the analytic nature of the system for Boolean verification.Applications
Computing and Digital Logic
Boolean algebra underpins the design and operation of digital circuits, providing a mathematical framework for representing and manipulating binary signals in computing hardware. In his seminal 1938 master's thesis, Claude Shannon established the equivalence between Boolean operations and electrical switching circuits, showing how relays could implement logical functions like conjunction (AND) and disjunction (OR), thereby laying the groundwork for electronic digital computation.[60] This connection transformed abstract logic into practical engineering, enabling the development of computers where binary states—0 and 1—correspond to voltage levels in transistors. Logic gates serve as the physical realizations of Boolean operations, fabricated using semiconductor technology to perform AND, OR, NOT, XOR, and other functions at high speeds. Circuits are classified as combinational, where outputs are determined solely by current inputs via Boolean expressions (e.g., multiplexers for data routing), or sequential, which use feedback through storage elements to depend on both current and past inputs (e.g., registers in processors).[60] In modern hardware as of 2025, these gates form the basis of field-programmable gate arrays (FPGAs), which allow reconfigurable Boolean logic for custom acceleration, and graphics processing units (GPUs), where parallel arrays of gates execute bitwise operations in shaders and tensor cores for tasks like rendering and machine learning.[61][62] To optimize circuit efficiency, Boolean minimization techniques reduce the number of gates and interconnections needed to implement a function. The Karnaugh map, introduced by Maurice Karnaugh in 1953, visualizes truth tables as a grid where adjacent cells differing by one variable allow grouping of minterms to simplify expressions to sum-of-products form.[63] For more variables, the Quine-McCluskey algorithm, developed by Willard Quine in 1952 and extended by Edward McCluskey in 1956, systematically identifies prime implicants through tabular comparison, yielding minimal covers suitable for automation in electronic design automation tools.[64][65] These methods minimize propagation delays and power consumption, critical for high-density chips. Binary arithmetic in digital systems relies on Boolean operations to perform addition, subtraction, and multiplication. A half-adder, the basic building block for multi-bit adders, computes the sum and carry of two bits and using: This circuit employs an XOR gate for the sum (exclusive or) and an AND gate for the carry, as verified in standard combinational logic design.[66] Full adders extend this by incorporating a carry-in bit, enabling ripple-carry or carry-lookahead adders in processors; multipliers cascade AND gates for partial products and adders for summation, all derived from Boolean minimization. In software, Boolean algebra manifests through bitwise operators and boolean types in programming languages. In C++, the operators& (bitwise AND), | (bitwise OR), ^ (bitwise XOR), and ~ (bitwise NOT) apply Boolean functions to integer bits, supporting low-level manipulations like masking and bit shifting for efficient algorithms in systems programming.[67] Boolean variables (true/false) drive conditional statements, directly implementing propositional logic for control flow in applications from embedded systems to high-performance computing.
Two-level logic implementations, such as sum-of-products (AND-OR) or product-of-sums (OR-AND), realize minimized Boolean functions but can introduce hazards—transient glitches due to timing variations in gate delays. Edward McCluskey developed the modern theory of these static and dynamic hazards in the 1950s at Bell Labs, showing how multiple input changes can cause erroneous outputs unless covered by redundant terms.[68] Hazard-free designs, essential for reliable operation in FPGAs and GPUs, use techniques like adding consensus terms to ensure monotonic transitions, balancing minimization with timing robustness.











































