Snub triapeirogonal tiling

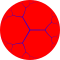
Snub triapeirogonal tiling
Poincaré disk model of the hyperbolic plane
Type	Hyperbolic uniform tiling
Vertex configuration	3.3.3.3.∞
Schläfli symbol	sr{∞,3} or ${\displaystyle s{\begin{Bmatrix}\infty \\3\end{Bmatrix}}}$
Wythoff symbol	| ∞ 3 2
Coxeter diagram	or
Symmetry group	[∞,3]+, (∞32)
Dual	Order-3-infinite floret pentagonal tiling
Properties	Vertex-transitive Chiral

In geometry, the snub triapeirogonal tiling is a uniform tiling of the hyperbolic plane with a Schläfli symbol of sr{∞,3}.

Drawn in chiral pairs, with edges missing between black triangles:

The dual tiling:

This hyperbolic tiling is topologically related as a part of sequence of uniform snub polyhedra with vertex configurations (3.3.3.3.n), and [n,3] Coxeter group symmetry.

n32 symmetry mutations of snub tilings: 3.3.3.3.n v t e
Symmetry n32	Spherical				Euclidean	Compact hyperbolic		Paracomp.
	232	332	432	532	632	732	832	∞32
Snub figures
Config.	3.3.3.3.2	3.3.3.3.3	3.3.3.3.4	3.3.3.3.5	3.3.3.3.6	3.3.3.3.7	3.3.3.3.8	3.3.3.3.∞
Gyro figures
Config.	V3.3.3.3.2	V3.3.3.3.3	V3.3.3.3.4	V3.3.3.3.5	V3.3.3.3.6	V3.3.3.3.7	V3.3.3.3.8	V3.3.3.3.∞

Paracompact uniform tilings in [∞,3] family v t e
Symmetry: [∞,3], (*∞32)							[∞,3]+ (∞32)	[1+,∞,3] (*∞33)		[∞,3+] (3*∞)
		=	=	=				= or	= or	=
{∞,3}	t{∞,3}	r{∞,3}	t{3,∞}	{3,∞}	rr{∞,3}	tr{∞,3}	sr{∞,3}	h{∞,3}	h2{∞,3}	s{3,∞}
Uniform duals
V∞3	V3.∞.∞	V(3.∞)2	V6.6.∞	V3∞	V4.3.4.∞	V4.6.∞	V3.3.3.3.∞	V(3.∞)3		V3.3.3.3.3.∞

• List of uniform planar tilings
• Tilings of regular polygons
• Uniform tilings in hyperbolic plane

• Weisstein, Eric W. "Hyperbolic tiling". MathWorld.
• Weisstein, Eric W. "Poincaré hyperbolic disk". MathWorld.

This hyperbolic geometry-related article is a stub. You can help Wikipedia by expanding it.

• v
• t
• e