Penrose tiling

Covering a flat surface ("the plane") with some pattern of geometric shapes ("tiles"), with no overlaps or gaps, is called a tiling. The most familiar tilings, such as covering a floor with squares meeting edge-to-edge, are examples of periodic tilings. If a square tiling is shifted by the width of a tile, parallel to the sides of the tile, the result is the same pattern of tiles as before the shift. A shift (formally, a translation) that preserves the tiling in this way is called a period of the tiling. A tiling is called periodic when it has periods that shift the tiling in two different directions.^[5]

The tiles in the square tiling have only one shape, and it is common for other tilings to have only a finite number of shapes. These shapes are called prototiles, and a set of prototiles is said to admit a tiling or tile the plane if there is a tiling of the plane using only these shapes. That is, each tile in the tiling must be congruent to one of these prototiles.^[6]

A tiling that has no periods is non-periodic. A set of prototiles is said to be aperiodic if all of its tilings are non-periodic, and in this case its tilings are also called aperiodic tilings.^[7] Penrose tilings are among the simplest known examples of aperiodic tilings of the plane by finite sets of prototiles.^[5]

The subject of aperiodic tilings received new interest in the 1960s when logician Hao Wang noted connections between decision problems and tilings.^[9] In particular, he introduced tilings by square plates with colored edges, now known as Wang dominoes or tiles, and posed the "Domino Problem": to determine whether a given set of Wang dominoes could tile the plane with matching colors on adjacent domino edges. He observed that if this problem were undecidable, then there would have to exist an aperiodic set of Wang dominoes. At the time, this seemed implausible, so Wang conjectured no such set could exist.

Wang's student Robert Berger proved that the Domino Problem was undecidable (so Wang's conjecture was incorrect) in his 1964 thesis,^[10] and obtained an aperiodic set of 20,426 Wang dominoes.^[11] He also described a reduction to 104 such prototiles; the latter did not appear in his published monograph,^[12] but in 1968, Donald Knuth detailed a modification of Berger's set requiring only 92 dominoes.^[13]

The color matching required in a tiling by Wang dominoes can easily be achieved by modifying the edges of the tiles like jigsaw puzzle pieces so that they can fit together only as prescribed by the edge colorings.^[14] Raphael Robinson, in a 1971 paper^[15] which simplified Berger's techniques and undecidability proof, used this technique to obtain an aperiodic set of just six prototiles.^[16]

The first Penrose tiling (tiling P1 below) is an aperiodic set of six prototiles, introduced by Roger Penrose in a 1974 paper,^[18] based on pentagons rather than squares. Any attempt to tile the plane with regular pentagons necessarily leaves gaps, but Johannes Kepler showed, in his 1619 work Harmonices Mundi, that these gaps can be filled using pentagrams (star polygons), decagons and related shapes.^[19] Kepler extended this tiling by five polygons and found no periodic patterns, and already conjectured that every extension would introduce a new feature^[20] hence creating an aperiodic tiling. Traces of these ideas can also be found in the work of Albrecht Dürer.^[21] Acknowledging inspiration from Kepler, Penrose found matching rules for these shapes, obtaining an aperiodic set. These matching rules can be imposed by decorations of the edges, as with the Wang tiles. Penrose's tiling can be viewed as a completion of Kepler's finite Aa pattern.^[22]

Penrose subsequently reduced the number of prototiles to two, discovering the kite and dart tiling (tiling P2 below) and the rhombus tiling (tiling P3 below).^[23] The rhombus tiling was independently discovered by Robert Ammann in 1976.^[24] Penrose and John H. Conway investigated the properties of Penrose tilings, and discovered that a substitution property explained their hierarchical nature; their findings were publicized by Martin Gardner in his January 1977 "Mathematical Games" column in Scientific American.^[25]

In 1981, N. G. de Bruijn provided two different methods to construct Penrose tilings. De Bruijn's "multigrid method" obtains the Penrose tilings as the dual graphs of arrangements of five families of parallel lines. In his "cut and project method", Penrose tilings are obtained as two-dimensional projections from a five-dimensional cubic structure. In these approaches, the Penrose tiling is viewed as a set of points, its vertices, while the tiles are geometrical shapes obtained by connecting vertices with edges.^[26] A 1990 construction by Baake, Kramer, Schlottmann, and Zeidler derived the Penrose tiling and the related Tübingen triangle tiling in a similar manner from the four-dimensional 5-cell honeycomb.^[27]

The three types of Penrose tiling, P1–P3, are described individually below.^[28] They have many common features: in each case, the tiles are constructed from shapes related to the pentagon (and hence to the golden ratio), but the basic tile shapes need to be supplemented by matching rules in order to tile aperiodically. These rules may be described using labeled vertices or edges, or patterns on the tile faces; alternatively, the edge profile can be modified (e.g. by indentations and protrusions) to obtain an aperiodic set of prototiles.^[11][29]

Penrose's first tiling uses pentagons and three other shapes: a five-pointed "star" (a pentagram), a "boat" (also known as a "justice cap",^[30] roughly 3/5 of a star) and a "diamond" (a thin rhombus).^[31] To ensure that all tilings are non-periodic, there are matching rules that specify how tiles may meet each other, and there are three different types of matching rule for the pentagonal tiles. Treating these three types as different prototiles gives a set of six prototiles overall. It is common to indicate the three different types of pentagonal tiles using three different colors, as in the figure above right.^[32]

Penrose's second tiling uses quadrilaterals called the "kite" and "dart", which may be combined to make a rhombus. However, the matching rules prohibit such a combination.^[33] Both the kite and dart are composed of two triangles, called Robinson triangles, after 1975 notes by Robinson.^[34]

Kite and dart tiles (top) and the seven possible vertex figures in a P2 tiling, which are each given nicknames as follows – First row: star, ace, sun. Second row: king, jack, queen, deuce

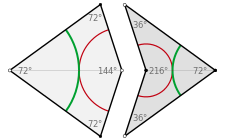
• The kite is a quadrilateral whose four interior angles are 72, 72, 72, and 144 degrees. The kite may be bisected along its axis of symmetry to form a pair of acute Robinson triangles (with angles of 36, 72 and 72 degrees).
• The dart is a non-convex quadrilateral whose four interior angles are 36, 72, 36, and 216 degrees. The dart may be bisected along its axis of symmetry to form a pair of obtuse Robinson triangles (with angles of 36, 36 and 108 degrees), which are smaller than the acute triangles.

The matching rules can be described in several ways. One approach is to color the vertices (with two colors, e.g., black and white) and require that adjacent tiles have matching vertices.^[35] Another is to use a pattern of circular arcs (as shown above left in green and red) to constrain the placement of tiles: when two tiles share an edge in a tiling, the patterns must match at these edges.^[23]

These rules often force the placement of certain tiles: for example, the concave vertex of any dart is necessarily filled by two kites. The corresponding figure (center of the top row in the lower image on the left) is called an "ace" by Conway; although it looks like an enlarged kite, it does not tile in the same way.^[36] Similarly the concave vertex formed when two kites meet along a short edge is necessarily filled by two darts (bottom right). In fact, there are only seven possible ways for the tiles to meet at a vertex; two of these figures – namely, the "star" (top left) and the "sun" (top right) – have 5-fold dihedral symmetry (by rotations and reflections), while the remainder have a single axis of reflection (vertical in the image).^[37] Apart from the ace (top middle) and the sun, all of these vertex figures force the placement of additional tiles.^[38]

The third tiling uses a pair of rhombuses (often referred to as "rhombs" in this context) with equal sides but different angles.^[11] Ordinary rhombus-shaped tiles can be used to tile the plane periodically, so restrictions must be made on how tiles can be assembled: no two tiles may form a parallelogram, as this would allow a periodic tiling, but this constraint is not sufficient to force aperiodicity, as figure 1 above shows.

There are two kinds of tile, both of which can be decomposed into Robinson triangles.^[34]

• The thin rhomb t has four corners with angles of 36, 144, 36, and 144 degrees. The t rhomb may be bisected along its short diagonal to form a pair of acute Robinson triangles.
• The thick rhomb T has angles of 72, 108, 72, and 108 degrees. The T rhomb may be bisected along its long diagonal to form a pair of obtuse Robinson triangles; in contrast to the P2 tiling, these are larger than the acute triangles.

The matching rules distinguish sides of the tiles, and entail that tiles may be juxtaposed in certain particular ways but not in others. Two ways to describe these matching rules are shown in the image on the right. In one form, tiles must be assembled such that the curves on the faces match in color and position across an edge. In the other, tiles must be assembled such that the bumps on their edges fit together.^[11]

There are 54 cyclically ordered combinations of such angles that add up to 360 degrees at a vertex, but the rules of the tiling allow only seven of these combinations to appear (although one of these arises in two ways).^[39]

The various combinations of angles and facial curvature allow construction of arbitrarily complex tiles, such as the Penrose chickens.^[40]

Several properties and common features of the Penrose tilings involve the golden ratio ${\displaystyle \varphi ={\frac {1+{\sqrt {5}}}{2}}}$ (approximately 1.618).^[34][35] This is the ratio of chord lengths to side lengths in a regular pentagon, and satisfies φ = 1 + 1/φ.

Consequently, the ratio of the lengths of long sides to short sides in the (isosceles) Robinson triangles is φ:1. It follows that the ratio of long side lengths to short in both kite and dart tiles is also φ:1, as are the length ratios of sides to the short diagonal in the thin rhomb t, and of long diagonal to sides in the thick rhomb T. In both the P2 and P3 tilings, the ratio of the area of the larger Robinson triangle to the smaller one is φ:1, hence so are the ratios of the areas of the kite to the dart, and of the thick rhomb to the thin rhomb. (Both larger and smaller obtuse Robinson triangles can be found in the pentagon on the left: the larger triangles at the top – the halves of the thick rhomb – have linear dimensions scaled up by φ compared to the small shaded triangle at the base, and so the ratio of areas is φ²:1.)

Any Penrose tiling has local pentagonal symmetry, in the sense that there are points in the tiling surrounded by a symmetric configuration of tiles: such configurations have fivefold rotational symmetry about the center point, as well as five mirror lines of reflection symmetry passing through the point, a dihedral symmetry group.^[11] This symmetry will generally preserve only a patch of tiles around the center point, but the patch can be very large: Conway and Penrose proved that whenever the colored curves on the P2 or P3 tilings close in a loop, the region within the loop has pentagonal symmetry, and furthermore, in any tiling, there are at most two such curves of each color that do not close up.^[41]

There can be at most one center point of global fivefold symmetry: if there were more than one, then rotating each about the other would yield two closer centers of fivefold symmetry, which leads to a mathematical contradiction.^[42] There are only two Penrose tilings (of each type) with global pentagonal symmetry: for the P2 tiling by kites and darts, the center point is either a "sun" or "star" vertex.^[43]

Many of the common features of Penrose tilings follow from a hierarchical pentagonal structure given by substitution rules: this is often referred to as inflation and deflation, or composition and decomposition, of tilings or (collections of) tiles.^[11][25][44] The substitution rules decompose each tile into smaller tiles of the same shape as those used in the tiling (and thus allow larger tiles to be "composed" from smaller ones). This shows that the Penrose tiling has a scaling self-similarity, and so can be thought of as a fractal, using the same process as the pentaflake.^[45]

Penrose originally discovered the P1 tiling in this way, by decomposing a pentagon into six smaller pentagons (one half of a net of a dodecahedron) and five half-diamonds; he then observed that when he repeated this process the gaps between pentagons could all be filled by stars, diamonds, boats (or "justice caps"^[30], as he puts it) and other pentagons.^[31] By iterating this process indefinitely he obtained one of the two P1 tilings with pentagonal symmetry.^[11][22]

The substitution method for both P2 and P3 tilings can be described using Robinson triangles of different sizes. The Robinson triangles arising in P2 tilings (by bisecting kites and darts) are called A-tiles, while those arising in the P3 tilings (by bisecting rhombs) are called B-tiles.^[34] The smaller A-tile, denoted A_S, is an obtuse Robinson triangle, while the larger A-tile, A_L, is acute; in contrast, a smaller B-tile, denoted B_S, is an acute Robinson triangle, while the larger B-tile, B_L, is obtuse.

Concretely, if A_S has side lengths (1, 1, φ), then A_L has side lengths (φ, φ, 1). B-tiles can be related to such A-tiles in two ways:

• If B_S has the same size as A_L then B_L is an enlarged version φA_S of A_S, with side lengths (φ, φ, φ² = 1 + φ) – this decomposes into an A_L tile and A_S tile joined along a common side of length 1.
• If instead B_L is identified with A_S, then B_S is a reduced version (1/φ)A_L of A_L with side lengths (1/φ,1/φ,1) – joining a B_S tile and a B_L tile along a common side of length 1 then yields (a decomposition of) an A_L tile.

In these decompositions, there appears to be an ambiguity: Robinson triangles may be decomposed in two ways, which are mirror images of each other in the (isosceles) axis of symmetry of the triangle. In a Penrose tiling, this choice is fixed by the matching rules. Furthermore, the matching rules also determine how the smaller triangles in the tiling compose to give larger ones.^[34]

Partial inflation of star to yield rhombs, and of a collection of rhombs to yield an ace.

It follows that the P2 and P3 tilings are mutually locally derivable: a tiling by one set of tiles can be used to generate a tiling by another. For example, a tiling by kites and darts may be subdivided into A-tiles, and these can be composed in a canonical way to form B-tiles and hence rhombs.^[17] The P2 and P3 tilings are also both mutually locally derivable with the P1 tiling (see figure 2 above).^[46]

The decomposition of B-tiles into A-tiles may be written

B_S = A_L, B_L = A_L + A_S

(assuming the larger size convention for the B-tiles), which can be summarized in a substitution matrix equation:^[47]

${\displaystyle {\begin{pmatrix}B_{L}\\B_{S}\end{pmatrix}}={\begin{pmatrix}1&1\\1&0\end{pmatrix}}{\begin{pmatrix}A_{L}\\A_{S}\end{pmatrix}}\,.}$

Combining this with the decomposition of enlarged φA-tiles into B-tiles yields the substitution

${\displaystyle {\begin{pmatrix}\varphi A_{L}\\\varphi A_{S}\end{pmatrix}}={\begin{pmatrix}1&1\\1&0\end{pmatrix}}{\begin{pmatrix}B_{L}\\B_{S}\end{pmatrix}}={\begin{pmatrix}2&1\\1&1\end{pmatrix}}{\begin{pmatrix}A_{L}\\A_{S}\end{pmatrix}}\,,}$

so that the enlarged tile φA_L decomposes into two A_L tiles and one A_S tiles. The matching rules force a particular substitution: the two A_L tiles in a φA_L tile must form a kite, and thus a kite decomposes into two kites and a two half-darts, and a dart decomposes into a kite and two half-darts.^[48][49] Enlarged φB-tiles decompose into B-tiles in a similar way (via φA-tiles).

Composition and decomposition can be iterated, so that, for example

${\displaystyle \varphi ^{n}{\begin{pmatrix}A_{L}\\A_{S}\end{pmatrix}}={\begin{pmatrix}2&1\\1&1\end{pmatrix}}^{n}{\begin{pmatrix}A_{L}\\A_{S}\end{pmatrix}}\,.}$

The number of kites and darts in the nth iteration of the construction is determined by the nth power of the substitution matrix:

${\displaystyle {\begin{pmatrix}2&1\\1&1\end{pmatrix}}^{n}={\begin{pmatrix}F_{2n+1}&F_{2n}\\F_{2n}&F_{2n-1}\end{pmatrix}}\,,}$

where F_n is the nth Fibonacci number. The ratio of numbers of kites to darts in any sufficiently large P2 Penrose tiling pattern therefore approximates to the golden ratio φ.^[50] A similar result holds for the ratio of the number of thick rhombs to thin rhombs in the P3 Penrose tiling.^[48]

Consecutive deflations of the 'sun' vertex in a Penrose tiling of type P2

Consecutive deflations of a tile-set in a Penrose tiling of type P3

8th deflation of the 'sun' vertex in a Penrose tiling of type P2

Starting with a collection of tiles from a given tiling (which might be a single tile, a tiling of the plane, or any other collection), deflation proceeds with a sequence of steps called generations. In one generation of deflation, each tile is replaced with two or more new tiles that are scaled-down versions of tiles used in the original tiling. The substitution rules guarantee that the new tiles will be arranged in accordance with the matching rules.^[48] Repeated generations of deflation produce a tiling of the original axiom shape with smaller and smaller tiles.

This rule for dividing the tiles is a subdivision rule.

One step of the substitution rules for kite and dart Penrose tiles.

Four iterations of the kite and dart substitutions.

Name	Initial tiles	Generation 1	Generation 2	Generation 3
Half-kite
Half-dart
Sun
Star

The above table should be used with caution. The half kite and half dart deflation are useful only in the context of deflating a larger pattern as shown in the sun and star deflations. They give incorrect results if applied to single kites and darts.

In addition, the simple subdivision rule generates holes near the edges of the tiling which are just visible in the top and bottom illustrations on the right. Additional forcing rules are useful.

Inflation and deflation yield a method for constructing kite and dart (P2) tilings, or rhombus (P3) tilings, known as up-down generation.^[36][48][49]

The Penrose tilings, being non-periodic, have no translational symmetry – the pattern cannot be shifted to match itself over the entire plane. However, any bounded region, no matter how large, will be repeated an infinite number of times within the tiling. Therefore, no finite patch can uniquely determine a full Penrose tiling, nor even determine which position within the tiling is being shown.^[51]

This shows in particular that the number of distinct Penrose tilings (of any type) is uncountably infinite. Up-down generation yields one method to parameterize the tilings, but other methods use Ammann bars, pentagrids, or cut and project schemes.^[48]

In 1996, German mathematician Petra Gummelt demonstrated that a covering (so called to distinguish it from a non-overlapping tiling) equivalent to the Penrose tiling can be constructed using a single decagonal tile if two kinds of overlapping regions are allowed.^[53] The decagonal tile is decorated with colored patches, and the covering rule allows only those overlaps compatible with the coloring. A suitable decomposition of the decagonal tile into kites and darts transforms such a covering into a Penrose (P2) tiling. Similarly, a P3 tiling can be obtained by inscribing a thick rhomb into each decagon; the remaining space is filled by thin rhombs.

These coverings have been considered as a realistic model for the growth of quasicrystals: the overlapping decagons are 'quasi-unit cells' analogous to the unit cells from which crystals are constructed, and the matching rules maximize the density of certain atomic clusters.^[52][54] The aperiodic nature of the coverings can make theoretical studies of physical properties, such as electronic structure, difficult due to the absence of Bloch's theorem. However, spectra of quasicrystals can still be computed with error control.^[55]

The three variants of the Penrose tiling are mutually locally derivable. Selecting some subsets from the vertices of a P1 tiling allows to produce other non-periodic tilings. If the corners of one pentagon in P1 are labeled in succession by 1,3,5,2,4 an unambiguous tagging in all the pentagons is established, the order being either clockwise or counterclockwise. Points with the same label define a tiling by Robinson triangles while points with the numbers 3 and 4 on them define the vertices of a Tie-and-Navette tiling.^[56]

There are also other related unequivalent tilings, such as the hexagon-boat-star and Mikulla–Roth tilings. For instance, if the matching rules for the rhombus tiling are reduced to a specific restriction on the angles permitted at each vertex, a binary tiling is obtained.^[57] Its underlying symmetry is also fivefold but it is not a quasicrystal. It can be obtained either by decorating the rhombs of the original tiling with smaller ones, or by applying substitution rules, but not by de Bruijn's cut-and-project method.^[58]

• 
  Pentagonal and decagonal Girih-tile pattern on a spandrel from the Darb-i Imam shrine, Isfahan, Iran (1453 C.E.)
• 
  Salesforce Transit Center in San Francisco. The outer "skin", made of white aluminum, is perforated in the pattern of a Penrose tiling.
• 
  Penrose tiling on the floor in Computer Center 3 (CC-3), IIIT Allahabad

The aesthetic value of tilings has long been appreciated, and remains a source of interest in them; hence the visual appearance (rather than the formal defining properties) of Penrose tilings has attracted attention. The similarity with certain decorative patterns used in North Africa and the Middle East has been noted;^[59][60] the physicists Peter J. Lu and Paul Steinhardt have presented evidence that a Penrose tiling underlies examples of medieval Islamic geometric patterns, such as the girih (strapwork) tilings at the Darb-e Imam shrine in Isfahan.^[61]

Artist Clark Richert used the same rhombs in artwork he was developing at Drop City in 1970 which he derived by projecting the rhombic triacontahedron shadow onto a plane and observing the embedded "fat" rhombi and "skinny" rhombi which tile together to produce the non-periodic tessellation, predating Penrose's discovery.^[62] These geometric explorations led to the development of Steve Baer's Zome Architecture. Art historian Martin Kemp has observed that Albrecht Dürer sketched similar motifs of a rhombus tiling.^[63]

In 1979, Miami University used a Penrose tiling executed in terrazzo to decorate the Bachelor Hall courtyard in their Department of Mathematics and Statistics.^[64]

In Indian Institute of Information Technology, Allahabad, since the first phase of construction in 2001, academic buildings were designed on the basis of "Penrose Geometry", styled on tessellations developed by Roger Penrose. In many places in those buildings, the floor has geometric patterns composed of Penrose tiling.^[65]

The floor of the atrium of the Bayliss Building at The University of Western Australia is tiled with Penrose tiles.^[66]

The Andrew Wiles Building, the location of the Mathematics Department at the University of Oxford as of October 2013,^[67] includes a section of Penrose tiling as the paving of its entrance.^[68]

The pedestrian part of the street Keskuskatu in central Helsinki is paved using a form of Penrose tiling. The work was finished in 2014.^[69]

San Francisco's 2018 Salesforce Transit Center features perforations in its exterior's undulating white metal skin in the Penrose pattern.^[70]

• Girih tiles
• List of aperiodic sets of tiles
• Pinwheel tiling
• Pentagonal tiling
• Quaquaversal tiling
• Tübingen triangle