Hubbry Logo
Version space learningVersion space learningMain
Open search
Version space learning
Community hub
Version space learning
logo
8 pages, 0 posts
0 subscribers
Be the first to start a discussion here.
Be the first to start a discussion here.
Version space learning
Version space learning
Version space learning
View on Wikipedia
from Wikipedia
Version space for a "rectangle" hypothesis language in two dimensions. Green pluses are positive examples, and red circles are negative examples. GB is the maximally general positive hypothesis boundary, and SB is the maximally specific positive hypothesis boundary. The intermediate (thin) rectangles represent the hypotheses in the version space.

Version space learning is a logical approach to machine learning, specifically binary classification. Version space learning algorithms search a predefined space of hypotheses, viewed as a set of logical sentences. Formally, the hypothesis space is a disjunction[1]

(i.e., one or more of hypotheses 1 through n are true). A version space learning algorithm is presented with examples, which it will use to restrict its hypothesis space; for each example x, the hypotheses that are inconsistent with x are removed from the space.[2] This iterative refining of the hypothesis space is called the candidate elimination algorithm, the hypothesis space maintained inside the algorithm, its version space.[1]

The version space algorithm

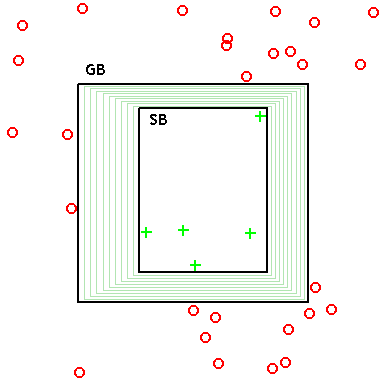
[edit]

In settings where there is a generality-ordering on hypotheses, it is possible to represent the version space by two sets of hypotheses: (1) the most specific consistent hypotheses, and (2) the most general consistent hypotheses, where "consistent" indicates agreement with observed data.

The most specific hypotheses (i.e., the specific boundary SB) cover the observed positive training examples, and as little of the remaining feature space as possible. These hypotheses, if reduced any further, exclude a positive training example, and hence become inconsistent. These minimal hypotheses essentially constitute a (pessimistic) claim that the true concept is defined just by the positive data already observed: Thus, if a novel (never-before-seen) data point is observed, it should be assumed to be negative. (I.e., if data has not previously been ruled in, then it's ruled out.)

The most general hypotheses (i.e., the general boundary GB) cover the observed positive training examples, but also cover as much of the remaining feature space without including any negative training examples. These, if enlarged any further, include a negative training example, and hence become inconsistent. These maximal hypotheses essentially constitute a (optimistic) claim that the true concept is defined just by the negative data already observed: Thus, if a novel (never-before-seen) data point is observed, it should be assumed to be positive. (I.e., if data has not previously been ruled out, then it's ruled in.)

Thus, during learning, the version space (which itself is a set – possibly infinite – containing all consistent hypotheses) can be represented by just its lower and upper bounds (maximally general and maximally specific hypothesis sets), and learning operations can be performed just on these representative sets.

After learning, classification can be performed on unseen examples by testing the hypothesis learned by the algorithm. If the example is consistent with multiple hypotheses, a majority vote rule can be applied.[1]

Historical background

[edit]

The notion of version spaces was introduced by Mitchell in the early 1980s[2] as a framework for understanding the basic problem of supervised learning within the context of solution search. Although the basic "candidate elimination" search method that accompanies the version space framework is not a popular learning algorithm, there are some practical implementations that have been developed (e.g., Sverdlik & Reynolds 1992, Hong & Tsang 1997, Dubois & Quafafou 2002).

A major drawback of version space learning is its inability to deal with noise: any pair of inconsistent examples can cause the version space to collapse, i.e., become empty, so that classification becomes impossible.[1] One solution of this problem is proposed by Dubois and Quafafou that proposed the Rough Version Space,[3] where rough sets based approximations are used to learn certain and possible hypothesis in the presence of inconsistent data.

See also

[edit]
  • Formal concept analysis
  • Inductive logic programming
  • Rough set. [The rough set framework focuses on the case where ambiguity is introduced by an impoverished feature set. That is, the target concept cannot be decisively described because the available feature set fails to disambiguate objects belonging to different categories. The version space framework focuses on the (classical induction) case where the ambiguity is introduced by an impoverished data set. That is, the target concept cannot be decisively described because the available data fails to uniquely pick out a hypothesis. Naturally, both types of ambiguity can occur in the same learning problem.]
  • Inductive reasoning. [On the general problem of induction.]

References

[edit]
Revisions and contributorsEdit on WikipediaRead on Wikipedia

Version space learning

View on Grokipedia
from Grokipedia
Version space learning is a foundational approach in for concept acquisition, where a learner identifies a target concept from a set of positive and negative examples by maintaining the —the complete set of in a predefined hypothesis H\mathcal{H} that are consistent with the observed data. Introduced by in 1977, this method assumes a partial ordering on hypotheses by generality, allowing efficient representation of the version space through its maximally general boundary GG (the most general consistent hypotheses) and maximally specific boundary SS (the most specific consistent hypotheses), without enumerating all possibilities. The technique is particularly suited to noise-free environments and conjunctive hypothesis spaces, enabling the learner to refine boundaries incrementally as new examples arrive. The core algorithm, known as the candidate-elimination algorithm, initializes GG with the most general hypothesis (e.g., the empty conjunction or ⊤\top) and SS with the most specific (e.g., ⊥\bot) before processing examples sequentially. For a positive example, inconsistent hypotheses in GG are removed, and SS is generalized by finding the minimal generalizations that cover the example while remaining more specific than GG; conversely, for a negative example, inconsistent hypotheses in SS are removed, and GG is specialized by replacing inconsistent general hypotheses with minimally more specific versions that do not cover the example. This boundary-based maintenance ensures the version space shrinks monotonically, converging to the target concept if it exists in H\mathcal{H} and the data is consistent, with computational efficiency leveraging the lattice structure of the hypothesis space where any consistent hypothesis lies between SS and GG. Originally applied in rule-learning systems like Meta-DENDRAL for discovering chemical inference rules from spectroscopic data, version space learning exemplifies early symbolic AI methods and has influenced subsequent work in and explainable AI. However, it relies on strong inductive biases, such as representable concepts and noise-free training, limiting its practicality for real-world noisy datasets or complex, non-conjunctive where the version space may not converge uniquely or efficiently. Despite these constraints, the framework provides a theoretically grounded basis for understanding generalization in , highlighting the trade-offs between hypothesis expressiveness and learning tractability.

Overview

Definition and Principles

Version space learning is a logical, symbolic technique employed in tasks to iteratively refine the hypothesis space based on observed examples. It maintains the set of all hypotheses that are consistent with the training data, thereby narrowing down potential models of the target concept without requiring exhaustive search through the entire hypothesis space. This approach is particularly suited for scenarios where the goal is to learn a target function f:X→{0,1}f: X \to \{0,1\}, with XX representing the instance space of attribute-value pairs, and hypotheses h∈Hh \in H serving as approximations of ff. The core principle of version space learning involves representing the version space as the H′⊆HH' \subseteq H comprising all hypotheses in the predefined hypothesis space HH that correctly classify every training example. Positive examples (labeled 1) and negative examples (labeled 0) are used to eliminate hypotheses inconsistent with the observed data, progressively restricting H′H' while preserving all viable candidates. This elimination process ensures that the version space always contains the true target concept, assuming it is expressible within HH. Version space learning operates under key assumptions of a noise-free environment, where examples are accurately labeled, and a deterministic target that yields consistent classifications for any given instance. These principles enable exact representation of the version space, with the primary mechanism being the candidate elimination algorithm, which efficiently updates the set of consistent hypotheses as new examples arrive.

Role in Concept Learning

Version space learning occupies a foundational position within , a subfield of dedicated to inferring a target concept c—typically represented as a boolean-valued function—from a set of training examples consisting of positive instances (those belonging to c) and negative instances (those not belonging to c). This approach addresses the core challenge of inductive inference by systematically searching a predefined hypothesis space to identify all candidate concepts consistent with the observed , thereby enabling the learner to generalize to unseen instances without prior domain-specific knowledge beyond the hypothesis representation. A primary contribution of version space learning lies in its provision of an exact, complete representation of the set of all plausible that align with the examples, ensuring no potentially correct hypothesis is prematurely eliminated unless explicitly contradicted by new . This conservative strategy prevents overgeneralization, a common pitfall in inductive methods, and supports reliable by unanimous agreement among the remaining hypotheses when applied to data. Furthermore, it facilitates practical advancements in learning systems, such as the ability to detect inconsistencies in the data or to select informative examples that maximally reduce hypothesis . The method's is explicitly tied to the assumption that the target concept c is contained within the hypothesis H, which serves as the searchable of possible concepts; this bias allows for deductive justification of predictions but contrasts with purely statistical approaches by guaranteeing exactness in noise-free environments where sufficient examples are provided. In the of as a whole—a process of deriving general rules from finite, specific observations—version space learning exemplifies a logically rigorous framework that leverages partial orderings over hypotheses to refine the solution iteratively, laying groundwork for more scalable symbolic learning techniques.

Core Concepts

Hypothesis and Instance Spaces

In version space learning, the instance space XX refers to the complete set of all possible instances or examples that the learner might encounter, typically structured as attribute-value pairs describing properties of objects or events. For instance, in the EnjoySport domain, each instance x∈Xx \in X is a conjunction of discrete attribute values, such as (sunny, cloudy, rainy), air (warm, cold), (normal, high), (strong, weak), (warm, cool), and forecast (same, change), yielding a finite space of 3×2×2×2×2×2=963 \times 2 \times 2 \times 2 \times 2 \times 2 = 96 possible instances. The hypothesis space HH encompasses all conceivable hypotheses that map instances from XX to classifications, usually {0,1} indicating negative or positive examples relative to an unknown target concept c:X→{0,1}c: X \to \{0,1\}. in HH are commonly represented as conjunctions of constraints on the attributes, formalized as h(x)=⋀i=1nconstrainti(xi),h(x) = \bigwedge_{i=1}^n \text{constraint}_i(x_i), where each constrainti\text{constraint}_i can be a specific value (e.g., sky = sunny), a wildcard "?" (indicating "don't care," matching any value), or ⊥\perp (indicating impossibility, matching no value). This representation ensures HH is finite when XX is, and it must include the target concept cc. The space includes a maximally general hypothesis, often denoted as g0g_0 with all "?" wildcards, which classifies every instance as positive, and maximally specific hypotheses, such as those with ⊥\perp in positions that make them inconsistent except for exact matches. A key property of HH is its partial ordering by generality, where a hypothesis h1∈Hh_1 \in H is more general than h2∈Hh_2 \in H (denoted h2⪯gh1h_2 \preceq_g h_1) if, for every instance x∈Xx \in X, h1(x)=1h_1(x) = 1 whenever h2(x)=1h_2(x) = 1—meaning h1h_1 covers all positive instances covered by h2h_2 and possibly more. This ordering forms a lattice structure, with the maximally general hypothesis at the top and maximally specific ones at the bottom, enabling efficient search for consistent hypotheses during learning. The version space is the subset of HH consistent with observed training data, bounded by this partial order. Hypotheses are often encoded as vectors mirroring the instance attributes, such as ⟨?,[cold](/page/Cold),high,?,?,?⟩\langle ?, \text{[cold](/page/Cold)}, \text{high}, ?, ?, ?\rangle for a that requires air and high but ignores other attributes. This vector form facilitates under the generality ordering: h1⪯gh2h_1 \preceq_g h_2 if, for each attribute ii, the constraint in h1h_1 is at least as general as in h2h_2 (e.g., "?" is more general than a specific value, which is more general than ⊥\perp). Such properties ensure the space supports monotonic , where additional positive examples can only narrow the space without invalidating prior consistencies.

Version Space Boundaries

In version space learning, the version space VSVS represents the subset of hypotheses from the hypothesis space HH that are consistent with the observed training examples. Formally, VS={h∈H∣∀(x,c)∈D, h(x)=c}VS = \{ h \in H \mid \forall (x, c) \in D, \, h(x) = c \}, where DD is the set of training examples, each consisting of an instance xx and its cc (positive or negative). The hypotheses in VSVS are partially ordered by a generality relation, where a hypothesis h1h_1 is more general than h2h_2 (denoted h2⪯gh1h_2 \preceq_g h_1) if, for every instance x∈Xx \in X, h1(x)=1h_1(x) = 1 whenever h2(x)=1h_2(x) = 1—meaning h1h_1 covers all instances classified positively by h2h_2 and possibly more. The specific boundary SS of the version space consists of the maximally specific hypotheses within VSVS, which minimally cover all positive training examples while excluding all negative ones. These hypotheses represent the most restrictive consistent rules, ensuring no unnecessary generalizations that might include negatives. Initially, SS is empty before any positive examples are observed, or set to the first positive example upon its arrival, forming a single maximally specific hypothesis that matches only that instance. In contrast, the general boundary GG comprises the minimally general hypotheses in VSVS, which maximally cover positive examples without encompassing any negatives. These form the least restrictive consistent rules, often initialized as the set of all maximally general hypotheses in HH, such as the fully unconstrained hypothesis (?,?,…,?)(?, ?, \dots, ?) in conjunctive domains, which predicts positive for all instances until refined. Under the assumption that the hypothesis space HH is closed under and specialization—meaning for any two hypotheses, their least general and most specific specialization also exist in HH—the boundaries SS and GG provide a complete and compact representation of the entire VSVS. Specifically, any h∈VSh \in VS is more specific than or equal to at least one g∈Gg \in G and more general than or equal to at least one s∈Ss \in S, allowing efficient maintenance without enumerating all hypotheses in VSVS, which could be exponentially large. This boundary representation ensures that the version space can be queried or reduced scalably, supporting algorithms like candidate elimination for .

The Candidate Elimination Algorithm

Initialization and Example Processing

The Candidate Elimination algorithm begins with the initialization of two boundary sets that define the version space: the general boundary GG, which contains the maximally general hypotheses consistent with the training data, and the specific boundary SS, which contains the maximally specific hypotheses consistent with the data. Initially, G0G_0 is set to the singleton set containing the single most general hypothesis in the hypothesis space HH, typically represented as ⟨?,?,…,?⟩\langle ?, ?, \dots, ? \rangle for an attribute-value learning problem, where each "?" denotes an arbitrary value matcher that accepts any instance attribute. The initial specific boundary S0S_0 is set to the ∅\emptyset. Upon encountering the first positive training example (x,+)(x, +), the algorithm updates SS by setting it to the singleton set containing the description of xx itself, as this is the most specific consistent with the positive . Any hypotheses in G0G_0 inconsistent with this example—meaning they would incorrectly classify xx as negative—are removed. This initialization ensures the version space starts bounded by the extremes of HH and immediately incorporates the first confirming evidence, setting the stage for incremental refinement. The core of the algorithm is its incremental processing of subsequent training examples, which refines the version space without revisiting prior data. For each new example (x,c(x))(x, c(x)), where c(x)c(x) is the (positive or negative), the algorithm first removes from SS and GG any hypotheses inconsistent with (x,c(x))(x, c(x))—that is, hypotheses that do not correctly classify xx according to c(x)c(x). If c(x)c(x) is positive, the boundary SS is then minimally generalized using minimal generalizations with respect to xx to restore consistency; similarly, if c(x)c(x) is negative, the boundary GG is minimally specialized using minimal specializations with respect to xx (with details of these operations covered in boundary update rules). This process maintains the invariant that SS contains only maximally specific consistent hypotheses and GG contains only maximally general consistent ones, ensuring the version space VS={h∈H∣∀s∈S,s⪯h⪯∀g∈G}VS = \{ h \in H \mid \forall s \in S, s \preceq h \preceq \forall g \in G \} captures all viable candidates, where ⪯\preceq denotes the subsumption partial order. The overall procedure follows a straightforward loop over the training examples, as outlined in the high-level pseudocode below, assuming a noise-free dataset and that the target concept is representable in HH:

Initialize G to {most general hypothesis in H} Initialize S to ∅ Load training examples D For each example d in D: Remove from S any inconsistent with d Remove from G any inconsistent with d If d is positive: If S is now empty (as for the first positive example): Set S = {d} Else: Generalize S using minimal generalizations with respect to d, ensuring consistency with G Else: // d is negative Specialize G using minimal specializations with respect to d, ensuring consistency with S If S is empty or G is empty: Halt: Inconsistent training data (version space empty) If the boundaries S and G have converged (e.g., |S| = |G| and S = G): Halt: Version space converged to target concept Output VS or report inconsistency

Initialize G to {most general hypothesis in H} Initialize S to ∅ Load training examples D For each example d in D: Remove from S any inconsistent with d Remove from G any inconsistent with d If d is positive: If S is now empty (as for the first positive example): Set S = {d} Else: Generalize S using minimal generalizations with respect to d, ensuring consistency with G Else: // d is negative Specialize G using minimal specializations with respect to d, ensuring consistency with S If S is empty or G is empty: Halt: Inconsistent training data (version space empty) If the boundaries S and G have converged (e.g., |S| = |G| and S = G): Halt: Version space converged to target concept Output VS or report inconsistency

This structure loads the data once and processes examples sequentially, checking after each update whether the version space remains viable. Convergence occurs when the specific and general boundaries meet, specifically when every in GG subsumes every in SS and vice versa, often simplifying to S=GS = G in conjunctive hypothesis spaces, indicating has isolated the target concept. The process halts with inconsistency detection if, after processing an example, SS becomes empty (no specific fits all positives) or GG becomes empty (no general fits all negatives), or if no in SS is subsumed by any in GG (boundaries cross due to unrepresentable concepts or ). Under the assumptions of noise-free data and realizability, is guaranteed to converge to the correct version space after finitely many consistent examples.

Boundary Update Rules

In version space learning, the boundary update rules define how the specific boundary SS (maximally specific hypotheses) and general boundary GG (maximally general hypotheses) are adjusted to maintain consistency with new training examples, ensuring the version space VSVS contains only hypotheses hh that classify the examples correctly. For a positive example xx (classified as belonging to the target concept), the update proceeds as follows: each s∈Ss \in S that does not classify xx as positive is replaced by its minimal with respect to xx, denoted G(s,x)G(s, x), which is the least general subsuming both ss and xx; hypotheses in SS that already classify xx as positive remain unchanged. Additionally, any g∈Gg \in G that does not classify xx as positive is removed, as it is inconsistent with the example. If the new generalizations introduced to SS are not subsumed by existing members of SS, the boundary may be expanded with these minimal generalizations to preserve the maximally specific set. The consistency of a hypothesis hh with an example xx is checked via the classification function: h(x)h(x) is positive if and only if ⋀i(hi=xi∨hi=?)\bigwedge_i (h_i = x_i \lor h_i = ?), where attributes are indexed by ii and ?? denotes a wildcard matching any value. The generalization operator G(s,x)G(s, x) computes the least general generalization (LGG) component-wise: [G(s,x)]i=si[G(s, x)]_i = s_i if si=xis_i = x_i, otherwise ??. For a negative example xx (not belonging to the target concept), the update removes from SS any ss that classifies xx as positive, as such hypotheses are inconsistent and cannot be specialized further without violating prior positive examples. For each g∈Gg \in G that classifies xx as positive, it is replaced by a set of minimal specializations S(g,x)S(g, x), which are the least specific hypotheses more specific than gg that exclude xx; these are typically generated by varying one attribute differing from xx to a value that excludes it (e.g., using near-miss heuristics to restrict the attribute to not match xix_i), while ensuring the specializations subsume at least one s∈Ss \in S to avoid inconsistency. Specialization can be formalized via set difference or attribute restriction: for instance, S(g,x)S(g, x) includes hypotheses where one attribute ii (where gi=?g_i = ? or gi≠xig_i \neq x_i) is set to a value excluding xix_i, minimizing the increase in specificity. The overall version space maintenance follows the recursive formulation VSn+1={h∈VSn∣h(xn+1)=cn+1}VS_{n+1} = \{ h \in VS_n \mid h(x_{n+1}) = c_{n+1} \}, where cn+1c_{n+1} is the correct of the new example xn+1x_{n+1}; this is efficiently represented and updated using the SS and GG boundaries without enumerating all hypotheses in VSVS.

Illustrative Examples

Enjoy Sport Domain

The Enjoy Sport domain serves as a foundational example in , where the task is to determine whether a person enjoys their favorite water sport on a given day based on environmental conditions. The instance space XX consists of all possible days described by six discrete attributes: (taking values sunny, cloudy, or rainy), AirTemp (warm or cold), (normal or high), Wind (strong or weak), Water (warm or cool), and Forecast (same or change). This results in a total of 96 possible instances, as the attributes have 3, 2, 2, 2, 2, and 2 values respectively. Hypotheses in this domain are represented as conjunctions of constraints over these attributes, denoted as h=⟨v1,v2,…,v6⟩h = \langle v_1, v_2, \dots, v_6 \rangle, where each viv_i is either a specific attribute value (e.g., sunny for Sky), "?" (matching any value for that attribute), or ∅\emptyset (matching no value, effectively excluding instances). Positive training examples are those days where the is enjoyed (labeled Yes), while negative examples are those where it is not (labeled No). For instance, the training instance ⟨\langlesunny, warm, normal, strong, warm, same⟩\rangle is positive, indicating enjoyment under these conditions, whereas ⟨\langlerainy, cold, high, strong, warm, change⟩\rangle is negative. This domain illustrates the applicability of version space learning by providing a simple, relatable scenario for exploring conjunctive hypotheses and attribute-based constraints, where the goal is to identify conditions consistent with the observed training data without requiring complex computations.

Step-by-Step Boundary Evolution

The candidate elimination algorithm begins with the version space initialized by a single maximally general hypothesis in the general boundary set GG, represented as G={⟨?,?,?,?,?,?⟩}G = \{ \langle ?, ?, ?, ?, ?, ? \rangle \}, where each "?" denotes any possible value for the corresponding attribute (Sky, AirTemp, Humidity, Wind, Water, Forecast). The specific boundary set SS starts with a single maximally specific hypothesis, S={⟨∅,∅,∅,∅,∅,∅⟩}S = \{ \langle \emptyset, \emptyset, \emptyset, \emptyset, \emptyset, \emptyset \rangle \}, indicating no constraints initially. Processing the first positive training example—Sunny, Warm, Normal, Strong, Warm, Same—the algorithm replaces the initial specific with this instance, yielding S={⟨Sunny,Warm,Normal,Strong,Warm,Same⟩}S = \{ \langle \text{Sunny}, \text{Warm}, \text{Normal}, \text{Strong}, \text{Warm}, \text{Same} \rangle \}, as it is the only consistent specific hypothesis. The general boundary remains unchanged, since the example is consistent with the maximally general . For the second positive example—Sunny, Warm, High, Strong, Warm, Same—the specific boundary generalizes by replacing the differing attribute (Humidity: Normal to High) with "?", resulting in S={⟨Sunny,Warm,?,Strong,Warm,Same⟩}S = \{ \langle \text{Sunny}, \text{Warm}, ?, \text{Strong}, \text{Warm}, \text{Same} \rangle \}. Again, GG stays as {⟨?,?,?,?,?,?⟩}\{ \langle ?, ?, ?, ?, ?, ? \rangle \}, fully consistent with the example. The third example, a negative instance—Rainy, Cold, High, Strong, Warm, Change—leaves SS unchanged, as it does not match the specific hypothesis and thus imposes no generalization. However, GG specializes by eliminating the maximally general hypothesis and replacing it with minimally general ones that exclude this negative example, such as by restricting Sky to not Rainy, AirTemp to not Cold, and Forecast to not Change; this yields G={⟨Sunny,?,?,?,?,?⟩,⟨?,Warm,?,?,?,?⟩,⟨?,?,?,?,?,Same⟩}G = \{ \langle \text{Sunny}, ?, ?, ?, ?, ? \rangle, \langle ?, \text{Warm}, ?, ?, ?, ? \rangle, \langle ?, ?, ?, ?, ?, \text{Same} \rangle \}. Finally, the fourth positive example—Sunny, Warm, High, Strong, Cool, Change—generalizes SS further by replacing Water (Warm to Cool) and Forecast (Same to Change) with "?", producing S={⟨Sunny,Warm,?,Strong,?,?⟩}S = \{ \langle \text{Sunny}, \text{Warm}, ?, \text{Strong}, ?, ? \rangle \}. For GG, inconsistent hypotheses (e.g., the one restricting Forecast to Same) are removed, leaving G={⟨Sunny,?,?,?,?,?⟩,⟨?,Warm,?,?,?,?⟩}G = \{ \langle \text{Sunny}, ?, ?, ?, ?, ? \rangle, \langle ?, \text{Warm}, ?, ?, ?, ? \rangle \}. These boundaries represent all hypotheses consistent with the full training dataset. The evolution of the boundaries is illustrated in the following table, showing the state after each example and the key updates that eliminate inconsistent hypotheses:
After ExampleSpecific Boundary SSGeneral Boundary GGKey Update
Initialization{⟨∅,∅,∅,∅,∅,∅⟩}\{\langle \emptyset, \emptyset, \emptyset, \emptyset, \emptyset, \emptyset \rangle\}{⟨?,?,?,?,?,?⟩}\{\langle ?, ?, ?, ?, ?, ? \rangle\}N/A
1 (Positive: Sunny, Warm, Normal, Strong, Warm, Same){⟨Sunny,Warm,Normal,Strong,Warm,Same⟩}\{\langle \text{Sunny}, \text{Warm}, \text{Normal}, \text{Strong}, \text{Warm}, \text{Same} \rangle\}{⟨?,?,?,?,?,?⟩}\{\langle ?, ?, ?, ?, ?, ? \rangle\}Replace initial SS with the example; no change to GG.
2 (Positive: Sunny, Warm, High, Strong, Warm, Same){⟨Sunny,Warm,?,Strong,Warm,Same⟩}\{\langle \text{Sunny}, \text{Warm}, ?, \text{Strong}, \text{Warm}, \text{Same} \rangle\}{⟨?,?,?,?,?,?⟩}\{\langle ?, ?, ?, ?, ?, ? \rangle\}Generalize Humidity in SS to "?"; no change to GG.
3 (Negative: Rainy, Cold, High, Strong, Warm, Change){⟨Sunny,Warm,?,Strong,Warm,Same⟩}\{\langle \text{Sunny}, \text{Warm}, ?, \text{Strong}, \text{Warm}, \text{Same} \rangle\}{⟨Sunny,?,?,?,?,?⟩,⟨?,Warm,?,?,?,?⟩,⟨?,?,?,?,?,Same⟩}\{\langle \text{Sunny}, ?, ?, ?, ?, ? \rangle, \langle ?, \text{Warm}, ?, ?, ?, ? \rangle, \langle ?, ?, ?, ?, ?, \text{Same} \rangle\}No change to SS; specialize GG by adding minimal restrictions to exclude the negative.
4 (Positive: Sunny, Warm, High, Strong, Cool, Change){⟨Sunny,Warm,?,Strong,?,?⟩}\{\langle \text{Sunny}, \text{Warm}, ?, \text{Strong}, ?, ? \rangle\}{⟨Sunny,?,?,?,?,?⟩,⟨?,Warm,?,?,?,?⟩}\{\langle \text{Sunny}, ?, ?, ?, ?, ? \rangle, \langle ?, \text{Warm}, ?, ?, ?, ? \rangle\}Generalize Water and Forecast in SS to "?"; remove inconsistent hypothesis from GG.

Historical Development

Origins in Symbolic AI

Version space learning emerged within the symbolic AI paradigm during the late , as part of broader efforts in inductive learning and knowledge representation. Early systems such as META-DENDRAL, developed in the , exemplified this direction by using data to infer production rules for molecular structures, marking an initial foray into automated rule discovery from . This work reflected the era's focus on heuristic programming to simulate scientific reasoning, where knowledge was represented symbolically through logical structures rather than numerical approximations. The approach was part of a transitional shift in AI from purely rule-based expert systems, which relied on manually encoded knowledge, to data-driven inductive methods that could generalize from examples. In symbolic AI, this evolution emphasized discrete, logical representations of concepts, contrasting with later statistical paradigms, and addressed the need for machines to acquire incrementally without exhaustive programming. Tom Mitchell played a pivotal role in formalizing version space learning as a framework for exactly solvable problems in symbolic AI, prioritizing logical to maintain consistency with observed data over probabilistic approximations. This framework built on prior ideas, including Gordon Plotkin's concept of least general (LGG) from , which provided a method for finding the most specific unifying hypothesis from examples, and Patrick Winston's 1970 ARCH learning program, which demonstrated structural concept acquisition in a by refining hypotheses based on positive and negative instances to handle uncertainty in hypothesis selection. Mitchell's 1982 work further refined the approach by framing as a in the hypothesis space, systematically narrowing the space of plausible through and specialization. This emphasized exact solvability under noise-free assumptions, aligning with symbolic AI's goal of transparent, logically sound induction. The candidate elimination algorithm, introduced in Mitchell's 1977 work, operationalized these ideas and remained rooted in the era's symbolic foundations.

Key Publications and Extensions

The foundational work on version space learning was introduced by in his 1977 paper "Version Spaces: A Candidate Elimination Approach to Rule Learning," presented at the International Joint Conference on (IJCAI-77, pp. 305-310), where he defined the version space as the set of all hypotheses consistent with training examples and proposed the candidate elimination algorithm to efficiently maintain it. This was further formalized in his 1982 paper "Generalization as Search," published in the Artificial Intelligence journal (Volume 18, Issue 2, pp. 203-226). Early implementations focused on practical systems and efficiency enhancements, such as Sverdlik and Reynolds' 1992 paper "Dynamic Version Spaces in Machine Learning," presented at the Fourth International Conference on Tools with Artificial Intelligence (pp. 308-315), which developed a hybrid algorithm integrating version spaces with cultural algorithms to handle concepts with multiple disjuncts in dynamic environments. Similarly, Hong and Tsang's 1997 paper "A Generalized Version Space Learning Algorithm for Noisy and Uncertain Data," in IEEE Transactions on Knowledge and Data Engineering (Volume 9, Issue 2, pp. 336-340), extended the framework to improve efficiency by incorporating probabilistic handling of noise and uncertainty, allowing the algorithm to maintain a bounded version space under imperfect data conditions. An important extension addressing noise and inconsistency came from Dubois and Quafafou in their 2002 chapter "Concept Learning with Approximation: Rough Version Spaces," in the Lecture Notes in Computer Science (Volume 2475, pp. 239-246), which integrated rough set theory to define approximate boundaries in the version space, enabling learning from inconsistent examples by distinguishing certain, possible, and boundary regions of hypotheses. Version space learning has since been established as a standard example in machine learning, as detailed by Russell and Norvig in their 2003 textbook Artificial Intelligence: A Modern Approach (2nd Edition, , pp. 683-686), where it is presented as a foundational method for from examples within the broader context of inductive inference.

Applications and Limitations

Practical Uses in Machine Learning

Version space learning has been employed in early expert systems for , enabling the induction of rules from training examples to support in specialized domains. A seminal application is its integration into the Meta-DENDRAL program, where it serves as a component for learning production rules to interpret chemical mass spectra, addressing the knowledge acquisition bottleneck by systematically refining hypotheses consistent with observed data. This approach exemplifies its utility in diagnostic expert systems, where it facilitates rule learning from examples in structured, symbolic environments such as chemical analysis. In terms of implementations, version space learning has been incorporated into variants of rule-learning algorithms like AQ, developed by Ryszard Michalski, which share conceptual similarities in covering positive examples while generalizing from data. It also aligns with (ILP) systems, where the maintenance of a space bounded by consistent rules mirrors version space principles to derive logical programs from examples and background . Practically, it proves effective in small, discrete attribute spaces, as demonstrated in fault for power distribution networks; here, a version space-based diagnostician learns diagnostic rules automatically from system data, using user-provided background to overcome manual encoding limitations and achieve reliable fault identification in simulated environments. Theoretically, version space learning acts as a benchmark for exact within the Probably Approximately Correct (PAC) framework, where the size of the version space provides finite sample complexity bounds: with sufficient examples, the probability of identifying a with at most ε is at least 1-δ, assuming a finite hypothesis space. In comparisons to other methods, it contrasts with decision tree learners like , which output a single by greedily selecting features; version space instead preserves the full set of consistent hypotheses, enabling a more exhaustive exploration of plausible concepts without premature commitment. In contemporary , version space learning occupies a niche in explainable AI (XAI), particularly for settings where generating the complete set of interpretable hypotheses—rather than a black-box model—facilitates understanding and trust in predictions. This explicit enumeration of boundary sets supports transparent in domains requiring , such as regulatory-compliant systems, by highlighting the range of rules compatible with the data.

Challenges and Modern Adaptations

One major challenge in version space learning is its sensitivity to noisy or inconsistent data, where even a single erroneous example can prune viable hypotheses from the version space, leading to premature boundary collapse and potential elimination of the true target concept. This issue arises because the candidate-elimination algorithm strictly enforces consistency, removing any hypothesis that conflicts with training examples, which exacerbates problems in real-world datasets containing measurement errors or outliers. Version space learning also faces computational limitations when dealing with large hypothesis spaces, as the exponential growth in the number of possible hypotheses requires efficient representation and maintenance of the general and specific boundaries, which becomes intractable without specialized data structures. Furthermore, the method assumes hypotheses are conjunctive, restricting it to learning simple, single-clause concepts and struggling with disjunctive or more complex logical structures that demand broader representational power. issues extend to continuous attributes, where defining precise boundaries for ranges demands additional mechanisms, such as interval generalizations, to avoid infinite hypothesis . To address noise tolerance, the Rough Version Space approach, introduced in 2002, integrates rough set theory by employing lower and upper approximations to maintain a flexible version space that accommodates uncertain or inconsistent examples without full collapse. Similarly, version space algebra, proposed in 2000, extends the framework to compose version spaces for learning complex functions in programming by demonstration, enabling the handling of multi-step tasks through algebraic operations on hypothesis sets. In contemporary , version space learning is less prevalent compared to neural networks or ensemble methods like random forests, primarily due to its constraints on high-dimensional or large-scale , where the latter excel in empirical performance without explicit hypothesis maintenance. However, it retains relevance in hybrid symbolic-neural systems, where its interpretable hypothesis versioning supports explainability in neural architectures, bridging gaps in deep learning's black-box nature.
Add your contribution
Related Hubs
User Avatar
No comments yet.