Recent from talks
Nothing was collected or created yet.
Adaptive Huffman coding
View on WikipediaAdaptive Huffman coding (also called Dynamic Huffman coding) is an adaptive coding technique based on Huffman coding. It permits building the code as the symbols are being transmitted, having no initial knowledge of source distribution, that allows one-pass encoding and adaptation to changing conditions in data.[1]
The benefit of one-pass procedure is that the source can be encoded in real time, though it becomes more sensitive to transmission errors, since just a single loss ruins the whole code, requiring error detection and correction.
Algorithms
[edit]There are a number of implementations of this method, the most notable are FGK (Faller-Gallager-Knuth) and Vitter algorithm.
FGK Algorithm
[edit]It is an online coding technique based on Huffman coding. Having no initial knowledge of occurrence frequencies, it permits dynamically adjusting the Huffman's tree as data are being transmitted. In a FGK Huffman tree, a special external node, called 0-node, is used to identify a newly coming character. That is, whenever new data is encountered, output the path to the 0-node followed by the data. For a past-coming character, just output the path of the data in the current Huffman's tree. Most importantly, we have to adjust the FGK Huffman tree if necessary, and finally update the frequency of related nodes. As the frequency of a datum is increased, the sibling property of the Huffman's tree may be broken. The adjustment is triggered for this reason. It is accomplished by consecutive swappings of nodes, subtrees, or both. The data node is swapped with the highest-ordered node of the same frequency in the Huffman's tree, (or the subtree rooted at the highest-ordered node). All ancestor nodes of the node should also be processed in the same manner.
Since the FGK Algorithm has some drawbacks about the node-or-subtree swapping, Vitter proposed another algorithm to improve it.
Vitter algorithm
[edit]Some important terminologies & constraints :-
- Implicit Numbering : It simply means that nodes are numbered in increasing order by level and from left to right. i.e. nodes at bottom level will have low implicit number as compared to upper level nodes and nodes on same level are numbered in increasing order from left to right. In other terms, when we have built the Huffman tree, when merging two nodes into a parent node, we have set the one with the lower value as the left child, and the one with the higher value as the right child.
- Invariant : For each weight w, all leaves of weight w precede all internal nodes having weight w. In other terms, when we have built the Huffman tree, if several nodes had the same value, we prioritized merging the leaves over the internal nodes.
- Blocks : Nodes of same weight and same type (i.e. either leaf node or internal node) form a Block.
- Leader : Highest numbered node in a block.
Blocks are interlinked by increasing order of their weights.
A leaf block always precedes internal block of same weight, thus maintaining the invariant.
NYT (Not Yet Transferred) is a special node used to represent symbols which are 'not yet transferred'.








algorithm for adding a symbol is
leaf_to_increment := NULL
p := pointer to the leaf node containing the next symbol
if (p is NYT) then
Extend p by adding two children
Left child becomes new NYT and right child is the new symbol leaf node
p := parent of new symbol leaf node
leaf_to_increment := Right Child of p
else
Swap p with leader of its block
if (new p is sibling to NYT) then
leaf_to_increment := p
p := parent of p
while (p ≠ NULL) do
Slide_And_Increment(p)
if (leaf_to_increment != NULL) then
Slide_And_Increment(leaf_to_increment)
function Slide_And_Increment(p) is
previous_p := parent of p
if (p is an internal node) then
Slide p in the tree higher than the leaf nodes of weight wt + 1
increase weight of p by 1
p := previous_p
else
Slide p in the tree higher than the internal nodes of weight wt
increase weight of p by 1
p := new parent of p.
Encoder and decoder start with only the root node, which has the maximum number. In the beginning it is our initial NYT node.
When we transmit an NYT symbol, we have to transmit code for the NYT node, then for its generic code.
For every symbol that is already in the tree, we only have to transmit code for its leaf node.
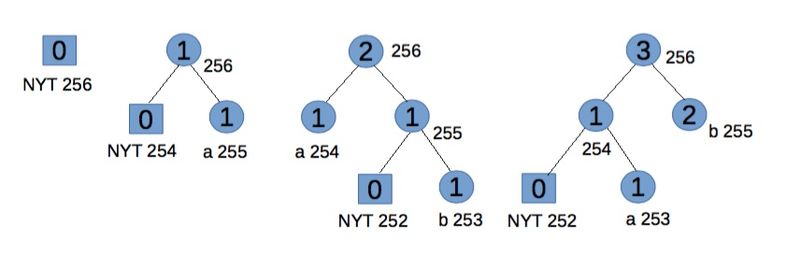
Example
[edit]Encoding "abb" gives 01100001 001100010 11.
Step 1:
Start with an empty tree.
For "a" transmit its binary code.
Step 2:
NYT spawns two child nodes: 254 and 255, both with weight 0. Increase weight for root and 255. Code for "a", associated with node 255, is 1.
For "b" transmit 0 (for NYT node) then its binary code.
Step 3:
NYT spawns two child nodes: 252 for NYT and 253 for leaf node, both with weight 0. Increase weights for 253, 254, and root. To maintain Vitter's invariant that all leaves of weight w precede (in the implicit numbering) all internal nodes of weight w, the branch starting with node 254 should be swapped (in terms of symbols and weights, but not number ordering) with node 255. Code for "b" is 11.
For the second "b" transmit 11.
For the convenience of explanation this step doesn't exactly follow Vitter's algorithm,[2] but the effects are equivalent.
Step 4:
Go to leaf node 253. Notice we have two blocks with weight 1. Node 253 and 254 is one block (consisting of leaves), node 255 is another block (consisting of internal nodes). For node 253, the biggest number in its block is 254, so swap the weights and symbols of nodes 253 and 254. Now node 254 and the branch starting from node 255 satisfy the SlideAndIncrement condition[2] and hence must be swapped. At last increase node 255 and 256's weight.
Future code for "b" is 1, and for "a" is now 01, which reflects their frequency.
References
[edit]- ^ Ze-Nian Li; Mark S. Drew; Jiangchuan Liu (9 April 2014). Fundamentals of Multimedia. Springer Science & Business Media. ISBN 978-3-319-05290-8.
- ^ a b "Adaptive Huffman Coding". Cs.duke.edu. Retrieved 2012-02-26.
- Vitter's original paper: J. S. Vitter, "Design and Analysis of Dynamic Huffman Codes", Journal of the ACM, 34(4), October 1987, pp 825–845.
- J. S. Vitter, "ALGORITHM 673 Dynamic Huffman Coding", ACM Transactions on Mathematical Software, 15(2), June 1989, pp 158–167. Also appears in Collected Algorithms of ACM.
- Donald E. Knuth, "Dynamic Huffman Coding", Journal of Algorithm, 6(2), 1985, pp 163–180.
External links
[edit] This article incorporates public domain material from Paul E. Black. "adaptive Huffman coding". Dictionary of Algorithms and Data Structures. NIST.
This article incorporates public domain material from Paul E. Black. "adaptive Huffman coding". Dictionary of Algorithms and Data Structures. NIST.- University of California Dan Hirschberg site
- Cardiff University Dr. David Marshall site
- C implementation of Vitter algorithm
- Excellent description from Duke University
Adaptive Huffman coding
View on GrokipediaFundamentals
Huffman Coding Basics
Huffman coding is an algorithm for lossless data compression that generates prefix-free variable-length codes for symbols based on their frequencies in the source data, thereby minimizing the average number of bits required per symbol and approaching the entropy limit of the source. Developed by David A. Huffman in 1952, it constructs codes such that more frequent symbols receive shorter binary codes, while less frequent ones get longer codes, ensuring no code is a prefix of another to allow unambiguous decoding.[6] This approach enables entropy coding, where the expected code length is close to the Shannon entropy of the source distribution. The construction of a static Huffman tree begins with the frequencies of each symbol in a fixed alphabet, treating them as leaf nodes with those weights. The algorithm iteratively combines the two nodes with the lowest frequencies into a new internal node whose frequency is the sum of its children, repeating until a single root node remains, forming a full binary tree. Codes are then assigned by traversing from the root to each leaf, using 0 for left branches and 1 for right branches, resulting in shorter paths (and thus codes) for higher-frequency symbols.[6] This bottom-up merging ensures the resulting code is optimal among prefix codes for the given frequencies, as proven by the minimum-redundancy property of the tree.[6] The theoretical foundation for code lengths derives from information theory: the ideal code length for a symbol with probability satisfies , where the average length is at least the entropy . Huffman coding achieves this bound within 1 bit per symbol on average for prefix codes. For example, consider an alphabet with symbols A (frequency 5), B (2), C (1), and D (1); the tree construction yields codes A: 0, B: 10, C: 110, D: 111, with average length bits per symbol.[7] Static Huffman coding is optimal for sources with known, stationary probability distributions, providing the shortest possible average code length among instantaneous codes.[6] It forms a core component in numerous compression standards, including JPEG for image data and MPEG for video, due to its efficiency and simplicity when frequencies can be precomputed.[8] Adaptive variants extend this framework to handle unknown or evolving distributions without requiring prior frequency knowledge.[6]Motivation for Adaptive Coding
Static Huffman coding, while optimal for sources with fixed and known symbol probabilities, imposes significant limitations in practical applications. It requires a complete scan of the input data to compute frequency counts before constructing the coding tree, resulting in a two-pass encoding process that doubles the computational overhead and delays compression until the entire dataset is available.[2] This approach proves ineffective for non-stationary sources, where symbol probabilities vary over time, or for streaming data scenarios, as the static tree cannot adapt to evolving statistics without rebuilding, leading to suboptimal compression ratios.[2] Adaptive coding addresses these constraints by enabling dynamic tree updates during a single encoding pass, making it essential for real-time applications such as live data transmission in telecommunications or sensor networks. It is particularly suited to scenarios with unknown initial symbol distributions, such as compressing files with unpredictable content, or handling changing data statistics, for example, in natural language processing where word frequencies shift across document sections or evolving contexts.[2] Early foundations in information theory, including Shannon's entropy measures for sources with time-varying probabilities, underscored the need for methods that track and respond to statistical shifts without prior knowledge. The concept of adaptive Huffman coding emerged to facilitate one-pass compression, conceived independently by Newton Faller in 1973, who introduced an adaptive system capable of updating codes on-the-fly based on observed symbols, and by Robert G. Gallager in 1978, who explored algorithmic variations for adapting to slowly varying source estimates.[9][10] These innovations allow encoding without predefined statistics, incrementally refining the Huffman tree as symbols arrive, which supports efficient online processing and often yields better performance than static methods for dynamic data by reducing overhead and improving adaptability.[2]Core Principles
Not-Yet-Transmitted Node
In adaptive Huffman coding, the Not-Yet-Transmitted (NYT) node serves as a special leaf node that represents all symbols from the source alphabet which have not yet appeared in the input stream.[2] This node, sometimes referred to as the 0-node, is essential for handling an initially unknown or partially known alphabet without requiring a static code table built in advance.[2] It is typically assigned a special identifier outside the symbol range, such as 0 (the 0-node), to distinguish it from actual symbols in implementations assuming a fixed maximum alphabet size. The Huffman tree begins with this single NYT node as both the root and sole leaf, assigned an initial codeword of '0' in a binary tree configuration.[2] Its weight is set to 0, reflecting the absence of transmitted symbols at the start.[11] When the first symbol arrives for encoding, the path to the NYT node provides its provisional code, which is transmitted to the decoder, signaling an unseen symbol.[12] This is followed by the actual symbol value, often encoded in a fixed-length format to identify it uniquely among potential unused symbols.[2] Upon transmission, the NYT node is replaced and split to incorporate the new symbol while preserving the tree's structure.[5] Specifically, the original NYT becomes an internal node, from which two new sibling leaves branch: one leaf dedicated to the newly introduced symbol (with an initial weight of 1), and the other serving as the updated NYT node (retaining weight 0) for future unseen symbols.[2] This sibling pairing maintains the Huffman tree's validity by ensuring that combined node weights adhere to the sibling property, where siblings represent the lowest-weight combinations at each level.[5] The NYT mechanism enables true one-pass encoding and decoding, allowing the tree to grow incrementally as the input stream reveals the effective alphabet without prior statistical knowledge or multiple traversals of the data.[2] This innovation, central to the Faller-Gallager-Knuth (FGK) approach, ensures prefix-free codes remain optimal as symbols are introduced.Tree Update Mechanisms
In adaptive Huffman coding, the sibling property ensures that the coding tree remains nearly optimal by requiring that all leaves and internal nodes with the same weight are siblings, and the nodes are ordered in nondecreasing weight such that nodes and share a common parent for , where is the number of leaves.[1] This property, equivalent to the tree being a valid Huffman tree, allows for efficient prefix codes while adapting to changing symbol frequencies without full recomputation.[1] The update process begins after encoding a symbol using the FGK two-phase procedure to maintain the sibling property. In Phase 1, each node along the path from the leaf to the root is interchanged with the highest-numbered node of equal weight in the relevant subtree or the entire tree.[13] In Phase 2, the weight of the leaf node is incremented by 1, and this increment is propagated upward to all ancestor nodes by adding 1 to each.[13] These interchanges and increments ensure the tree reflects the updated frequencies while preserving the ordering and property.[1] To balance efficiency and optimality, adaptive Huffman coding employs partial updates through these incremental interchanges and increments rather than rebuilding the entire tree from scratch after each symbol.[1] Partial updates limit operations to the depth of the affected node, typically time where is the code length, avoiding the higher cost of full rebuilds that would require time for symbols.[1] For new symbols, the Not-Yet-Transmitted (NYT) node facilitates introduction without disrupting existing updates.[1] A key limitation of these mechanisms is their sensitivity to transmission errors, as a single bit error can corrupt the shared tree state between encoder and decoder, leading to desynchronization and incorrect subsequent decodings.[14] Such corruption propagates through the stream, potentially invalidating all remaining data until resynchronization, which necessitates additional error-correcting codes or periodic tree resets to maintain reliability.[15]Algorithms
FGK Algorithm
The FGK algorithm, also known as the Faller-Gallager-Knuth algorithm, is the original method for implementing adaptive Huffman coding in a single pass over the data stream. It was first proposed independently by Newton Faller in 1973 and Robert G. Gallager in 1978, with Donald E. Knuth providing significant refinements in 1985 to enable efficient dynamic tree maintenance.[5] The algorithm employs a binary tree structure where leaves represent symbols from the input alphabet, and the weight of each node is the sum of its descendant leaves' frequencies. Initially, the tree consists solely of a special external node called the 0-node, which represents all unseen symbols. As symbols are encountered, leaves are added explicitly, with nodes numbered sequentially: leaves receive numbers starting from 1 in the order of their first appearance, while internal nodes are assigned higher numbers up to the total node count. This explicit numbering facilitates traversal and updates while ensuring siblings remain adjacent in the tree representation.[5] To encode a symbol, the algorithm traverses from the root to the corresponding leaf (or the 0-node for unseen symbols), outputting the path as a binary codeword. For a newly encountered symbol, after transmitting the 0-node's code, a fixed-length identifier—typically the binary encoding of the symbol's sequential appearance index among unseen symbols—is appended to specify its identity. The 0-node is then replaced by creating a new internal node with two children: a leaf for the new symbol (with initial weight 1) and a successor 0-node (with weight equal to the number of remaining unseen symbols).[5][2] Following encoding, the weight of the relevant leaf is incremented by 1, and internal node weights along the path are updated accordingly. To approximate Huffman optimality without full tree reconstruction, the algorithm enforces Gallager's sibling property, which requires that for every pair of sibling nodes, the higher-numbered sibling has a weight at least as large as the lower-numbered one. This is achieved through a series of pairwise swaps: starting from the incremented leaf, if it violates the property with its sibling, they are swapped; the process repeats upward toward the root until no further violations occur. Knuth's primary contribution was an optimized procedure for detecting these violations via direct weight comparisons between siblings and parents, ensuring the update completes in O(l) time, where l is the length of the codeword for the symbol.[5] As the first practical one-pass adaptive Huffman coder, FGK enables real-time compression without prior knowledge of symbol frequencies. However, its reliance on potentially numerous swaps per update introduces overhead, rendering it less efficient than later refinements in terms of average computational cost.[16]Vitter Algorithm
The Vitter algorithm, developed by Jeffrey Scott Vitter in his 1987 paper published in the Journal of the ACM, builds upon the FGK algorithm to construct dynamic Huffman codes in a single pass while significantly reducing the computational overhead of tree updates during encoding and decoding.[16] This improvement addresses the inefficiencies in FGK's explicit node management, enabling more practical real-time applications by optimizing the data structure and update procedures.[16] A central innovation is the use of implicit node numbering, where nodes are ordered by their depth in the tree, with leaves positioned before internal nodes of the same weight; this scheme avoids costly interchanges between node types during updates.[16] To maintain the tree's structure efficiently, Vitter introduces two invariants: first, that leaves always precede internal nodes sharing the same weight; second, that the numbering minimizes both the sum of node indices weighted by their depths (Σ_j h_j) and the maximum such weighted depth (max_j h_j).[16] These invariants ensure the tree remains balanced and ordered without frequent renumbering. The core update mechanism is the Slide_And_Increment function, which relocates a selected node by sliding it rightward through its current block until it reaches an appropriate position based on the new weight, then increments the weight; leaves are handled by dynamically creating new parent nodes as needed, while internal nodes require pointer adjustments to preserve sibling relationships.[16] To facilitate rapid node location, the algorithm organizes the tree into blocks grouped by weight classes, with separate blocks for leaves and internal nodes that are linked in order of increasing weight, allowing updates to traverse only relevant sections rather than the entire structure.[16] Overall, these enhancements achieve an average update time of O(log n), where n is the number of nodes, outperforming FGK's potential worst-case scenarios and making the algorithm suitable for implementation in resource-constrained environments.[16] Vitter's approach is embodied in reference implementations, such as Algorithm 673 published in ACM Transactions on Mathematical Software, which provides a Pascal-based realization of the method for practical use.Examples
Encoding Process Illustration
To illustrate the encoding process in the Vitter algorithm for adaptive Huffman coding, consider encoding the short sequence "abb" over an 8-bit alphabet (256 possible symbols), starting with an empty tree consisting solely of a single Not-Yet-Transmitted (NYT) node with weight 0.[1][17] Initial Tree:The tree is a single leaf node representing the NYT, with no symbols yet transmitted. Its codeword is the empty path from the root (implicitly the node itself). For the first symbol 'a' (ASCII 97), which is not yet in the tree: Transmit the empty codeword for the NYT, followed immediately by the 8-bit binary representation of 'a' ("01100001"). Then, split the NYT node: Create a new internal node from the old NYT (weight 1), attach a new NYT leaf (weight 0) as its left child (code 0) and a leaf for 'a' (weight 1, code 1) as its right child. The updated tree now reflects the new structure.[1][17]
Initial (before 'a'):
NYT (wt=0)
After 'a' (split and increment):
Root (wt=1)
/ \
NYT (wt=0, code: 0) 'a' (wt=1, code: 1)
Initial (before 'a'):
NYT (wt=0)
After 'a' (split and increment):
Root (wt=1)
/ \
NYT (wt=0, code: 0) 'a' (wt=1, code: 1)
After 'b' (split, introduce, and update):
Root (wt=2)
/ \
Internal (wt=1) 'a' (wt=1, code: 1)
/ \
NYT (wt=0, code: 00) 'b' (wt=1, code: 01)
After 'b' (split, introduce, and update):
Root (wt=2)
/ \
Internal (wt=1) 'a' (wt=1, code: 1)
/ \
NYT (wt=0, code: 00) 'b' (wt=1, code: 01)
After second 'b' (increment and slide with swap):
Root (wt=3)
/ \
'a' (wt=1, code: 0) Internal (wt=2)
/ \
NYT (wt=0, code: 10) 'b' (wt=2, code: 11)
After second 'b' (increment and slide with swap):
Root (wt=3)
/ \
'a' (wt=1, code: 0) Internal (wt=2)
/ \
NYT (wt=0, code: 10) 'b' (wt=2, code: 11)
Implementation Pseudocode
Adaptive Huffman coding implementations typically represent the Huffman tree using an array of nodes, each containing fields such as left child index, right child index, parent index, and weight, facilitating efficient traversal and updates in languages like C++ or Python.[19]Tree Initialization
The tree begins with a single root node that is also the Not-Yet-Transmitted (NYT) leaf, representing no symbols seen yet. Symbols are identified by their 8-bit values. Internal nodes are allocated as needed during updates. Pseudocode for initialization (based on FGK algorithm, adaptable to Vitter):procedure InitializeTree()
root = createNode() // NYT node with weight 0
root.left = null
root.right = null
root.parent = null
root.weight = 0
root.symbol = -1 // No symbol
nodeCount = 1
// Allocate array of sufficient size for nodes (e.g., 2*257 - 1 for 256 symbols)
procedure InitializeTree()
root = createNode() // NYT node with weight 0
root.left = null
root.right = null
root.parent = null
root.weight = 0
root.symbol = -1 // No symbol
nodeCount = 1
// Allocate array of sufficient size for nodes (e.g., 2*257 - 1 for 256 symbols)
Encoding Function
Encoding traverses the tree from root to the leaf corresponding to the symbol, outputting the path bits (0 for left, 1 for right). For unseen symbols, the NYT path is output followed by the symbol's 8-bit representation, then the NYT is split to introduce the new symbol. Pseudocode for encoding (Vitter/FGK-style, for 8-bit alphabet):procedure Encode(symbol, tree, bitstream)
if symbol is in tree:
current = root
code = empty bit string
while current is not leaf:
if symbol is in left subtree:
append 0 to code
current = current.left
else:
append 1 to code
current = current.right
output code to bitstream
leaf = current // For update
else: // New symbol
current = root
code = empty bit string
nytNode = findNYT(tree) // Locate current NYT leaf
while current != nytNode:
if nytNode is in left subtree of current:
append 0 to code
current = current.left
else:
append 1 to code
current = current.right
output code to bitstream
// Output 8-bit symbol value
for i = 7 downto 0:
bit = (symbol >> i) & 1
append bit to bitstream
// Split NYT: create two new leaves (new symbol and new NYT)
newSymbolNode = createNode(nodeCount)
newSymbolNode.symbol = symbol
newSymbolNode.weight = 1
newNYT = createNode(nodeCount + 1)
newNYT.weight = 0
newNYT.symbol = -1
// Replace NYT with internal node
parent = nytNode.parent
internal = createNode(nodeCount + 2)
internal.weight = 1
internal.left = newNYT
internal.right = newSymbolNode
newSymbolNode.parent = internal
newNYT.parent = internal
internal.parent = parent
if nytNode == parent.left:
parent.left = internal
else:
parent.right = internal
nodeCount += 3
leaf = newSymbolNode // For update
UpdateFrequencies(leaf)
procedure Encode(symbol, tree, bitstream)
if symbol is in tree:
current = root
code = empty bit string
while current is not leaf:
if symbol is in left subtree:
append 0 to code
current = current.left
else:
append 1 to code
current = current.right
output code to bitstream
leaf = current // For update
else: // New symbol
current = root
code = empty bit string
nytNode = findNYT(tree) // Locate current NYT leaf
while current != nytNode:
if nytNode is in left subtree of current:
append 0 to code
current = current.left
else:
append 1 to code
current = current.right
output code to bitstream
// Output 8-bit symbol value
for i = 7 downto 0:
bit = (symbol >> i) & 1
append bit to bitstream
// Split NYT: create two new leaves (new symbol and new NYT)
newSymbolNode = createNode(nodeCount)
newSymbolNode.symbol = symbol
newSymbolNode.weight = 1
newNYT = createNode(nodeCount + 1)
newNYT.weight = 0
newNYT.symbol = -1
// Replace NYT with internal node
parent = nytNode.parent
internal = createNode(nodeCount + 2)
internal.weight = 1
internal.left = newNYT
internal.right = newSymbolNode
newSymbolNode.parent = internal
newNYT.parent = internal
internal.parent = parent
if nytNode == parent.left:
parent.left = internal
else:
parent.right = internal
nodeCount += 3
leaf = newSymbolNode // For update
UpdateFrequencies(leaf)
Update Pseudocode
After encoding, frequencies are updated by incrementing weights along the path from the relevant leaf to the root. In the general FGK approach, this involves swapping the node with its higher-numbered sibling of equal or lesser weight if needed to maintain the sibling property, then incrementing. General increment and swap (FGK):procedure Update(leaf)
q = [leaf](/page/Leaf)
while q is not null:
// Swap with highest-numbered node of same weight if needed (sibling property)
if q needs swap: // e.g., q is not highest-numbered of weight q.weight
swap q with highest_numbered_node_of_weight(q.weight)
q.weight += 1
// Update parent weights as sums if needed
q = q.parent
procedure Update(leaf)
q = [leaf](/page/Leaf)
while q is not null:
// Swap with highest-numbered node of same weight if needed (sibling property)
if q needs swap: // e.g., q is not highest-numbered of weight q.weight
swap q with highest_numbered_node_of_weight(q.weight)
q.weight += 1
// Update parent weights as sums if needed
q = q.parent
procedure SlideAndIncrement(p)
wt = p.weight
// Identify block: nodes of same weight, leaves before internals
b = next block after p's block
slide = false
if (p is leaf and b starts with internal nodes of weight wt) or
(p is internal and b starts with leaves of weight wt + 1):
slide = true
// Slide p past nodes in b to maintain order
reorder p to follow b appropriately
p.weight = wt + 1
// Propagate up: repeat for parent if necessary
if p.parent != null:
SlideAndIncrement(p.parent)
procedure SlideAndIncrement(p)
wt = p.weight
// Identify block: nodes of same weight, leaves before internals
b = next block after p's block
slide = false
if (p is leaf and b starts with internal nodes of weight wt) or
(p is internal and b starts with leaves of weight wt + 1):
slide = true
// Slide p past nodes in b to maintain order
reorder p to follow b appropriately
p.weight = wt + 1
// Propagate up: repeat for parent if necessary
if p.parent != null:
SlideAndIncrement(p.parent)
Decoding Counterpart
Decoding mirrors encoding: the receiver traverses the tree using incoming bits to reach a leaf. If NYT is reached, the next 8 bits form the symbol value to introduce the new symbol and split NYT identically to encoding. Frequencies are updated symmetrically to keep trees synchronized. Pseudocode for decoding (symmetric to encoding):function Decode(bitstream, tree)
current = root
while current is not leaf:
bit = read next bit from bitstream
if bit == 0:
current = current.left
else:
current = current.right
if current.symbol != -1: // Known symbol
symbol = current.symbol
leaf = current
else: // NYT reached
symbol = 0
for i = 7 downto 0:
bit = read next bit from bitstream
symbol = (symbol << 1) | bit
// Split NYT identically as in encoding, using symbol value
// (create new nodes with newSymbolNode.symbol = symbol, update tree structure)
leaf = the new symbol node created
UpdateFrequencies(leaf) // Mirror sender's update
return symbol
function Decode(bitstream, tree)
current = root
while current is not leaf:
bit = read next bit from bitstream
if bit == 0:
current = current.left
else:
current = current.right
if current.symbol != -1: // Known symbol
symbol = current.symbol
leaf = current
else: // NYT reached
symbol = 0
for i = 7 downto 0:
bit = read next bit from bitstream
symbol = (symbol << 1) | bit
// Split NYT identically as in encoding, using symbol value
// (create new nodes with newSymbolNode.symbol = symbol, update tree structure)
leaf = the new symbol node created
UpdateFrequencies(leaf) // Mirror sender's update
return symbol