Binary tree

A simple, informal approach to describe a binary tree might be as follows:

a binary tree has a root node, which has 0 or 2 children nodes (which in turn may have their 0 or 2 children, and so on).

More formally:

• (base case) There exists a full tree consisting of a single node;
• (recursive step) If T₁ and T₂ are full binary trees, which do not share any node, and r is a node not belonging to T₁ or T₂, then the ordered triple (r, T₁, T₂) is a full binary tree.^[11]

This definition implies two limitations: a full binary tree contains at least one node, and no node can have only one child. This is resolved with the next definition.

The extended tree definition starts with the assumption the tree can be empty.

• (base case) An empty set of nodes is an extended binary tree.
• (recursive step) If T₁ and T₂ are extended binary trees, which do not share any node, and r is a node not belonging to any of them, then the ordered triple (r, T₁, T₂) is an extended binary tree.^[12][11]

To be complete from the graph point of view, both definitions of a tree should be extended by a definition of the corresponding branches sets. Informally, the branches set can be described as a set of all ordered pairs of nodes (r, s) where r is a root node of any subtree appearing in the definition, and s is a root node of any of its T₁ and T₂ subtrees (in case the respective subtree is not empty).

Another way of imagining this construction (and understanding the terminology) is to consider instead of the empty set a different type of node—for instance square nodes if the regular ones are circles.^[13]

A binary tree is a rooted tree that is also an ordered tree (a.k.a. plane tree) in which every node has at most two children. A rooted tree naturally imparts a notion of levels (distance from the root); thus, for every node, a notion of children may be defined as the nodes connected to it a level below. Ordering of these children (e.g., by drawing them on a plane) makes it possible to distinguish a left child from a right child.^[14] But this still does not distinguish between a node with left but not a right child from a node with right but no left child.

The necessary distinction can be made by first partitioning the edges; i.e., defining the binary tree as triplet (V, E₁, E₂), where (V, E₁ ∪ E₂) is a rooted tree (equivalently arborescence) and E₁ ∩ E₂ is empty, and also requiring that for all j ∈ { 1, 2 }, every node has at most one E_j child.^[15] A more informal way of making the distinction is to say, quoting the Encyclopedia of Mathematics, that "every node has a left child, a right child, neither, or both" and to specify that these "are all different" binary trees.^[7]

Tree terminology is not well-standardized and therefore may vary among examples in the available literature.

• A rooted binary tree has a root node and every node has at most two children.

• A full binary tree (sometimes referred to as a proper,^[16] plane, or strict binary tree)^[17][18] is a tree in which every node has either 0 or 2 children. Another way of defining a full binary tree is a recursive definition. A full binary tree is either:^[12]
  • A single vertex (a single node as the root node).
  • A tree whose root node has two subtrees, both of which are full binary trees.
• A perfect binary tree is a binary tree in which all interior nodes have two children and all leaves have the same depth or same level (the level of a node defined as the number of edges or links from the root node to a node).^[19] A perfect binary tree is a full binary tree.
• A complete binary tree is a binary tree in which every level, except possibly the last, is completely filled, and all nodes in the last level are as far left as possible. It can have between 1 and 2^h nodes at the last level h.^[20] A perfect tree is therefore always complete but a complete tree is not always perfect. Some authors use the term complete to refer instead to a perfect binary tree as defined above, in which case they call this type of tree (with a possibly not filled last level) an almost complete binary tree or nearly complete binary tree.^[21][22] A complete binary tree can be efficiently represented using an array.^[20]

• The infinite complete binary tree is a tree with ${\displaystyle {\aleph _{0}}}$ levels, where for each level d the number of existing nodes at level d is equal to 2^d. The cardinal number of the set of all levels is ${\displaystyle {\aleph _{0}}}$ (countably infinite). The cardinal number of the set of all paths (the "leaves", so to speak) is uncountable, having the cardinality of the continuum.
• A balanced binary tree is a binary tree structure in which the left and right subtrees of every node differ in height (the number of edges from the top-most node to the farthest node in a subtree) by no more than 1 (or the skew is no greater than 1).^[23] One may also consider binary trees where no leaf is much farther away from the root than any other leaf. (Different balancing schemes allow different definitions of "much farther".^[24])
• A degenerate (or pathological) tree is where each parent node has only one associated child node.^[25] This means that the tree will behave like a linked list data structure. In this case, an advantage of using a binary tree is significantly reduced because it is essentially a linked list which time complexity is O(n) (n as the number of nodes and 'O()' being the Big O notation) and it has more data space than the linked list due to two pointers per node, while the complexity of O(log₂ n) for data search in a balanced binary tree is normally expected.

• The number of nodes n in a full binary tree is at least ${\displaystyle 2h+1}$ and at most ${\displaystyle 2^{h+1}-1}$ (i.e., the number of nodes in a perfect binary tree), where h is the height of the tree. A tree consisting of only a root node has a height of 0. The least number of nodes is obtained by adding only two children nodes per adding height so ${\displaystyle 2h+1}$ (1 for counting the root node). The maximum number of nodes is obtained by fully filling nodes at each level, i.e., it is a perfect tree. For a perfect tree, the number of nodes is ${\displaystyle 1+2+4+\ldots +2^{h}=2^{h+1}-1}$, where the last equality is from the geometric series sum.
• The number of leaf nodes l in a perfect binary tree is ${\displaystyle l=(n+1)/2}$ (where n is the number of nodes in the tree) because ${\displaystyle n={{2}^{h+1}}-1}$ (by using the above property) and the number of leaves is ${\displaystyle 2^{h}}$ so ${\displaystyle n=2\cdot {{2}^{h}}-1=2l-1\to l=\left(n+1\right)/2}$. It also means that ${\displaystyle n=2l-1}$. In terms of the tree height h, ${\displaystyle l=(2^{h+1}-1+1)/2=2^{h}}$.
• For any non-empty binary tree with ${\displaystyle l}$ leaf nodes and ${\displaystyle i_{2}}$ nodes of degree 2 (internal nodes with two child nodes), ${\displaystyle l=i_{2}+1}$.^[26] The proof is the following. For a perfect binary tree, the total number of nodes is ${\displaystyle n=2^{h+1}-1}$ (A perfect binary tree is a full binary tree.) and ${\displaystyle l=2^{h}}$, so ${\displaystyle i=n-l=(2^{h+1}-1)-2^{h}=2^{h}-1=l-1\to l=i+1}$. To make a full binary tree from a perfect binary tree, a pair of two sibling nodes are removed one by one. This results in "two leaf nodes removed" and "one internal node removed" and "the removed internal node becoming a leaf node", so one leaf node and one internal node is removed per removing two sibling nodes. As a result, ${\displaystyle l=i+1}$ also holds for a full binary tree. To make a binary tree with a leaf node without its sibling, a single leaf node is removed from a full binary tree, then "one leaf node removed" and "one internal nodes with two children removed" so ${\displaystyle l=i+1}$ also holds. This relation now covers all non-empty binary trees.
• With given n nodes, the minimum possible tree height is ${\displaystyle h_{\min }=\log _{2}(n+1)-1}$ with which the tree is a balanced full tree or perfect tree. With a given height h, the number of nodes can't exceed the ${\displaystyle 2^{h+1}-1}$ as the number of nodes in a perfect tree. Thus ${\displaystyle n\leq 2^{h+1}-1\to h\geq \log _{2}(n+1)-1}$.
• A binary Tree with l leaves has at least the height ${\displaystyle h_{m}=\log _{2}(l)}$. With a given height h, the number of leaves at that height can't exceed ${\displaystyle 2^{h}}$ as the number of leaves at the height in a perfect tree. Thus ${\displaystyle l\leq 2^{h}\to h\geq \log _{2}(l)}$.
• In a non-empty binary tree, if n is the total number of nodes and e is the total number of edges, then ${\displaystyle e=n-1}$. This is obvious because each node requires one edge except for the root node.
• The number of null links (i.e., absent children of the nodes) in a binary tree of n nodes is (n + 1).
• The number of internal nodes in a complete binary tree of n nodes is ${\displaystyle \lfloor n/2\rfloor }$.

This section does not cite any sources. Please help improve this section by adding citations to reliable sources. Unsourced material may be challenged and removed. (July 2014) (Learn how and when to remove this message)

In combinatorics, one considers the problem of counting the number of full binary trees of a given size. Here the trees have no values attached to their nodes (this would just multiply the number of possible trees by an easily determined factor), and trees are distinguished only by their structure; however, the left and right child of any node are distinguished (if they are different trees, then interchanging them will produce a tree distinct from the original one). The size of the tree is taken to be the number n of internal nodes (those with two children); the other nodes are leaf nodes and there are n + 1 of them. The number of such binary trees of size n is equal to the number of ways of fully parenthesizing a string of n + 1 symbols (representing leaves) separated by n binary operators (representing internal nodes), to determine the argument subexpressions of each operator. For instance for n = 3 one has to parenthesize a string like ⁠${\displaystyle X*X*X*X}$⁠, which is possible in five ways:

$${\displaystyle ((X*X)*X)*X,\qquad (X*(X*X))*X,\qquad (X*X)*(X*X),\qquad X*((X*X)*X),\qquad X*(X*(X*X)).}$$

The correspondence to binary trees should be obvious, and the addition of redundant parentheses (around an already parenthesized expression or around the full expression) is disallowed (or at least not counted as producing a new possibility).

There is a unique binary tree of size 0 (consisting of a single leaf), and any other binary tree is characterized by the pair of its left and right children; if these have sizes i and j respectively, the full tree has size i + j + 1. Therefore, the number ${\displaystyle C_{n}}$ of binary trees of size n has the following recursive description ${\displaystyle C_{0}=1}$, and ${\displaystyle \textstyle C_{n}=\sum _{i=0}^{n-1}C_{i}C_{n-1-i}}$ for any positive integer n. It follows that ${\displaystyle C_{n}}$ is the Catalan number of index n.

The above parenthesized strings should not be confused with the set of words of length 2n in the Dyck language, which consist only of parentheses in such a way that they are properly balanced. The number of such strings satisfies the same recursive description (each Dyck word of length 2n is determined by the Dyck subword enclosed by the initial '(' and its matching ')' together with the Dyck subword remaining after that closing parenthesis, whose lengths 2i and 2j satisfy i + j + 1 = n); this number is therefore also the Catalan number ${\displaystyle C_{n}}$. So there are also five Dyck words of length 6:

()()(),     ()(()),     (())(),     (()()),     ((()))

These Dyck words do not correspond to binary trees in the same way. Instead, they are related by the following recursively defined bijection: the Dyck word equal to the empty string corresponds to the binary tree of size 0 with only one leaf. Any other Dyck word can be written as (${\displaystyle w_{1}}$)${\displaystyle w_{2}}$, where ${\displaystyle w_{1}}$,${\displaystyle w_{2}}$ are themselves (possibly empty) Dyck words and where the two written parentheses are matched. The bijection is then defined by letting the words ${\displaystyle w_{1}}$ and ${\displaystyle w_{2}}$ correspond to the binary trees that are the left and right children of the root.

A bijective correspondence can also be defined as follows: enclose the Dyck word in an extra pair of parentheses, so that the result can be interpreted as a Lisp list expression (with the empty list () as only occurring atom); then the dotted-pair expression for that proper list is a fully parenthesized expression (with NIL as symbol and '.' as operator) describing the corresponding binary tree (which is, in fact, the internal representation of the proper list).

The ability to represent binary trees as strings of symbols and parentheses implies that binary trees can represent the elements of a free magma on a singleton set.

Binary trees can be constructed from programming language primitives in several ways.

In a language with records and references, binary trees are typically constructed by having a tree node structure which contains some data and references to its left child and its right child. Sometimes it also contains a reference to its unique parent. If a node has fewer than two children, some of the child pointers may be set to a special null value, or to a special sentinel node.

This method of storing binary trees wastes a fair bit of memory, as the pointers will be null (or point to the sentinel) more than half the time; a more conservative representation alternative is threaded binary tree.^[27]

In languages with tagged unions such as ML, a tree node is often a tagged union of two types of nodes, one of which is a 3-tuple of data, left child, and right child, and the other of which is a "leaf" node, which contains no data and functions much like the null value in a language with pointers. For example, the following line of code in OCaml (an ML dialect) defines a binary tree that stores a character in each node.^[28]

type chr_tree = Empty | Node of char * chr_tree * chr_tree

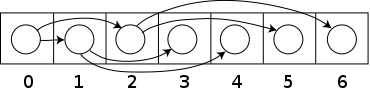
Binary trees can also be stored in breadth-first order as an implicit data structure in arrays, and if the tree is a complete binary tree, this method wastes no space. In this compact arrangement, if a node has an index i, its children are found at indices ${\displaystyle 2i+1}$ (for the left child) and ${\displaystyle 2i+2}$ (for the right), while its parent (if any) is found at index ${\displaystyle \left\lfloor {\frac {i-1}{2}}\right\rfloor }$ (assuming the root has index zero). Alternatively, with a 1-indexed array, the implementation is simplified with children found at ${\displaystyle 2i}$ and ${\displaystyle 2i+1}$, and parent found at ${\displaystyle \lfloor i/2\rfloor }$.^[29]

This method benefits from more compact storage and better locality of reference, particularly during a preorder traversal. It is often used for binary heaps.^[30]

A succinct data structure is one which occupies close to minimum possible space, as established by information theoretical lower bounds. The number of different binary trees on ${\displaystyle n}$ nodes is ${\displaystyle \mathrm {C} _{n}}$, the ${\displaystyle n}$th Catalan number (assuming we view trees with identical structure as identical). For large ${\displaystyle n}$, this is about ${\displaystyle 4^{n}}$; thus we need at least about ${\displaystyle \log _{2}4^{n}=2n}$ bits to encode it. A succinct binary tree therefore would occupy 2n+o(n) bits (with 'o()' being the Little-o notation).

One simple representation which meets this bound is to visit the nodes of the tree in preorder, outputting "1" for an internal node and "0" for a leaf.^[31] If the tree contains data, we can simply simultaneously store it in a consecutive array in preorder. This function accomplishes this:

function EncodeSuccinct(node n, bitstring structure, array data) {
    if n = nil then
        append 0 to structure;
    else
        append 1 to structure;
        append n.data to data;
        EncodeSuccinct(n.left, structure, data);
        EncodeSuccinct(n.right, structure, data);
}

The string structure has only ${\displaystyle 2n+1}$ bits in the end, where ${\displaystyle n}$ is the number of (internal) nodes; we don't even have to store its length. To show that no information is lost, we can convert the output back to the original tree like this:

function DecodeSuccinct(bitstring structure, array data) {
    remove first bit of structure and put it in b
    if b = 1 then
        create a new node n
        remove first element of data and put it in n.data
        n.left = DecodeSuccinct(structure, data)
        n.right = DecodeSuccinct(structure, data)
        return n
    else
        return nil
}

More sophisticated succinct representations allow not only compact storage of trees but even useful operations on those trees directly while they're still in their succinct form.

There is a natural one-to-one correspondence between ordered trees and binary trees. It allows any ordered tree to be uniquely represented as a binary tree, and vice versa:

Let T be a node of an ordered tree, and let B denote T's image in the corresponding binary tree. Then B's left child represents T's first child, while the B's right child represents T's next sibling.

For example, the ordered tree on the left and the binary tree on the right correspond:

In the pictured binary tree, the black, left, edges represent first child, while the blue, right, edges represent next sibling.

This representation is called a left-child right-sibling binary tree.

There are a variety of different operations that can be performed on binary trees. Some are mutator operations, while others simply return useful information about the tree.

Nodes can be inserted into binary trees in between two other nodes or added after a leaf node. In binary trees, a node that is inserted is specified as to whose child it will be.

To add a new node after leaf node A, A assigns the new node as one of its children and the new node assigns node A as its parent.

Insertion on internal nodes is slightly more complex than on leaf nodes. Say that the internal node is node A and that node B is the child of A. (If the insertion is to insert a right child, then B is the right child of A, and similarly with a left child insertion.) A assigns its child to the new node and the new node assigns its parent to A. Then the new node assigns its child to B and B assigns its parent as the new node.

Deletion is the process whereby a node is removed from the tree. Only certain nodes in a binary tree can be removed unambiguously.^[32]

Suppose that the node to delete is node A. If A has no children, deletion is accomplished by setting the child of A's parent to null. If A has one child, set the parent of A's child to A's parent and set the child of A's parent to A's child.

In a binary tree, a node with two children cannot be deleted unambiguously.^[32] However, in certain binary trees (including binary search trees) these nodes can be deleted, though with a rearrangement of the tree structure.

Pre-order, in-order, and post-order traversal visit each node in a tree by recursively visiting each node in the left and right subtrees of the root. Below are the brief descriptions of above mentioned traversals.

In pre-order, we always visit the current node; next, we recursively traverse the current node's left subtree, and then we recursively traverse the current node's right subtree. The pre-order traversal is a topologically sorted one, because a parent node is processed before any of its child nodes is done.

In in-order, we always recursively traverse the current node's left subtree; next, we visit the current node, and lastly, we recursively traverse the current node's right subtree.

In post-order, we always recursively traverse the current node's left subtree; next, we recursively traverse the current node's right subtree and then visit the current node. Post-order traversal can be useful to get postfix expression of a binary expression tree.^[33]

In depth-first order, we always attempt to visit the node farthest from the root node that we can, but with the caveat that it must be a child of a node we have already visited. Unlike a depth-first search on graphs, there is no need to remember all the nodes we have visited, because a tree cannot contain cycles. Pre-order is a special case of this. See depth-first search for more information.

Contrasting with depth-first order is breadth-first order, which always attempts to visit the node closest to the root that it has not already visited. See breadth-first search for more information. Also called a level-order traversal.

In a complete binary tree, a node's breadth-index (i − (2^d − 1)) can be used as traversal instructions from the root. Reading bitwise from left to right, starting at bit d − 1, where d is the node's distance from the root (d = ⌊log₂(i+1)⌋) and the node in question is not the root itself (d > 0). When the breadth-index is masked at bit d − 1, the bit values 0 and 1 mean to step either left or right, respectively. The process continues by successively checking the next bit to the right until there are no more. The rightmost bit indicates the final traversal from the desired node's parent to the node itself. There is a time-space trade-off between iterating a complete binary tree this way versus each node having pointer(s) to its sibling(s).