Coefficient of determination

A data set has n values marked y₁, ..., y_n (collectively known as y_i or as a vector y = [y₁, ..., y_n]^T), each associated with a fitted (or modeled, or predicted) value f₁, ..., f_n (known as f_i, or sometimes ŷ_i, as a vector f).

Define the residuals as e_i = y_i − f_i (forming a vector e).

If ${\displaystyle {\bar {y}}}$ is the mean of the observed data: $${\displaystyle {\bar {y}}={\frac {1}{n}}\sum _{i=1}^{n}y_{i}}$$ then the variability of the data set can be measured with two sums of squares formulas:

• The sum of squares of residuals, also called the residual sum of squares: $${\displaystyle SS_{\text{res}}=\sum _{i}(y_{i}-f_{i})^{2}=\sum _{i}e_{i}^{2}\,}$$
• The total sum of squares (proportional to the variance of the data): $${\displaystyle SS_{\text{tot}}=\sum _{i}(y_{i}-{\bar {y}})^{2}}$$

The most general definition of the coefficient of determination is $${\displaystyle R^{2}=1-{SS_{\rm {res}} \over SS_{\rm {tot}}}}$$

In the best case, the modeled values exactly match the observed values, which results in ${\displaystyle SS_{\text{res}}=0}$ and R² = 1. A baseline model, which always predicts y, will have R² = 0.

In a general form, R² can be seen to be related to the fraction of variance unexplained (FVU), since the second term compares the unexplained variance (variance of the model's errors) with the total variance (of the data): $${\displaystyle R^{2}=1-{\text{FVU}}}$$

A larger value of R² implies a more successful regression model.^[4]: 463 Suppose R² = 0.49. This implies that 49% of the variability of the dependent variable in the data set has been accounted for, and the remaining 51% of the variability is still unaccounted for. For regression models, the regression sum of squares, also called the explained sum of squares, is defined as

${\displaystyle SS_{\text{reg}}=\sum _{i}(f_{i}-{\bar {y}})^{2}}$

In some cases, as in simple linear regression, the total sum of squares equals the sum of the two other sums of squares defined above:

${\displaystyle SS_{\text{res}}+SS_{\text{reg}}=SS_{\text{tot}}}$

See Partitioning in the general OLS model for a derivation of this result for one case where the relation holds. When this relation does hold, the above definition of R² is equivalent to

${\displaystyle R^{2}={\frac {SS_{\text{reg}}}{SS_{\text{tot}}}}={\frac {SS_{\text{reg}}/n}{SS_{\text{tot}}/n}}}$

where n is the number of observations (cases) on the variables.

In this form R² is expressed as the ratio of the explained variance (variance of the model's predictions, which is SS_reg / n) to the total variance (sample variance of the dependent variable, which is SS_tot / n).

This partition of the sum of squares holds for instance when the model values ƒ_i have been obtained by linear regression. A milder sufficient condition reads as follows: The model has the form

${\displaystyle f_{i}={\widehat {\alpha }}+{\widehat {\beta }}q_{i}}$

where the q_i are arbitrary values that may or may not depend on i or on other free parameters (the common choice q_i = x_i is just one special case), and the coefficient estimates ${\displaystyle {\widehat {\alpha }}}$ and ${\displaystyle {\widehat {\beta }}}$ are obtained by minimizing the residual sum of squares.

This set of conditions is an important one and it has a number of implications for the properties of the fitted residuals and the modelled values. In particular, under these conditions:

${\displaystyle {\bar {f}}={\bar {y}}.\,}$

In linear least squares multiple regression (with fitted intercept and slope), R² equals ${\displaystyle \rho ^{2}(y,f)}$ the square of the Pearson correlation coefficient between the observed ${\displaystyle y}$ and modeled (predicted) ${\displaystyle f}$ data values of the dependent variable.

In a linear least squares regression with a single explanator (with fitted intercept and slope), this is also equal to ${\displaystyle \rho ^{2}(y,x)}$ the squared Pearson correlation coefficient between the dependent variable ${\displaystyle y}$ and explanatory variable ${\displaystyle x}$.

It should not be confused with the correlation coefficient between two explanatory variables, defined as

${\displaystyle \rho _{{\widehat {\alpha }},{\widehat {\beta }}}={\operatorname {cov} \left({\widehat {\alpha }},{\widehat {\beta }}\right) \over \sigma _{\widehat {\alpha }}\sigma _{\widehat {\beta }}},}$

where the covariance between two coefficient estimates, as well as their standard deviations, are obtained from the covariance matrix of the coefficient estimates, ${\displaystyle (X^{T}X)^{-1}}$.

Under more general modeling conditions, where the predicted values might be generated from a model different from linear least squares regression, an R² value can be calculated as the square of the correlation coefficient between the original ${\displaystyle y}$ and modeled ${\displaystyle f}$ data values. In this case, the value is not directly a measure of how good the modeled values are, but rather a measure of how good a predictor might be constructed from the modeled values (by creating a revised predictor of the form α + βƒ_i).^{[citation needed]} According to Everitt,^[10] this usage is specifically the definition of the term "coefficient of determination": the square of the correlation between two (general) variables.

R² is a measure of the goodness of fit of a model.^[11] In regression, the R² coefficient of determination is a statistical measure of how well the regression predictions approximate the real data points. An R² of 1 indicates that the regression predictions perfectly fit the data.

Values of R² outside the range 0 to 1 occur when the model fits the data worse than the worst possible least-squares predictor (equivalent to a horizontal hyperplane at a height equal to the mean of the observed data). This occurs when a wrong model was chosen, or nonsensical constraints were applied by mistake. If equation 1 of Kvålseth^[12] is used (this is the equation used most often), R² can be less than zero. If equation 2 of Kvålseth is used, R² can be greater than one.

In all instances where R² is used, the predictors are calculated by ordinary least-squares regression: that is, by minimizing SS_res. In this case, R² increases as the number of variables in the model is increased (R² is monotone increasing with the number of variables included—it will never decrease). This illustrates a drawback to one possible use of R², where one might keep adding variables (kitchen sink regression) to increase the R² value. For example, if one is trying to predict the sales of a model of car from the car's gas mileage, price, and engine power, one can include probably irrelevant factors such as the first letter of the model's name or the height of the lead engineer designing the car because the R² will never decrease as variables are added and will likely experience an increase due to chance alone.

This leads to the alternative approach of looking at the adjusted R². The explanation of this statistic is almost the same as R² but it penalizes the statistic as extra variables are included in the model. For cases other than fitting by ordinary least squares, the R² statistic can be calculated as above and may still be a useful measure. If fitting is by weighted least squares or generalized least squares, alternative versions of R² can be calculated appropriate to those statistical frameworks, while the "raw" R² may still be useful if it is more easily interpreted. Values for R² can be calculated for any type of predictive model, which need not have a statistical basis.

Consider a linear model with more than a single explanatory variable, of the form

${\displaystyle Y_{i}=\beta _{0}+\sum _{j=1}^{p}\beta _{j}X_{i,j}+\varepsilon _{i},}$

where, for the ith case, ${\displaystyle {Y_{i}}}$ is the response variable, ${\displaystyle X_{i,1},\dots ,X_{i,p}}$ are p regressors, and ${\displaystyle \varepsilon _{i}}$ is a mean zero error term. The quantities ${\displaystyle \beta _{0},\dots ,\beta _{p}}$ are unknown coefficients, whose values are estimated by least squares. The coefficient of determination R² is a measure of the global fit of the model. Specifically, R² is an element of [0, 1] and represents the proportion of variability in Y_i that may be attributed to some linear combination of the regressors (explanatory variables) in X.^[13]

R² is often interpreted as the proportion of response variation "explained" by the regressors in the model. Thus, R² = 1 indicates that the fitted model explains all variability in ${\displaystyle y}$, while R² = 0 indicates no 'linear' relationship (for straight line regression, this means that the straight line model is a constant line (slope = 0, intercept = ${\displaystyle {\bar {y}}}$) between the response variable and regressors). An interior value such as R² = 0.7 may be interpreted as follows: "Seventy percent of the variance in the response variable can be explained by the explanatory variables. The remaining thirty percent can be attributed to unknown, lurking variables or inherent variability."

A caution that applies to R², as to other statistical descriptions of correlation and association is that "correlation does not imply causation". In other words, while correlations may sometimes provide valuable clues in uncovering causal relationships among variables, a non-zero estimated correlation between two variables is not, on its own, evidence that changing the value of one variable would result in changes in the values of other variables. For example, the practice of carrying matches (or a lighter) is correlated with incidence of lung cancer, but carrying matches does not cause cancer (in the standard sense of "cause").

In case of a single regressor, fitted by least squares, R² is the square of the Pearson product-moment correlation coefficient relating the regressor and the response variable. More generally, R² is the square of the correlation between the constructed predictor and the response variable. With more than one regressor, the R² can be referred to as the coefficient of multiple determination.

In least squares regression using typical data, R² is at least weakly increasing with an increase in number of regressors in the model. Because increases in the number of regressors increase the value of R², R² alone cannot be used as a meaningful comparison of models with very different numbers of independent variables. For a meaningful comparison between two models, an F-test can be performed on the residual sum of squares ^{[citation needed]}, similar to the F-tests in Granger causality, though this is not always appropriate^{[further explanation needed]}. As a reminder of this, some authors denote R² by R_q², where q is the number of columns in X (the number of explanators including the constant).

To demonstrate this property, first recall that the objective of least squares linear regression is

${\displaystyle \min _{b}SS_{\text{res}}(b)\Rightarrow \min _{b}\sum _{i}(y_{i}-X_{i}b)^{2}\,}$

where X_i is a row vector of values of explanatory variables for case i and b is a column vector of coefficients of the respective elements of X_i.

The optimal value of the objective is weakly smaller as more explanatory variables are added and hence additional columns of ${\displaystyle X}$ (the explanatory data matrix whose ith row is X_i) are added, by the fact that less constrained minimization leads to an optimal cost which is weakly smaller than more constrained minimization does. Given the previous conclusion and noting that ${\displaystyle SS_{tot}}$ depends only on y, the non-decreasing property of R² follows directly from the definition above.

The intuitive reason that using an additional explanatory variable cannot lower the R² is this: Minimizing ${\displaystyle SS_{\text{res}}}$ is equivalent to maximizing R². When the extra variable is included, the data always have the option of giving it an estimated coefficient of zero, leaving the predicted values and the R² unchanged. The only way that the optimization problem will give a non-zero coefficient is if doing so improves the R².

The above gives an analytical explanation of the inflation of R². Next, an example based on ordinary least square from a geometric perspective is shown below.^[14]

A simple case to be considered first:

${\displaystyle Y=\beta _{0}+\beta _{1}\cdot X_{1}+\varepsilon \,}$

This equation describes the ordinary least squares regression model with one regressor. The prediction is shown as the red vector in the figure on the right. Geometrically, it is the projection of true value onto a model space in ${\displaystyle \mathbb {R} }$ (without intercept). The residual is shown as the red line.

${\displaystyle Y=\beta _{0}+\beta _{1}\cdot X_{1}+\beta _{2}\cdot X_{2}+\varepsilon \,}$

This equation corresponds to the ordinary least squares regression model with two regressors. The prediction is shown as the blue vector in the figure on the right. Geometrically, it is the projection of true value onto a larger model space in ${\displaystyle \mathbb {R} ^{2}}$ (without intercept). Noticeably, the values of ${\displaystyle \beta _{0}}$ and ${\displaystyle \beta _{0}}$ are not the same as in the equation for smaller model space as long as ${\displaystyle X_{1}}$ and ${\displaystyle X_{2}}$ are not zero vectors. Therefore, the equations are expected to yield different predictions (i.e., the blue vector is expected to be different from the red vector). The least squares regression criterion ensures that the residual is minimized. In the figure, the blue line representing the residual is orthogonal to the model space in ${\displaystyle \mathbb {R} ^{2}}$, giving the minimal distance from the space.

The smaller model space is a subspace of the larger one, and thereby the residual of the smaller model is guaranteed to be larger. Comparing the red and blue lines in the figure, the blue line is orthogonal to the space, and any other line would be larger than the blue one. Considering the calculation for R², a smaller value of ${\displaystyle SS_{tot}}$ will lead to a larger value of R², meaning that adding regressors will result in inflation of R².

R² does not indicate whether:

• the independent variables are a cause of the changes in the dependent variable;
• omitted-variable bias exists;
• the correct regression was used;
• the most appropriate set of independent variables has been chosen;
• there is collinearity present in the data on the explanatory variables;
• the model might be improved by using transformed versions of the existing set of independent variables;
• there are enough data points to make a solid conclusion;
• there are a few outliers in an otherwise good sample.

The use of an adjusted R² (one common notation is ${\displaystyle {\bar {R}}^{2}}$, pronounced "R bar squared"; another is ${\displaystyle R_{\text{a}}^{2}}$ or ${\displaystyle R_{\text{adj}}^{2}}$) is an attempt to account for the phenomenon of the R² automatically increasing when extra explanatory variables are added to the model. There are many different ways of adjusting.^[15] By far the most used one, to the point that it is typically just referred to as adjusted R, is the correction proposed by Mordecai Ezekiel.^[15][16][17] The adjusted R² is defined as

${\displaystyle {\bar {R}}^{2}={1-{SS_{\text{res}}/{\text{df}}_{\text{res}} \over SS_{\text{tot}}/{\text{df}}_{\text{tot}}}}}$

where df_res is the degrees of freedom of the estimate of the population variance around the model, and df_tot is the degrees of freedom of the estimate of the population variance around the mean. df_res is given in terms of the sample size n and the number of variables p in the model, df_res = n − p − 1. df_tot is given in the same way, but with p being zero for the mean (i.e., df_tot = n − 1).

Inserting the degrees of freedom and using the definition of R², it can be rewritten as:

${\displaystyle {\bar {R}}^{2}=1-(1-R^{2}){n-1 \over n-p-1}}$

where p is the total number of explanatory variables in the model (excluding the intercept), and n is the sample size.

The adjusted R² can be negative, and its value will always be less than or equal to that of R². Unlike R², the adjusted R² increases only when the increase in R² (due to the inclusion of a new explanatory variable) is more than one would expect to see by chance. If a set of explanatory variables with a predetermined hierarchy of importance are introduced into a regression one at a time, with the adjusted R² computed each time, the level at which adjusted R² reaches a maximum, and decreases afterward, would be the regression with the ideal combination of having the best fit without excess/unnecessary terms.

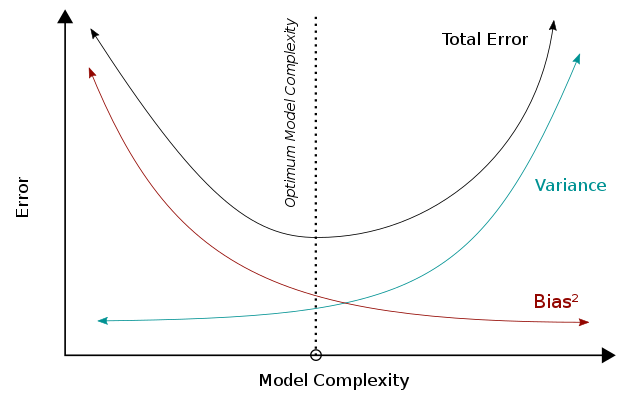
The adjusted R² can be interpreted as an instance of the bias-variance tradeoff. When we consider the performance of a model, a lower error represents a better performance. When the model becomes more complex, the variance will increase whereas the square of bias will decrease, and these two metrics add up to be the total error. Combining these two trends, the bias-variance tradeoff describes a relationship between the performance of the model and its complexity, which is shown as a u-shape curve on the right. For the adjusted R² specifically, the model complexity (i.e. number of parameters) affects the R² and the term / frac and thereby captures their attributes in the overall performance of the model.

R² can be interpreted as the variance of the model, which is influenced by the model complexity. A high R² indicates a lower bias error because the model can better explain the change of Y with predictors. For this reason, we make fewer (erroneous) assumptions, and this results in a lower bias error. Meanwhile, to accommodate fewer assumptions, the model tends to be more complex. Based on bias-variance tradeoff, a higher complexity will lead to a decrease in bias and a better performance (below the optimal line). In R², the term (1 − R²) will be lower with high complexity and resulting in a higher R², consistently indicating a better performance.

On the other hand, the term/frac term is reversely affected by the model complexity. The term/frac will increase when adding regressors (i.e., increased model complexity) and lead to worse performance. Based on bias-variance tradeoff, a higher model complexity (beyond the optimal line) leads to increasing errors and a worse performance.

Considering the calculation of R², more parameters will increase the R² and lead to an increase in R². Nevertheless, adding more parameters will increase the term/frac and thus decrease R². These two trends construct a reverse u-shape relationship between model complexity and R², which is in consistent with the u-shape trend of model complexity versus overall performance. Unlike R², which will always increase when model complexity increases, R² will increase only when the bias eliminated by the added regressor is greater than the variance introduced simultaneously. Using R² instead of R² could thereby prevent overfitting.

Following the same logic, adjusted R² can be interpreted as a less biased estimator of the population R², whereas the observed sample R² is a positively biased estimate of the population value.^[18] Adjusted R² is more appropriate when evaluating model fit (the variance in the dependent variable accounted for by the independent variables) and in comparing alternative models in the feature selection stage of model building.^[18]

The principle behind the adjusted R² statistic can be seen by rewriting the ordinary R² as

${\displaystyle R^{2}={1-{{\text{VAR}}_{\text{res}} \over {\text{VAR}}_{\text{tot}}}}}$

where ${\displaystyle {\text{VAR}}_{\text{res}}=SS_{\text{res}}/n}$ and ${\displaystyle {\text{VAR}}_{\text{tot}}=SS_{\text{tot}}/n}$ are the sample variances of the estimated residuals and the dependent variable respectively, which can be seen as biased estimates of the population variances of the errors and of the dependent variable. These estimates are replaced by statistically unbiased versions: ${\displaystyle {\text{VAR}}_{\text{res}}=SS_{\text{res}}/(n-p)}$ and ${\displaystyle {\text{VAR}}_{\text{tot}}=SS_{\text{tot}}/(n-1)}$.

Despite using unbiased estimators for the population variances of the error and the dependent variable, adjusted R² is not an unbiased estimator of the population R²,^[18] which results by using the population variances of the errors and the dependent variable instead of estimating them. Ingram Olkin and John W. Pratt derived the minimum-variance unbiased estimator for the population R²,^[19] which is known as Olkin–Pratt estimator. Comparisons of different approaches for adjusting R² concluded that in most situations either an approximate version of the Olkin–Pratt estimator ^[18] or the exact Olkin–Pratt estimator ^[20] should be preferred over (Ezekiel) adjusted R².

The coefficient of partial determination can be defined as the proportion of variation that cannot be explained in a reduced model, but can be explained by the predictors specified in a full model.^[21][22][23] This coefficient is used to provide insight into whether or not one or more additional predictors may be useful in a more fully specified regression model.

The calculation for the partial R² is relatively straightforward after estimating two models and generating the ANOVA tables for them. The calculation for the partial R² is

${\displaystyle {\frac {SS_{\text{ res, reduced}}-SS_{\text{ res, full}}}{SS_{\text{ res, reduced}}}},}$

which is analogous to the usual coefficient of determination:

${\displaystyle {\frac {SS_{\text{tot}}-SS_{\text{res}}}{SS_{\text{tot}}}}.}$

As explained above, model selection heuristics such as the adjusted R² criterion and the F-test examine whether the total R² sufficiently increases to determine if a new regressor should be added to the model. If a regressor is added to the model that is highly correlated with other regressors which have already been included, then the total R² will hardly increase, even if the new regressor is of relevance. As a result, the above-mentioned heuristics will ignore relevant regressors when cross-correlations are high.^[24]

Alternatively, one can decompose a generalized version of R² to quantify the relevance of deviating from a hypothesis.^[24] As Hoornweg (2018) shows, several shrinkage estimators – such as Bayesian linear regression, ridge regression, and the (adaptive) lasso – make use of this decomposition of R² when they gradually shrink parameters from the unrestricted OLS solutions towards the hypothesized values. Let us first define the linear regression model as

${\displaystyle y=X\beta +\varepsilon .}$

It is assumed that the matrix X is standardized with Z-scores and that the column vector ${\displaystyle y}$ is centered to have a mean of zero. Let the column vector ${\displaystyle \beta _{0}}$ refer to the hypothesized regression parameters and let the column vector ${\displaystyle b}$ denote the estimated parameters. We can then define

${\displaystyle R^{2}=1-{\frac {(y-Xb)'(y-Xb)}{(y-X\beta _{0})'(y-X\beta _{0})}}.}$

An R² of 75% means that the in-sample accuracy improves by 75% if the data-optimized b solutions are used instead of the hypothesized ${\displaystyle \beta _{0}}$ values. In the special case that ${\displaystyle \beta _{0}}$ is a vector of zeros, we obtain the traditional R² again.

The individual effect on R² of deviating from a hypothesis can be computed with ${\displaystyle R^{\otimes }}$ ('R-outer'). This ${\displaystyle p}$ times ${\displaystyle p}$ matrix is given by

${\displaystyle R^{\otimes }=(X'{\tilde {y}}_{0})(X'{\tilde {y}}_{0})'(X'X)^{-1}({\tilde {y}}_{0}'{\tilde {y}}_{0})^{-1},}$

where ${\displaystyle {\tilde {y}}_{0}=y-X\beta _{0}}$. The diagonal elements of ${\displaystyle R^{\otimes }}$ exactly add up to R². If regressors are uncorrelated and ${\displaystyle \beta _{0}}$ is a vector of zeros, then the ${\displaystyle j^{\text{th}}}$ diagonal element of ${\displaystyle R^{\otimes }}$ simply corresponds to the r² value between ${\displaystyle x_{j}}$ and ${\displaystyle y}$. When regressors ${\displaystyle x_{i}}$ and ${\displaystyle x_{j}}$ are correlated, ${\displaystyle R_{ii}^{\otimes }}$ might increase at the cost of a decrease in ${\displaystyle R_{jj}^{\otimes }}$. As a result, the diagonal elements of ${\displaystyle R^{\otimes }}$ may be smaller than 0 and, in more exceptional cases, larger than 1. To deal with such uncertainties, several shrinkage estimators implicitly take a weighted average of the diagonal elements of ${\displaystyle R^{\otimes }}$ to quantify the relevance of deviating from a hypothesized value.^[24] Click on the lasso for an example.

In the case of logistic regression, usually fit by maximum likelihood, there are several choices of pseudo-R².

One is the generalized R² originally proposed by Cox & Snell,^[25] and independently by Magee:^[26]

${\displaystyle R^{2}=1-\left({{\mathcal {L}}(0) \over {\mathcal {L}}({\widehat {\theta }})}\right)^{2/n}}$

where ${\displaystyle {\mathcal {L}}(0)}$ is the likelihood of the model with only the intercept, ${\displaystyle {{\mathcal {L}}({\widehat {\theta }})}}$ is the likelihood of the estimated model (i.e., the model with a given set of parameter estimates) and n is the sample size. It is easily rewritten to:

${\displaystyle R^{2}=1-e^{{\frac {2}{n}}(\ln({\mathcal {L}}(0))-\ln({\mathcal {L}}({\widehat {\theta }})))}=1-e^{-D/n}}$

where D is the test statistic of the likelihood ratio test.

Nico Nagelkerke noted that it had the following properties:^[27][22]

1. It is consistent with the classical coefficient of determination when both can be computed;
2. Its value is maximised by the maximum likelihood estimation of a model;
3. It is asymptotically independent of the sample size;
4. The interpretation is the proportion of the variation explained by the model;
5. The values are between 0 and 1, with 0 denoting that model does not explain any variation and 1 denoting that it perfectly explains the observed variation;
6. It does not have any unit.

However, in the case of a logistic model, where ${\displaystyle {\mathcal {L}}({\widehat {\theta }})}$ cannot be greater than 1, R² is between 0 and ${\displaystyle R_{\max }^{2}=1-({\mathcal {L}}(0))^{2/n}}$: thus, Nagelkerke suggested the possibility to define a scaled R² as R²/R²_max.^[22]

Occasionally, residual statistics are used for indicating goodness of fit. The norm of residuals is calculated as the square-root of the sum of squares of residuals (SSR):

${\displaystyle {\text{norm of residuals}}={\sqrt {SS_{\text{res}}}}=\|e\|.}$

Similarly, the reduced chi-square is calculated as the SSR divided by the degrees of freedom.

Both R² and the norm of residuals have their relative merits. For least squares analysis R² varies between 0 and 1, with larger numbers indicating better fits and 1 representing a perfect fit. The norm of residuals varies from 0 to infinity with smaller numbers indicating better fits and zero indicating a perfect fit. One advantage and disadvantage of R² is the ${\displaystyle SS_{\text{tot}}}$ term acts to normalize the value. If the y_i values are all multiplied by a constant, the norm of residuals will also change by that constant but R² will stay the same. As a basic example, for the linear least squares fit to the set of data:

x	1	2	3	4	5
y	1.9	3.7	5.8	8.0	9.6

R² = 0.998, and norm of residuals = 0.302. If all values of y are multiplied by 1000 (for example, in an SI prefix change), then R² remains the same, but norm of residuals = 302.

Another single-parameter indicator of fit is the RMSE of the residuals, or standard deviation of the residuals. This would have a value of 0.135 for the above example given that the fit was linear with an unforced intercept.^[28]

The creation of the coefficient of determination has been attributed to the geneticist Sewall Wright and was first published in 1921.^[29]

• Anscombe's quartet
• Fraction of variance unexplained
• Goodness of fit
• Nash–Sutcliffe model efficiency coefficient (hydrological applications)
• Pearson product-moment correlation coefficient
• Proportional reduction in loss
• Regression model validation
• Root mean square deviation
• Stepwise regression