Bubble point

Bubble pointMain

Community hub

Bubble point

8 pages, 0 posts

0 subscribers

Recent from talks

Be the first to start a discussion here.

Recent from talks

Be the first to start a discussion here.

Contribute something

About hubMembersContent overviewUpdatesRules

Main reference articles

Bubble point

View on Wikipedia

from Wikipedia

In thermodynamics, the bubble point is the temperature (at a given pressure) where the first bubble of vapor is formed when heating a liquid consisting of two or more components.^[1]^[2] Given that vapor will probably have a different composition than the liquid, the bubble point (along with the dew point) at different compositions are useful data when designing distillation systems.^[3]

For a single component the bubble point and the dew point are the same and are referred to as the boiling point.

Calculating the bubble point

[edit]

At the bubble point, the following relationship holds:

\sum _{i=1}^{N_{c}}y_{i}=\sum _{i=1}^{N_{c}}K_{i}x_{i}=1

where

K_{i}\equiv {\frac {y_{ie}}{x_{ie}}}

K is the distribution coefficient or K factor, defined as the ratio of mole fraction in the vapor phase ${\big (}y_{ie}{\big )}$ to the mole fraction in the liquid phase ${\big (}x_{ie}{\big )}$ at equilibrium.
When Raoult's law and Dalton's law hold for the mixture, the K factor is defined as the ratio of the vapor pressure to the total pressure of the system:^[1]

K_{i}={\frac {P'_{i}}{P}}

Given either of $x_{i}$ or $y_{i}$ and either the temperature or pressure of a two-component system, calculations can be performed to determine the unknown information.^[4]

References

[edit]

^ ^a ^b McCabe, Warren L.; Smith, Julian C.; Harriot, Peter (2005), Unit Operations of Chemical Engineering (seventh ed.), New York: McGraw-Hill, pp. 737–738, ISBN 0-07-284823-5
^ Smith, J. M.; Van Ness, H. C.; Abbott, M. M. (2005), Introduction to Chemical Engineering Thermodynamics (seventh ed.), New York: McGraw-Hill, p. 342, ISBN 0-07-310445-0
^ Perry, R.H.; Green, D.W., eds. (1997). Perry's Chemical Engineers' Handbook (7th ed.). McGraw-hill. ISBN 0-07-049841-5.
^ Smith, J. M.; Van Ness, H. C.; Abbott, M. M. (2005), Introduction to Chemical Engineering Thermodynamics (seventh ed.), New York: McGraw-Hill, p. 351, ISBN 0-07-310445-0

Revisions and contributors Edit on Wikipedia Read on Wikipedia

View on Grokipedia

from Grokipedia

In thermodynamics, the bubble point is the temperature at a given pressure at which the first bubble of vapor forms when heating a liquid, marking the onset of vaporization in a system that is initially entirely liquid.^[1] This condition represents equilibrium between the liquid phase and an infinitesimal amount of vapor, and for pure components, it coincides with the boiling point.^[1] For ideal multi-component mixtures, according to Raoult's law, the bubble point is the temperature where the total pressure equals the sum of the partial vapor pressures of the components in the liquid phase, expressed as

P = \sum x_i P_i^{\text{sat}}

, with

x_i

denoting the liquid mole fraction and

P_i^{\text{sat}}

the saturation vapor pressure of component

i

.^[2] In vapor-liquid equilibrium (VLE) phase diagrams, the bubble point curve outlines the boundary separating the all-liquid region from the two-phase liquid-vapor region, contrasting with the dew point curve, which marks the onset of liquid formation from vapor.^[3] This curve is essential for analyzing phase behavior in binary or multi-component systems under varying temperatures and pressures.^[3] The concept is fundamental in chemical engineering processes such as distillation, where bubble point data inform the design of separation columns, including the number of stages and reflux ratios—for instance, in azeotropic distillation of isopropanol-water mixtures using entrainers like methyl butyl ether.^[3] In petroleum engineering, the bubble point pressure defines the threshold below which dissolved gases begin to evolve from reservoir fluids, influencing production strategies, gas cap formation, and storage requirements to avoid premature vaporization.^[3] Accurate determination of bubble points, often via equations of state or experimental measurements, ensures safe and efficient handling of hydrocarbons and refrigerants in industrial applications.^[2]

Definition and Concepts

Bubble Point Temperature

The bubble point temperature of a liquid mixture is defined as the temperature at which the first bubble of vapor forms upon heating the mixture at constant pressure, marking the initiation of the boiling process for the multicomponent system.^[4] This condition represents the point where the liquid phase is in equilibrium with an infinitesimal amount of vapor, with the overall composition matching that of the liquid.^[4] At the bubble point temperature, the total vapor pressure exerted by the components in the mixture equals the prevailing system pressure, allowing the formation of the initial vapor bubble while the bulk remains liquid.^[4] This equilibrium arises from the summation of partial pressures according to principles such as Raoult's law for ideal solutions, where the vapor composition differs from the liquid due to preferential evaporation of more volatile components.^[4] For instance, in a binary mixture like ethanol-water at 1 atm, the bubble point temperature occurs around 78.2°C for pure ethanol but shifts higher with increasing water content, reflecting the interplay of component volatilities.^[5] In the case of a pure substance, the bubble point temperature is the boiling point at the given pressure, as there is no compositional variation to influence phase transition. For mixtures, however, this temperature is generally lower than the boiling point of the least volatile component, as the presence of more volatile species accelerates the onset of vaporization.^[4] Several factors govern the bubble point temperature: the mixture's composition, where increasing the mole fraction of volatile components decreases the temperature; the system pressure, which exhibits a direct relationship such that higher pressures elevate the required temperature to achieve equilibrium; and the relative volatilities of the components, which widen the temperature range over which boiling progresses in non-ideal mixtures.^[4] These elements are fundamentally tied to vapor-liquid equilibrium conditions.^[4]

Bubble Point Pressure

The bubble point pressure is defined as the pressure at which the first bubble of vapor forms from a liquid mixture upon reduction of the system pressure at constant temperature, marking the onset of vapor-liquid equilibrium for the mixture.^[6] This pressure serves as the saturation pressure, below which the liquid becomes unstable and phase separation begins, transitioning the system from a single liquid phase to a two-phase mixture.^[7] At the bubble point pressure, the physical process involves the equality between the total system pressure and the sum of the partial pressures exerted by each component in the liquid phase, based on their mole fractions and individual vapor pressures at the given temperature.^[8] For ideal mixtures, this follows from Raoult's law, where each partial pressure is the product of the liquid mole fraction and the pure component's saturation vapor pressure, leading to the initiation of infinitesimal vapor formation without significant composition change in the bulk liquid. This equilibrium condition ties into broader phase behavior principles, where the bubble point delineates the boundary of liquid stability under isothermal compression or decompression. In practical contexts, such as underground oil reservoirs, the bubble point pressure indicates the threshold below which dissolved gas evolves from the crude oil, potentially reducing oil mobility and affecting production rates; typical values for conventional reservoir oils range from 1800 to 2600 psi.^[7] For pure substances, the bubble point pressure coincides exactly with the vapor pressure at that temperature, as there are no compositional effects to consider.^[1] Several factors influence the bubble point pressure, including temperature, which generally increases the pressure due to higher volatility of components; mixture composition, where higher concentrations of lighter, more volatile species elevate the pressure; and intermolecular interactions, which alter activity coefficients and thus deviate from ideal behavior, impacting overall volatility.^[7] These influences are captured in empirical correlations like that of Standing (1947), which relates bubble point pressure to solution gas-oil ratio, gas specific gravity, reservoir temperature, and oil API gravity.^[9]

Thermodynamic Principles

Vapor-Liquid Equilibrium

Vapor-liquid equilibrium (VLE) represents the state in a system where the liquid and vapor phases coexist with unchanging compositions over time, achieved when the rate of evaporation from the liquid phase equals the rate of condensation from the vapor phase. This dynamic balance ensures that the partial pressures of components in the vapor phase remain constant, reflecting equal molecular exchange between phases./11%3A_Liquids_Solids_and_Intermolecular_Forces/11.05%3A_Vaporization_and_Vapor_Pressure) The Gibbs phase rule governs the constraints on such equilibria, stating that the degrees of freedom

F

in a system is given by

F = C - P + 2

, where

C

is the number of components and

P

is the number of phases. For a binary system (

C = 2

) at VLE (

P = 2

F = 2

, allowing specification of two intensive variables, such as temperature and liquid composition, to uniquely determine the remaining properties like pressure and vapor composition. At the bubble point condition within this framework—where the first infinitesimal vapor bubble forms in equilibrium with the bulk liquid—fixing the pressure and liquid composition (one variable for a binary mixture) determines the equilibrium temperature, effectively reducing the independent variables to align with the univariant nature of the saturation curve for that composition. At VLE, the fundamental criterion for equilibrium is the equality of chemical potentials for each component across phases, which translates to the equality of fugacities:

f_i^L = f_i^V

for component

i

, where

f_i^L

is the fugacity in the liquid phase and

f_i^V

in the vapor phase. Fugacity, analogous to pressure for ideal gases but accounting for non-ideal behavior, ensures that the escaping tendency of each component is identical in both phases, maintaining compositional stability. This condition underpins the thermodynamic consistency of VLE and directly defines the bubble point as the pressure or temperature where this equality holds for the incipient vapor phase matching the overall system pressure./06%3A_Fugacity)^[10] While many VLE analyses assume ideal gas behavior for the vapor phase to simplify calculations—treating fugacity as partial pressure—these assumptions falter at high pressures, low temperatures, or near critical points, where intermolecular forces and finite molecular volumes cause significant deviations. In such cases, real gas corrections via equations of state are essential to accurately compute fugacities and predict equilibrium states.^[11] Historically, the concept of VLE for ideal mixtures was formalized by Raoult's law, proposed by François-Marie Raoult in 1887, which posits that the partial vapor pressure of each component in an ideal solution is proportional to its mole fraction in the liquid phase. This early model laid the groundwork for understanding ideal VLE behavior and remains a cornerstone for introductory analyses, though extensions for non-ideal systems followed later.^[12]^[13]

Role in Phase Behavior

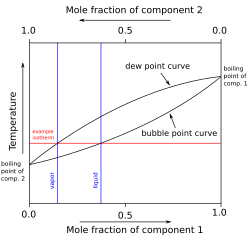
In temperature-composition (T-x-y) phase diagrams at constant pressure, the bubble point curve represents the locus of temperatures at which the first infinitesimal bubble of vapor forms from a liquid mixture of varying compositions, marking the boundary between the single-phase liquid region and the two-phase liquid-vapor region.^[14] This curve, often nonlinear for nonideal mixtures, illustrates how the boiling temperature decreases or increases with composition depending on the relative volatilities of the components, providing a visual tool for understanding the onset of vaporization in isothermal or isobaric processes.^[15] For binary systems, the bubble point curve forms the lower boundary of the two-phase envelope in T-x-y diagrams, separating the subcooled liquid region from the coexistence area where partial vaporization occurs, and it connects the boiling points of the pure components.^[15] In contrast, multicomponent systems are typically represented in pressure-temperature (P-T) space, where the bubble point appears as a line tracing the conditions under which the first vapor bubble emerges from the liquid phase, influenced by the overall composition and forming part of the phase envelope that encloses the two-phase region.^[16] Unlike binary systems, which show distinct dew and bubble curves meeting at the critical point, multicomponent behavior extends this to broader envelopes with cricondentherm and cricondenbar points, but the bubble line still delineates the liquid region's limit.^[3] The presence of azeotropes significantly alters the shape of the bubble point curve due to strong nonideal interactions between components. In systems forming minimum boiling azeotropes, such as ethanol-water, the curve exhibits a minimum temperature point where the liquid and vapor compositions coincide, causing the bubble and dew curves to touch and deviate from ideal linearity, which complicates separation processes.^[4] For maximum boiling azeotropes, like nitric acid-water, the curve instead shows a maximum temperature extremum, resulting in a peaked shape that reverses the typical volatility trend and leads to the azeotrope having a higher boiling point than either pure component.^[4] At the bubble point, the phase transition initiates vaporization, where heating a liquid mixture beyond this temperature produces an initial vapor phase enriched in the more volatile components, while the remaining liquid becomes depleted in those components, driving compositional changes across the two-phase region.^[17] This selective vaporization underpins distillation and other separation techniques, as the vapor's composition shifts progressively toward the lighter end-member with continued heating until the dew point is reached.^[17] Experimental determination of bubble points relies on techniques like ebulliometry, which measures the equilibrium temperature at which vapor bubbles first appear in a boiling liquid under controlled pressure. In a typical setup, an inclined ebulliometer with a stirrer maintains quasi-static conditions, allowing precise temperature readings for binary or multicomponent mixtures as vaporization begins, often validated against models like Raoult's law for ideal cases.^[18] This method ensures accurate data for phase diagrams by minimizing superheating and providing reproducible results across composition ranges.^[18]

Calculation Methods

For Ideal Mixtures

For ideal mixtures, the bubble point is determined under the assumption that the components obey Raoult's law, which states that the partial pressure of each component

p_i

in the vapor phase is equal to the product of its liquid mole fraction

x_i

and the saturation vapor pressure of the pure component

P_i^{\text{sat}}

, or

p_i = x_i P_i^{\text{sat}}

.^[19] This ideal behavior assumes no interactions between unlike molecules beyond simple averaging, leading to linear vapor pressure-composition relationships.^[19] The fundamental equation for the bubble point condition is the equality of the total pressure to the sum of partial pressures:

P_{\text{total}} = \sum_i x_i P_i^{\text{sat}}(T)

This equation is solved iteratively for the temperature

T

when

P_{\text{total}}

and the

x_i

are specified, as

P_i^{\text{sat}}

depends on temperature. The saturation vapor pressures

P_i^{\text{sat}}

are typically calculated using the Antoine equation:

\log_{10} P^{\text{sat}} = A - \frac{B}{T + C}

where

P^{\text{sat}}

is in bar,

T

is in K, and

A

B

C

are empirical constants specific to each component, valid over defined temperature ranges (e.g., for benzene from 287.7 to 354.1 K with

A = 4.01814

B = 1203.835

C = -53.226

; for toluene from 308.5 to 384.7 K with

A = 4.07827

B = 1343.943

C = -53.773

).^[20]^[21] The iterative procedure to find the bubble point temperature proceeds as follows:

Select an initial guess for $T$ , often between the boiling points of the pure components.
Compute $P_i^{\text{sat}}(T)$ for each component using the Antoine equation.
Calculate the sum $\sum_i x_i P_i^{\text{sat}}(T)$ and compare it to $P_{\text{total}}$ .
Adjust $T$ (increase if the sum is less than $P_{\text{total}}$ , decrease otherwise) and repeat until convergence within a specified tolerance, such as 0.1 K.^[22]

As a representative example, consider an equimolar mixture of benzene and toluene (

x_{\text{benzene}} = x_{\text{toluene}} = 0.5

) at 1 atm (760 mmHg). Using Antoine constants adjusted for mmHg units (benzene:

A = 6.893

B = 1203.93

C = 219.9

; toluene:

A = 6.958

B = 1347.0

C = 219.7

) and iterating from an initial

T = 90^\circ

C, the bubble point converges to approximately 92°C, where the summed partial pressures equal 760 mmHg.^[22] This approach is limited to mixtures where components have similar molecular sizes, shapes, and polarities—such as non-polar hydrocarbons—and applies reliably at low to moderate pressures where deviations from ideality are minimal./Equilibria/Physical_Equilibria/Raoults_Law_and_Ideal_Mixtures_of_Liquids)

For Non-Ideal Mixtures

In real mixtures, deviations from ideal behavior arise due to molecular interactions such as hydrogen bonding or polar effects, which cause the fugacity of components in the liquid phase to differ from that predicted by Raoult's law.^[23] These non-idealities are accounted for by introducing activity coefficients

\gamma_i

for each component

i

, which correct the partial pressure in the modified Raoult's law:

y_i P = x_i \gamma_i P_i^{\sat}(T)

.^[24] For bubble point calculations in non-ideal mixtures at a specified total pressure

P

, the temperature

T

is determined iteratively by solving the equation

\sum_i x_i \gamma_i(T, \mathbf{x}) P_i^{\sat}(T) = P,

where

x_i

are the known liquid mole fractions,

P_i^{\sat}(T)

is the saturation vapor pressure of pure component

i

T

, and

\gamma_i

depends on both

T

and composition

\mathbf{x}

.^[25] This requires successive approximations because

\gamma_i

and

P_i^{\sat}

are functions of

T

, often starting from an ideal estimate and refining until convergence. Activity coefficients are modeled using thermodynamic expressions fitted to experimental vapor-liquid equilibrium (VLE) data. The Wilson equation, developed in 1964, is one such local composition model given by

\ln \gamma_i = -\ln \left( x_i + \sum_{j \neq i} x_j \Lambda_{ij} \right) + \sum_k x_k \ln \left( \frac{\Lambda_{ik}}{x_i + \sum_j x_j \Lambda_{jk}} \right) + 1 - \sum_j \frac{x_j \Lambda_{ji}}{x_j + \sum_k x_k \Lambda_{kj}},

lnγi=−ln

xi+j=i∑xjΛij

+k∑xkln(xi+∑jxjΛjkΛik)+1−j∑xj+∑kxkΛkjxjΛji, with $\Lambda_{ij} = \frac{v_j}{v_i} \exp\left( -\frac{\lambda_{ij} - \lambda_{jj}}{RT} \right)$ , where $v_i$ are pure-component molar volumes and the binary parameters $\lambda_{ij}$ (and $\lambda_{ji}$ ) are regressed from binary VLE measurements.^[23] This model effectively captures both positive and negative deviations in many polar and associating systems. For systems lacking experimental data, the UNIFAC (UNIversal Functional Activity Coefficient) method predicts $\gamma_i$ via a group-contribution approach, decomposing molecules into functional groups (e.g., -CH3, -OH) and using interaction parameters between groups derived from a database of reference systems.^[24] The activity coefficient is split into a combinatorial term accounting for size and shape differences and a residual term for energetic interactions, enabling estimates for unstudied mixtures based solely on molecular structure. In multicomponent systems, solving the bubble point equation couples the activity model with vapor pressures, often requiring numerical techniques like the Newton-Raphson method to iteratively update $T$ based on the residual $\sum_i x_i \gamma_i P_i^{\sat} - P = 0$ , or successive substitution within isothermal flash algorithms that handle phase fractions and compositions.^[26] These methods ensure convergence for complex non-ideal behaviors, such as azeotropes. Consider an ethanol-water mixture forming a minimum-boiling azeotrope at approximately 89 mol% ethanol and 1 atm, where activity coefficients exceed unity ( $\gamma_{\text{ethanol}} \approx 1.2$ , $\gamma_{\text{water}} \approx 6$ ) due to positive deviations from ideality, resulting in a bubble point temperature of about 78.2°C—lower than the ideal Raoult's law prediction of around 78.5°C for the same composition, which ignores these interactions.^[27] Commercial software like Aspen Plus implements these models, including Wilson and UNIFAC, for rigorous bubble point simulations in process design, integrating thermodynamic property packages with numerical solvers.

Applications

In Distillation Processes

In distillation processes, the bubble point plays a crucial role in column design by determining the tray temperatures required for effective vapor-liquid equilibrium and separation efficiency. The bubble point temperature of the liquid on each tray establishes the conditions under which vaporization begins, ensuring optimal vapor-liquid contact that enhances mass transfer rates in fractional distillation columns.^[28] Accurate prediction of bubble points allows engineers to size trays and select internals that maintain stable operation, preventing inefficiencies from improper temperature profiles.^[29] The bubble point curve is integral to the McCabe-Thiele method for designing binary distillation separations, where it forms part of the vapor-liquid equilibrium data used to construct the diagram and estimate the number of equilibrium stages. In this graphical approach, the intersection of the q-line—derived from the feed's bubble point condition—with the equilibrium curve helps locate the feed tray and step off theoretical stages between operating lines.^[29] For feeds at the bubble point (q=1), the q-line is vertical, simplifying the analysis of stage requirements for saturated liquid feeds in systems like benzene-toluene separations.^[30] From an energy balance perspective, heating the bottoms liquid to its bubble point initiates vapor generation in the reboiler, directly influencing the reflux ratio and reboiler duty calculations essential for overall column energy optimization. The reboiler duty, often expressed as

Q_R = B V_B \Delta H_{vap}

, where

B

is the bottoms flow rate,

V_B

is the boilup ratio, and

\Delta H_{vap}

is the heat of vaporization evaluated at bubble point conditions, scales with the reflux ratio to balance separation sharpness against energy consumption.^[29] Maintaining operation near the bubble point minimizes excess heating, reducing utility costs while ensuring sufficient vapor flow for countercurrent contact.^[28] In industrial ethanol production, the bubble point of the fermentation broth (typically 5-10% ethanol by volume) guides the operation of the stripping column, where heating to this point vaporizes volatiles to concentrate the ethanol to approximately 40-50% in the overhead vapor before feeding to the rectification column to achieve ~95% purity.^[31] This step in the beer still or stripping section leverages bubble point data to control steam input and tray temperatures, achieving efficient removal of water and fusel oils in multi-column setups. Handling non-ideal mixtures presents challenges in distillation, as deviations from Raoult's law require precise bubble point predictions using activity coefficient models to avoid operational issues like tray flooding or weeping. Inaccurate predictions can lead to excessive vapor velocities causing liquid holdup and flooding, or insufficient vapor flow resulting in weeping, where liquid leaks through tray perforations and reduces separation efficiency by up to 10-20%.^[32] Advanced thermodynamic models, such as UNIQUAC, are thus employed to forecast bubble points reliably for azeotropic or close-boiling non-ideal systems.^[33]

In Reservoir Engineering

In reservoir engineering, the bubble point pressure, denoted as

P_b

, represents the pressure at which the first bubble of solution gas begins to liberate from the oil in a petroleum reservoir at reservoir temperature.^[34] This threshold marks the transition from single-phase liquid flow to the onset of gas exsolution, fundamentally altering the reservoir's phase behavior.^[35] When reservoir pressure drops below

P_b

, dissolved gas evolves, forming free gas bubbles that occupy pore space and induce changes in relative permeability. This leads to two-phase oil-gas flow, where the gas saturation reduces the relative permeability to oil, thereby decreasing oil mobility and potentially accelerating gas breakthrough at production wells.^[36] Such dynamics can lower overall oil recovery efficiency in solution-gas drive mechanisms unless mitigated by pressure support strategies. The bubble point pressure is determined through laboratory pressure-volume-temperature (PVT) analysis, specifically via constant composition expansion (CCE) experiments. In a CCE test, a reservoir fluid sample is pressurized above

P_b

and then gradually depressurized at constant temperature and composition, with relative volume measured against pressure; the deviation from linearity in the volume-pressure plot identifies

P_b

as the point where gas liberation begins.^[37] Reservoirs are classified as undersaturated or saturated based on their initial pressure relative to

P_b

. In undersaturated reservoirs, where initial reservoir pressure

P_{res} > P_b

, the oil flows as a single liquid phase until pressure depletion reaches

P_b

, after which gas evolves uniformly without initial free gas presence.^[38] Conversely, in saturated reservoirs (

P_{res} = P_b

), production immediately initiates gas liberation, often resulting in the migration of evolved gas to the structural crest to form a secondary gas cap that expands to drive oil displacement.^[39] Economically, maintaining reservoir pressure above

P_b

is critical to avoid premature gas coning and maximize recovery, typically achieved through gas injection into the aquifer or gas cap to sustain single-phase flow and enhance sweep efficiency. For instance, in North Sea fields like Alba, where

P_b

ranges from approximately 2000 to 3000 psi, such pressure management has supported recovery factors exceeding 40% by preventing early gas breakthrough.^[40]^[41] When direct PVT measurements are unavailable,

P_b

can be estimated using empirical correlations such as Standing's (1947), which relates bubble point pressure to solution gas-oil ratio, gas specific gravity, oil API gravity, and reservoir temperature:

P_b = 18.2 \left[ \left( \frac{R_{sb}}{\gamma_g} \right)^{0.83} \times 10^{0.00091 T - 0.0125 \gamma_{API}} - 1.4 \right]

where

P_b

is in psia,

R_{sb}

is the solution gas-oil ratio at the bubble point in scf/STB,

\gamma_g

is the gas specific gravity (air = 1),

\gamma_{API}

is the stock-tank oil API gravity in degrees, and

T

is the reservoir temperature in °F. This correlation, developed from California crude oil data, provides reliable estimates for undersaturated black oils with average absolute deviations around 7-10% in validation datasets.^[7]

Info Pages

Talk Pages

Special Pages

Bubble point

Recent from talks

Recent from talks

Contribute something

Contribute something

Media Pages

Timelines

Articles

Notes collections

Notes

Notes

Days in Chronicle

Bubble point

Calculating the bubble point

See also

References

Bubble point

Definition and Concepts

Bubble Point Temperature

Bubble Point Pressure

Thermodynamic Principles

Vapor-Liquid Equilibrium

Role in Phase Behavior

Calculation Methods

For Ideal Mixtures

For Non-Ideal Mixtures

Applications

In Distillation Processes

In Reservoir Engineering

References

Add your contribution

Related Hubs

Contribute something

History

Media collections

Bubble point

Recent from talks

Recent from talks

Contribute something

Contribute something

Media Pages

Timelines

Articles

Notes collections

Notes

Notes

Days in Chronicle

Bubble point

Calculating the bubble point

See also

References

Bubble point

Definition and Concepts

Bubble Point Temperature

Bubble Point Pressure

Thermodynamic Principles

Vapor-Liquid Equilibrium

Role in Phase Behavior

Calculation Methods

For Ideal Mixtures

For Non-Ideal Mixtures

Add your contribution

Related Hubs

Contribute something