Recent from talks
Contribute something
Nothing was collected or created yet.
Liquid
View on Wikipedia

| Part of a series on |
| Continuum mechanics |
|---|
Liquid is a state of matter with a definite volume but no fixed shape. When resting in a container, liquids typically adapt to the shape of the container.[note 1] Liquids are nearly incompressible, maintaining their volume even under pressure. The density of a liquid is usually close to that of a solid, and much higher than that of a gas. Liquids are a form of condensed matter alongside solids, and a form of fluid alongside gases.
A liquid is composed of atoms or molecules held together by intermolecular bonds of intermediate strength. These forces allow the particles to move around one another while remaining closely packed. In contrast, solids have particles that are tightly bound by strong intermolecular forces, limiting their movement to small vibrations in fixed positions. Gases, on the other hand, consist of widely spaced, freely moving particles with only weak intermolecular forces.
As temperature increases, the molecules in a liquid vibrate more intensely, causing the distances between them to increase. At the boiling point, the cohesive forces between the molecules are no longer sufficient to keep them together, and the liquid transitions into a gaseous state. Conversely, as temperature decreases, the distance between molecules shrinks. At the freezing point, the molecules typically arrange into a structured order in a process called crystallization, and the liquid transitions into a solid state.
Although liquid water is abundant on Earth, this state of matter is actually the least common in the known universe, because liquids require a relatively narrow temperature/pressure range to exist. Most known matter in the universe is either gaseous (as interstellar clouds) or plasma (as stars).
Examples
[edit]Only two elements are liquid at standard conditions for temperature and pressure: mercury and bromine. Four more elements have melting points slightly above room temperature: francium, caesium, gallium and rubidium.[1]
Pure substances that are liquid under normal conditions include water, ethanol and many other organic solvents. Liquid water is of vital importance in chemistry and biology, and it is necessary for all known forms of life.[2][3] Inorganic liquids in this category include inorganic nonaqueous solvents and many acids.
Mixtures that are liquid at room temperature include alloys such as galinstan (a gallium-indium-tin alloy that melts at −19 °C or −2 °F) and some amalgams (alloys involving mercury).[4] Certain mixtures, such as the sodium-potassium metal alloy NaK, are liquid at room temperature even though the individual elements are solid under the same conditions (see eutectic mixture).[5] Everyday liquid mixtures include aqueous solutions like household bleach, other mixtures of different substances such as mineral oil and gasoline, emulsions like vinaigrette or mayonnaise, suspensions like blood, and colloids like paint and milk.
Many gases can be liquefied by cooling, producing liquids such as liquid oxygen, liquid nitrogen, liquid hydrogen and liquid helium. However, not all gases can be liquefied at atmospheric pressure. Carbon dioxide, for example, solidifies directly into dry ice rather than becoming a liquid, and it can only be liquified at pressures above 5.1 atm.[6] Most liquids solidify as the temperature is decreased further. Liquid helium is exceptional in that it does not become solid even at absolute zero (0 K) under standard pressure due to its quantum properties.[7]
Properties
[edit]Volume
[edit]
Quantities of liquids are measured in units of volume. These include the SI unit cubic metre (m3) and its divisions, in particular the cubic decimeter, more commonly called the litre (1 dm3 = 1 L = 0.001 m3), and the cubic centimetre, also called millilitre (1 cm3 = 1 mL = 0.001 L = 10−6 m3).[8]
The volume of a quantity of liquid is fixed by its temperature and pressure. Liquids generally expand when heated, and contract when cooled. Water between 0 °C and 4 °C is a notable exception.[9]
On the other hand, liquids have little compressibility. Water, for example, will compress by only 46.4 parts per million for every unit increase in atmospheric pressure (bar).[10] At around 4000 bar (400 megapascals or 58,000 psi) of pressure at room temperature water experiences only an 11% decrease in volume.[11] Incompressibility makes liquids suitable for transmitting hydraulic power, because a change in pressure at one point in a liquid is transmitted undiminished to every other part of the liquid and very little energy is lost in the form of compression.[12]
However, the negligible compressibility does lead to other phenomena. The banging of pipes, called water hammer, occurs when a valve is suddenly closed, creating a huge pressure-spike at the valve that travels backward through the system at just under the speed of sound. Another phenomenon caused by liquid's incompressibility is cavitation. Because liquids have little elasticity they can literally be pulled apart in areas of high turbulence or dramatic change in direction, such as the trailing edge of a boat propeller or a sharp corner in a pipe. A liquid in an area of low pressure (vacuum) vaporizes and forms bubbles, which then collapse as they enter high pressure areas. This causes liquid to fill the cavities left by the bubbles with tremendous localized force, eroding any adjacent solid surface.[13]
Pressure and buoyancy
[edit]In a gravitational field, liquids exert pressure on the sides of a container as well as on anything within the liquid itself. This pressure is transmitted in all directions and increases with depth. If a liquid is at rest in a uniform gravitational field, the pressure at depth is given by[14]
where:
- is the pressure at the surface
- is the density of the liquid, assumed uniform with depth
- is the gravitational acceleration
For a body of water open to the air, would be the atmospheric pressure.
Static liquids in uniform gravitational fields also exhibit the phenomenon of buoyancy, where objects immersed in the liquid experience a net force due to the pressure variation with depth. The magnitude of the force is equal to the weight of the liquid displaced by the object, and the direction of the force depends on the average density of the immersed object. If the density is smaller than that of the liquid, the buoyant force points upward and the object floats, whereas if the density is larger, the buoyant force points downward and the object sinks. This is known as Archimedes' principle.[15]
Surfaces
[edit]
Unless the volume of a liquid exactly matches the volume of its container, one or more surfaces are observed. The presence of a surface introduces new phenomena which are not present in a bulk liquid. This is because a molecule at a surface possesses bonds with other liquid molecules only on the inner side of the surface, which implies a net force pulling surface molecules inward. Equivalently, this force can be described in terms of energy: there is a fixed amount of energy associated with forming a surface of a given area. This quantity is a material property called the surface tension, in units of energy per unit area (SI units: J/m2). Liquids with strong intermolecular forces tend to have large surface tensions.[16]
A practical implication of surface tension is that liquids tend to minimize their surface area, forming spherical drops and bubbles unless other constraints are present. Surface tension is responsible for a range of other phenomena as well, including surface waves, capillary action, wetting, and ripples. In liquids under nanoscale confinement, surface effects can play a dominating role since – compared with a macroscopic sample of liquid – a much greater fraction of molecules are located near a surface.
The surface tension of a liquid directly affects its wettability. Most common liquids have tensions ranging in the tens of mJ/m2, so droplets of oil, water, or glue can easily merge and adhere to other surfaces, whereas liquid metals such as mercury may have tensions ranging in the hundreds of mJ/m2, thus droplets do not combine easily and surfaces may only wet under specific conditions.
The surface tensions of common liquids occupy a relatively narrow range of values when exposed to changing conditions such as temperature, which contrasts strongly with the enormous variation seen in other mechanical properties, such as viscosity.[17]
Flow
[edit]
An important physical property characterizing the flow of liquids is viscosity. Intuitively, viscosity describes the resistance of a liquid to flow. More technically, viscosity measures the resistance of a liquid to deformation at a given rate, such as when it is being sheared at finite velocity.[18] A specific example is a liquid flowing through a pipe: in this case the liquid undergoes shear deformation since it flows more slowly near the walls of the pipe than near the center. As a result, it exhibits viscous resistance to flow. In order to maintain flow, an external force must be applied, such as a pressure difference between the ends of the pipe.
The viscosity of liquids decreases with increasing temperature.[19]
Precise control of viscosity is important in many applications, particularly the lubrication industry. One way to achieve such control is by blending two or more liquids of differing viscosities in precise ratios.[20] In addition, various additives exist which can modulate the temperature-dependence of the viscosity of lubricating oils. This capability is important since machinery often operate over a range of temperatures (see also viscosity index).[21]
The viscous behavior of a liquid can be either Newtonian or non-Newtonian. A Newtonian liquid exhibits a linear strain/stress curve, meaning its viscosity is independent of time, shear rate, or shear-rate history. Examples of Newtonian liquids include water, glycerin, motor oil, honey, or mercury. A non-Newtonian liquid is one where the viscosity is not independent of these factors and either thickens (increases in viscosity) or thins (decreases in viscosity) under shear. Examples of non-Newtonian liquids include ketchup, custard, or starch solutions.[22]
Sound propagation
[edit]The speed of sound in a liquid is given by where is the bulk modulus of the liquid and the density. As an example, water has a bulk modulus of about 2.2 GPa and a density of 1000 kg/m3, which gives c = 1.5 km/s.[23]
Microscopic structure
[edit]The microscopic structure of liquids is complex and historically has been the subject of intense research and debate.[24][25][26][27] Liquids consist of a dense, disordered packing of molecules. This contrasts with the other two common phases of matter, gases and solids. Although gases are disordered, the molecules are well-separated in space and interact primarily through molecule-molecule collisions. Conversely, although the molecules in solids are densely packed, they usually fall into a regular structure, such as a crystalline lattice (glasses are a notable exception).
Short-range ordering
[edit]
While liquids do not exhibit long-range ordering as in a crystalline lattice, they do possess short-range order, which persists over a few molecular diameters.[28][29]
In all liquids, excluded volume interactions induce short-range order in molecular positions (center-of-mass coordinates). Classical monatomic liquids like argon and krypton are the simplest examples. Such liquids can be modeled as disordered "heaps" of closely packed spheres, and the short-range order corresponds to the fact that nearest and next-nearest neighbors in a packing of spheres tend to be separated by integer multiples of the diameter.[30][31]
In most liquids, molecules are not spheres, and intermolecular forces possess a directionality, i.e., they depend on the relative orientation of molecules. As a result, there is short-ranged orientational order in addition to the positional order mentioned above. Orientational order is especially important in hydrogen-bonded liquids like water.[32][33] The strength and directional nature of hydrogen bonds drives the formation of local "networks" or "clusters" of molecules. Due to the relative importance of thermal fluctuations in liquids (compared with solids), these structures are highly dynamic, continuously deforming, breaking, and reforming.[30][32]
While ordinary liquids lack long-range order, some materials exhibit intermediate behavior. Liquid crystals, for example, flow like liquids but exhibit long-range orientational alignment of their molecules. Unlike solids, they lack long-range translational order, yet their anisotropic properties set them apart from conventional liquids. As a result, liquid crystals are considered a distinct state of matter. They are utilized in technologies such as liquid-crystal displays (LCDs).[34]
Energy and entropy
[edit]The microscopic features of liquids derive from an interplay between attractive intermolecular forces and entropic forces.[35]
The attractive forces tend to pull molecules close together, and along with short-range repulsive interactions, they are the dominant forces behind the regular structure of solids. The entropic forces are not "forces" in the mechanical sense; rather, they describe the tendency of a system to maximize its entropy at fixed energy (see microcanonical ensemble). Roughly speaking, entropic forces drive molecules apart from each other, maximizing the volume they occupy. Entropic forces dominant in gases and explain the tendency of gases to fill their containers. In liquids, by contrast, the intermolecular and entropic forces are comparable, so it is not possible to neglect one in favor of the other. Quantitatively, the binding energy between adjacent molecules is the same order of magnitude as the thermal energy .[36]
No small parameter
[edit]The competition between energy and entropy makes liquids difficult to model at the molecular level, as there is no idealized "reference state" that can serve as a starting point for tractable theoretical descriptions. Mathematically, there is no small parameter from which one can develop a systematic perturbation theory.[25] This situation contrasts with both gases and solids. For gases, the reference state is the ideal gas, and the density can be used as a small parameter to construct a theory of real (nonideal) gases (see virial expansion).[37] For crystalline solids, the reference state is a perfect crystalline lattice, and possible small parameters are thermal motions and lattice defects.[32]
Role of quantum mechanics
[edit]Like all known forms of matter, liquids are fundamentally quantum mechanical. However, under standard conditions (near room temperature and pressure), much of the macroscopic behavior of liquids can be understood in terms of classical mechanics.[36][38] The "classical picture" posits that the constituent molecules are discrete entities that interact through intermolecular forces according to Newton's laws of motion. As a result, their macroscopic properties can be described using classical statistical mechanics. While the intermolecular force law technically derives from quantum mechanics, it is usually understood as a model input to classical theory, obtained either from a fit to experimental data or from the classical limit of a quantum mechanical description.[39][28] An illustrative, though highly simplified example is a collection of spherical molecules interacting through a Lennard-Jones potential.[36]
| Liquid | Temperature (K) | (nm) | |
|---|---|---|---|
| Hydrogen (H2) | 14.1 | 0.33 | 0.97 |
| Neon | 24.5 | 0.078 | 0.26 |
| Krypton | 116 | 0.018 | 0.046 |
| Carbon tetrachloride (CCl4) | 250 | 0.009 | 0.017 |
For the classical limit to apply, a necessary condition is that the thermal de Broglie wavelength,
is small compared with the length scale under consideration.[36][40] Here, is the Planck constant and is the molecule's mass. Typical values of are about 0.01-0.1 nanometers (Table 1). Hence, a high-resolution model of liquid structure at the nanoscale may require quantum mechanical considerations. A notable example is hydrogen bonding in associated liquids like water,[41][42] where, due to the small mass of the proton, inherently quantum effects such as zero-point motion and tunneling are important.[43]
For a liquid to behave classically at the macroscopic level, must be small compared with the average distance between molecules.[36] That is,
Representative values of this ratio for a few liquids are given in Table 1. The conclusion is that quantum effects are important for liquids at low temperatures and with small molecular mass.[36][38] For dynamic processes, there is an additional timescale constraint:
where is the timescale of the process under consideration. For room-temperature liquids, the right-hand side is about 10−14 seconds, which generally means that time-dependent processes involving translational motion can be described classically.[36]
At extremely low temperatures, even the macroscopic behavior of certain liquids deviates from classical mechanics. Notable examples are hydrogen and helium. Due to their low temperature and mass, such liquids have a thermal de Broglie wavelength comparable to the average distance between molecules.[36]
Dynamic phenomena
[edit]The expression for the sound velocity of a liquid,
- ,
contains the bulk modulus K. If K is frequency-independent, then the liquid behaves as a linear medium, so that sound propagates without dissipation or mode coupling. In reality, all liquids show some dispersion: with increasing frequency, K crosses over from the low-frequency, liquid-like limit to the high-frequency, solid-like limit . In normal liquids, most of this crossover takes place at frequencies between GHz and THz, sometimes called hypersound.
At sub-GHz frequencies, a normal liquid cannot sustain shear waves: the zero-frequency limit of the shear modulus is 0. This is sometimes seen as the defining property of a liquid.[44][45] However, like the bulk modulus K, the shear modulus G is also frequency-dependent and exhibits a similar crossover at hypersound frequencies.
According to linear response theory, the Fourier transform of K or G describes how the system returns to equilibrium after an external perturbation; for this reason, the dispersion step in the GHz to THz region is also called relaxation. As a liquid is supercooled toward the glass transition, the structural relaxation time exponentially increases, which explains the viscoelastic behavior of glass-forming liquids.

Experimental methods
[edit]The absence of long-range order in liquids is mirrored by the absence of Bragg peaks in X-ray and neutron diffraction. Under normal conditions, the diffraction pattern has circular symmetry, expressing the isotropy of the liquid. Radially, the diffraction intensity smoothly oscillates. This can be described by the static structure factor , with wavenumber given by the wavelength of the probe (photon or neutron) and the Bragg angle . The oscillations of express the short-range order of the liquid, i.e., the correlations between a molecule and "shells" of nearest neighbors, next-nearest neighbors, and so on.
An equivalent representation of these correlations is the radial distribution function , which is related to the Fourier transform of .[30] It represents a spatial average of a temporal snapshot of pair correlations in the liquid.
Phase transitions
[edit]
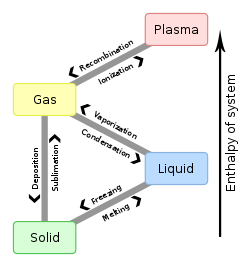
At a temperature below the boiling point, any matter in liquid form will evaporate until reaching equilibrium with the reverse process of condensation of its vapor. At this point the vapor will condense at the same rate as the liquid evaporates. Thus, a liquid cannot exist permanently if the evaporated liquid is continually removed.[46] A liquid at or above its boiling point will normally boil, though superheating can prevent this in certain circumstances.
At a temperature below the freezing point, a liquid will tend to crystallize, changing to its solid form. Unlike the transition to gas, there is no equilibrium at this transition under constant pressure,[citation needed] so unless supercooling occurs, the liquid will eventually completely crystallize. However, this is only true under constant pressure, so that (for example) water and ice in a closed, strong container might reach an equilibrium where both phases coexist. For the opposite transition from solid to liquid, see melting.
The phase diagram explains why liquids do not exist in space or any other vacuum. Since the pressure is essentially zero (except on surfaces or interiors of planets and moons) water and other liquids exposed to space will either immediately boil or freeze depending on the temperature. In regions of space near the Earth, water will freeze if the sun is not shining directly on it and vaporize (sublime) as soon as it is in sunlight. If water exists as ice on the Moon, it can only exist in shadowed holes where the sun never shines and where the surrounding rock does not heat it up too much. At some point near the orbit of Saturn, the light from the Sun is too faint to sublime ice to water vapor. This is evident from the longevity of the ice that composes Saturn's rings.[47]
Solutions
[edit]Liquids can form solutions with gases, solids, and other liquids.
Two liquids are said to be miscible if they can form a solution in any proportion; otherwise they are immiscible. As an example, water and ethanol (drinking alcohol) are miscible whereas water and gasoline are immiscible.[48] In some cases a mixture of otherwise immiscible liquids can be stabilized to form an emulsion, where one liquid is dispersed throughout the other as microscopic droplets. Usually this requires the presence of a surfactant in order to stabilize the droplets. A familiar example of an emulsion is mayonnaise, which consists of a mixture of water and oil that is stabilized by lecithin, a substance found in egg yolks.[49]
Applications
[edit]
Lubrication
[edit]Liquids are useful as lubricants due to their ability to form a thin, freely flowing layer between solid materials. Lubricants such as oil are chosen for viscosity and flow characteristics that are suitable throughout the operating temperature range of the component. Oils are often used in engines, gear boxes, metalworking, and hydraulic systems for their good lubrication properties.[50]
Solvation
[edit]Many liquids are used as solvents, to dissolve other liquids or solids. Solutions are found in a wide variety of applications, including paints, sealants, and adhesives. Naphtha and acetone are used frequently in industry to clean oil, grease, and tar from parts and machinery. Body fluids are water-based solutions.
Surfactants are commonly found in soaps and detergents. Solvents like alcohol are often used as antimicrobials. They are found in cosmetics, inks, and liquid dye lasers. They are used in the food industry, in processes such as the extraction of vegetable oil.[51]
Cooling
[edit]Liquids tend to have better thermal conductivity than gases, and the ability to flow makes a liquid suitable for removing excess heat from mechanical components. The heat can be removed by channeling the liquid through a heat exchanger, such as a radiator, or the heat can be removed with the liquid during evaporation.[52] Water or glycol coolants are used to keep engines from overheating.[53] The coolants used in nuclear reactors include water or liquid metals, such as sodium or bismuth.[54] Liquid propellant films are used to cool the thrust chambers of rockets.[55] In machining, water and oils are used to remove the excess heat generated, which can quickly ruin both the work piece and the tooling. During perspiration, sweat removes heat from the human body by evaporating. In the heating, ventilation, and air-conditioning industry (HVAC), liquids such as water are used to transfer heat from one area to another.[56]
Cooking
[edit]Liquids are often used in cooking due to their excellent heat-transfer capabilities. In addition to thermal conduction, liquids transmit energy by convection. In particular, because warmer fluids expand and rise while cooler areas contract and sink, liquids with low kinematic viscosity tend to transfer heat through convection at a fairly constant temperature, making a liquid suitable for blanching, boiling, or frying. Even higher rates of heat transfer can be achieved by condensing a gas into a liquid. At the liquid's boiling point, all of the heat energy is used to cause the phase change from a liquid to a gas, without an accompanying increase in temperature, and is stored as chemical potential energy. When the gas condenses back into a liquid this excess heat-energy is released at a constant temperature. This phenomenon is used in processes such as steaming.
Distillation
[edit]Since liquids often have different boiling points, mixtures or solutions of liquids or gases can typically be separated by distillation, using heat, cold, vacuum, pressure, or other means. Distillation can be found in everything from the production of alcoholic beverages, to oil refineries, to the cryogenic distillation of gases such as argon, oxygen, nitrogen, neon, or xenon by liquefaction (cooling them below their individual boiling points).[57]
Hydraulics
[edit]Liquid is the primary component of hydraulic systems, which take advantage of Pascal's law to provide fluid power. Devices such as pumps and waterwheels have been used to change liquid motion into mechanical work since ancient times. Oils are forced through hydraulic pumps, which transmit this force to hydraulic cylinders. Hydraulics can be found in many applications, such as automotive brakes and transmissions, heavy equipment, and airplane control systems. Various hydraulic presses are used extensively in repair and manufacturing, for lifting, pressing, clamping and forming.[58]
Liquid metals
[edit]Liquid metals have several properties that are useful in sensing and actuation, particularly their electrical conductivity and ability to transmit forces (incompressibility). As freely flowing substances, liquid metals retain these bulk properties even under extreme deformation. For this reason, they have been proposed for use in soft robots and wearable healthcare devices, which must be able to operate under repeated deformation.[59][60] The metal gallium is considered to be a promising candidate for these applications as it is a liquid near room temperature, has low toxicity, and evaporates slowly.[61]
Miscellaneous
[edit]Liquids are sometimes used in measuring devices. A thermometer often uses the thermal expansion of liquids, such as mercury, combined with their ability to flow to indicate temperature. A manometer uses the weight of the liquid to indicate air pressure.[62]
The free surface of a rotating liquid forms a circular paraboloid and can therefore be used as a telescope. These are known as liquid-mirror telescopes.[63] They are significantly cheaper than conventional telescopes,[64] but can only point straight upward (zenith telescope). A common choice for the liquid is mercury.[citation needed]
Prediction of liquid properties
[edit]Methods for predicting liquid properties can be organized by their "scale" of description, that is, the length scales and time scales over which they apply.[65][66]
- Macroscopic methods use equations that directly model the large-scale behavior of liquids, such as their thermodynamic properties and flow behavior.
- Microscopic methods use equations that model the dynamics of individual molecules.
- Mesoscopic methods fall in between, combining elements of both continuum and particle-based models.
Macroscopic
[edit]Empirical correlations
[edit]Empirical correlations are simple mathematical expressions intended to approximate a liquid's properties over a range of experimental conditions, such as varying temperature and pressure.[67] They are constructed by fitting simple functional forms to experimental data. For example, the temperature-dependence of liquid viscosity is sometimes approximated by the function , where and are fitting constants.[68] Empirical correlations allow for extremely efficient estimates of physical properties, which can be useful in thermophysical simulations. However, they require high quality experimental data to obtain a good fit and cannot reliably extrapolate beyond the conditions covered by experiments.
Thermodynamic potentials
[edit]Thermodynamic potentials are functions that characterize the equilibrium state of a substance. An example is the Gibbs free energy , which is a function of pressure and temperature. Knowing any one thermodynamic potential is sufficient to compute all equilibrium properties of a substance, often simply by taking derivatives of .[37] Thus, a single correlation for can replace separate correlations for individual properties.[69][70] Conversely, a variety of experimental measurements (e.g., density, heat capacity, vapor pressure) can be incorporated into the same fit; in principle, this would allow one to predict hard-to-measure properties like heat capacity in terms of other, more readily available measurements (e.g., vapor pressure).[71]
Hydrodynamics
[edit]Hydrodynamic theories describe liquids in terms of space- and time-dependent macroscopic fields, such as density, velocity, and temperature. These fields obey partial differential equations, which can be linear or nonlinear.[72] Hydrodynamic theories are more general than equilibrium thermodynamic descriptions, which assume that liquids are approximately homogeneous and time-independent. The Navier-Stokes equations are a well-known example: they are partial differential equations giving the time evolution of density, velocity, and temperature of a viscous fluid. There are numerous methods for numerically solving the Navier-Stokes equations and its variants.[73][74]
Mesoscopic
[edit]Mesoscopic methods operate on length and time scales between the particle and continuum levels. For this reason, they combine elements of particle-based dynamics and continuum hydrodynamics.[65]
An example is the lattice Boltzmann method, which models a fluid as a collection of fictitious particles that exist on a lattice.[65] The particles evolve in time through streaming (straight-line motion) and collisions. Conceptually, it is based on the Boltzmann equation for dilute gases, where the dynamics of a molecule consists of free motion interrupted by discrete binary collisions, but it is also applied to liquids. Despite the analogy with individual molecular trajectories, it is a coarse-grained description that typically operates on length and time scales larger than those of true molecular dynamics (hence the notion of "fictitious" particles).
Other methods that combine elements of continuum and particle-level dynamics include smoothed-particle hydrodynamics,[75][76] dissipative particle dynamics,[77] and multiparticle collision dynamics.[78]
Microscopic
[edit]Microscopic simulation methods work directly with the equations of motion (classical or quantum) of the constituent molecules.
Classical molecular dynamics
[edit]Classical molecular dynamics (MD) simulates liquids using Newton's law of motion; from Newton's second law (), the trajectories of molecules can be traced out explicitly and used to compute macroscopic liquid properties like density or viscosity. However, classical MD requires expressions for the intermolecular forces ("F" in Newton's second law). Usually, these must be approximated using experimental data or some other input.[28]
Ab initio (quantum) molecular dynamics
[edit]Ab initio quantum mechanical methods simulate liquids using only the laws of quantum mechanics and fundamental atomic constants.[39] In contrast with classical molecular dynamics, the intermolecular force fields are an output of the calculation, rather than an input based on experimental measurements or other considerations. In principle, ab initio methods can simulate the properties of a given liquid without any prior experimental data. However, they are very expensive computationally, especially for large molecules with internal structure.
See also
[edit]Notes
[edit]- ^ There is no fundamental principle requiring a liquid to conform to the shape of some container. If-and-when it does conform, it's because of fundamental principles such as balance of forces and the tendency of a fluid to yield to shear stress. The liquid remains a liquid even if it has no container at all, such as: droplets of water suspended in a cloud, a puddle of water on a flat tabletop, a stream of water from a fountain or pitcher, the oceans of a large watery planet, and so on. See also ullage motor.
References
[edit]- ^ Gray, Theodore; Mann, Nick (2012). The elements: a visual exploration of every known atom in the universe (1st paperback ed.). New York: Black Dog & Leventhal. p. 127. ISBN 978-1-57912-814-2.
- ^ Mottl, Michael J.; Glazer, Brian T.; Kaiser, Ralf I.; Meech, Karen J. (December 2007). "Water and astrobiology" (PDF). Geochemistry. 67 (4): 253–282. Bibcode:2007ChEG...67..253M. doi:10.1016/j.chemer.2007.09.002. ISSN 0009-2819.
- ^ Chyba, Christopher F.; Hand, Kevin P. (1 September 2005). "Astrobiology: The Study of the Living Universe". Annual Review of Astronomy and Astrophysics. 43 (1): 31–74. Bibcode:2005ARA&A..43...31C. doi:10.1146/annurev.astro.43.051804.102202. eISSN 1545-4282. ISSN 0066-4146.
- ^ Surmann, Peter; Zeyat, Hanan (2005-10-15). "Voltammetric analysis using a self-renewable non-mercury electrode". Analytical and Bioanalytical Chemistry. 383 (6). Springer Science and Business Media LLC: 1009–1013. doi:10.1007/s00216-005-0069-7. ISSN 1618-2642. PMID 16228199. S2CID 22732411.
- ^ Leonchuk, Sergei S.; Falchevskaya, Aleksandra S.; Nikolaev, Vitaly; Vinogradov, Vladimir V. (2022). "NaK alloy: underrated liquid metal". Journal of Materials Chemistry A. 10 (43). Royal Society of Chemistry (RSC): 22955–22976. doi:10.1039/d2ta06882f. ISSN 2050-7488. S2CID 252979251.
- ^ Silberberg 2009, pp. 448–449.
- ^ Wilks, J. (1967). The Properties of Liquid and Solid Helium. Oxford: Clarendon Press. p. 1. ISBN 0-19-851245-7.
- ^ Knight, Randall D. (2008). Physics for Scientists and Engineers: A Strategic Approach (With Modern Physics). Addison-Wesley. p. 443. ISBN 978-0-8053-2736-6.
- ^ Silberberg, Martin S. (2009). Chemistry: The Molecular Nature of Matter and Change. McGraw-Hill Higher Education. p. 461. ISBN 978-0-07-304859-8.
- ^ "Compressibility of Liquids". hyperphysics.phy-astr.gsu.edu. Archived from the original on 7 December 2017. Retrieved 8 May 2018.
- ^ Zhang, Wenwu (2011). Intelligent Energy Field Manufacturing: Interdisciplinary Process Innovations. CRC Press. p. 144.
- ^ Knight 2008, p. 454.
- ^ Gupta, S. C. (2006). Fluid Mechanics and Hydraulic Machines. Dorling-Kindersley. p. 85.
- ^ Knight 2008, p. 448.
- ^ Knight 2008, pp. 455–459.
- ^ Silberberg 2009, p. 457.
- ^ Edward Yu. Bormashenko (5 November 2018). Wetting of Real Surfaces. De Gruyter. pp. 3–5. ISBN 978-3-11-058314-4.
- ^ Landau, L.D.; Lifshitz, E.M. (1987). Fluid Mechanics (2nd ed.). Pergamon Press. pp. 44–45. ISBN 978-0-08-033933-7.
- ^ Bird, R. Byron; Stewart, Warren E.; Lightfoot, Edwin N. (2007). Transport Phenomena (2nd ed.). John Wiley & Sons, Inc. p. 21. ISBN 978-0-470-11539-8.
- ^ Zhmud, Boris (2014), "Viscosity Blending Equations" (PDF), Lube-Tech, 93
- ^ "Viscosity Index". UK: Anton Paar. Archived from the original on March 9, 2020. Retrieved 29 August 2018.
- ^ Boukraa, Laid (2014). Honey in Traditional and Modern Medicine. CRC Press. pp. 22–24.
- ^ Taylor, John R. (2005). Classical Mechanics. University Science Books. pp. 727–729. ISBN 978-1-891389-22-1.
- ^ Chandler, David (2017-05-05). "From 50 Years Ago, the Birth of Modern Liquid-State Science". Annual Review of Physical Chemistry. 68 (1). Annual Reviews: 19–38. arXiv:1609.04837. Bibcode:2017ARPC...68...19C. doi:10.1146/annurev-physchem-052516-044941. ISSN 0066-426X. PMID 28375691. S2CID 37248336.
- ^ a b Trachenko, K; Brazhkin, V V (2015-12-22). "Collective modes and thermodynamics of the liquid state". Reports on Progress in Physics. 79 (1) 016502. IOP Publishing. arXiv:1512.06592. doi:10.1088/0034-4885/79/1/016502. ISSN 0034-4885. PMID 26696098. S2CID 42203015.
- ^ Ben-Naim, Arieh (2009). Molecular theory of water and aqueous solutions. Part 1, Understanding water. Singapore: World Scientific. ISBN 978-981-283-761-5. OCLC 696342117.
- ^ Pothoczki, Szilvia; Temleitner, László; Pusztai, László (2015-12-01). "Structure of Neat Liquids Consisting of (Perfect and Nearly) Tetrahedral Molecules". Chemical Reviews. 115 (24). American Chemical Society (ACS): 13308–13361. doi:10.1021/acs.chemrev.5b00308. ISSN 0009-2665. PMID 26624528.
- ^ a b c Maitland, Geoffrey C.; Rigby, Maurice; Smith, E. Brian; Wakeham, W. A. (1981). Intermolecular forces: their origin and determination. Oxford: Oxford University Press. ISBN 0-19-855611-X. OCLC 8139179.
- ^ Gallo, Paola; Rovere, Mauro (2021). Physics of liquid matter. Cham: Springer. ISBN 978-3-030-68349-8. OCLC 1259588062.
- ^ a b c Chandler, David (1987). Introduction to modern statistical mechanics. New York: Oxford University Press. ISBN 0-19-504276-X. OCLC 13946448.
- ^ Finney, John L. (2013-02-22). "Bernal's road to random packing and the structure of liquids". Philosophical Magazine. 93 (31–33). Informa UK Limited: 3940–3969. Bibcode:2013PMag...93.3940F. doi:10.1080/14786435.2013.770179. ISSN 1478-6435. S2CID 55689631.
- ^ a b c Finney, J. L. (2015). Water: a very short introduction. Oxford, United Kingdom: Oxford University Press. pp. 48–52. ISBN 978-0-19-870872-8. OCLC 914537747.
- ^ Ludwig, Ralf (2005-07-11). "The Structure of Liquid Methanol". ChemPhysChem. 6 (7). Wiley: 1369–1375. doi:10.1002/cphc.200400663. ISSN 1439-4235. PMID 15991270.
- ^ Andrienko, Denis (October 2018). "Introduction to liquid crystals". Journal of Molecular Liquids. 267: 520–541. doi:10.1016/j.molliq.2018.01.175. ISSN 0167-7322.
- ^ Chandler, David (2009-09-08). "Liquids: Condensed, disordered, and sometimes complex". Proceedings of the National Academy of Sciences. 106 (36): 15111–15112. doi:10.1073/pnas.0908029106. ISSN 0027-8424. PMC 2741213. PMID 19805248.
- ^ a b c d e f g h i Hansen, Jean-Pierre; McDonald, Ian R. (2013). Theory of simple liquids: with applications to soft matter. Amsterdam: Academic Press. ISBN 978-0-12-387033-9. OCLC 855895733.
- ^ a b Kardar, Mehran (2007). Statistical physics of particles. New York, NY: Cambridge University Press. p. 130. ISBN 978-0-521-87342-0. OCLC 148639922.
- ^ a b Gray, C. G.; Gubbins, Keith E.; Joslin, C. G. (1984–2011). Theory of molecular fluids. Oxford: Oxford University Press. ISBN 0-19-855602-0. OCLC 10145548.
- ^ a b Marx, Dominik; Hutter, Jürg (2012). Ab initio molecular dynamics: basic theory and advanced methods. Cambridge: Cambridge University Press. ISBN 978-0-521-89863-8. OCLC 869135580.
- ^ Fisher, I.Z. (1964), Statistical Theory of Liquids, The University of Chicago Press
- ^ Ceriotti, Michele; Cuny, Jérôme; Parrinello, Michele; Manolopoulos, David E. (2013-09-06). "Nuclear quantum effects and hydrogen bond fluctuations in water". Proceedings of the National Academy of Sciences. 110 (39): 15591–15596. Bibcode:2013PNAS..11015591C. doi:10.1073/pnas.1308560110. ISSN 0027-8424. PMC 3785726. PMID 24014589.
- ^ Markland, Thomas E.; Ceriotti, Michele (2018-02-28). "Nuclear quantum effects enter the mainstream". Nature Reviews Chemistry. 2 (3) 0109. Springer Science and Business Media LLC. arXiv:1803.01037. doi:10.1038/s41570-017-0109. ISSN 2397-3358. S2CID 4938804.
- ^ Li, Xin-Zheng; Walker, Brent; Michaelides, Angelos (2011-04-04). "Quantum nature of the hydrogen bond". Proceedings of the National Academy of Sciences. 108 (16): 6369–6373. Bibcode:2011PNAS..108.6369L. doi:10.1073/pnas.1016653108. ISSN 0027-8424. PMC 3081025.
- ^ Born, Max (1940). "On the stability of crystal lattices". Mathematical Proceedings of the Cambridge Philosophical Society. 36 (2): 160–172. Bibcode:1940PCPS...36..160B. doi:10.1017/S0305004100017138. S2CID 104272002.
- ^ Born, Max (1939). "Thermodynamics of Crystals and Melting". Journal of Chemical Physics. 7 (8): 591–604. Bibcode:1939JChPh...7..591B. doi:10.1063/1.1750497. Archived from the original on 2016-05-15.
- ^ March, N.H.; Tosi, M.P. (2002). Introduction to Liquid State Physics. World Scientific. p. 7. Bibcode:2002ilsp.book.....M. doi:10.1142/4717. ISBN 978-981-3102-53-8.
- ^ Siegel, Ethan (2014-12-11). "Does water freeze or boil in space?". Starts With A Bang!. Retrieved 2022-02-10.
- ^ Silberberg 2009, pp. 188 and 502.
- ^ Miodownik, Mark (2019). Liquid rules: The Delightful and Dangerous Substances that Flow Through Our Lives. Houghton Mifflin Harcourt. p. 124. ISBN 978-0-544-85019-4.
- ^ Mang, Theo; Dresel, Wilfried (2007). Lubricants and Lubrication. John Wiley & Sons. ISBN 978-3-527-61033-4.
- ^ Wypych, George (2001). Handbook of Solvents. ChemTec Publishing. pp. 847–881. ISBN 978-1-895198-24-9.
- ^ Handbook of thermal conductivity of liquids and gases. Boca Raton Ann Arbor London [etc.]: CRC press. 1994. ISBN 978-0-8493-9345-7.
- ^ Erjavec, Jack (2005). Automotive Technology: A Systems Approach. Thomson/Delmar Learning. p. 309. ISBN 978-1-4018-4831-6.
- ^ Wendt, Gerald (1957). The prospects of nuclear power and technology. D. Van Nostrand Company. p. 266.
- ^ Huzel, Dieter K.; Huang, David H. (2000). Modern Engineering for Design of Liquid-Propellant Rocket Engines. Progress in Astronautics and Aeronautics. Reston: American Institute of Aeronautics and Astronautics. p. 99. ISBN 978-1-56347-013-4.
- ^ Mull, Thomas E. (1998). HVAC principles and applications manual. New York: McGraw-Hill. ISBN 978-0-07-044451-5.
- ^ Earle, R. L. (1983). Unit operations in food processing. Oxford: Pergamon Press. pp. 56–62, 138–141. ISBN 0-08-025537-X. OCLC 8451210.
- ^ Mobley, R. Keith (1999). Fluid Power Dynamics. Elsevier. p. vii. ISBN 978-0-08-050662-3.
- ^ Dickey, Michael D. (2017-04-18). "Stretchable and Soft Electronics using Liquid Metals". Advanced Materials. 29 (27) 1606425. Wiley. Bibcode:2017AdM....2906425D. doi:10.1002/adma.201606425. ISSN 0935-9648. PMID 28417536. S2CID 205276487.
- ^ Cole, Tim; Khoshmanesh, Khashayar; Tang, Shi-Yang (2021-05-04). "Liquid Metal Enabled Biodevices". Advanced Intelligent Systems. 3 (7) 2000275. Wiley. doi:10.1002/aisy.202000275. ISSN 2640-4567. S2CID 235568215.
- ^ Tang, Shi-Yang; Tabor, Christopher; Kalantar-Zadeh, Kourosh; Dickey, Michael D. (2021-07-26). "Gallium Liquid Metal: The Devil's Elixir". Annual Review of Materials Research. 51 (1). Annual Reviews: 381–408. Bibcode:2021AnRMS..51..381T. doi:10.1146/annurev-matsci-080819-125403. ISSN 1531-7331. S2CID 236566966.
- ^ Liptak, Bela G. (2018). Instrument Engineers' Handbook, Volume Two: Process Control and Optimization. CRC Press. p. 807. ISBN 978-1-4200-6400-1.
- ^ Hickson, Paul; Borra, Ermanno F.; Cabanac, Remi; Content, Robert; Gibson, Brad K.; Walker, Gordon A. H. (1994). "UBC/Laval 2.7 meter liquid mirror telescope". The Astrophysical Journal. 436. American Astronomical Society: L201. arXiv:astro-ph/9406057. Bibcode:1994ApJ...436L.201H. doi:10.1086/187667. ISSN 0004-637X.
- ^ Hickson, Paul; Racine, Réne (2007). "Image Quality of Liquid-Mirror Telescopes". Publications of the Astronomical Society of the Pacific. 119 (854). IOP Publishing: 456–465. Bibcode:2007PASP..119..456H. doi:10.1086/517619. ISSN 0004-6280. S2CID 120735632.
- ^ a b c Krüger, Timm; Kusumaatmaja, Halim; Kuzmin, Alexandr; Shardt, Orest; Silva, Goncalo; Viggen, Erlend Magnus (2016). The lattice Boltzmann method: principles and practice. Switzerland: Springer. ISBN 978-3-319-44649-3. OCLC 963198053.
- ^ Steinhauser, M. O. (2022). Computational multiscale modeling of fluids and solids: theory and applications. Cham, Switzerland: Springer. ISBN 978-3-030-98954-5. OCLC 1337924123.
- ^ Poling, Bruce E.; Prausnitz, J. M.; O'Connell, John P. (2001). The properties of gases and liquids. New York: McGraw-Hill. ISBN 0-07-011682-2. OCLC 44712950.
- ^ Bird, R. Byron; Stewart, Warren E.; Lightfoot, Edwin N. (2007). Transport Phenomena (2nd ed.). John Wiley & Sons, Inc. ISBN 978-0-470-11539-8. Archived from the original on 2020-03-02. Retrieved 2019-09-18.
- ^ Span, R. (2000). Multiparameter Equations of State: An Accurate Source of Thermodynamic Property Data. Engineering online library. Springer. p. 1. ISBN 978-3-540-67311-8. Retrieved 2023-04-01.
- ^ Huber, Marcia L.; Lemmon, Eric W.; Bell, Ian H.; McLinden, Mark O. (2022-06-22). "The NIST REFPROP Database for Highly Accurate Properties of Industrially Important Fluids". Industrial & Engineering Chemistry Research. 61 (42). American Chemical Society (ACS): 15449–15472. doi:10.1021/acs.iecr.2c01427. ISSN 0888-5885. PMC 9619405. PMID 36329835. S2CID 249968848.
- ^ Tillner-Roth, Reiner; Friend, Daniel G. (1998). "A Helmholtz Free Energy Formulation of the Thermodynamic Properties of the Mixture {Water + Ammonia}". Journal of Physical and Chemical Reference Data. 27 (1). AIP Publishing: 63–96. doi:10.1063/1.556015. ISSN 0047-2689.
- ^ Moffatt, H.K. (2015), "Fluid Dynamics", in Nicholas J. Higham; et al. (eds.), The Princeton Companion to Applied Mathematics, Princeton University Press, pp. 467–476
- ^ Wendt, John F.; Anderson, John D. Jr.; Von Karman Institute for Fluid Dynamics (2008). Computational fluid dynamics: an introduction. Berlin: Springer. ISBN 978-3-540-85056-4. OCLC 656397653.
- ^ Pozrikidis, C. (2011). Introduction to theoretical and computational fluid dynamics. New York: Oxford University Press. ISBN 978-0-19-990912-4. OCLC 812917029.
- ^ Monaghan, J J (2005-07-05). "Smoothed particle hydrodynamics". Reports on Progress in Physics. 68 (8). IOP Publishing: 1703–1759. Bibcode:2005RPPh...68.1703M. doi:10.1088/0034-4885/68/8/r01. ISSN 0034-4885. S2CID 5987481.
- ^ Lind, Steven J.; Rogers, Benedict D.; Stansby, Peter K. (2020). "Review of smoothed particle hydrodynamics: towards converged Lagrangian flow modelling". Proceedings of the Royal Society A: Mathematical, Physical and Engineering Sciences. 476 (2241) 20190801. The Royal Society. Bibcode:2020RSPSA.47690801L. doi:10.1098/rspa.2019.0801. ISSN 1364-5021. PMC 7544338. PMID 33071565. S2CID 221538477.
- ^ Español, Pep; Warren, Patrick B. (2017-04-21). "Perspective: Dissipative particle dynamics". The Journal of Chemical Physics. 146 (15). AIP Publishing: 150901. arXiv:1612.04574. Bibcode:2017JChPh.146o0901E. doi:10.1063/1.4979514. ISSN 0021-9606. PMID 28433024. S2CID 961922.
- ^ Gompper, G.; Ihle, T.; Kroll, D. M.; Winkler, R. G. (2009). "Multi-Particle Collision Dynamics: A Particle-Based Mesoscale Simulation Approach to the Hydrodynamics of Complex Fluids". Advanced Computer Simulation Approaches for Soft Matter Sciences III. Berlin, Heidelberg: Springer Berlin Heidelberg. pp. 1–87. arXiv:0808.2157. doi:10.1007/978-3-540-87706-6_1. ISBN 978-3-540-87705-9. S2CID 8433369.
Liquid
View on GrokipediaIntroduction and Examples
Definition and Key Characteristics
A liquid is a state of matter characterized as a nearly incompressible fluid that conforms to the shape of its container while maintaining a definite volume, positioning it as an intermediate phase between the rigid solid and the highly expansive gas states.[2][8] This behavior arises from the close packing of molecules with sufficient mobility to allow flow under applied forces, distinguishing liquids from the fixed shape of solids and the lack of volume retention in gases.[9] Key characteristics of liquids include their retention of a fixed volume under constant temperature and pressure, enabling them to occupy a specific amount of space regardless of container size, coupled with their inherent ability to flow and adapt to container geometry due to weak intermolecular forces relative to thermal energy.[9] Liquids exhibit strong resistance to compression, as their molecular spacing prevents significant volume reduction under moderate pressure, and they display surface tension, which minimizes surface area and leads to cohesive behaviors at interfaces.[10] The concept of the liquid state traces back to early philosophical observations, such as those by Aristotle in the 4th century BCE, who differentiated liquids from solids within his theory of four elements—earth, water, air, and fire—attributing fluidity to the relative mobility of elemental compositions.[11] Significant advancements occurred in the 19th century with the development of kinetic theory, pioneered by Rudolf Clausius and James Clerk Maxwell, which provided a molecular foundation for understanding fluid properties through statistical mechanics, initially focused on gases but foundational for later liquid state models.[12][13] Matter fundamentally exists in several states—solids with fixed shape and volume, liquids with fixed volume but adaptable shape, gases that expand to fill containers, and plasmas as ionized gases—each defined by the balance of kinetic energy and intermolecular interactions.[2]Common Liquids and Their Importance
Among elemental liquids, mercury stands out as the only metal that remains liquid at room temperature, exhibiting a silvery appearance and high density that has historically made it useful in thermometers and barometers despite its toxicity.[14] Bromine, a reddish-brown halogen, is another notable elemental liquid at standard conditions, valued for its reactivity in chemical synthesis and water treatment applications.[15] Molecular liquids are ubiquitous in everyday life and natural processes. Water, often called the universal solvent due to its ability to dissolve a wide range of substances, covers approximately 71% of Earth's surface and is fundamental to biological systems, serving as a medium for metabolic reactions, nutrient transport, and temperature regulation in organisms.[5][16] Ethanol, a simple alcohol, plays key roles as a solvent in pharmaceuticals and cosmetics, a biofuel additive to reduce emissions, and a component in alcoholic beverages.[17] Oils, such as vegetable oils derived from plants, are essential in cooking for heat transfer and flavor enhancement, while mineral oils lubricate machinery and protect skin in personal care products.[18] The importance of these liquids extends across nature, industry, and daily life. Water's central role in life processes, from photosynthesis in plants to cellular functions in animals, underscores its indispensability for sustaining ecosystems and human health.[6] Hydrocarbons, liquid organic compounds like gasoline and diesel, power transportation and industry, providing efficient energy storage and contributing to modern economies.[19] Liquid crystals, intermediate states between liquids and solids, enable the functionality of liquid crystal displays (LCDs) in televisions, smartphones, and monitors by modulating light passage through electric fields.[20] Unique properties highlight the diversity of liquids. Liquid helium, when cooled below 2.17 K, exhibits superfluidity, flowing without viscosity and climbing container walls due to quantum effects, which aids low-temperature physics research.[21] Ionic liquids, salts that are molten at room temperature, serve as green solvents in chemical processes, offering low volatility and recyclability to minimize environmental impact compared to traditional organic solvents.[22]Macroscopic Properties
Density, Volume, and Compressibility
Liquids possess a well-defined volume under normal conditions, characterized by their density, which is defined as the mass per unit volume, .[23] This property distinguishes liquids from gases, which expand to fill their containers, and from solids, which maintain fixed shapes. For example, the density of water at 4°C and standard atmospheric pressure is approximately 1000 kg/m³, serving as a reference for many measurements.[24] Density in liquids typically decreases with increasing temperature due to thermal expansion, as the average intermolecular distances increase, leading to a larger volume for the same mass.[25] This variation is quantified through measurements at different temperatures, with most common liquids showing a consistent inverse relationship between density and temperature above their freezing points. One notable exception is water, which exhibits an anomalous density maximum at approximately 4°C under atmospheric pressure, where its density reaches about 999.97 kg/m³; below this temperature, density decreases as cooling continues toward the freezing point.[26] This behavior arises from structural changes in the hydrogen-bonded network and has significant implications for aquatic ecosystems, as it allows ice to float on water surfaces.[27] The near-constancy of liquid volume under pressure reflects their low compressibility compared to gases, where volume changes dramatically with pressure. Isothermal compressibility, defined as , quantifies this resistance to compression at constant temperature; for liquids, is typically on the order of to Pa, orders of magnitude smaller than for gases.[28] For water at room temperature, Pa.[29] This property ensures that liquids maintain structural integrity in applications like hydraulic systems. Thermal expansion in liquids is described by the volumetric thermal expansion coefficient, , which measures the fractional change in volume per unit temperature change at constant pressure.[30] Values of for typical liquids range from to K, indicating moderate expansion; for instance, ethanol has K near 20°C. In water's anomalous case, is negative between 0°C and 4°C, contributing to the density maximum.[31] The density of liquids directly underlies the principle of buoyancy, as articulated by Archimedes: the upward buoyant force on a submerged or partially submerged object equals the weight of the displaced fluid, given by , where is gravitational acceleration and is the volume of fluid displaced.[32] This force balances the object's weight for floating equilibrium when the object's density equals that of the liquid, explaining phenomena like ship flotation despite steel's higher density.[33]Viscosity, Flow, and Rheology
Viscosity quantifies the internal resistance of a liquid to shear stress, arising from intermolecular friction that opposes the relative motion of fluid layers. It is formally defined through Newton's law of viscosity, which states that the shear stress is proportional to the velocity gradient , expressed as , where is the dynamic viscosity coefficient.[34] This linear relationship holds for many common liquids under moderate shear rates, with units of viscosity in the SI system being pascal-seconds (Pa·s).[7] Liquid flow regimes are classified as laminar or turbulent based on the balance between inertial and viscous forces, predicted by the dimensionless Reynolds number , where is density, is characteristic velocity, is a length scale, and is viscosity.[35] In laminar flow, which predominates at low Reynolds numbers (typically for pipe flow), fluid particles move in smooth, parallel layers with viscous forces dominating.[36] Turbulent flow emerges at higher Reynolds numbers (often ), characterized by chaotic eddies and mixing, where inertia overwhelms viscosity and enhances momentum transfer.[36] The transition regime between these states depends on factors like pipe geometry but generally occurs around for cylindrical conduits.[35] Rheology encompasses the broader study of liquid deformation and flow under stress, distinguishing Newtonian fluids—where viscosity remains constant regardless of shear rate—from non-Newtonian fluids, whose viscosity varies with applied shear. Newtonian examples include water and most simple organic solvents, exhibiting predictable linear stress-strain behavior. Non-Newtonian liquids, common in biological and industrial contexts, include shear-thinning fluids like blood and polymer solutions, where viscosity decreases under increasing shear (e.g., blood flows more easily in narrow vessels), and shear-thickening fluids such as cornstarch suspensions, where viscosity increases with shear rate, leading to solid-like resistance under rapid stress.[37] These behaviors are modeled by power-law relations , with for shear-thinning and for shear-thickening. For steady, laminar flow of a Newtonian liquid through a straight, cylindrical tube, Poiseuille's law governs the volumetric flow rate , where is the tube radius, is the pressure difference, is viscosity, and is the tube length.[38] This equation highlights the strong dependence on radius (to the fourth power), making small changes in tube diameter profoundly affect flow, as derived from integrating the Navier-Stokes equations under no-slip boundary conditions.[39] Poiseuille's law applies strictly to incompressible, low-Reynolds-number flows and underpins applications like blood circulation modeling and microfluidic design.[38]Surface Tension and Interfaces
Surface tension is a property of liquids arising from the cohesive forces between molecules at the surface, quantified as the force per unit length, denoted by γ, that acts parallel to the surface to minimize its area. This results in phenomena such as the spherical shape of liquid droplets, where the surface contracts to achieve the lowest possible energy state.[40][41] The pressure difference across a curved liquid interface is described by the Young-Laplace equation: where ΔP is the pressure jump, and R₁ and R₂ are the principal radii of curvature. For a spherical droplet, this simplifies to ΔP = 2γ/R, explaining the higher internal pressure in small droplets compared to larger ones.[42][43] Capillary action occurs when surface tension drives a liquid up or down a narrow tube due to adhesive interactions with the tube walls, balanced against gravity. The height h of rise in a cylindrical tube is given by: where θ is the contact angle, ρ is the liquid density, g is gravitational acceleration, and r is the tube radius. Wetting liquids like water in glass (θ < 90°) rise, while non-wetting ones like mercury (θ > 90°) depress.[44][45] At liquid-liquid interfaces, such as oil and water, surface tension governs immiscibility and emulsion stability, with the interfacial tension being the difference in cohesive forces between the phases. Liquid-solid interfaces involve wetting characterized by the contact angle θ, where complete wetting (θ = 0°) spreads the liquid, and partial wetting (0° < θ < 180°) forms droplets. Gradients in surface tension, often due to temperature or concentration variations, induce the Marangoni effect, driving fluid flow from low to high tension regions, as seen in tear-like instabilities on wine surfaces.[46][47] Surface tension generally decreases with increasing temperature, as thermal energy weakens intermolecular forces; for water, it drops from about 72 mN/m at 20°C to 59 mN/m at 100°C. In soap bubbles, which have two surfaces, the excess pressure is ΔP = 4γ/R, and surfactants reduce γ to enable stable thin films, demonstrating surface tension's role in bubble formation and persistence.[48][43]Pressure Effects and Buoyancy
In liquids at rest, hydrostatic pressure increases linearly with depth due to the weight of the fluid above. The pressure at a depth below the surface is given by , where is the pressure at the surface, is the liquid density, and is the acceleration due to gravity.[49] This distribution assumes incompressible behavior and uniform density, though slight variations occur in practice.[50] Pascal's principle states that any change in pressure applied to an enclosed liquid is transmitted undiminished throughout the fluid and to the walls of its container.[51] This property enables the uniform force multiplication in hydraulic systems, where a small input force over a small area produces a larger output force over a larger area, as the pressure remains constant.[52] Buoyancy arises from the pressure difference on an immersed or floating object, resulting in an upward force equal to the weight of the displaced liquid, as described by Archimedes' principle.[53] An object floats if its average density is less than that of the liquid, sinks if greater, and remains suspended if equal, with the submerged volume adjusting to balance the weights.[32] For stability, the center of gravity of a floating object must lie below its center of buoyancy; otherwise, tilting produces a restoring torque that returns it to equilibrium, as seen in ship design where low placement of heavy cargo enhances this metacentric stability.[54][55] Under high pressure, liquids exhibit slight compressibility, leading to density increases that affect volume and pressure profiles. In deep ocean environments, water compressibility results in a density rise of about 4-5% at 10 km depth, influencing hydrostatic equilibrium and requiring corrections in pressure measurements.[56][57] In hydraulic systems, low compressibility ensures efficient pressure transmission and minimal energy loss, with fluids like mineral oils selected for bulk moduli exceeding 1.5 GPa to maintain performance under operational pressures up to hundreds of MPa.[58] Historically, Evangelista Torricelli demonstrated atmospheric pressure's role in supporting liquid columns in 1643 by inverting a mercury-filled tube into a dish, creating a vacuum above a 76 cm column balanced by air pressure, laying the foundation for barometers.[59]Thermal and Acoustic Properties
Liquids exhibit a range of thermal properties that govern their response to heat input, including specific heat capacity, thermal expansion, and thermal conductivity. The specific heat capacity at constant pressure, denoted , quantifies the amount of heat required to raise the temperature of one unit mass of the liquid by one degree Kelvin without phase change, typically measured in J/(kg·K). For water at 25°C, is approximately 4180 J/(kg·K), which is notably higher than that of many other liquids like ethanol at around 2440 J/(kg·K).[60] Thermal expansion in liquids is characterized by the volume expansion coefficient , defined such that the relative change in volume is for a temperature change , reflecting the increase in molecular kinetic energy that weakens intermolecular forces. Unlike solids, liquids generally have higher values; for example, mercury has K at room temperature. Water displays an anomalous behavior in this property, contracting upon heating between 0°C and 4°C due to enhanced hydrogen bonding, resulting in a negative in that range, which contrasts with the positive expansion above 4°C.[31][61] Heat conduction within liquids follows Fourier's law, where the heat flux is proportional to the negative temperature gradient: , with being the thermal conductivity, typically on the order of 0.1–0.6 W/(m·K) for common liquids like water ( W/(m·K) at 20°C). This property arises from molecular collisions transferring kinetic energy, though liquids conduct heat less efficiently than metals due to weaker ordered structures. Additionally, liquids possess latent heats associated with phase changes: the latent heat of fusion is the energy per unit mass to melt a solid into liquid (e.g., 334 kJ/kg for water), while the latent heat of vaporization is the energy to convert liquid to vapor (e.g., 2260 kJ/kg for water at 100°C), both reflecting the energy to overcome intermolecular forces without temperature change.[62][60]/13%3A_Heat_and_Heat_Transfer/13.3%3A_Phase_Change_and_Latent_Heat) Acoustic properties of liquids involve the propagation and damping of sound waves, with the speed of sound given by , where is the bulk modulus (a measure of resistance to compression) and is density; for water, m/s at 20°C, significantly higher than in air due to stronger intermolecular forces yielding a larger . Sound attenuation in liquids occurs primarily through viscous effects, where internal friction dissipates wave energy as heat, with the classical Stokes' relation showing attenuation coefficient , being viscosity (as discussed in prior sections on rheology). Water's high specific heat and anomalous expansion contribute to its unique acoustic profile, enabling applications like ultrasound imaging and cleaning, where high-frequency waves (above 20 kHz) exploit cavitation in liquids for processes such as emulsification and medical diagnostics./Book%3A_University_Physics_I_-Mechanics_Sound_Oscillations_and_Waves(OpenStax)/17%3A_Sound/17.03%3A_Speed_of_Sound)[63][61][64]Microscopic Structure
Molecular Ordering and Intermolecular Forces
Liquids lack the long-range translational order of crystalline solids but display short-range molecular ordering, where neighboring molecules adopt preferred spatial arrangements over distances of a few molecular diameters. This local structure is quantitatively described by the radial distribution function , which represents the probability density of finding a pair of molecules separated by distance relative to a random distribution. Peaks in indicate regions of higher density due to intermolecular attractions, with the first peak typically corresponding to the nearest-neighbor shell and subsequent oscillations reflecting packing efficiency. Such functions are routinely obtained from scattering experiments, providing direct insight into the average local environment without assuming a periodic lattice.[65][66] A prominent example of short-range ordering occurs in liquid water, where each molecule forms a locally tetrahedral coordination with four neighbors through hydrogen bonds, resulting in distinct peaks in the oxygen-oxygen at approximately 2.8 Å and 4.5 Å. This arrangement arises from the directional nature of hydrogen bonds, creating transient open structures that persist on picosecond timescales despite thermal motion. In contrast to the rigid tetrahedral lattice of ice, liquid water's coordination is dynamic, with bond breaking and reforming allowing diffusion while maintaining local order.[67][68] The short-range ordering in liquids is governed by intermolecular forces, primarily van der Waals dispersion forces (induced dipole interactions), permanent dipole-dipole attractions, and hydrogen bonding in polar molecules. These forces promote cohesion, the attraction between like molecules that holds the liquid together, while adhesion refers to attractions between liquid molecules and unlike surfaces, influencing wetting behavior. For instance, strong hydrogen bonding in water enhances cohesion, leading to high surface tension, whereas weaker van der Waals forces dominate in nonpolar liquids like hydrocarbons. These interactions balance repulsive core potentials to yield the fluid-like density of liquids.[69][70] Compared to solids, which feature extended lattices with fixed positions, and gases, where molecules are too distant for significant correlations, liquids exhibit no long-range order but form transient clusters of locally ordered molecules that continually rearrange. These clusters, often 10–100 molecules in size, emerge from cooperative attractions and contribute to the liquid's viscosity without forming a stable network. In supercooled liquids cooled below their freezing point but remaining fluid, enhanced short-range ordering leads to the glass transition, where dynamics slow dramatically and the structure freezes into an amorphous solid-like state with persistent local motifs.[71][72] X-ray and neutron diffraction serve as primary experimental methods to probe pair correlations in liquids, with neutrons particularly sensitive to light elements like hydrogen due to isotopic contrast variation. In these techniques, the scattered intensity as a function of momentum transfer is Fourier-transformed to yield , revealing coordination numbers and bond lengths with atomic resolution. For example, neutron diffraction on liquid argon shows clear oscillations in up to several coordination shells, confirming the absence of periodicity beyond short ranges.[65][68]Thermodynamic Aspects of Liquid State
The liquid state is characterized by a delicate thermodynamic balance between energetic contributions from intermolecular interactions and entropic contributions from molecular positional freedom. The potential energy in liquids arises primarily from attractive and repulsive forces between molecules, which lower the internal energy compared to the ideal gas state while allowing for diffusive motion. This energy landscape is shaped by pairwise interactions, such as van der Waals forces, that stabilize the dense packing without the long-range order of solids. A key entropic factor stabilizing the liquid phase is the configurational entropy , which quantifies the multiplicity of accessible molecular configurations due to the absence of fixed lattice positions. Unlike the translational entropy dominating dilute gases, in liquids reflects the combinatorial possibilities of rearranging molecules within a constrained volume, often estimated through statistical mechanics as , where is the number of microstates. This entropy term, arising from the disordered yet correlated molecular arrangements, compensates for the energetic cost of density, preventing collapse to a solid or expansion to a gas. Intermolecular forces, briefly, modulate the depth of the potential wells that define these configurations. The thermodynamics of liquids defies simple approximations due to the absence of a small parameter for perturbation expansions, distinguishing them from gases (where low density enables ideal gas models) and solids (where harmonic oscillators suffice). Full statistical mechanical treatments are required, as interactions are neither weak nor separable into independent modes. The free volume theory addresses this by modeling molecular motion as diffusion within unoccupied space, where the available free volume per molecule determines transport and thermodynamic properties without relying on dilute or rigid limits. This approach highlights the intermediate nature of liquids, where density is comparable to solids but dynamics resemble gases.[73][74] The molar heat capacity at constant volume for liquids approximates per atom, akin to the Dulong-Petit value for solids, as vibrational modes dominate the energy storage, with translational and rotational contributions largely saturated. Deviations from this value occur due to anharmonic effects and subtle configurational rearrangements, leading to values slightly higher or lower depending on the liquid; for example, in simple liquids like argon, is about 2.8R at the triple point, reflecting partial excitation of anharmonic modes. The enthalpy of vaporization quantifies the energetic barrier to dispersing liquid molecules into vapor, typically on the order of 5–10 at the boiling temperature , underscoring the strength of cohesive interactions.[75][75] A distinctive thermodynamic indicator of the liquid state's emergence from the solid is the Lindemann criterion for melting, which posits that a crystal melts when the root-mean-square vibrational amplitude of atoms reaches approximately 10–15% of the nearest-neighbor distance. This threshold, derived from the onset of mechanical instability in the lattice, marks the transition where thermal fluctuations overwhelm harmonic restoring forces, allowing the system to access the higher-entropy liquid configurations without a small displacement parameter.[76]Quantum Mechanical Influences
In liquids composed of light elements at low temperatures, quantum mechanical effects become prominent, altering the classical behavior expected from molecular interactions. A quintessential example is superfluid helium-4 (^4He), where Bose-Einstein condensation (BEC) underlies the transition to a superfluid state. In this process, a macroscopic number of ^4He atoms, which are composite bosons with integer spin, occupy the lowest quantum energy state, leading to coherent quantum behavior observable on macroscopic scales. This phenomenon was first proposed by Fritz London in 1938 as the mechanism for superfluidity, linking the λ-transition to the degeneracy predicted by Bose-Einstein statistics. The persistence of helium as a liquid even at absolute zero under its own vapor pressure exemplifies the role of zero-point energy, arising from the Heisenberg uncertainty principle. In ^4He, the light atomic mass and weak van der Waals forces result in a large zero-point motion that dominates the potential energy well, preventing the atoms from settling into a crystalline lattice. This quantum kinetic energy contribution is approximately seven times the depth of the interatomic potential, ensuring that solidification requires elevated pressures above 25 bar at 0 K.[77] Similarly, quantum tunneling and delocalization effects are evident in liquid para-hydrogen (p-H_2), a bosonic system where protons exhibit wave-like spreading. Path-integral simulations reveal that nuclear quantum effects lead to enhanced molecular delocalization, with wave packets showing non-classical diffusion and reduced effective viscosity compared to classical predictions.[78] In contrast, fermionic systems like liquid metals exhibit quantum influences through Fermi liquid theory, which describes the collective behavior of conduction electrons. Developed by Lev Landau in 1957, the theory posits that interacting fermions in metals such as sodium form quasiparticles that retain the properties of a non-interacting Fermi gas, albeit with renormalized parameters like effective mass. Experimental evidence includes deviations in plasma wave dispersion in liquid sodium, where the sharp Fermi surface leads to oscillatory potentials and enhanced long-range correlations beyond classical expectations.[79][80] The λ-transition in ^4He at 2.17 K marks the onset of superfluidity, characterized by a sharp peak in specific heat resembling the Greek letter λ, driven by the establishment of long-range quantum order via BEC. Below this temperature, the superfluid fraction increases, with zero viscosity and quantized vortex formation emerging as hallmarks of macroscopic quantum coherence. Path integral Monte Carlo (PIMC) simulations provide a powerful tool for probing these effects, treating particles as closed paths in imaginary time to compute properties like superfluid density through permutation exchanges, accurately reproducing the λ-point and phase diagram without approximations for bosonic liquids.[81][82]Experimental Probes of Structure
Scattering techniques provide essential insights into the microscopic structure of liquids by measuring density fluctuations and atomic correlations. X-ray scattering experiments yield the static structure factor S(q), from which the radial distribution function g(r) is derived via Fourier transform, quantifying pairwise atomic distances and local ordering in liquids like water, where peaks in g(r) correspond to first and second hydration shells at approximately 2.8 Å and 4.5 Å, respectively.[83] Neutron scattering complements this by exploiting isotopic contrasts to isolate contributions from specific atomic pairs, enabling precise mapping of intermolecular forces in complex liquids such as molten salts or alloys.[84] These methods reveal short-range order akin to that in solids but with diffusive broadening due to thermal motion. Inelastic variants of scattering extend probes to dynamics. Inelastic neutron scattering measures the dynamic structure factor S(q,ω), capturing phonon-like collective excitations and diffusion processes, with intermediate scattering functions indicating relaxation times on the order of picoseconds in simple liquids.[85] Similarly, inelastic X-ray scattering resolves momentum- and energy-dependent correlations, allowing real-space visualization of molecular motions via the Van Hove function, as demonstrated in studies of hydrogen bond breaking in liquid water.[86] Spectroscopic methods offer complementary views of liquid microstructure through molecular-level interactions. Nuclear magnetic resonance (NMR) diffusometry, using pulsed field gradients, quantifies self-diffusion coefficients D, linking them to local viscosity and cage effects; in neat liquids, D values around 10^{-9} m²/s reflect barrier crossing in dense environments.[87] Raman and infrared (IR) spectroscopies detect vibrational spectra, where band positions and widths indicate bond strengths and anharmonicities; in liquid water, the asymmetric OH stretch at ~3400 cm⁻¹ broadens due to hydrogen bond diversity, distinguishing tetrahedral from disrupted structures.[88] Ultrafast spectroscopy captures transient structural changes. Femtosecond time-resolved X-ray absorption spectroscopy, often at water-window energies, tracks core-level shifts following optical excitation, revealing solvation dynamics and charge redistribution in liquids on sub-picosecond scales.[89] For instance, in urea solutions, this technique observes femtosecond proton transfer, with spectral changes evidencing altered hydrogen bonding networks.[90] Additional probes focus on relaxation timescales tied to structure. Dielectric relaxation spectroscopy measures frequency-dependent permittivity to extract Debye relaxation times τ, probing dipole reorientation; in water, a primary τ ≈ 8.3 ps reflects cooperative H-bond dynamics, with faster sub-picosecond components from local librations.[91] Viscosity measurements, via rotational or capillary methods, indirectly inform structural timescales through Stokes-Einstein relations, where η ~ 1/D highlights caging effects in viscous liquids like glycerol.[92] Recent advancements leverage synchrotron and free-electron laser sources for real-time structural interrogation. High-brilliance synchrotron X-ray scattering enables sub-millisecond resolution of evolving microstructures, such as nanocrystal ordering in evaporating colloidal liquids.[93] Ultrafast techniques, integrating femtosecond pulses with scattering, overcome traditional limits, providing snapshots of non-equilibrium states in photoexcited liquids and advancing understanding of femtosecond-scale transients.[86]Phase Transitions
Solid-Liquid Transitions
The solid-liquid transition, also known as melting or freezing, represents the phase change between a crystalline solid and its liquid counterpart at equilibrium conditions. This process occurs reversibly at the melting point, where the solid and liquid phases coexist with equal chemical potentials, determined by the condition that the change in Gibbs free energy, ΔG, is zero for the transformation solid ↔ liquid.[94] At this temperature, the entropy increase upon melting balances the enthalpy of fusion, satisfying ΔG = ΔH_fus - T ΔS = 0.[95] The thermodynamics of the solid-liquid boundary are described by the Clapeyron equation, which relates the slope of the phase boundary in a pressure-temperature diagram to the changes in enthalpy and volume: dP/dT = ΔH / (T ΔV). Here, ΔH is the enthalpy of fusion (positive for melting), T is the absolute temperature, and ΔV is the volume change upon melting, typically positive for most substances since liquids are less dense than their solids, leading to an increase in melting point with pressure.[95] For water, however, ΔV is negative because ice Ih is less dense than liquid water, resulting in a negative slope and a decrease in melting point with increasing pressure, which facilitates the formation of high-pressure ice polymorphs like ice II and ice VI under extreme conditions.[96] The latent heat of fusion, ΔH_fus, quantifies the energy required to melt a unit mass of solid at the melting point, representing the heat absorbed during the phase change without a temperature rise. This energy overcomes the intermolecular forces in the solid lattice, transitioning the material to the more disordered liquid state.[97] Freezing, the reverse process, releases this latent heat. The kinetics of these transitions are influenced by nucleation barriers; supercooling occurs when a liquid is cooled below its melting point without solidifying due to the high free energy barrier for forming a critical nucleus of the solid phase, which requires overcoming surface energy costs.[98] Overcooling can reach several degrees Kelvin in pure liquids before homogeneous nucleation initiates crystallization.[97] Impurities significantly affect the solid-liquid transition by depressing the melting point and broadening the temperature range over which melting occurs. In binary alloys, eutectic compositions exhibit the lowest melting point, where a liquid phase coexists with two solid phases at a specific temperature, enabling applications in materials processing. Pressure dependence varies with material; for instance, the multiple polymorphs of ice under high pressure each have distinct melting curves, with transitions like ice Ih to ice III occurring around 200 MPa and -22°C.[95] A notable feature of water's phase behavior is its triple point, where solid, liquid, and vapor phases coexist in equilibrium at 0.01°C and 611 Pa.[99] This point marks the end of the solid-liquid boundary at low pressures.Liquid-Vapor Transitions
Liquid-vapor transitions encompass the processes of boiling, where a liquid converts to vapor upon reaching its boiling point, and condensation, the reverse process where vapor forms liquid droplets. These transitions occur at the interface between the liquid and vapor phases and are governed by the vapor pressure of the liquid, which increases with temperature. The relationship between vapor pressure and temperature is described by the Clausius-Clapeyron equation, derived from thermodynamic considerations of phase equilibrium: where is the enthalpy of vaporization, is the gas constant, and is a constant specific to the substance. This equation applies to the coexistence curve in the phase diagram and predicts how vapor pressure changes during the transition. The normal boiling point is defined as the temperature at which the vapor pressure equals 1 atm (standard atmospheric pressure), marking the condition for boiling at sea level.[100][101] In vapor-liquid equilibrium (VLE), the liquid and vapor phases coexist when the partial pressure of the vapor equals the vapor pressure of the liquid at that temperature. For pure substances, boiling initiates when the applied pressure drops to or below the vapor pressure, but practical boiling often requires nucleation sites to form vapor bubbles. Nucleation can be heterogeneous, occurring at impurities or surface imperfections that lower the energy barrier for bubble formation, or homogeneous, in the bulk liquid under superheated conditions. Cavitation refers to the formation of vapor cavities or bubbles in a liquid due to localized pressure reductions below the vapor pressure, often in flowing systems, leading to rapid bubble growth and potential collapse. For ideal binary mixtures, Raoult's law approximates VLE by stating that the partial vapor pressure of a component is its mole fraction in the liquid times its pure-component vapor pressure: . This law holds for systems with similar intermolecular forces but deviates in non-ideal cases.[102][103][104] The critical point represents the end of the liquid-vapor coexistence curve, where the distinction between liquid and vapor phases disappears. At this point, the difference in molar volumes between the phases , and properties like density become identical for both phases, eliminating the meniscus and causing surface tension to vanish. Above the critical temperature and critical pressure , the substance exists as a supercritical fluid, exhibiting hybrid properties of liquids and gases, such as low viscosity and high diffusivity. For example, supercritical carbon dioxide (C, bar) is widely used as a green solvent in extractions due to its tunable density and non-toxicity. These phenomena highlight the continuous nature of the fluid state beyond traditional phase boundaries.[105][106] Triple points and critical points provide key coordinates for understanding phase behavior in common liquids. The triple point is where solid, liquid, and vapor phases coexist in equilibrium. For water, the triple point is at C and 611.2 Pa, while its critical point is at C and 217.75 atm. Carbon dioxide has a triple point at C and 5.17 bar, with a critical point at C and 73.8 bar. Ethanol's critical point occurs at C and 63.8 bar, and its triple point at approximately C and low pressure (around bar).[107][108][109] These values illustrate the range of conditions under which liquid-vapor transitions manifest across substances.| Substance | Triple Point Temperature (°C) | Triple Point Pressure (bar) | Critical Temperature (°C) | Critical Pressure (bar) |
|---|---|---|---|---|
| Water | 0.01 | 0.006112 | 374 | 220.6 |
| CO₂ | -56.6 | 5.17 | 31.1 | 73.8 |
| Ethanol | -114 | 7.4 \times 10^{-9} | 241 | 63.8 |
Multicomponent and Exotic Transitions
In multicomponent liquid systems, phase transitions exhibit complex behaviors due to interactions between constituents, often visualized through boiling point diagrams that map temperature-composition relationships during vapor-liquid equilibrium. These diagrams reveal regions where mixtures deviate from ideal behavior, such as positive or negative deviations from Raoult's law, leading to maximum or minimum boiling points.[110] Azeotropes form at these extrema, where the vapor and liquid phases have identical compositions, rendering simple distillation ineffective for separation; for instance, the ethanol-water system forms a minimum-boiling azeotrope at 95.6% ethanol by weight, boiling at 78.2°C.[111] Boiling point diagrams for binary mixtures typically show lens-shaped two-phase regions, with tie lines connecting coexisting liquid and vapor compositions, and the azeotrope appearing as a point where the liquidus and vaporus curves intersect.[112] Peritectic reactions in multicomponent systems involving liquids occur as invariant transformations where a liquid phase reacts with a solid phase to form a new solid phase at a specific temperature, often observed in metallic alloys during cooling. In the Cu-Sn system, for example, a peritectic reaction at 415°C involves liquid (21 wt.% Cu) and primary δ-phase solid reacting to form β-phase tin bronze, though the reaction is typically incomplete due to diffusion limitations, resulting in microstructures with residual primary phases.[113] These reactions are depicted in phase diagrams as horizontal lines at the peritectic temperature, connecting the liquid composition outside the solid tie line to the product solid, highlighting the role of liquid in facilitating solid-state transformations in mixtures.[114] Exotic liquid transitions include mesophases in liquid crystals, where molecules exhibit partial orientational and positional order intermediate between isotropic liquids and crystals. The nematic phase features long-range orientational order of rod-like molecules along a director axis but no positional order, allowing fluid-like flow while maintaining anisotropy; transitions to this phase occur via weak first-order processes from the isotropic liquid.[115] Smectic phases introduce layered structures with positional order in one dimension, as in the smectic-A variant where molecules align perpendicular to layers, exhibiting higher viscosity and transitions often involving higher-order discontinuities; for example, 4-n-octyloxy-4'-cyanobiphenyl (8OCB) displays a smectic-A phase between its nematic and crystal states.[116] The glass-liquid transition in amorphous materials represents a non-equilibrium kinetic process where supercooled liquids increase in viscosity by orders of magnitude (typically to ~10^12 Pa·s) without a thermodynamic phase change, marking the shift from a brittle glass to a viscous liquid upon heating.[117] Supercritical fluids, accessed beyond the critical point of pure substances (e.g., 374°C and 218 atm for water), lack distinct liquid-vapor phases, instead forming a continuous state with hybrid properties tunable by density; no phase boundary exists, though Widom lines may indicate crossovers in thermodynamic response.[118] Ionic liquids often show no sharp melting but exhibit glass transitions or percolation thresholds to ionic liquid crystal phases, where nanoscale segregation of charged and apolar domains leads to ordered mesophases upon cooling; a seminal study on protic ionic liquids demonstrated this percolation via molecular dynamics, with side-chain length dictating the transition.[119] Recent developments in deep eutectic solvents (DES), formed by hydrogen-bond donors and acceptors like choline chloride-urea, reveal eutectic points lowering melting temperatures dramatically (e.g., to 12°C for the 1:2 mixture), with phase diagrams estimated via machine learning from structural data to predict binary behaviors without distinct supercritical phases.[120]Liquid Mixtures and Solutions
Formation and Types of Solutions
The formation of solutions in liquids begins with the process of solvation, where solvent molecules surround and interact with solute particles, creating structured layers known as solvation shells. These shells form due to attractive intermolecular forces between the solute and solvent, stabilizing the dissolved state and facilitating the dispersion of the solute throughout the solvent.[121] In aqueous solutions, for instance, polar water molecules orient their dipole moments toward charged or polar solutes, forming the first solvation shell, while subsequent layers exhibit more disordered arrangements.[122] The thermodynamic driving force for solution formation involves changes in both enthalpy (ΔH_mix) and entropy (ΔS_mix). The enthalpy of mixing, ΔH_mix, accounts for the energy changes from breaking solute-solute, solvent-solvent, and forming solute-solvent interactions; exothermic mixing (negative ΔH_mix) favors dissolution when solute-solvent attractions outweigh the separated components' interactions.[123] Meanwhile, the entropy of mixing, ΔS_mix, generally increases due to the greater disorder from dispersing solute molecules into the larger solvent volume, often providing the primary entropic contribution to spontaneity even if ΔH_mix is slightly positive.[124] For ideal solutions, ΔS_mix follows the relation ΔS_mix = -nR (x_1 \ln x_1 + x_2 \ln x_2), where n is the total moles, R is the gas constant, and x_i are mole fractions, reflecting combinatorial mixing probabilities.[123] Solutions are classified by the extent of mixing between solute and solvent. Miscible liquids, such as ethanol and water, mix in all proportions to form a homogeneous single phase, driven by compatible intermolecular forces like hydrogen bonding.[125] In contrast, immiscible liquids, like oil and water, do not mix appreciably and separate into distinct layers due to unfavorable interactions, such as the hydrophobic effect in nonpolar hydrocarbons with polar solvents.[125] Solutions are further categorized by concentration: dilute solutions have low solute amounts where solute-solute interactions are negligible, approximating ideal behavior, whereas concentrated solutions involve significant solute-solute interactions, leading to deviations from ideality.[124] Solubility in liquid solutions follows the empirical principle "like dissolves like," which states that solutes dissolve best in solvents with similar polarity and intermolecular forces, minimizing the free energy of mixing.[126] For example, nonpolar solutes like benzene dissolve readily in nonpolar solvents like hexane through van der Waals forces, while polar or ionic solutes favor polar solvents like water via dipole-dipole or ion-dipole interactions.[127] This rule arises from the dominance of solute-solvent over solute-solute or solvent-solvent attractions, quantifiable through cohesive energy densities in regular solution theory.[127] The solubility of solutes in liquids often depends on temperature, with gases exhibiting decreased solubility as temperature rises. This inverse relationship stems from the exothermic nature of gas dissolution, where higher temperatures shift equilibrium toward the gaseous state per Le Chatelier's principle, reducing the exothermic ΔH_mix contribution.[128] For instance, oxygen solubility in water drops from about 8 mg/L at 25°C to 5 mg/L at 50°C under atmospheric pressure.[129] A key relation for gas solubility is Henry's law, which states that the mole fraction of gas in the liquid (x) is proportional to its partial pressure (P) above the solution: x = k_H P, where k_H is the Henry's law constant specific to the gas-solvent pair at a given temperature.[130] This law, formulated in 1803 by English chemist William Henry through systematic measurements of gas absorption in water, applies to dilute solutions and low pressures, providing a foundational description of gas-liquid equilibria.[131]Solubility and Phase Behavior
Solubility curves for liquid mixtures illustrate the equilibrium limits of mutual solubility as a function of temperature and composition, delineating regions of complete miscibility from partial immiscibility. In many binary systems, solubility exhibits a strong temperature dependence; for instance, in mixtures with an upper critical solution temperature (UCST), the mutual solubility increases with rising temperature until a single phase forms above the consolute point. The phenol-water system exemplifies this behavior, where the two liquids are partially miscible below the UCST of approximately 66.6 °C, beyond which they become fully miscible across all compositions.[132] The addition of electrolytes can alter these curves through effects analogous to the common ion effect, where ions common to the mixture reduce solubility by enhancing phase separation, as observed when salts like sodium chloride raise the UCST in phenol-water mixtures by up to several degrees depending on concentration.[133] Phase diagrams for binary liquid-liquid systems map these solubility behaviors, often featuring binodal curves that separate single-phase and two-phase regions, with consolute points marking the limits of miscibility. Systems exhibiting a UCST, such as hexane-nitrobenzene (UCST ≈ 19 °C), show a lens-shaped two-phase region below the consolute temperature, where compositions within the lens separate into two liquid phases of differing compositions.[134] Conversely, systems with a lower critical solution temperature (LCST), like triethylamine-water (LCST ≈ 18.3 °C), display phase separation above the consolute point due to entropy-driven immiscibility at higher temperatures.[135] In the two-phase region of such diagrams, the lever rule quantifies phase compositions and relative amounts: for an overall composition , the fraction of phase (with composition ) is , and similarly for phase , enabling prediction of phase distributions at equilibrium. Immiscibility in liquid mixtures leads to macroscopic phase separation, but stabilized dispersions can form under certain conditions. Emulsions arise from mechanically dispersing one immiscible liquid into another, creating kinetically stable droplets (typically 0.1–100 μm) stabilized by emulsifiers that reduce interfacial tension and prevent coalescence.[136] Microemulsions, by contrast, are thermodynamically stable, isotropic systems of nanoscale domains (10–100 nm) formed spontaneously in ternary or quaternary mixtures of oil, water, surfactant, and often a cosurfactant, appearing as clear, low-viscosity fluids due to ultralow interfacial tensions (10^{-3}–10^{-4} mN/m).[137] The Gibbs phase rule, , dictates the variability in these systems; for a binary liquid in a two-phase equilibrium at fixed pressure, , resulting in univariant curves (e.g., solubility boundaries) in temperature-composition space, while microemulsions often behave as single phases (, for ternary systems).[138] In modern polymer solutions, phase behavior frequently combines UCST and LCST features, yielding closed-loop miscibility gaps in temperature-composition diagrams, as seen in systems like poly(N-isopropylacrylamide)-water, where LCST dominates around 32 °C for thermoresponsive applications. These behaviors arise from competing enthalpic and entropic contributions to mixing, enabling tunable phase separation in polymer blends and solutions beyond simple small-molecule systems.[139]Colligative and Non-Ideal Properties
Colligative properties of liquid solutions are those that depend solely on the number of solute particles present, rather than their chemical identity, and arise from the dilution effect of the solute on the solvent. These properties include vapor pressure lowering, boiling point elevation, freezing point depression, and osmotic pressure, all of which stem from the reduced availability of solvent molecules at the surface or interfaces due to solute particles. In ideal dilute solutions, these effects are proportional to the mole fraction or molality of the solute.[140][141] Vapor pressure lowering occurs when a nonvolatile solute is added to a solvent, reducing the partial pressure of the solvent in the solution according to Raoult's law, expressed as , where is the mole fraction of the solute and is the vapor pressure of the pure solvent. This leads to boiling point elevation, where the temperature increase (with as the ebullioscopic constant and as molality) requires higher energy to achieve the same vapor pressure. Similarly, freezing point depression follows (with as the cryoscopic constant), as the solute stabilizes the liquid phase over the solid. Osmotic pressure, the pressure needed to prevent solvent flow across a semipermeable membrane, is given by , where is the van't Hoff factor accounting for particle dissociation, is the molar concentration, is the gas constant, and is temperature.[142][143][144] Non-ideal solutions deviate from these ideal behaviors due to intermolecular interactions between solute and solvent molecules, quantified by activity coefficients that modify concentrations in thermodynamic expressions, such that the effective concentration is for mole fraction . The van't Hoff factor adjusts for dissociation in electrolytes (e.g., for NaCl assuming complete ionization), but in non-ideal cases, it varies with concentration due to ion pairing or incomplete dissociation. Raoult's law applies to the solvent in concentrated solutions ( near ), while Henry's law governs dilute solutes (, with as Henry's constant), bridging ideal and real behaviors in mixtures./24:Solutions_I-_Volatile_Solutes/24.07:_Activities_of_Nonideal_Solutions)/17:_Solutions/17.06:_Raoults_Law_and_Henrys_Law) For electrolyte solutions, non-ideality is pronounced due to long-range electrostatic interactions, addressed by the Debye-Hückel theory, which models ions as point charges surrounded by an ionic atmosphere that screens their charge, leading to a mean ionic activity coefficient , where is a temperature-dependent constant, are ion charges, and is ionic strength. This limiting law applies to dilute solutions (typically M) and explains deviations in colligative properties like osmotic pressure for salts. The theory, developed in 1923, predicts activity coefficients approaching unity at infinite dilution and increasing deviations with concentration or charge./16:_The_Chemical_Activity_of_the_Components_of_a_Solution/16.18:Activities_of_Electrolytes-_The_Debye-Huckel_Theory) Osmosis, a key colligative phenomenon, drives water movement across biological membranes in processes like cell turgor maintenance, where semipermeable lipid bilayers selectively allow solvent passage to equalize concentrations. In technology, reverse osmosis applies external pressure exceeding osmotic pressure to desalinate seawater, producing potable water by forcing pure solvent through membranes while retaining salts, as implemented in large-scale plants worldwide.[145][146]Practical Applications
Engineering and Industrial Uses
In mechanical engineering, liquids play a pivotal role in hydraulic systems, where Pascal's principle enables the transmission of force through enclosed fluids. This principle states that a pressure change applied to an incompressible fluid in a confined system is transmitted undiminished throughout the fluid and to the walls of the container.[147] In hydraulic brakes, for instance, the force applied to the brake pedal generates pressure in the brake fluid, which is amplified to actuate the brake pads at each wheel, providing efficient stopping power in vehicles.[51] Similarly, hydraulic transmissions in heavy machinery, such as excavators and presses, leverage this principle to multiply input force for lifting or pressing operations. The incompressibility of liquids like hydraulic oil ensures precise force transmission with minimal energy loss, allowing for compact designs that handle high loads effectively.[148][149] Lubrication represents another critical engineering application of liquids, reducing friction and wear in mechanical components through distinct regimes. In boundary lubrication, which occurs under high loads and low speeds, the lubricant film is thin, resulting in direct asperity-to-asperity contact between surfaces, where additives form protective layers to minimize metal-to-metal interaction.[150] Conversely, hydrodynamic lubrication prevails at higher speeds and lower loads, where the liquid lubricant forms a full, pressurized film that completely separates the surfaces, preventing contact and enabling smooth operation in bearings and gears. The effectiveness of lubricating oils in transitioning between these regimes is often characterized by the viscosity index (VI), a measure of how viscosity changes with temperature; oils with a high VI (typically above 95 for synthetics) maintain stable performance across varying thermal conditions, crucial for engines and industrial machinery.[151][152] In chemical engineering, liquids are central to distillation processes for separating multicomponent mixtures based on differences in volatility. Fractional distillation exploits the varying boiling points of components, where more volatile substances vaporize preferentially and are condensed in stages, allowing purification of liquids like petroleum fractions or alcohols in industrial refineries.[153] The McCabe-Thiele method provides a graphical approach to design such columns for binary mixtures, plotting equilibrium curves and operating lines to determine the minimum number of theoretical stages required for separation under constant molar overflow assumptions.[154] This technique simplifies column sizing by integrating reflux ratios and feed conditions, widely applied in petrochemical and pharmaceutical production. Liquid metals extend industrial applications to high-temperature environments, particularly in energy systems. Sodium, with its low melting point and excellent thermal conductivity, serves as a coolant in sodium-cooled fast reactors, facilitating efficient heat transfer from the core to secondary systems while operating at low pressure to enhance safety and neutron economy.[155] Historically, mercury was used in thermometers due to its high density and uniform thermal expansion, enabling precise temperature measurements from the early 18th century until health concerns led to its phase-out in favor of safer alternatives.[156][157]Biological and Chemical Roles
In biological systems, water serves as the primary solvent, facilitating the dissolution of ions, metabolites, and macromolecules essential for cellular processes such as protein folding, enzyme catalysis, and nutrient transport.[158] Its high dielectric constant and hydrogen-bonding capacity enable the stabilization of charged species and the mediation of biochemical reactions within the crowded intracellular environment.[159] Blood plasma, the liquid component of blood, exhibits borderline non-Newtonian rheology due to its protein content, particularly fibrinogen and albumin, which influence viscosity under varying shear rates and contribute to hemodynamic stability.[160] This viscoelastic behavior allows plasma to adapt to circulatory demands, preventing excessive flow resistance in microvasculature while maintaining suspension of cellular elements.[161] Lipid bilayers in cell membranes demonstrate liquid-like fluidity, arising from the amphiphilic nature of phospholipids that form a dynamic, two-dimensional fluid phase at physiological temperatures.[162] This fluidity, modulated by cholesterol and unsaturated fatty acids, enables membrane deformation, protein mobility, and selective permeability, crucial for cellular signaling and division.[163] Protoplasm, the living content of cells, behaves as a non-Newtonian fluid, exhibiting thixotropy and elasticity due to its colloidal structure of proteins and organelles, which allows reversible structural changes in response to mechanical stress.[164] In prebiotic chemistry, liquid droplets formed by evaporating solutions of organic molecules, such as peptides and nucleotides, concentrate reactants and drive non-associative phase separation, potentially enabling early polymerization and protocell formation on ancient Earth.[165] An emerging phenomenon in cellular biology is liquid-liquid phase separation (LLPS), where biomolecules like proteins and RNA form membraneless condensates that organize biochemical reactions without lipid boundaries.[166] These biomolecular condensates, enriched in intrinsically disordered proteins, act as hubs for processes like transcription and stress response, with their liquid properties allowing dynamic material exchange.[167] In chemical contexts, liquids function as reaction media by solvating reactants, stabilizing transition states, and influencing selectivity through intermolecular interactions.[168] Water, in particular, plays a key role in acid-base catalysis by solvating protons and bases, facilitating proton transfer and enhancing reaction rates in aqueous environments via hydrogen-bond networks.[169] Ionic liquids, as tunable, non-volatile solvents, promote green chemistry by enabling catalyst recycling and reducing volatile organic compound use in processes like hydrogenation and extraction.[170]Everyday and Technological Implementations
In everyday cooking, boiling involves immersing food in water heated to its boiling point, typically around 100°C at sea level, where rapid vaporization facilitates heat transfer and cooks items like vegetables or pasta efficiently.[171] This process not only denatures proteins and breaks down starches but also enhances flavor extraction in stocks and broths. Emulsions, such as those in mayonnaise, form stable mixtures of oil droplets dispersed in water using emulsifiers like lecithin from egg yolks, preventing separation and creating a creamy texture essential for dressings and sauces.[172] Beverages, primarily water-based liquids, play a crucial role in human hydration by maintaining bodily functions, transporting nutrients, and regulating temperature, with daily intake recommendations around 2-3 liters for adults to prevent dehydration.[173][174] Liquids are integral to cooling technologies, where refrigerants like R-134a, a hydrofluorocarbon, cycle through compression, condensation, expansion, and evaporation in vapor-compression systems to absorb and release heat, enabling efficient refrigeration in household appliances and air conditioners.[175] Its low toxicity and suitable thermodynamic properties make it a common replacement for older chlorofluorocarbons. In advanced electronics cooling, liquid immersion submerges components in dielectric fluids, such as engineered hydrocarbons, which have high thermal conductivity to directly absorb heat without electrical conductivity risks, enabling 5-10 times higher computing density compared to air-cooled data centers, with power usage effectiveness (PUE) reduced to below 1.1 from typical values of 1.55 and over 10% savings in IT power consumption.[176] Technological applications leverage liquid properties for precision and functionality. Liquid crystals in LCD displays consist of rod-like molecules that align under electric fields to modulate light transmission, enabling thin, energy-efficient screens in televisions, monitors, and smartphones.[177] In printing, liquid inks—formulations of pigments suspended in vehicles like water or solvents—are ejected via inkjet technology to form images on substrates, with UV-curable variants drying instantly under ultraviolet light for high-speed production.[178] Fuels like gasoline, a volatile mixture of hydrocarbons derived from petroleum, serve as liquid energy sources for internal combustion engines due to their high energy density and ability to vaporize readily for ignition.[179][180] Miscellaneous uses include cleaning agents, where liquid detergents incorporate surfactants and solvents to lower surface tension, emulsify oils, and remove dirt from surfaces through wetting and rinsing actions.[181] For fire suppression, aqueous foams generated from liquid concentrates form a blanket over flammable liquids like fuels, cooling the fire while smothering it by separating the fuel from oxygen, with fluorine-free variants increasingly adopted for environmental safety.[182][183]Modeling Liquid Properties
Macroscopic and Empirical Methods
Macroscopic and empirical methods for modeling liquid properties rely on continuum-level descriptions and data-driven correlations derived from experimental observations, avoiding detailed molecular interactions. These approaches are particularly useful for engineering predictions of thermodynamic and transport behaviors in liquids under varying conditions of temperature, pressure, and composition. The principle of corresponding states provides a foundational empirical framework for scaling liquid properties across different substances by using reduced variables normalized to critical point parameters. Specifically, the reduced temperature , where is the absolute temperature and the critical temperature, along with analogous reduced pressure and volume , allows properties like density and compressibility to be compared universally for non-polar fluids. This principle, originating from observations that fluids exhibit similar behaviors when scaled to their critical points, enables interpolation of liquid properties from limited experimental data on reference fluids. For instance, the viscosity of liquids can be correlated using the Andrade equation, , where and are empirical constants fitted to temperature-dependent measurements, capturing the exponential increase in viscosity as temperature decreases. This form has been validated for a wide range of organic liquids and metals, providing accurate predictions over moderate temperature ranges without invoking molecular theories. Thermodynamic potentials form another cornerstone, with equations of state (EOS) offering macroscopic relations between pressure, volume, and temperature for liquids. The van der Waals EOS, , where is the molar volume, accounts for intermolecular attractions, and for molecular volume exclusions, extends beyond ideal gas behavior to describe liquid compressibility and phase transitions. For liquid stability, the Gibbs free energy serves as the key potential at constant temperature and pressure, where the phase with the lowest is thermodynamically stable; minima in versus composition or volume determine coexistence curves and solubility limits in liquid mixtures. Hydrodynamic models describe the flow of liquids at macroscopic scales through the Navier-Stokes equations for incompressible flow, assuming constant density. The momentum equation is given by where is density, velocity, pressure, viscosity, and body forces; coupled with the continuity equation , it predicts laminar and turbulent behaviors in pipelines and stirred vessels. These equations underpin simulations of liquid transport in industrial processes, with empirical closures for turbulence via eddy viscosity models. For compressibility, the Tait equation empirically relates liquid volume to pressure as , where and are substance-specific empirical constants, with related to the bulk modulus at ambient pressure; it accurately fits high-pressure data for water and hydrocarbons up to gigapascal ranges.[184] Recent advancements incorporate machine learning to refine such empirical correlations, with support vector machines achieving over 97% accuracy in predicting liquid densities and viscosities from sparse datasets, surpassing traditional fits for alloy melts.Mesoscopic and Statistical Approaches
In statistical mechanics, the properties of liquids are derived from ensemble averages, with the canonical ensemble providing a foundational framework for systems in thermal contact with a heat reservoir at fixed temperature , volume , and particle number . The central quantity is the partition function , defined as where , is the thermal de Broglie wavelength, and is the potential energy of the configuration . Thermodynamic potentials, such as the Helmholtz free energy , emerge directly from , enabling predictions of bulk liquid properties like pressure and internal energy through derivatives.[185] For moderate densities, where interactions are perturbative relative to ideal gas behavior, the virial expansion expresses the equation of state as a power series in density : with virial coefficients encapsulating -body correlations; the second virial coefficient arises from pairwise interactions, while higher terms account for many-body effects, offering insights into deviations from ideality in simple liquids like argon near its triple point. This expansion converges well below the critical density but diverges in dense liquids, limiting its use to transitional regimes.[185] Mesoscopic approaches bridge atomic scales and macroscopic thermodynamics by treating liquids as continuous density fields, particularly for inhomogeneous systems such as those near interfaces or in confinement. Classical density functional theory (DFT) minimizes a free energy functional where is the ideal gas contribution, captures excess correlations (often approximated via local density or fundamental measure theory), and is an external potential; equilibrium density profiles are obtained by functional differentiation, accurately describing liquid-vapor interfaces and adsorption in porous media. Coarse-graining in soft matter further reduces complexity by mapping groups of atoms to effective beads with renormalized interactions, preserving thermodynamic consistency through iterative optimization of potentials to match target correlation functions, as applied to polymer melts and colloidal suspensions.[186][187] Fluctuations in liquid compositions are quantified via Kirkwood-Buff integrals, which relate pairwise correlations to thermodynamic derivatives in solutions: where is the radial distribution function between species and ; these integrals directly yield partial molar volumes, compressibilities, and chemical potential fluctuations, providing a rigorous link between microscopic structure and macroscopic solution non-ideality, such as in aqueous electrolytes. Integral equation theories, like the Ornstein-Zernike equation closed by approximations, further enable computation of without simulations; the Percus-Yevick approximation for hard spheres uses the closure , where is the Mayer function and the cavity distribution function, yielding an analytical equation of state (where is the packing fraction) that approximates the liquid branch up to close packing with remarkable accuracy for model systems.[188]Microscopic and Computational Simulations
Microscopic and computational simulations offer atomistic-level insights into the behavior of liquids by modeling the trajectories of individual atoms and molecules over time. These methods, primarily molecular dynamics (MD), solve Newton's equations of motion to predict properties such as diffusion coefficients, radial distribution functions, and viscosity. The pioneering work in this field was the 1964 MD simulation of liquid argon by Rahman, which used a system of 864 particles interacting via the Lennard-Jones potential to compute structural correlations, marking the first computational study of a realistic liquid system.[189] In classical MD simulations, interparticle interactions are described by empirical force fields that approximate potential energy surfaces. A common choice for simple liquids is the Lennard-Jones potential, given bywhere and parameterize the interaction strength and range, respectively, capturing repulsive and attractive van der Waals forces.[189] The Verlet algorithm integrates these equations with second-order accuracy and time-reversible properties, updating positions via
where is position, is force, is mass, and is the timestep, typically on the order of femtoseconds. Simulations proceed in phases: equilibration runs stabilize temperature and density, followed by production runs that accumulate statistics for property calculations. Specialized force fields enhance accuracy for complex liquids; for instance, the OPLS-AA model parameterizes bonded and non-bonded terms for organic molecules to reproduce liquid densities and solvation free energies, while the TIP4P water model adds a massless charge site to the TIP3P geometry for better electrostatics and hydrogen bonding in aqueous systems.[190] Various statistical ensembles, such as NVT and NPT, control thermodynamic conditions during these runs. Ab initio MD methods incorporate quantum mechanical effects for greater fidelity, particularly in systems with electronic rearrangements. The Car-Parrinello approach unifies classical MD with density functional theory (DFT) by introducing fictitious dynamics for electronic orbitals, allowing simultaneous evolution of nuclear and electronic degrees of freedom without iterative self-consistency at each step. This Lagrangian formulation,
where and are ionic and electronic kinetic energies, is the Kohn-Sham energy, and enforce orthonormality, enables simulations on picosecond timescales. Applications to liquid water have elucidated its tetrahedral structure and dynamical heterogeneity, with radial distribution functions matching neutron scattering data and revealing enhanced hydrogen bond lifetimes compared to classical models.[191] Modern computational advances, including graphics processing unit (GPU) acceleration, have dramatically improved efficiency by parallelizing force evaluations and neighbor searches, achieving speedups of 10-100 times over CPU-only implementations for systems exceeding millions of atoms. This enables longer simulations of realistic liquids, such as biomolecular solutions or ionic melts, facilitating convergence to equilibrium properties.[192]