Hubbry Logo
CoercivityCoercivityMain
Open search
Coercivity
Community hub
Coercivity
logo
8 pages, 0 posts
0 subscribers
Be the first to start a discussion here.
Be the first to start a discussion here.
Coercivity
Coercivity
Coercivity
View on Wikipedia
from Wikipedia
A family of hysteresis loops for grain-oriented electrical steel, a soft magnetic material. BR denotes retentivity and HC is the coercivity. The wider the outside loop is, the higher the coercivity. Movement on the loops is counterclockwise.

Coercivity, also called the magnetic coercivity, coercive field or coercive force, is a measure of the ability of a ferromagnetic material to withstand an external magnetic field without becoming demagnetized. Coercivity is usually measured in oersted or ampere/meter units and is denoted HC.

An analogous property in electrical engineering and materials science, electric coercivity, is the ability of a ferroelectric material to withstand an external electric field without becoming depolarized.

Ferromagnetic materials with high coercivity are called magnetically hard, and are used to make permanent magnets. Materials with low coercivity are said to be magnetically soft. The latter are used in transformer and inductor cores, recording heads, microwave devices, and magnetic shielding.

Definitions

[edit]
Graphical definition of different coercivities in flux-vs-field hysteresis curve (B-H curve), for a hypothetical hard magnetic material.
Equivalent definitions for coercivities in terms of the magnetization-vs-field (M-H) curve, for the same magnet.

Coercivity in a ferromagnetic material is the intensity of the applied magnetic field (H field) required to demagnetize that material, after the magnetization of the sample has been driven to saturation by a strong field. This demagnetizing field is applied opposite to the original saturating field. There are however different definitions of coercivity, depending on what counts as 'demagnetized', thus the bare term "coercivity" may be ambiguous:

  • The normal coercivity, HCn, is the H field required to reduce the magnetic flux (average B field inside the material) to zero.
  • The intrinsic coercivity, HCi, is the H field required to reduce the magnetization (average M field inside the material) to zero.
  • The remanence coercivity, HCr, is the H field required to reduce the remanence to zero, meaning that when the H field is finally returned to zero, then both B and M also fall to zero (the material reaches the origin in the hysteresis curve).[1]

The distinction between the normal and intrinsic coercivity is negligible in soft magnetic materials, however it can be significant in hard magnetic materials.[1] The strongest rare-earth magnets lose almost none of the magnetization at HCn.

Experimental determination

[edit]
Coercivities of some magnetic materials
Material Coercivity
(kA/m)
Supermalloy
(16Fe:79Ni:5Mo) 		0.0002[2]: 131, 133 
Permalloy (Fe:4Ni) 0.0008–0.08[3]
Iron filings (0.9995 wt) 0.004–37.4[4][5]
Electrical steel (11Fe:Si) 0.032–0.072[6]
Raw iron (1896) 0.16[7]
Nickel (0.99 wt) 0.056–23[5][8]
Ferrite magnet
(ZnxFeNi1−xO3) 		1.2–16[9]
2Fe:Co,[10] iron pole 19[5]
Cobalt (0.99 wt) 0.8–72[11]
Alnico 30–150[12]
Disk drive recording medium
(Cr:Co:Pt) 		140[13]
Neodymium magnet (NdFeB) 800–950[14][15]
12Fe:13Pt (Fe48Pt52) ≥980[16]
?(Dy,Nb,Ga(Co):2Nd:14Fe:B) 2040–2090[17][18]
Samarium-cobalt magnet
(2Sm:17Fe:3N; 10 K) 		<40–2800[19][20]
Samarium-cobalt magnet 3200[21]

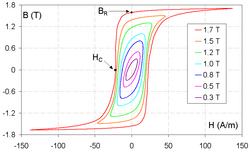
Typically the coercivity of a magnetic material is determined by measurement of the magnetic hysteresis loop, also called the magnetization curve, as illustrated in the figure above. The apparatus used to acquire the data is typically a vibrating-sample or alternating-gradient magnetometer. The applied field where the data line crosses zero is the coercivity. If an antiferromagnet is present in the sample, the coercivities measured in increasing and decreasing fields may be unequal as a result of the exchange bias effect.[citation needed]

The coercivity of a material depends on the time scale over which a magnetization curve is measured. The magnetization of a material measured at an applied reversed field which is nominally smaller than the coercivity may, over a long time scale, slowly relax to zero. Relaxation occurs when reversal of magnetization by domain wall motion is thermally activated and is dominated by magnetic viscosity.[22] The increasing value of coercivity at high frequencies is a serious obstacle to the increase of data rates in high-bandwidth magnetic recording, compounded by the fact that increased storage density typically requires a higher coercivity in the media.[citation needed]

Theory

[edit]

At the coercive field, the vector component of the magnetization of a ferromagnet measured along the applied field direction is zero. There are two primary modes of magnetization reversal: single-domain rotation and domain wall motion. When the magnetization of a material reverses by rotation, the magnetization component along the applied field is zero because the vector points in a direction orthogonal to the applied field. When the magnetization reverses by domain wall motion, the net magnetization is small in every vector direction because the moments of all the individual domains sum to zero. Magnetization curves dominated by rotation and magnetocrystalline anisotropy are found in relatively perfect magnetic materials used in fundamental research.[23] Domain wall motion is a more important reversal mechanism in real engineering materials since defects like grain boundaries and impurities serve as nucleation sites for reversed-magnetization domains. The role of domain walls in determining coercivity is complicated since defects may pin domain walls in addition to nucleating them. The dynamics of domain walls in ferromagnets is similar to that of grain boundaries and plasticity in metallurgy since both domain walls and grain boundaries are planar defects.[citation needed]

Significance

[edit]

As with any hysteretic process, the area inside the magnetization curve during one cycle represents the work that is performed on the material by the external field in reversing the magnetization, and is dissipated as heat. Common dissipative processes in magnetic materials include magnetostriction and domain wall motion. The coercivity is a measure of the degree of magnetic hysteresis and therefore characterizes the lossiness of soft magnetic materials for their common applications.

The saturation remanence and coercivity are figures of merit for hard magnets, although maximum energy product is also commonly quoted. The 1980s saw the development of rare-earth magnets with high energy products but undesirably low Curie temperatures. Since the 1990s new exchange spring hard magnets with high coercivities have been developed.[24]

See also

[edit]

References

[edit]
[edit]
Revisions and contributorsEdit on WikipediaRead on Wikipedia

Coercivity

View on Grokipedia
from Grokipedia
Coercivity, also known as the coercive field or coercive and denoted as HcH_c, is the magnitude of the reverse magnetizing required to reduce the magnetic flux density of a ferromagnetic material to zero after it has been saturated and the external field removed, effectively measuring the material's resistance to demagnetization. This property is a key parameter in the hysteresis loop of magnetic materials, appearing as the intercept on the negative horizontal axis where the magnetic flux density returns to zero. Coercivity is typically expressed in units of amperes per meter (A/m) in the SI system or oersteds (Oe) in the cgs system. In magnetic materials, coercivity distinguishes between soft and hard magnets based on its value: soft magnets exhibit low coercivity (often less than 1 kA/m), allowing easy and demagnetization with minimal loss, making them ideal for applications like cores and inductors where high permeability and low are desired. In contrast, hard magnets possess high coercivity (typically greater than 10 kA/m), enabling them to retain strong against demagnetizing fields, which is essential for permanent magnets used in motors, generators, and devices. The Magnetic Materials Producers Association defines permanent magnet materials as those with a coercive force exceeding 120 Oe (about 9.55 kA/m). Coercivity is influenced by factors such as microstructure, grain size, defects, and composition, with smaller grain sizes often enhancing it by reducing demagnetization effects in materials like rare-earth alloys. High-coercivity materials, such as neodymium-iron-boron (NdFeB) magnets, achieve values up to 1,200 kA/m, supporting advancements in compact, high-performance devices, while ongoing research focuses on optimizing these properties for energy-efficient technologies.

Fundamentals

Definition

Coercivity, denoted as HcH_c, is the strength required to reduce the density BB of a ferromagnetic material to zero after it has been saturated. This parameter quantifies the material's resistance to demagnetization and is a fundamental characteristic in the study of . Coercivity is expressed in amperes per meter (A/m) in the SI unit system or oersteds (Oe) in the cgs system, with the approximate conversion 11 Oe ≈79.58\approx 79.58 A/m. A distinction exists between normal coercivity (HcH_c or HcnH_{cn}), applicable to multidomain materials and defined as the field that reduces the average density BB to zero, and intrinsic coercivity (HciH_{ci}), relevant for single-domain particles and defined as the field that reduces the intrinsic MM to zero. Early measurements of magnetic hysteresis were conducted by James Alfred Ewing in the 1890s. Remanence, often denoted as MrM_r or BrB_r, represents the residual in a ferromagnetic after the external is removed following saturation. This property is intrinsically linked to , as both are extracted from the second quadrant of the loop: is the value at zero applied field (H=0H = 0), while coercivity is the reverse field strength required to drive the to zero. In materials with high relative to saturation, the loop exhibits greater "squareness," indicating efficient retention of magnetic state, which complements high coercivity in permanent magnet applications. Saturation , MsM_s, denotes the maximum achievable when all magnetic moments in the are fully aligned by a sufficiently strong applied field. Unlike , which measures the resistance to demagnetization from this saturated state, MsM_s sets the upper limit on the material's magnetic strength and is a fundamental intrinsic property influenced by composition and . The contrast is evident in the loop, where defines the field needed to nullify starting from MsM_s, highlighting how high- materials maintain alignment against opposing fields while approaching their saturation limit. Magnetic susceptibility χ\chi and permeability μ\mu quantify a material's response to applied fields, with μ=μ0(1+χ)\mu = \mu_0 (1 + \chi) relating induction to . Low-coercivity (soft) magnetic materials feature high χ\chi and μ\mu (often μr>1000\mu_r > 1000), enabling rapid and efficient for applications like transformers, whereas high-coercivity (hard) materials exhibit low χ\chi and μ\mu (typically μr≈1.05\mu_r \approx 1.05), prioritizing stability over ease of . This distinction arises because elevated coercivity suppresses reversible motion and moment rotation, reducing overall susceptibility. Beyond standard coercivity HcH_c, remanent coercivity HcrH_{cr} specifically denotes the reverse field applied to reduce the remanence MrM_r to zero after initial saturation and field removal. It is determined from the demagnetization curve as the field strength at which the magnetization reaches zero when starting from the remanent state (H=0, M=M_r). This parameter is particularly relevant for evaluating demagnetization resistance in permanent magnets, often exceeding HcH_c in hard materials due to irreversible processes. Illustrative examples underscore these relations: soft magnets like commercial iron exhibit low coercivity (Hc<1H_c < 1 kA/m, typically 0.2–0.7 kA/m) and high permeability, ideal for electromagnetic cores in transformers where minimal energy loss during cycling is essential. In contrast, hard magnets such as NdFeB alloys display high coercivity (Hc>800H_c > 800 kA/m, e.g., up to 1115 kA/m in high-grade variants) and substantial , enabling their use in compact permanent magnets for motors and generators.

Measurement

Experimental Techniques

The primary experimental technique for determining coercivity involves generating a hysteresis loop using a (VSM), which measures the MM as a function of applied HH. In this method, the sample is first saturated by applying a sufficiently strong magnetic field in one direction to align all magnetic moments, typically exceeding the saturation field HsH_s. The field is then gradually reduced to zero, resulting in remanent magnetization MrM_r, followed by the application of a reverse field until the magnetization crosses zero, at which point the applied field value corresponds to the coercivity HcH_c. This process traces the full loop, from which HcH_c is extracted as the reverse field magnitude where M=0M = 0 in the second quadrant. VSM operates by vibrating the sample in a uniform magnetic field, inducing a voltage in pickup coils proportional to the sample's via , enabling precise measurements over a wide range of fields up to 7 T and temperatures from cryogenic to elevated levels. Alternative techniques include magnetometry, particularly suited for low-field measurements and small samples where high sensitivity (down to 10−810^{-8} emu) is required, such as in with coercivities below 1 kA/m. SQUIDs detect minute magnetic fluxes using superconducting loops, allowing loops to be traced similarly to VSM but with superior resolution for weak signals at fields as low as 0.001 T. For industrial applications, hysteresisgraphs provide rapid, automated testing of bulk permanent magnets, applying pulsed or cyclic fields to generate loops and determine HcH_c in seconds, often up to 2.5 T, without the need for sample . These instruments are optimized for , handling larger samples like magnet blocks. Coercivity exhibits time and frequency dependence due to magnetic , a thermally activated where domain walls or moments relax slowly, leading to higher HcH_c values at faster rates. In DC measurements, which use quasi-static field sweeps (e.g., 1-10 Oe/s), HcH_c reflects equilibrium conditions, whereas AC measurements at frequencies of 1-1000 Hz or rapid sweeps introduce dynamic effects, increasing HcH_c by 10-50% in soft materials like ferrites, as the system cannot fully relax. For instance, in NdFeB magnets, HcH_c rises with sweep rate RR according to dHcdln⁡R≈S\frac{dH_c}{d \ln R} \approx S, where SS is the . Sample preparation is crucial for accurate HcH_c determination, beginning with demagnetization to eliminate prior , typically via alternating field (AF) cycling in a tumbler or thermal treatment above the , followed by cooling in zero field. Samples are then mounted on a non-magnetic holder (e.g., quartz rod) aligned with the field axis, ensuring minimal shape anisotropy. Field calibration involves verifying the or superconducting coil using a reference standard like a proton NMR or Hall sensor, achieving accuracy better than 0.1%. Powders may require epoxy encapsulation to prevent reorientation during vibration.
MaterialTypical Coercivity (HcH_c)Notes/Source
(Ni-Fe)~11 A/mSoft magnetic ; bulk value for high-permeability grades.
(cast)50-150 kA/mPermanent magnet; varies by grade (e.g., Alnico 5).
SmCo (1:5 type)500-2000 kA/mHigh-temperature permanent magnet; annealed ribbons.
FePt nanoparticles~5 MA/mL1₀-ordered, ~5-10 nm size; typical for chemically synthesized nanoparticles.
Error sources in HcH_c measurements include demagnetization effects from sample , which distort the internal field. The corrected internal field is given by Hcorrected=Hmeasured+N⋅MH_{\text{corrected}} = H_{\text{measured}} + N \cdot M, where NN is the demagnetization factor (0 for needles along the field, 1/3 for spheres) and MM is the ; this adjustment is applied point-by-point to the hysteresis loop for non-ellipsoidal samples to obtain intrinsic properties. Other errors arise from field inhomogeneity (mitigated by sample positioning) or thermal drifts, typically contributing <1% uncertainty in calibrated VSM setups.

Hysteresis Loop Analysis

The hysteresis loop in ferromagnetic materials graphically represents the relationship between the applied magnetic field strength HH and the magnetization MM, illustrating the material's nonlinear and history-dependent response during magnetization reversal. The major hysteresis loop is obtained by cycling the field from positive saturation, where MM reaches its maximum value MsM_s, through zero field to negative saturation, enclosing an area that quantifies energy dissipation. Key points on the loop include saturation magnetization MsM_s at high fields, remanent magnetization MrM_r (briefly referenced as the residual MM at H=0H=0), and coercivity HcH_c, marking the reverse field needed to reduce MM to zero. Minor loops, formed by incomplete field cycles, reveal dynamic effects such as loop widening under time-varying fields, providing insights into reversible and irreversible processes without reaching saturation. Coercivity HcH_c is extracted from the major loop as the value of HH where the demagnetization curve intersects the M=0M=0 axis, directly measuring the field's resistance to domain reversal. This intrinsic coercivity HciH_{ci} applies specifically to the MM-HH curve and differs from the normal coercivity HcH_c on the BB-HH loop, where demagnetizing fields influence the intersection; high-field extrapolations distinguish HciH_{ci} by extending the linear portion of the second quadrant to M=0M=0, avoiding artifacts from sample shape. For accurate determination, loops are measured under quasi-static conditions to minimize dynamic broadening. The area of the hysteresis loop correlates with coercivity through its representation of energy dissipation per cycle, as higher HcH_c typically widens the loop, increasing the enclosed area and thus hysteresis loss. The energy loss WW per unit volume for a closed loop in the MM-HH plane is given by the line integral W=∮H dMW = \oint H \, dM, which quantifies the work done by the field against irreversible domain wall motion and pinning. To derive this, consider the magnetic energy density supplied by the external field during a small field change dHdH: the incremental work is H dB=μ0H(dM+M dH)H \, dB = \mu_0 H (dM + M \, dH), where μ0\mu_0 is the permeability of free space (in SI units; often omitted in cgs for simplicity). Over a complete cycle, the term ∮μ0M dH\oint \mu_0 M \, dH vanishes due to the closed path, leaving W=μ0∮H dMW = \mu_0 \oint H \, dM, or simply ∮H dM\oint H \, dM in normalized units. This area scales with Hc2H_c^2 in simple models, linking coercivity to practical losses in devices like transformers. The temperature dependence of coercivity follows an empirical form Hc(T)≈Hc(0)[1−(TTc)n]H_c(T) \approx H_c(0) \left[1 - \left(\frac{T}{T_c}\right)^n \right], where TcT_c is the Curie temperature and n≈0.77n \approx 0.77 for many ferromagnets, reflecting the softening of anisotropy and exchange interactions with rising temperature. This relation, akin to Kneller's law for permanent magnets, predicts a near-linear drop near T=0T=0 but accelerates toward TcT_c, with deviations observed in nanostructured materials due to surface effects. Experimental loops at elevated temperatures show shrinking HcH_c and loop areas, confirming the model's utility for thermal stability assessments. At higher frequencies, hysteresis loops exhibit broadening, with an apparent increase in HcH_c due to eddy current shielding and viscous domain wall motion, altering the loop shape from quasi-static ideals. As frequency rises, minor loops expand in width and area, dissipating more energy via dynamic losses, though the intrinsic HcH_c remains tied to static properties. This effect is pronounced in conductive ferromagnets, where skin depth limits field penetration, leading to tilted loops at gigahertz ranges. Software tools employing the Landau-Lifshitz-Gilbert (LLG) equation simulate hysteresis loops for fitting experimental data, capturing precessional dynamics without full microscopic details. These micromagnetic codes, such as OOMMF or MuMax3, model HcH_c extraction by solving dmdt=−γm×Heff+αm×dmdt\frac{d\mathbf{m}}{dt} = -\gamma \mathbf{m} \times \mathbf{H}_\mathrm{eff} + \alpha \mathbf{m} \times \frac{d\mathbf{m}}{dt} for discretized spins, enabling parameter optimization like anisotropy constants from loop shapes.

Theoretical Foundations

Classical Mechanisms

Classical mechanisms of coercivity in ferromagnetic materials primarily arise from processes at the domain level, where the reversal of magnetization is governed by the motion of domain walls and the coherent rotation of magnetization within single domains. These foundational theories, developed in the mid-20th century, explain how microstructural features and applied fields influence the field required to reverse the magnetization direction. In soft magnetic materials, low coercivity stems from facile domain wall motion, while hard magnets exhibit high coercivity due to impediments to this motion or rotation. One key classical mechanism is the pinning of domain walls by defects such as inclusions, grain boundaries, or dislocations during magnetization reversal. Domain walls, transitional regions between magnetic domains, possess an energy γw\gamma_w associated with exchange and anisotropy contributions, and their width δ\delta is typically on the order of tens of nanometers. The pinning field HpH_p, representing the coercive field contribution from this mechanism, is given by the expression for the maximum field to unpin a wall from a defect: Hp=2γwμ0MsδH_p = \frac{2\gamma_w}{\mu_0 M_s \delta} where μ0\mu_0 is the permeability of free space and MsM_s is the saturation magnetization. This formula derives from the balance between the Zeeman energy gained by wall motion and the increase in wall energy due to pinning sites, as originally conceptualized in early models of heterogeneous pinning. In materials with abundant defects, such as polycrystalline alloys, this pinning dominates, leading to higher coercivity as the density of pinning sites increases. In contrast, for single-domain particles where domain walls are absent, coercivity arises from the coherent rotation of the magnetization vector, as described by the Stoner-Wohlfarth model. This model assumes uniform rotation of the magnetization in a uniaxial anisotropic particle under an applied field at angle θ\theta to the easy axis. The coercivity HcH_c for field alignment along the easy axis (θ=0\theta = 0) is Hc=2Kμ0MsH_c = \frac{2K}{\mu_0 M_s}, where KK is the anisotropy constant. For oblique fields, it exhibits angular dependence, such as Hc(θ)∝cos⁡(2θ)H_c(\theta) \propto \cos(2\theta) near the easy axis, reflecting the astroid-shaped switching curve in the hysteresis loop. This mechanism is particularly relevant for fine particles or elongated shapes where single-domain states minimize magnetostatic energy, yielding remanence ratios Mr/MsM_r / M_s up to 0.87 for aligned particles. Coercivity mechanisms differ markedly between soft and hard magnets: in soft materials, reversal initiates via easy nucleation of reverse domains at low fields due to weak pinning or low anisotropy, resulting in Hc<1H_c < 1 kA/m; in hard magnets, strong pinning at defects suppresses wall motion post-nucleation, sustaining high Hc>100H_c > 100 kA/m until the field overcomes the barriers. This nucleation-pinning duality resolves historical debates on reversal processes, with nucleation controlling initial reversal in soft phases and pinning dictating overall coercivity in composites or hard alloys. Microstructure profoundly influences these mechanisms, with grain size dd playing a central role akin to the Hall-Petch relation in mechanical properties. In polycrystalline magnets, smaller grains increase grain boundary density, enhancing pinning and thus coercivity via Hc∝1/dH_c \propto 1/\sqrt{d}
Add your contribution
Related Hubs
User Avatar
No comments yet.