Recent from talks
Nothing was collected or created yet.
Demagnetizing field
View on Wikipedia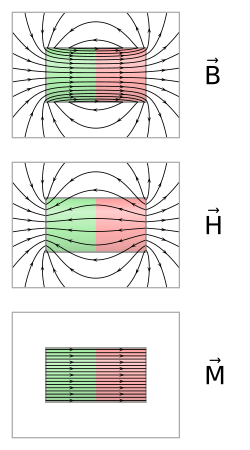
| Electromagnetism |
|---|
 |
The demagnetizing field, also called the stray field (outside the magnet), is the magnetic field (H-field)[1] generated by the magnetization in a magnet. The total magnetic field in a region containing magnets is the sum of the demagnetizing fields of the magnets and the magnetic field due to any free currents or displacement currents. The term demagnetizing field reflects its tendency to act on the magnetization so as to reduce the total magnetic moment. It gives rise to shape anisotropy in ferromagnets with a single magnetic domain and to magnetic domains in larger ferromagnets.
The demagnetizing field of an arbitrarily shaped object requires a numerical solution of Poisson's equation even for the simple case of uniform magnetization. For the special case of ellipsoids (including infinite cylinders) the demagnetization field is linearly related to the magnetization by a geometry dependent constant called the demagnetizing factor. Since the magnetization of a sample at a given location depends on the total magnetic field at that point, the demagnetization factor must be used in order to accurately determine how a magnetic material responds to a magnetic field. (See magnetic hysteresis.)
Magnetostatic principles
[edit]Maxwell's equations
[edit]In general the demagnetizing field is a function of position H(r). It is derived from the magnetostatic equations for a body with no electric currents.[2] These are Ampère's law
| [3] | 1 |
and Gauss's law
| [4] | 2 |
The magnetic field and flux density are related by[5][6]
| [7] | 3 |
where is the permeability of vacuum and M is the magnetisation.
The magnetic potential
[edit]The general solution of the first equation can be expressed as the gradient of a scalar potential U(r):
| [5][6] | 4 |
Inside the magnetic body, the potential Uin is determined by substituting (3) and (4) in (2):
| [8] | 5 |
Outside the body, where the magnetization is zero,
| 6 |
At the surface of the magnet, there are two continuity requirements:[5]
- The component of H parallel to the surface must be continuous (no jump in value at the surface).
- The component of B perpendicular to the surface must be continuous.
This leads to the following boundary conditions at the surface of the magnet:
| 7 |
Here n is the surface normal and is the derivative with respect to distance from the surface.[9]
The outer potential Uout must also be regular at infinity: both |r U| and |r2 U| must be bounded as r goes to infinity. This ensures that the magnetic energy is finite.[10] Sufficiently far away, the magnetic field looks like the field of a magnetic dipole with the same moment as the finite body.
Uniqueness of the demagnetizing field
[edit]Any two potentials that satisfy equations (5), (6) and (7), along with regularity at infinity, have identical gradients. The demagnetizing field Hd is the gradient of this potential (equation 4).
Energy
[edit]The energy of the demagnetizing field is completely determined by an integral over the volume V of the magnet:
| 7 |
Suppose there are two magnets with magnetizations M1 and M2. The energy of the first magnet in the demagnetizing field Hd(2) of the second is
| 8 |
The reciprocity theorem states that[9]
| 9 |
Magnetic charge and the pole-avoidance principle
[edit]Formally, the solution of the equations for the potential is
| 10 |
where r′ is the variable to be integrated over the volume of the body in the first integral and the surface in the second, and ∇′ is the gradient with respect to this variable.[9]
Qualitatively, the negative of the divergence of the magnetization − ∇ · M (called a volume pole) is analogous to a bulk bound electric charge in the body while n · M (called a surface pole) is analogous to a bound surface electric charge. Although the magnetic charges do not exist, it can be useful to think of them in this way. In particular, the arrangement of magnetization that reduces the magnetic energy can often be understood in terms of the pole-avoidance principle, which states that the magnetization affects poles by limiting the poles (tries to reduce them as much as possible).[9]
Effect on magnetization
[edit]Single domain
[edit]
One way to remove the magnetic poles inside a ferromagnet is to make the magnetization uniform. This occurs in single-domain ferromagnets. This still leaves the surface poles, so division into domains reduces the poles further[clarification needed]. However, very small ferromagnets are kept uniformly magnetized by the exchange interaction.
The concentration of poles depends on the direction of magnetization (see the figure). If the magnetization is along the longest axis, the poles are spread across a smaller surface, so the energy is lower. This is a form of magnetic anisotropy called shape anisotropy.
Multiple domains
[edit]
If the ferromagnet is large enough, its magnetization can divide into domains. It is then possible to have the magnetization parallel to the surface. Within each domain the magnetization is uniform, so there are no volume poles, but there are surface poles at the interfaces (domain walls) between domains. However, these poles vanish if the magnetic moments on each side of the domain wall meet the wall at the same angle (so that the components n · M are the same but opposite in sign). Domains configured this way are called closure domains.
Demagnetizing factor
[edit]
An arbitrarily shaped magnetic object has a total magnetic field that varies with location inside the object and can be quite difficult to calculate. This makes it very difficult to determine the magnetic properties of a material such as, for instance, how the magnetization of a material varies with the magnetic field. For a uniformly magnetized sphere in a uniform magnetic field H0 the internal magnetic field H is uniform:
| 11 |
where M0 is the magnetization of the sphere and γ is called the demagnetizing factor, which assumes values between 0 and 1, and equals 1/3 for a sphere in SI units.[5][6][11] Note that in cgs units γ assumes values between 0 and 4π.
This equation can be generalized to include ellipsoids having principal axes in x, y, and z directions such that each component has a relationship of the form:[6]
| 12 |
Other important examples are an infinite plate (an ellipsoid with two of its axes going to infinity) which has γ = 1 (SI units) in a direction normal to the plate and zero otherwise and an infinite cylinder (an ellipsoid with one of its axes tending toward infinity with the other two being the same) which has γ = 0 along its axis and 1/2 perpendicular to its axis.[12] The demagnetizing factors are the principal values of the depolarization tensor, which gives both the internal and external values of the fields induced in ellipsoidal bodies by applied electric or magnetic fields.[13] [14] [15]
Notes and references
[edit]- ^ In this article the term 'magnetic field' is used for the magnetic 'H field' while 'magnetic flux density' is used for the magnetic 'B-field'.
- ^ If there are electric currents in the system, they can be calculated separately and added to the solutions of these equations.
- ^ In words, the curl of the magnetic field is zero.
- ^ In words, the divergence of the magnetic flux density is zero.
- ^ a b c d Jackson 1975, chapter 5
- ^ a b c d Nayfeh & Brussel 1985, chapter 9
- ^ SI units are used in this article.
- ^ The symbol ∇2 ≡ ∇ · ∇ is the Laplace operator.
- ^ a b c d Aharoni 1996, chapter 6
- ^ Brown 1962
- ^ Griffiths 1999, chapter 6
- ^ For tables or equations for the magnetizing factors of the general ellipsoid see Osborn, J. A. (1945). "Demagnetizing Factors of the General Ellipsoid" (PDF). Physical Review. 67 (11–12): 351–7. Bibcode:1945PhRv...67..351O. doi:10.1103/PhysRev.67.351.
- ^ Solivérez, C. E. (1981). "Magnetostatics of Anisotropic Ellipsoidal Bodies". IEEE Transactions on Magnetics. 17 (3): 1363–4. Bibcode:1981ITM....17.1363S. doi:10.1109/TMAG.1981.1061200.
- ^ Di Fratta, G. (2016). "The Newtonian Potential and the Demagnetizing Factors of the General Ellipsoid". Proc. R. Soc. A. 472 (2190) 20160197. arXiv:1505.04970. Bibcode:2016RSPSA.47260197D. doi:10.1098/rspa.2016.0197. PMC 4950212. PMID 27436988.
- ^ Solivérez, C. E. (2016). Electrostatics and Magnetostatics of Polarized Ellipsoidal Bodies: The Depolarization Tensor Method (PDF). Free Scientific Information. ISBN 978-987-28304-0-3.
Further reading
[edit]- Aharoni, Amikam (1996). Introduction to the Theory of Ferromagnetism. Clarendon Press. ISBN 978-0-19-851791-7.
- Brown, William Fuller Jr. (1962). Magnetostatic Principles in Ferromagnetism. Interscience.
- Griffiths, David J. (1999). Introduction to Electrodynamics (third ed.). Prentice Hall. ISBN 978-0-13-805326-0.
- Jackson, John David (1975). Classical Electrodynamics (Second ed.). John Wiley & Sons. ISBN 978-0-471-43132-9.
- Nayfeh, Munir H.; Brussel, Morton K. (1985). Electricity and Magnetism. John Wiley & Sons. ISBN 978-0-471-87681-6.
Demagnetizing field
View on GrokipediaFundamental Concepts
Definition and Physical Origin
The demagnetizing field, denoted as , is the magnetic field generated within a magnetized body by its own magnetization , where represents the magnetic dipole moment per unit volume. This field arises due to spatial variations in the magnetization and acts in a direction opposite to , thereby tending to reduce the net magnetization of the material. In essence, quantifies the self-induced opposition to magnetization uniformity within the body, a fundamental aspect of magnetostatics in ferromagnetic and ferrimagnetic materials.[1] The physical origin of the demagnetizing field lies in the effective bound magnetic charges produced by the divergence of the magnetization vector. Specifically, regions of non-uniform create volume magnetic charge densities proportional to , while discontinuities at the material's surfaces generate surface charges given by , where is the outward normal. These bound charges produce a magnetic field analogous to the electric field generated by charge distributions in electrostatics, with the demagnetizing field emerging as the contribution from these internal sources. In uniformly magnetized regions, the volume charge density vanishes, but surface effects dominate, leading to a field that opposes the applied or intrinsic magnetization.[1] The concept of internal magnetic fields arising from magnetization in materials was systematically developed in the 19th century by James Clerk Maxwell in his seminal work A Treatise on Electricity and Magnetism (1873), where he distinguished these self-fields from externally applied magnetic fields, laying the groundwork for modern magnetostatics. Maxwell's formulation emphasized the role of magnetization in generating these internal fields, integrating them into the broader framework of electromagnetic theory. The specific term "demagnetizing field" and its detailed quantification evolved in later works.[4] In some contexts, the demagnetizing field is also referred to as the stray field, particularly emphasizing its internal nature opposing ; however, stray field often denotes the external magnetic field extending beyond the material, which arises from the same sources but influences the surrounding environment rather than directly counteracting the internal magnetization. This terminological usage highlights the demagnetizing field's primary role in limiting the achievable magnetization inside the sample.[5]Relation to Internal and Applied Fields
In magnetostatics, the total magnetic field within a ferromagnetic or paramagnetic material is composed of the externally applied field and the demagnetizing field , such that .[1][6] The magnetic flux density is then given by , where is the permeability of free space and is the magnetization vector.[1][2] This decomposition highlights how acts as an internal correction to the applied field, arising solely from the material's own magnetization.[6] The demagnetizing field is inherently shape- and magnetization-dependent, distinguishing the internal field environment from that in vacuum where only would prevail.[1] Inside the material, reduces the effective field acting on the magnetic moments, often leading to a net that is weaker than .[2] This reduction occurs because originates from bound magnetic charges induced by on the material's surfaces (and potentially volumes in non-uniform cases), creating a self-opposing contribution.[1] Vectorially, is typically antiparallel to , thereby demagnetizing the sample by counteracting the alignment induced by .[6] Its magnitude varies with geometry; for example, in elongated samples such as rods, is stronger when is oriented along the short axis due to higher surface charge density, compared to the long axis where it is minimized.[1] This geometric sensitivity underscores why sample shape is crucial in magnetic measurements and applications.[2] For introductory analysis, these relations assume uniform throughout the material, simplifying calculations via average factors, though actual scenarios often involve spatial variations in and thus .[1][6] Such uniformity approximations are valid for small, single-domain samples but require micromagnetic modeling for larger or multidomain structures.[2]Magnetostatic Principles
Maxwell's Equations in Magnetostatics
In magnetostatics, the behavior of magnetic fields in materials is governed by simplified forms of Maxwell's equations in the absence of time-varying fields and free currents. The magnetic flux density satisfies , reflecting the absence of magnetic monopoles, while the magnetic field strength is irrotational, . These equations hold within magnetized materials where the magnetization plays a key role. The constitutive relation linking the fields is , where is the permeability of free space; this expresses as the sum of contributions from and the intrinsic magnetization .[7][8] Combining with the constitutive relation yields , introducing an auxiliary source term analogous to charge in electrostatics. The divergence of the magnetization, , is interpreted as an effective volume magnetic charge density , which acts as the source for the field inside the material. This formulation treats variations in as generating "bound" magnetic charges that influence the field distribution. At material boundaries or surfaces, discontinuities in produce surface magnetic charge density , where is the outward unit normal to the surface; these surface charges contribute to the boundary conditions for , specifically the normal component discontinuity .[1] The irrotational nature of () implies that is a conservative field, expressible as the negative gradient of a scalar potential in regions without free currents. This property facilitates analytical solutions for the demagnetizing field, which arises from the effective charges and . In the context of magnetized bodies, the total can be decomposed as , where is the applied field and accounts for the internal field due to , satisfying the same governing equations.[9][8]Magnetic Scalar Potential Formulation
In magnetostatics, the magnetic field can be expressed using a magnetic scalar potential in regions where there are no free currents, satisfying . This allows the introduction of such that .[10] Inside a magnetized material, the potential obeys the Poisson equation , where is the magnetization vector. This equation arises from taking the divergence of and using , leading to . Outside the material, where , the equation simplifies to Laplace's equation . The boundary conditions require to be continuous across the material-vacuum interface, while the normal component of experiences a jump discontinuity equal to the normal component of , i.e., , where points outward from the material.[10][1] This formulation bears a close analogy to the electrostatic scalar potential, where the electric field satisfies Poisson's equation with electric charge density . In the magnetic case, the role of is played by , but unlike electrostatics, there are no true magnetic monopoles; the effective "magnetic charge density" integrates to zero over any closed volume due to the divergence theorem and the absence of magnetic monopoles. Surface contributions arise from bound "magnetic charges" at the material boundaries.[10][1] The demagnetizing field , which opposes the magnetization within the material, is specifically the contribution to arising from itself and can be written as , where is the scalar potential solving the above boundary value problem sourced solely by the distribution of . This potential is determined by integrating over volume and surface magnetic charge densities, providing a practical means to compute for given geometries and magnetizations.[1]Uniqueness of the Demagnetizing Field
In magnetostatics, for a fixed magnetization distribution within a finite body, the demagnetizing field is uniquely determined by the equations and , where inside the body and outside, subject to the boundary condition as .[11] This uniqueness holds up to a gauge choice in the magnetic scalar potential , defined by , where the additive constant in is typically fixed by requiring at infinity.[11] The proof proceeds by assuming two solutions and for the same . Their difference then satisfies and throughout space, implying with (Laplace's equation in source-free regions, as the effective magnetic "charges" from and surface terms are identical). The boundary condition requires as . For harmonic functions in unbounded domains with this decay, the maximum principle (or Liouville's theorem applied to bounded harmonic functions) implies that is constant; since , the constant must yield , confirming uniqueness of the field.[12] The far-field boundary condition reflects the dipole-like nature of the field from a finite magnetized body, where at large distances, ensuring the solution is well-behaved and physically appropriate for isolated systems.[13] This mathematical uniqueness underpins the well-posedness of the demagnetizing field problem, eliminating ambiguity in for isolated magnetic bodies and enabling reliable numerical solutions in computational models of magnetostatics.[14]Energy and Stability
The magnetostatic energy arising from the demagnetizing field in a magnetized body is expressed as , where the integral is over the volume of the material, is the magnetization, and is the permeability of free space.[2] This form captures the self-energy of the magnetization due to its interaction with the field it generates. An equivalent expression, derived using Green's theorem and valid over all space, is , where is the magnetic scalar potential associated with ; this highlights the energy stored in the stray field extending beyond the material.[15] This energy expression can be derived from the principle of virtual work in magnetostatics, which states that for reversible, quasi-static processes in the absence of dissipation, the work done satisfies over the volume. When establishing the magnetization incrementally against the self-induced field, the external work required equals the stored magnetostatic self-energy, leading to the factor of to account for the building process and yielding the integral form .[15] The demagnetizing field inherently opposes within the material, as , which ensures that and contributes positively to the total energy. Stability in magnetized systems is governed by the minimization of , driving the magnetization configuration toward arrangements that reduce the magnitude of and thus lower the overall magnetostatic energy.[2] This opposition and energy penalty from enforce a tendency for configurations with minimal effective magnetic "charges," ensuring a unique energy minimum consistent with the uniqueness of .[15] In the broader context of magnetic materials, the total free energy includes contributions from exchange interactions, magnetocrystalline anisotropy, and Zeeman terms from external fields, but the demagnetizing energy provides the dominant long-range contribution that penalizes non-uniform or misaligned magnetizations.[2] Minimizing the full energy functional, with as a key term, determines equilibrium states, underscoring the role of the demagnetizing field in stabilizing macroscopic magnetic behavior.Modeling Approaches
Magnetic Charge and Pole-Avoidance Principle
The demagnetizing field in a magnetized material can be conceptualized using a model of fictitious magnetic charges, which arise from the divergence of the magnetization . In this approach, a volume magnetic charge density is defined as , representing sources where the magnetization diverges, and a surface magnetic charge density as , where is the outward unit normal to the surface.[1][16] These fictitious charges mimic the behavior of electric charges in electrostatics, allowing the demagnetizing field to be calculated analogously to the electric field from a charge distribution via a Coulomb-like law: for a point magnetic charge at position , the field is , where points from to , integrated over the volume and surface charge distributions.[1] This formulation provides an intuitive visualization of as the field produced by these "poles" within and around the material. The model of fictitious magnetic charges was developed in the 19th century, with significant contributions from William Thomson (Lord Kelvin), who advanced the use of magnetic scalar potentials and pole concepts to describe magnetic fields without relying on vector potentials, facilitating early intuitive analyses of magnetization effects.[17] A key insight from this model is the pole-avoidance principle, which states that magnetization configurations in ferromagnetic materials tend to evolve toward arrangements that minimize the density of free magnetic poles, such as through flux closure structures in domains, because free poles generate opposing fields that increase the magnetostatic energy./06%3A_Ferromagnetism/6.01%3A_Introduction) This principle drives the formation of domain patterns that reduce surface and volume pole densities, thereby lowering the demagnetizing energy associated with these fictitious charges.[18] Although useful for estimating demagnetizing effects and understanding qualitative behaviors, the fictitious charge model is approximate, as real magnetism lacks true monopoles—magnetic field lines form closed loops, and isolated poles cannot exist independently, limiting the analogy to electrostatics in scenarios involving dynamic or quantum effects./06%3A_Ferromagnetism/6.01%3A_Introduction)Demagnetizing Factors for Common Shapes
In uniformly magnetized bodies assuming uniform magnetization , the demagnetizing field inside the material is related to by , where is the dimensionless demagnetizing tensor whose diagonal components along principal axes satisfy in SI units.[19] For ellipsoidal shapes, the demagnetizing tensor is diagonal in the principal axis frame, and the components , , (corresponding to semi-axes ) are given by Osborn's classical expressions, which can be computed via the integral formulas for .[20][19] These factors depend solely on the axial ratios and , with . For a sphere (), .[20][19] Demagnetizing factors for common non-ellipsoidal shapes are often derived as limiting cases of ellipsoids or via direct magnetostatic solutions, assuming uniform . The following table summarizes representative values along principal directions:| Shape | Direction | Demagnetizing Factor |
|---|---|---|
| Sphere | Any | 1/3 |
| Infinite cylinder | Longitudinal (axial) | 0 |
| Infinite cylinder | Transverse | 1/2 |
| Thin film (infinite sheet) | Out-of-plane | ≈1 |
| Thin film (infinite sheet) | In-plane | 0 |
















