Hubbry Logo
Core electronCore electronMain
Open search
Core electron
Community hub
Core electron
logo
7 pages, 0 posts
0 subscribers
Be the first to start a discussion here.
Be the first to start a discussion here.
Core electron
Core electron
Core electron
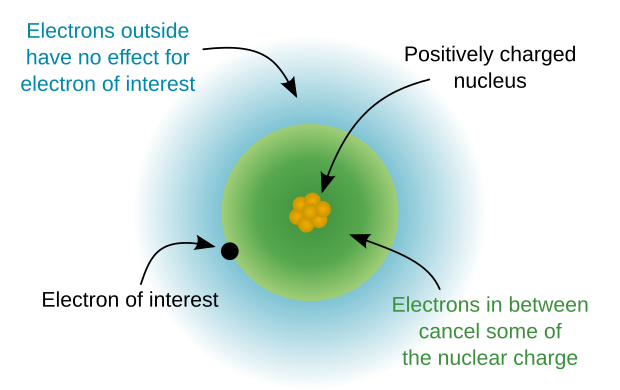
View on Wikipedia
from Wikipedia

Core electrons are the electrons in an atom that are not valence electrons and do not participate as directly in chemical bonding.[1] The nucleus and the core electrons of an atom form the atomic core. Core electrons are tightly bound to the nucleus. Therefore, unlike valence electrons, core electrons play a secondary role in chemical bonding and reactions by screening the positive charge of the atomic nucleus from the valence electrons.[2]

The number of valence electrons of an element can be determined by the periodic table group of the element (see valence electron):

  • For main-group elements, the number of valence electrons ranges from 1 to 8 (ns and np orbitals).
  • For transition metals, the number of valence electrons ranges from 3 to 12 (ns and (n−1)d orbitals).
  • For lanthanides and actinides, the number of valence electrons ranges from 3 to 16 (ns, (n−2)f and (n−1)d orbitals).

All other non-valence electrons for an atom of that element are considered core electrons.

Orbital theory

[edit]

A more complex explanation of the difference between core and valence electrons can be described with atomic orbital theory.[citation needed]

In atoms with a single electron the energy of an orbital is determined exclusively by the principal quantum number n. The n = 1 orbital has the lowest possible energy in the atom. For large n, the energy increases so much that the electron can easily escape from the atom. In single electron atoms, all energy levels with the same principle quantum number are degenerate, and have the same energy.[citation needed]

In atoms with more than one electron, the energy of an electron depends not only on the properties of the orbital it resides in, but also on its interactions with the other electrons in other orbitals. This requires consideration of the ℓ quantum number. Higher values of ℓ are associated with higher values of energy; for instance, the 2p state is higher than the 2s state. When ℓ = 2, the increase in energy of the orbital becomes large enough to push the energy of orbital above the energy of the s-orbital in the next higher shell; when ℓ = 3 the energy is pushed into the shell two steps higher. The filling of the 3d orbitals does not occur until the 4s orbitals have been filled.[citation needed]

The increase in energy for subshells of increasing angular momentum in larger atoms is due to electron–electron interaction effects, and it is specifically related to the ability of low angular momentum electrons to penetrate more effectively toward the nucleus, where they are subject to less screening from the charge of intervening electrons. Thus, in atoms of higher atomic number, the ℓ of electrons becomes more and more of a determining factor in their energy, and the principal quantum numbers n of electrons becomes less and less important in their energy placement. The energy sequence of the first 35 subshells (e.g., 1s, 2s, 2p, 3s, etc.) is given in the following table [not shown?]. Each cell represents a subshell with n and ℓ given by its row and column indices, respectively. The number in the cell is the subshell's position in the sequence. See the periodic table below, organized by subshells. [citation needed]

Periodic Table organized by atomic orbitals.
Periodic Table organized by atomic orbitals.

Atomic core

[edit]
Not to be confused with Atomic nucleus.

The atomic core refers to the central part of the atom excluding the valence electrons.[3] The atomic core has a positive electric charge called the core charge and is the effective nuclear charge experienced by an outer shell electron. In other words, core charge is an expression of the attractive force experienced by the valence electrons to the core of an atom which takes into account the shielding effect of core electrons. Core charge can be calculated by taking the number of protons in the nucleus minus the number of core electrons, also called inner shell electrons, and is always a positive value in neutral atoms.

The mass of the core is almost equal to the mass of the atom. The atomic core can be considered spherically symmetric with sufficient accuracy. The core radius is at least three times smaller than the radius of the corresponding atom (if we calculate the radii by the same methods). For heavy atoms, the core radius grows slightly with increasing number of electrons. The radius of the core of the heaviest naturally occurring element - uranium - is comparable to the radius of a lithium atom, although the latter has only three electrons.

Chemical methods cannot separate the electrons of the core from the atom. When ionized by flame or ultraviolet radiation, atomic cores, as a rule, also remain intact.

Core charge is a convenient way of explaining trends in the periodic table.[4] Since the core charge increases as you move across a row of the periodic table, the outer-shell electrons are pulled more and more strongly towards the nucleus and the atomic radius decreases. This can be used to explain a number of periodic trends such as atomic radius, first ionization energy (IE), electronegativity, and oxidizing.

Core charge can also be calculated as 'atomic number' minus 'all electrons except those in the outer shell'. For example, chlorine (element 17), with electron configuration 1s2 2s2 2p6 3s2 3p5, has 17 protons and 10 inner shell electrons (2 in the first shell, and 8 in the second) so:

Core charge = 17 − 10 = +7

A core charge is the net charge of a nucleus, considering the completed shells of electrons to act as a 'shield.' As a core charge increases, the valence electrons are more strongly attracted to the nucleus, and the atomic radius decreases across the period.

Relativistic effects

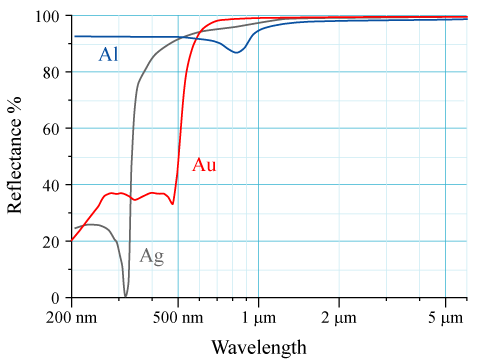
[edit]

For elements with high atomic number Z, relativistic effects can be observed for core electrons. The velocities of core s electrons reach relativistic momentum which leads to contraction of 6s orbitals relative to 5d orbitals. Physical properties affected by these relativistic effects include lowered melting temperature of mercury and the observed golden colour of gold and caesium due to narrowing of energy gap.[5] Gold appears yellow because it absorbs blue light more than it absorbs other visible wavelengths of light and so reflects back yellow-toned light.

Gold Spectrum
Gold Spectrum

Electron transition

[edit]

A core electron can be removed from its core-level upon absorption of electromagnetic radiation. This will either excite the electron to an empty valence shell or cause it to be emitted as a photoelectron due to the photoelectric effect. The resulting atom will have an empty space in the core electron shell, often referred to as a core-hole. It is in a metastable state and will decay within 10−15 s, releasing the excess energy via X-ray fluorescence (as a characteristic X-ray) or by the Auger effect.[6] Detection of the energy emitted by a valence electron falling into a lower-energy orbital provides useful information on the electronic and local lattice structures of a material. Although most of the time this energy is released in the form of a photon, the energy can also be transferred to another electron, which is ejected from the atom. This second ejected electron is called an Auger electron and this process of electronic transition with indirect radiation emission is known as the Auger effect.[7]

Every atom except hydrogen has core-level electrons with well-defined binding energies. It is therefore possible to select an element to probe by tuning the X-ray energy to the appropriate absorption edge. The spectra of the radiation emitted can be used to determine the elemental composition of a material.

See also

[edit]

References

[edit]
Revisions and contributorsEdit on WikipediaRead on Wikipedia

Core electron

View on Grokipedia
from Grokipedia
A core electron is an electron occupying an inner shell or low-energy in an atom, distinct from valence electrons in the outermost shell. These electrons are tightly bound to the nucleus due to their proximity and do not directly participate in chemical bonding or reactions. Core electrons play a pivotal role in atomic structure by providing a , where they reduce the felt by valence electrons through electrostatic repulsion, thereby influencing properties such as , , and across the periodic table. This shielding is most pronounced for inner-shell electrons, as they effectively screen the nucleus from outer electrons while experiencing minimal shielding themselves. Although inert in typical bonding, core electrons are central to advanced spectroscopic techniques, particularly X-ray-based methods like (XPS) and X-ray absorption near-edge structure (XANES), where their excitation or ejection reveals details about an atom's , coordination environment, and local structure in materials. In XPS, for instance, the binding energies of core electrons are measured to identify elemental composition and chemical shifts. In multi-electron atoms, core electrons fill lower shells (n=1, 2, etc.) according to the , forming stable, closed subshells that contribute to the inert nature of and the overall stability of atomic cores. Their relativistic effects become significant in heavy elements, altering orbital energies and influencing phenomena like the .

Basic Concepts

Definition

Core electrons are the electrons in an atom that occupy the inner atomic shells, specifically the K, L, and M shells, which are tightly bound to the nucleus due to their low levels and proximity. These electrons, corresponding to principal quantum numbers n=1n = 1 (K shell), n=2n = 2 (L shell), and n=3n = 3 (M shell), do not participate in chemical bonding because they are shielded from external interactions and remain largely unaffected by neighboring atoms. In , the K shell consists of the 1s orbital, the L shell includes the 2s and 2p orbitals, and the M shell encompasses the 3s, 3p, and 3d orbitals; for lighter elements (up to atomic number around 20), core electrons typically fill orbitals with n<4n < 4. This assignment is based on orbital theory, where electrons occupy discrete energy levels around the nucleus. Core electrons thus form a stable, closed-shell structure that defines the atomic core. A key function of core electrons is to screen the positively charged nucleus from outer electrons, thereby reducing the effective nuclear charge (ZeffZ_{\text{eff}}) felt by valence electrons; Slater's rules provide a qualitative approximation for this shielding, treating core electrons in inner shells as contributing nearly fully (0.85–1.00) to the shielding constant for electrons in the same group or outer groups. For instance, in the neon atom (atomic number 10), the core electrons are 1s21s^2, which shield the valence electrons 2s22p62s^2 2p^6, forming a complete noble gas configuration that serves as the core for elements with higher atomic numbers. In contrast, for heavier elements like gold (atomic number 79, configuration [Xe] 4f14^{14} 5d10^{10} 6s1^1), the core includes electrons up to the 4f orbitals, illustrating how the definition expands with increasing atomic number to encompass more inner shells.

Distinction from Valence Electrons

Core electrons are distinguished from valence electrons primarily by their position in the atomic structure and their involvement in chemical processes. Valence electrons occupy the outermost electron shell of an atom, typically those in the highest principal quantum number (n) or unfilled inner shells for transition metals, and are directly responsible for chemical bonding and the determination of an element's chemical properties. In contrast, core electrons reside in the inner shells closer to the nucleus and do not participate in bonding due to their strong attraction to the nuclear charge. A key physical distinction lies in their binding energies, which reflect the energy required to remove these electrons from the atom. Core electrons exhibit significantly higher binding energies than valence electrons, typically ranging from tens of eV to several keV depending on the shell and atomic number, due to their proximity to the nucleus and effective nuclear charge; for instance, the 1s core electron in a has a binding energy of approximately 284 eV. Valence electrons, however, have much lower binding energies, typically less than 20 eV, corresponding to their ionization potentials, which for elements like carbon range from about 11 eV for the first valence electron. This stark energy difference—often orders of magnitude—makes core electrons tightly bound and stable under normal chemical conditions, while valence electrons are more easily excited or removed. Functionally, core electrons remain inert with respect to chemical reactivity, serving instead as a stable foundation that screens the nucleus and influences atomic spectra through high-energy transitions, whereas valence electrons govern an element's position in the periodic table, its reactivity, and bonding behavior. For example, in sodium (Na), the electron configuration is 1s² 2s² 2p⁶ 3s¹, where the 1s² 2s² 2p⁶ electrons form the core and are chemically inert, while the single 3s¹ valence electron is readily lost to form the Na⁺ ion, exemplifying its role in ionic bonding. This separation underscores how valence electrons dictate periodicity and chemical trends, with the atomic core—comprising the nucleus and core electrons—providing a passive structural backbone.

Theoretical Framework

Orbital Theory

The quantum mechanical description of core electrons begins with the Schrödinger equation for hydrogen-like atoms, which models a single electron orbiting a nucleus of charge ZeZe. The time-independent Schrödinger equation in spherical coordinates is given by −ℏ22m∇2ψ(r,θ,ϕ)−Ze24πϵ0rψ(r,θ,ϕ)=Eψ(r,θ,ϕ),-\frac{\hbar^2}{2m} \nabla^2 \psi(r, \theta, \phi) - \frac{Z e^2}{4\pi \epsilon_0 r} \psi(r, \theta, \phi) = E \psi(r, \theta, \phi), where ψ(r,θ,ϕ)\psi(r, \theta, \phi) is the wave function, mm is the electron mass, and EE is the energy eigenvalue. The solutions, known as atomic orbitals, take the separable form ψn,l,ml(r,θ,ϕ)=Rn,l(r)Yl,ml(θ,ϕ)\psi_{n,l,m_l}(r, \theta, \phi) = R_{n,l}(r) Y_{l,m_l}(\theta, \phi), with the radial function Rn,l(r)R_{n,l}(r) describing the electron's distance from the nucleus and the angular part Yl,ml(θ,ϕ)Y_{l,m_l}(\theta, \phi) given by spherical harmonics. These orbitals form the basis for understanding core electrons, which occupy the lowest principal quantum number nn shells closest to the nucleus. Core orbitals are characterized by four quantum numbers: the principal quantum number nn (a positive integer determining the shell), the azimuthal quantum number ll (ranging from 0 to n−1n-1, with l=0l=0 for s, l=1l=1 for p in inner shells), the magnetic quantum number mlm_l (from −l-l to +l+l), and the spin quantum number msm_s (±1/2\pm 1/2). The Pauli exclusion principle states that no two electrons in an atom can share the same set of all four quantum numbers, limiting each orbital to a maximum of two electrons with opposite spins and restricting subshell occupancy to 2(2l+1)2(2l + 1) electrons (e.g., 2 for 1s, 6 for 2p). In core regions, low nn and ll values dominate, such as the 1s orbital (n=1n=1, l=0l=0), which is fully occupied in atoms beyond hydrogen. The radial probability distribution 4πr2∣Rn,l(r)∣24\pi r^2 |R_{n,l}(r)|^2 for core orbitals shows a high probability density near the nucleus. For the 1s orbital in helium, a representative core electron example, this distribution peaks at approximately 0.13 Å from the nucleus, reflecting the strong nuclear attraction and small spatial extent of inner-shell electrons. This confinement contrasts with valence orbitals, which extend farther out. For multi-electron atoms, the independent-electron approximation of hydrogen-like orbitals is extended using the Hartree-Fock method, which solves self-consistent field equations to account for electron-electron interactions. In this approach, the many-electron wave function is approximated as a of single-particle orbitals, and the effective potential for each electron includes nuclear attraction plus averaged Coulomb and exchange terms from other electrons. Core orbitals, being innermost, experience a nearly bare nuclear potential due to minimal shielding from outer electrons, leading to tight binding. A key feature distinguishing core orbitals is the penetration effect, where s-electrons (l=0l=0) have radial wave functions that extend closer to the nucleus compared to p- or higher-ll orbitals in the same shell, as their probability density does not vanish at r=0r=0. This penetration reduces shielding by inner electrons, increasing the effective nuclear charge ZeffZ_{\text{eff}} and resulting in higher binding energies for core s-electrons relative to non-penetrating orbitals. For instance, in a given shell, the energy ordering follows Es<Ep<EdE_s < E_p < E_d, with core s-orbitals exhibiting the most negative (tightest bound) energies.

Atomic Core

In multi-electron atoms, the atomic core comprises the nucleus, which contains Z protons, and the core electrons occupying the inner electron shells. These core electrons are tightly bound to the nucleus and do not participate in chemical bonding. The presence of core electrons reduces the net positive charge experienced by outer electrons through screening, resulting in an effective nuclear charge given by Zeff=Z−σZ_{\text{eff}} = Z - \sigma, where σ\sigma is the screening constant that accounts for the shielding effect of the inner electrons. For valence electrons, the atomic core functions as a pseudo-nucleus, with its effective charge influencing the behavior of the outer electrons. In alkali metals such as lithium and sodium, the core electrons provide nearly complete screening of the nuclear charge, so the single valence electron perceives an effective charge of approximately +1, akin to the core acting as a point-like positive charge similar to a hydrogen nucleus. The atomic core is characterized by a small radius on the order of a few picometers and exceptionally high electron density near the nucleus, reflecting the compact nature of the inner orbitals. In noble gases like helium, where all electrons occupy core-like orbitals, the core encompasses the entire atom, with helium exhibiting an atomic radius of about 31 pm and concentrated electron density in its 1s shell./Descriptive_Chemistry/Elements_Organized_by_Block/2_p-Block_Elements/Group_18%3A_The_Noble_Gases/1Group_18%3A_Properties_of_Nobel_Gases) This high density contributes to the chemical inertness of noble gases by stabilizing the filled inner shells. Core electrons play a key role in periodic trends, particularly the inert pair effect observed in heavier p-block elements such as thallium and lead. Here, the inner d- and f-orbital core electrons provide incomplete shielding, leading to a higher effective nuclear charge on the outermost ns electrons, which become more tightly bound and less available for bonding, favoring lower oxidation states./08%3A_Chemistry_of_the_Main_Group_Elements/8.06%3A_Group_13_(and_a_note_on_the_post-transition_metals)/8.6.02%3A_Heavier_Elements_of_Group_13_and_the_Inert_Pair_Effect)

Physical Phenomena

Relativistic Effects

In high atomic number (high-Z) atoms, core electrons experience significant relativistic effects due to their high velocities near the nucleus, which approach fractions of the speed of light comparable to 0.1c or higher for inner shells. For instance, the 1s electrons in atoms like mercury (Z=80) achieve average velocities of approximately (Z/137)c ≈ 0.58c, where the factor 137 arises from the inverse of the fine structure constant. This relativistic motion increases the effective electron mass according to the Lorentz factor, m = γ m_0 with γ = 1/√(1 - v²/c²), leading to stronger binding and altered orbital characteristics compared to non-relativistic descriptions. These kinematical effects are most pronounced for s electrons, which have maximum probability density at the nucleus, and become increasingly important for Z > 50. The fundamental theoretical framework for incorporating relativity into atomic structure is provided by the , which describes the relativistic of electrons in the field of the nucleus. For hydrogen-like atoms, the exact energy levels derived from the are given by Enj=mc2[1+(Zαn−(j+1/2)+(j+1/2)2−(Zα)2)2]−1/2,E_{n j} = m c^2 \left[ 1 + \left( \frac{Z \alpha}{n - (j + 1/2) + \sqrt{(j + 1/2)^2 - (Z \alpha)^2}} \right)^2 \right]^{-1/2},
Add your contribution
Related Hubs
User Avatar
No comments yet.