Hubbry Logo
Diffuse reflectionDiffuse reflectionMain
Open search
Diffuse reflection
Community hub
Diffuse reflection
logo
8 pages, 0 posts
0 subscribers
Be the first to start a discussion here.
Be the first to start a discussion here.
Diffuse reflection
Diffuse reflection
Diffuse reflection
View on Wikipedia
from Wikipedia
Diffuse and specular reflection from a glossy surface.[1] The rays represent luminous intensity, which varies according to Lambert's cosine law for an ideal diffuse reflector.

Diffuse reflection is the reflection of light or other waves or particles from a surface such that a ray incident on the surface is scattered at many angles rather than at just one angle as in the case of specular reflection. An ideal diffuse reflecting surface is said to exhibit Lambertian reflection, meaning that there is equal luminance when viewed from all directions lying in the half-space adjacent to the surface.

A surface built from a non-absorbing powder such as plaster, or from fibers such as paper, or from a polycrystalline material such as white marble, reflects light diffusely with great efficiency. Many common materials exhibit a mixture of specular and diffuse reflection.

The visibility of objects, excluding light-emitting ones, is primarily caused by diffuse reflection of light: it is diffusely-scattered light that forms the image of the object in an observer's eye over a wide range of angles of the observer with respect to the object.

Mechanism

[edit]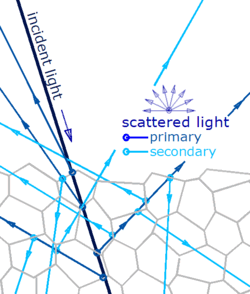
Figure 1 – General mechanism of diffuse reflection by a solid surface (refraction phenomena not represented)
Figure 2 – Diffuse reflection from an irregular surface

Diffuse reflection from solids is generally not due to surface roughness. A flat surface is indeed required to give specular reflection, but it does not prevent diffuse reflection. A piece of highly polished white marble remains white; no amount of polishing will turn it into a mirror. Polishing produces some specular reflection, but the remaining light continues to be diffusely reflected.

The most general mechanism by which a surface gives diffuse reflection does not involve exactly the surface: most of the light is contributed by scattering centers beneath the surface,[2][3] as illustrated in Figure 1. If one were to imagine that the figure represents snow, and that the polygons are its (transparent) ice crystallites, an impinging ray is partially reflected (a few percent) by the first particle, enters in it, is again reflected by the interface with the second particle, enters in it, impinges on the third, and so on, generating a series of "primary" scattered rays in random directions, which, in turn, through the same mechanism, generate a large number of "secondary" scattered rays, which generate "tertiary" rays, and so forth.[4] All these rays walk through the snow crystallites, which do not absorb light, until they arrive at the surface and exit in random directions.[5] The result is that the light that was sent out is returned in all directions, so that snow is white despite being made of transparent material (ice crystals).

For simplicity, "reflections" are spoken of here, but more generally the interface between the small particles that constitute many materials is irregular on a scale comparable with light wavelength, so diffuse light is generated at each interface, rather than a single reflected ray, but the story can be told the same way.

This mechanism is very general, because almost all common materials are made of "small things" held together. Mineral materials are generally polycrystalline: one can describe them as made of a 3D mosaic of small, irregularly shaped defective crystals. Organic materials are usually composed of fibers or cells, with their membranes and their complex internal structure. And each interface, inhomogeneity or imperfection can deviate, reflect or scatter light, reproducing the above mechanism.

Few materials do not cause diffuse reflection: among these are metals, which do not allow light to enter; gases, liquids, glass, and transparent plastics (which have a liquid-like amorphous microscopic structure); single crystals, such as some gems or a salt crystal; and some very special materials, such as the tissues which make the cornea and the lens of an eye. These materials can reflect diffusely, however, if their surface is microscopically rough, like in a frost glass (Figure 2), or, of course, if their homogeneous structure deteriorates, as in cataracts of the eye lens.

A surface may also exhibit both specular and diffuse reflection, as is the case, for example, of glossy paints as used in home painting, which give also a fraction of specular reflection, while matte paints give almost exclusively diffuse reflection.

Most materials can give some specular reflection, provided that their surface can be polished to eliminate irregularities comparable with the light wavelength (a fraction of a micrometer). Depending on the material and surface roughness, reflection may be mostly specular, mostly diffuse, or anywhere in between. A few materials, like liquids and glasses, lack the internal subdivisions which produce the subsurface scattering mechanism described above, and so give only specular reflection. Among common materials, only polished metals can reflect light specularly with high efficiency, as in aluminum or silver usually used in mirrors. All other common materials, even when perfectly polished, usually give not more than a few percent specular reflection, except in particular cases, such as grazing angle reflection by a lake, or the total reflection of a glass prism, or when structured in certain complex configurations such as the silvery skin of many fish species or the reflective surface of a dielectric mirror. Diffuse reflection can be highly efficient, as in white materials, due to the summing up of the many subsurface reflections.

Colored objects

[edit]

Up to this point white objects have been discussed, which do not absorb light. But the above scheme continues to be valid in the case that the material is absorbent. In this case, diffused rays will lose some wavelengths during their walk in the material, and will emerge colored.

Diffusion affects the color of objects in a substantial manner because it determines the average path of light in the material, and hence to which extent the various wavelengths are absorbed.[6] Red ink looks black when it stays in its bottle. Its vivid color is only perceived when it is placed on a scattering material (e.g. paper). This is so because light's path through the paper fibers (and through the ink) is only a fraction of millimeter long. However, light from the bottle has crossed several centimeters of ink and has been heavily absorbed, even in its red wavelengths.

And, when a colored object has both diffuse and specular reflection, usually only the diffuse component is colored. A cherry reflects diffusely red light, absorbs all other colors and has a specular reflection which is essentially white (if the incident light is white light). This is quite general, because, except for metals, the reflectivity of most materials depends on their refractive index, which varies little with the wavelength (though it is this variation that causes the chromatic dispersion in a prism), so that all colors are reflected nearly with the same intensity.

Importance for vision

[edit]

The vast majority of visible objects are seen primarily by diffuse reflection from their surface.[7][8] Exceptions include objects with polished (specularly reflecting) surfaces, and objects that themselves emit light. Rayleigh scattering is responsible for the blue color of the sky, and Mie scattering for the white color of the water droplets in clouds.

Interreflection

[edit]

Diffuse interreflection is a process whereby light reflected from an object strikes other objects in the surrounding area, illuminating them. Diffuse interreflection specifically describes light reflected from objects which are not shiny or specular. In real life terms what this means is that light is reflected off non-shiny surfaces such as the ground, walls, or fabric, to reach areas not directly in view of a light source. If the diffuse surface is colored, the reflected light is also colored, resulting in similar coloration of surrounding objects.

In 3D computer graphics, diffuse interreflection is an important component of global illumination. There are a number of ways to model diffuse interreflection when rendering a scene. Radiosity and photon mapping are two commonly used methods.

Spectroscopy

[edit]

Diffuse reflectance spectroscopy can be used to determine the absorption spectra of powdered samples in cases where transmission spectroscopy is not feasible. This applies to UV-Vis-NIR spectroscopy or mid-infrared spectroscopy.[9][10]

See also

[edit]

References

[edit]
Revisions and contributorsEdit on WikipediaRead on Wikipedia

Diffuse reflection

View on Grokipedia
from Grokipedia
Diffuse reflection is the scattering of light rays in multiple directions upon encountering a rough or irregular surface, in contrast to where light rays reflect coherently in a single direction from a smooth surface. This phenomenon arises when the surface irregularities are on a scale larger than the of visible , approximately 500 nm, causing each incident ray to reflect according to the law of reflection at microscopic facets but resulting in an overall diffusion of light. Diffuse reflection enables the visibility of color, texture, and shape for most everyday objects, such as paper, wood, or unpolished metal, by illuminating them uniformly regardless of the observer's position. At the fundamental level, diffuse reflection adheres to the law of reflection—where the angle of incidence equals the angle of reflection—for each tiny surface element, but the randomness of these elements leads to the apparent . Ideal diffuse reflectors, known as Lambertian surfaces, exhibit brightness independent of the viewing angle, with the reflected intensity proportional to the cosine of the angle between the incident light direction and the surface normal, as described by : Id=kdIlcos⁡θI_d = k_d I_l \cos \theta, where IdI_d is the diffuse intensity, kdk_d is the diffuse reflectance coefficient, IlI_l is the incident light intensity, and θ\theta is the incidence angle. This model is crucial in fields like photometry, for realistic shading, and understanding natural light interaction with matte materials such as chalk or latex paint. Diffuse reflection plays a key role in human vision and environmental , as it predominates in non-glossy surfaces and contributes to the diffuse component of illumination in scenes. Unlike , which preserves image-forming properties, diffuse reflection does not produce clear images but is essential for revealing surface details under varied conditions. In and , quantifying diffuse reflectance helps in applications ranging from to .

Physical Principles

Definition and Mechanism

Diffuse reflection is the process by which incident light or other electromagnetic waves is scattered from a surface in multiple directions, rather than being reflected at a single angle as occurs in specular reflection from smooth surfaces. This scattering results in the surface appearing uniformly illuminated from various viewing angles, without a distinct highlight or glare. In contrast to specular reflection, where the surface acts like a mirror due to its flatness on the scale of the light's wavelength, diffuse reflection dominates on irregular or textured surfaces. The primary physical mechanism of diffuse reflection on rough surfaces arises from microscopic irregularities that are comparable to or larger than the of the incident , causing each incoming ray to interact with a different local tangent plane or facet on the surface. According to the law of reflection applied locally to these facets, the rays are redirected at varied angles, leading to a broad distribution of scattered that appears random and isotropic. This surface is prevalent in materials with uneven textures, such as matte finishes, where the roughness prevents coherent reflection. In addition to , diffuse reflection can occur through in translucent or opaque materials, where light penetrates the surface, undergoes multiple internal interactions such as refractions, reflections, and diffractions at material boundaries or scattering centers like pigments or particles, and eventually re-emerges in random directions. This mechanism is responsible for the soft, even appearance of materials like or biological tissues, as the light is redistributed via these internal paths before exiting. Several factors influence the extent of diffuse reflection, including surface texture—where matte surfaces enhance compared to glossy ones with partial specular components—material composition, such as the presence of pigments that promote internal , and the angle of incidence, which can alter the proportion of scattered versus direct reflection. Representative examples include and cloth, which scatter broadly due to their fibrous textures, and the lunar , whose fine, irregular particles diffuse sunlight across wide angles, contributing to the Moon's observed brightness. An ideal model of perfect diffuse reflection is , where the reflected radiance is proportional to the cosine of the incidence angle and appears equally bright regardless of viewer position.

Mathematical Modeling

Diffuse reflection is mathematically modeled primarily through the framework, which idealizes the process on rough surfaces. Central to this is , which states that the observed from an ideal diffusely reflecting surface is proportional to the cosine of the angle between the surface normal and the direction to the observer. For a surface illuminated by incident II, the radiance LL is given by L=ρIπL = \frac{\rho I}{\pi}, where ρ\rho is the ; this radiance is independent of the observer direction, ensuring the apparent brightness remains constant regardless of the due to the offsetting effects of and uniform . The ideal Lambertian reflector assumes perfect diffusion, where the reflected radiance appears uniform regardless of the viewing angle, modeling the surface as scattering incident light equally in all directions above the hemisphere. This uniformity arises from energy conservation principles: the total reflected radiant flux Φr\Phi_r equals the albedo ρ\rho times the incident flux Φi\Phi_i, so the exitance M=ρEM = \rho E, with EE as the irradiance. Integrating the radiance over the hemisphere yields the relation M=πLM = \pi L, derived from the hemispherical solid angle integral ∫hemisphereLcos⁡θ dω=L∫02π∫0π/2cos⁡θsin⁡θ dθ dϕ=πL\int_{\text{hemisphere}} L \cos \theta \, d\omega = L \int_0^{2\pi} \int_0^{\pi/2} \cos \theta \sin \theta \, d\theta \, d\phi = \pi L, confirming L=ρEπL = \frac{\rho E}{\pi} for constant radiance LL. This bidirectional reflectance distribution function (BRDF) for a Lambertian surface is simply fr=ρπf_r = \frac{\rho}{\pi}, independent of incident and outgoing directions, enforcing reciprocity and energy conservation. The reflectance factor for diffuse surfaces quantifies overall scattering efficiency as ρ=ΦrΦi\rho = \frac{\Phi_r}{\Phi_i}, the ratio of reflected to incident radiant flux, typically ranging from 0 (perfect absorber) to 1 (perfect reflector) and assuming hemispherical integration for both fluxes. While the Lambertian model provides a foundational , real surfaces often deviate due to microscopic effects like retroreflection (brighter appearance when observer and light source align) or forward scattering, particularly on rough matte materials such as or . Non-Lambertian extensions, such as the Oren-Nayar model, account for these by incorporating parameters and microfacet interreflections without assuming uniform radiance, better fitting empirical measurements for non-grazing angles.

Visual and Material Properties

Diffuse Reflection in Colored Materials

In colored materials such as paints and fabrics, pigments selectively absorb certain wavelengths of visible while diffusely reflecting others, which determines the material's perceived color. For instance, in blue paint, the pigments absorb longer wavelengths like and but reflect shorter wavelengths through diffuse from the rough pigment surfaces and surrounding medium. This selective absorption and diffuse reflection process is fundamental to pigmentary coloration in non-metallic objects. Subsurface scattering plays a key role in enhancing color depth in translucent colored materials like plastics and human skin. Light penetrates the surface, undergoes multiple internal scatterings—often governed by Rayleigh scattering for particles much smaller than the light wavelength or Mie scattering for larger particles—and then exits diffusely, mixing with surface-reflected light to produce a softer, more vibrant appearance. In such materials, this internal diffusion contributes to the overall diffuse reflection by redistributing wavelengths that were not immediately absorbed. A prominent example is in plant leaves, where the pigment absorbs blue and red wavelengths for but diffusely reflects green light, giving leaves their characteristic color. Conversely, white objects achieve their appearance through diffuse reflection of all visible wavelengths nearly equally, as seen in materials containing pigments that scatter light broadly without selective absorption. The size and distribution of pigment particles significantly influence scattering efficiency and color saturation. Smaller particles, typically in the nanoscale range, enhance , leading to higher color purity and saturation by more uniformly dispersing reflected light. Larger particles, on the other hand, promote , which can reduce saturation but increase opacity, as the broader scattering angles dilute the intensity of specific wavelengths. Optimal thus balances these effects to achieve desired color vibrancy in applications like coatings and textiles.

Effects on Surface Appearance

Diffuse reflection plays a crucial role in determining the matte appearance of surfaces, where light is scattered uniformly in multiple directions, resulting in a non-shiny, even illumination that lacks the concentrated highlights characteristic of specular reflection. In contrast, specular reflection from smooth surfaces, such as a mirror, produces a glossy, directed bounce of light, creating sharp images or bright spots. High levels of diffuse reflection, as seen in materials like chalkboards or clay, contribute to this uniform look by distributing reflected light broadly, while the bidirectional reflectance distribution function (BRDF) qualitatively describes how such scattering patterns lead to reduced luster and a more subdued visual texture. The appearance of diffusely reflecting surfaces remains relatively consistent across viewing angles and under varying illumination conditions, maintaining steady brightness without the angle-dependent intensity drops seen in specular cases. However, subtle highlights can emerge on diffuse surfaces due to macro-scale roughness, where larger surface irregularities cause localized specular-like effects within the overall . For instance, achieves its strong diffusive properties through microscopic facets that scatter randomly, preventing clear transmission or reflection, whereas sandpaper's texture similarly promotes diffuse via irregular microfacets. Polishing these materials reduces , thereby decreasing diffuse components and enhancing for a shinier finish. Diffuse scattering also influences the of , simulating tactile textures through patterns of light distribution that convey irregularity without physical contact. Rougher diffuse surfaces often appear flatter overall because interreflections among microfacets brighten shadowed areas, as modeled in approaches like the Oren-Nayar reflectance model, which accounts for this effect in non-Lambertian matte materials. This scattering mimics the uneven feel of rough textures, such as that of untreated or plaster, by creating a soft, non-uniform glow that enhances the sense of depth and graininess in everyday observation.

Perceptual and Environmental Effects

Role in Human Vision

Diffuse reflection plays a fundamental role in human vision by enabling the visibility of matte surfaces through the of incident in multiple directions, allowing reflected rays to reach the observer's eye from a wide range of viewing angles. This prevents the concentration of light into a single direction, as occurs in , thereby facilitating the of surface shape, texture, and fine details without the distracting effects of . For instance, under uniform room lighting, the text on a matte book page becomes discernible because diffuse reflection distributes evenly toward the viewer, supporting clear in everyday environments. Psychophysical experiments demonstrate that under diffuse lighting conditions supports accurate depth discrimination, as the leverages these gradients to infer surface orientation and proximity. The perceptual reliance on diffuse reflection reflects an evolutionary of the human to the prevalent diffuseness of natural lighting environments, such as dappled through canopies, which aids and by reducing the interference of harsh specular highlights. Measurements of natural scenes indicate that lighting diffuseness, quantified by Contrast Energy around 0.5, aligns closely with the 's inherent priors for illumination, optimizing shape-from-shading judgments in ecologically relevant settings. This attunement likely evolved to enhance survival in varied outdoor conditions where diffuse light predominates. However, diffuse reflection has limitations in low-light scenarios, where the scattering of reduces the intensity directed toward the observer compared to more focused reflections, necessitating greater incident for sufficient . In contrast to retroreflective surfaces, which efficiently return to its source and improve detection at night, diffuse surfaces demand higher ambient illumination to achieve comparable perceptual thresholds, as the distributed energy yields weaker signals per viewing direction.

Interreflection Phenomena

Interreflection occurs when , after initial diffuse reflection from one surface, undergoes subsequent diffuse reflections from nearby surfaces, resulting in indirect illumination that propagates throughout an environment. This involves multiple bounces of scattered , where each surface acts both as a reflector and a receiver, altering the local conditions. In scenarios, interreflections lead to color bleeding, where saturated hues from one surface transfer to adjacent areas, and to the softening of by filling occluded regions with bounced . For instance, brightly walls in a can impart a warmer tint to nearby neutral objects, such as a white sphere illuminated by ambient hues from surrounding surfaces. Similarly, in concave setups, like the inner surfaces of a folded object, pink interreflections can bleed across boundaries, creating visible color gradients on otherwise uniform areas. To simulate interreflections in , the radiosity method divides a scene into discrete surface patches and iteratively solves a to determine the total outgoing radiance—known as radiosity—from each patch, incorporating emission, reflection, and geometric form factors that quantify energy exchange between patches. This view-independent approach captures diffuse inter-object light transfers efficiently for complex environments, assuming . Real-world examples of interreflections are evident in enclosed spaces, such as rooms where diffuse bounces from walls and floors create even ambient illumination, or in clustered objects like fruits in a , where curved surfaces cause mutual color transfers and enhanced subsurface effects through repeated .

Scientific and Practical Applications

Diffuse Reflectance Spectroscopy

Diffuse reflectance spectroscopy (DRS) is an analytical technique that measures the spectrum of diffusely reflected light from a sample to infer its , physical properties, and structural characteristics, particularly for opaque, powdered, or turbid materials. By illuminating the sample with broadband light and collecting the scattered radiation, DRS captures interactions such as absorption and that reveal molecular signatures without requiring like dissolution or thin-film formation. This method is grounded in the principles of multiple light within the sample, where incident photons undergo repeated reflections and refractions before detection. The cornerstone of quantitative DRS for turbid media is the Kubelka-Munk , originally formulated in 1931 as a simplified model for in layered, scattering-absorbing materials like paints and papers. Derived from the equation using a two-flux —assuming forward and backward diffuse fluxes—this treats the medium as homogeneous and isotropic, solving for steady-state light intensity via differential equations that balance absorption, , and boundary conditions. The resulting Kubelka-Munk function relates measured to optical coefficients: F(R)=(1−R)22R=KSF(R) = \frac{(1 - R)^2}{2R} = \frac{K}{S} Here, RR is the absolute diffuse reflectance (ratio of reflected to incident flux), KK is the absorption coefficient (proportional to chromophore concentration), and SS is the scattering coefficient (dependent on particle size and refractive index differences). This relation enables the transformation of reflectance data into pseudo-absorbance values for direct comparison with transmission spectra, facilitating multicomponent analysis via linear regression or chemometrics. DRS finds extensive use in scientific applications for material characterization. In geology, it identifies minerals and rock compositions by matching spectral features in the visible-near-infrared range to known libraries, enabling rapid, non-destructive field or lab analysis of ores and sediments. In pharmaceuticals, DRS supports quality control of solid dosage forms, such as tablets and powders, by quantifying active ingredients and excipients through partial least squares modeling of reflectance spectra, ensuring uniformity without invasive sampling. For remote sensing of vegetation health, DRS principles underpin indices like the Normalized Difference Vegetation Index (NDVI), calculated as NDVI=RNIR−RredRNIR+Rred\text{NDVI} = \frac{R_{\text{NIR}} - R_{\text{red}}}{R_{\text{NIR}} + R_{\text{red}}}, where higher values indicate robust chlorophyll content and biomass via enhanced near-infrared diffuse reflectance from healthy leaves. Recent advances as of 2025 include the integration of with DRS for clinical tissue differentiation and early detection by assessing tissue oxygenation and blood flow. Additionally, the ISO 23698:2024 standard introduces hybrid (HDRS) for safer, faster efficacy testing, using high-resolution spectra to evaluate protection factors . Key instrumentation in DRS involves an , a hollow enclosure coated with a highly reflective, diffuse material (e.g., or ) that uniformly redistributes incident and scattered light through multiple internal reflections, achieving near-Lambertian illumination and collection efficiency up to 98%. The sphere's ports allow sample placement, monochromatic illumination (via spectrometer), and total detection, often with a reference standard for calibration. Compared to transmission spectroscopy, DRS with integrating spheres excels for opaque samples by avoiding pathlength limitations, enabling in situ measurements on irregular or bulk materials, and providing higher signal-to-noise ratios for low-concentration analytes in scattering matrices.

Applications in Imaging and Technology

In computer graphics, diffuse reflection is modeled using algorithms like the Phong reflection model, which approximates the scattering of light on rough surfaces to achieve realistic shading in rendered images. Developed by Bui Tuong Phong in 1975, this model combines ambient, diffuse, and specular components, with the diffuse term enabling uniform illumination independent of viewer angle, widely applied in video games and simulations for lifelike material appearances. For more accurate representation of non-Lambertian surfaces, the Oren-Nayar model extends diffuse reflection by accounting for surface roughness through microfacet geometry, improving realism in scenes with matte objects like plaster or concrete, as detailed in their 1994 SIGGRAPH paper. These models rely on principles of uniform light scattering to simulate Lambertian-like behavior, ensuring consistent shading across viewpoints. In , diffusers such as softboxes harness diffuse reflection to soften harsh sources, spreading illumination evenly over subjects to minimize specular highlights and shadows. By bouncing off internal reflective surfaces and filtering it through translucent fabric, softboxes create a larger apparent source that promotes broad , ideal for and product photography. Similarly, matte projector screens employ diffuse reflection to scatter projected uniformly, reducing glare and hotspots for consistent image quality across wide viewing angles in presentation environments. Liquid crystal displays (LCDs) incorporate diffuse layers in their backlights to achieve uniform light distribution, where optical films scatter LED or CCFL emissions to eliminate hot spots and ensure even illumination across the panel for consistent viewing. This diffusion enhances color accuracy and brightness uniformity, critical for consumer electronics like televisions and monitors. E-ink technology, used in electronic paper devices, leverages diffuse reflection of ambient light without a backlight, mimicking paper's scattering properties for high readability in sunlight while consuming power only during image updates, thus enabling low-energy operation. Retroreflective paints for road safety markings incorporate mild diffuse reflection alongside primary retroreflection, scattering some broadly to maintain daytime visibility while directing headlights back to drivers at night, as seen in applications on traffic signs and pavement. In , post-processing techniques like media blasting or chemical smoothing optimize surfaces for diffuse finishes, reducing specular glare on functional parts such as prototypes or products to improve aesthetic and practical . As of 2025, emerging applications include diffuse reflection in of highly reflective objects using recovery methods based on surface data references, and studies of diffuse scattering on facial surfaces via ray tracing for enhanced biometric or cosmetic analysis. Additionally, diffuse reflection photoelectric sensors are seeing market growth in industrial automation, projected at a 6.1% CAGR through 2032.

References

  1. http://physics.bu.edu/~duffy/PY106/Reflection.html
  2. https://www.asc.ohio-state.edu/humanic.1/p1201lecture15.pdf
  3. https://physics.highpoint.edu/~jregester/potl/Waves/Reflection/ReflectionA.htm
  4. https://www.cs.cmu.edu/afs/cs/academic/class/15462-s10/www/lec-slides/lec11.pdf
  5. http://msl.cs.uiuc.edu/vr/node197.html
  6. https://www.sciencedirect.com/topics/engineering/diffuse-reflection
  7. https://micro.magnet.fsu.edu/primer/lightandcolor/reflectionintro.html
  8. http://www.graphics.stanford.edu/papers/subsurface/
  9. https://wp.optics.arizona.edu/jgreivenkamp/wp-content/uploads/sites/11/2019/08/502-11-Radiative-Transfer.pdf
  10. https://www.cs.cmu.edu/~16385/s18/lectures/lecture13.pdf
  11. https://www.oceanopticsbook.info/view/surfaces/lambertian-brdfs
  12. https://ies.org/definitions/reflectance-rho-of-a-surface-or-medium/
  13. https://pmc.ncbi.nlm.nih.gov/articles/PMC5444072/
  14. https://www.pnas.org/doi/10.1073/pnas.1215066110
  15. https://pmc.ncbi.nlm.nih.gov/articles/PMC4236566/
  16. https://cseweb.ucsd.edu/~ravir/6998/papers/p165-hanrahan.pdf
  17. https://opg.optica.org/abstract.cfm?uri=josa-51-9-975
  18. https://pmc.ncbi.nlm.nih.gov/articles/PMC5897488/
  19. https://www.tipure.com/en/-/media/files/tipure/legacy/titanium-dioxide-for-coatings.pdf
  20. https://www.researchgate.net/publication/51181127_Relationship_between_the_size_distribution_of_mineral_pigments_and_color_saturation
  21. https://www.azom.com/article.aspx?ArticleID=22858
  22. https://www.cs.cmu.edu/afs/cs/academic/class/15462-f09/www/lec/lec8.pdf
  23. https://opg.optica.org/ao/abstract.cfm?uri=ao-37-1-130
  24. https://cave.cs.columbia.edu/Statics/publications/pdfs/Nayar_SCIENCE95.pdf
  25. https://www.physicsclassroom.com/class/refln/lesson-1/specular-vs-diffuse-reflection
  26. https://www.khanacademy.org/science/ap-physics-2/x0e2f5a2c:geometric-optics/x0e2f5a2c:reflection-and-mirrors/v/specular-and-diffuse-reflection
  27. https://pubmed.ncbi.nlm.nih.gov/11040949/
  28. https://pmc.ncbi.nlm.nih.gov/articles/PMC4141658/
  29. https://www.sciencedirect.com/science/article/abs/pii/S2352154619300208
  30. https://www.3m.com/3M/en_US/road-safety-us/resources/road-transportation-safety-center-blog/full-story/~/road-signs-retroreflectivity/?storyid=328c8880-941b-4adc-a9f9-46a1cd79e637
  31. https://cg.cs.tsinghua.edu.cn/people/~kun/interreflection/interreflection_paper.pdf
  32. https://docs.mech-mind.net/en/eye-3d-camera/latest/extended-reading/reflection-types.html
  33. https://docs.agi32.com/AGi32/Content/multi_use_forms/Color_Bleed_-_Concepts.htm
  34. http://wp.doc.ic.ac.uk/rgi/wp-content/uploads/sites/74/2016/10/ibr_room_basis_noacm.pdf
  35. https://link.springer.com/content/pdf/10.3758/BF03194461.pdf
  36. http://www.eecs.umich.edu/courses/eecs487/W04/Lectures/radiosity.pdf
  37. https://www.ri.cmu.edu/pub_files/pub1/heckbert_paul_1992_1/heckbert_paul_1992_1.pdf
  38. https://opg.optica.org/abstract.cfm?uri=josa-45-6-419
  39. https://www.cs.cmu.edu/~ILIM/publications/PDFs/SLUnderGLT-IJCV.pdf
  40. https://www.spectroscopyonline.com/view/a-brief-look-at-optical-diffuse-reflection-odr-spectroscopy
  41. https://pubs.acs.org/doi/10.1021/ac0702802
  42. https://www.sciencedirect.com/science/article/pii/S2772883823000286
  43. https://www.mdpi.com/2227-9040/12/11/227
  44. https://plantmethods.biomedcentral.com/articles/10.1186/s13007-023-00981-8
  45. https://www.tandfonline.com/doi/full/10.1080/05704928.2025.2525817
  46. https://www.azooptics.com/Article.aspx?ArticleID=2710
  47. https://www.sgs.com/en-nl/news/2025/10/sgs-launches-iso-23698-2024-hdrs-a-breakthrough-sunscreen-testing-method
  48. https://www.labsphere.com/wp-content/uploads/2021/09/Integrating-Sphere-Theory-and-Applications.pdf
  49. https://www.azooptics.com/Article.aspx?ArticleID=2344
  50. https://users.cs.northwestern.edu/~ago820/cs395/Papers/Phong_1975.pdf
  51. https://cave.cs.columbia.edu/Statics/publications/pdfs/Oren_SIGGRAPH94.pdf
  52. https://photographylife.com/what-are-diffusers-in-photography-and-how-to-use-them
  53. https://www.stewartfilmscreen.com/en/news/ambient-light-reflective-screens-and-the-laws-of-physics-introducing-phantom-halr
  54. https://www.cnet.com/culture/is-lcd-and-led-lcd-hdtv-uniformity-a-problem/
  55. https://www.eink.com/technology.html
  56. https://pmc.ncbi.nlm.nih.gov/articles/PMC7760528/
  57. https://www.spiedigitallibrary.org/conference-proceedings-of-spie/13688/1368813/3D-reconstruction-of-highly-reflective-objects-based-on-diffuse-recovery/10.1117/12.3075633.full
  58. https://pmc.ncbi.nlm.nih.gov/articles/PMC11993760/
  59. https://www.linkedin.com/pulse/global-diffuse-reflection-photoelectric-sensors-m8n8f/
Add your contribution
Related Hubs
User Avatar
No comments yet.