Wave

While waves are ubiquitous features of physical systems, no single definition adequately describes the topic. Examples and descriptions of common characteristics are used as an alternative to a single definition.^[4]: 2 In abstract, waves are the dynamic manifestation of time-dependent field theory analogous to ballistics, the dynamic manifestation of particle mechanics, but this point of view misses the many visually appealing examples of waves like vibrating stringed instruments and fluid ripples.^[5]: 1

Viewed microscopically, waves are changes in the value of physical property at a point in space that results from a delayed response to changes in adjacent regions. Examples of properties include pressure, temperature, height, or gravitational force. A physical medium, like vacuum, air, water, or solid rock may exhibit waves in different properties which may or may not be related. Properties like the heights spectators at a sporting event or the level of anxiety among political protestors may also be considered waves when the property depends upon delayed responds to physically adjacent events.^[5]: 2

In physics, a physical quantity that has a value at points in space is called a field, so a wave is disturbance in a field resulting from delayed response to adjacent disturbances. Viewed macroscopically, a wave is the dynamic response of a field caused by effects that that can only propagate at a finite speed. Rotation of an electric dipole produce electromagnetic waves and the mutual rotation of binary stars produce gravitational waves, each of which propagate at the speed of light.^[5]: 7

Periodic or sinusoidal waves are useful idealized examples, but the essential neighbor-to-neighbor interaction with delay means wave may propagate in non-linear, granular, or noisy medium which do not produce these ideal results. Temperature waves or chemical reaction waves demonstrate that waves need not be a material displacement.^[5]: 10

A wave can be described as a number field, namely as a function ${\displaystyle F(x,t)}$ where ${\displaystyle x}$ is a position and ${\displaystyle t}$ is a time.

The value of ${\displaystyle x}$ is a point of space, specifically in the region where the wave is defined. In mathematical terms, it is usually a vector in the Cartesian three-dimensional space ${\displaystyle \mathbb {R} ^{3}}$. However, in many cases one can ignore one dimension, and let ${\displaystyle x}$ be a point of the Cartesian plane ${\displaystyle \mathbb {R} ^{2}}$. This is the case, for example, when studying vibrations of a drum skin. One may even restrict ${\displaystyle x}$ to a point of the Cartesian line ${\displaystyle \mathbb {R} }$ – that is, the set of real numbers. This is the case, for example, when studying vibrations in a violin string or recorder. The time ${\displaystyle t}$, on the other hand, is always assumed to be a scalar; that is, a real number.

The value of ${\displaystyle F(x,t)}$ can be any physical quantity of interest assigned to the point ${\displaystyle x}$ that may vary with time. For example, if ${\displaystyle F}$ represents the vibrations inside an elastic solid, the value of ${\displaystyle F(x,t)}$ is usually a vector that gives the current displacement from ${\displaystyle x}$ of the material particles that would be at the point ${\displaystyle x}$ in the absence of vibration. For an electromagnetic wave, the value of ${\displaystyle F}$ can be the electric field vector ${\displaystyle E}$, or the magnetic field vector ${\displaystyle H}$, or any related quantity, such as the Poynting vector ${\displaystyle E\times H}$. In fluid dynamics, the value of ${\displaystyle F(x,t)}$ could be the velocity vector of the fluid at the point ${\displaystyle x}$, or any scalar property like pressure, temperature, or density. In a chemical reaction, ${\displaystyle F(x,t)}$ could be the concentration of some substance in the neighborhood of point ${\displaystyle x}$ of the reaction medium.

For any dimension ${\displaystyle d}$ (1, 2, or 3), the wave's domain is then a subset ${\displaystyle D}$ of ${\displaystyle \mathbb {R} ^{d}}$, such that the function value ${\displaystyle F(x,t)}$ is defined for any point ${\displaystyle x}$ in ${\displaystyle D}$. For example, when describing the motion of a drum skin, one can consider ${\displaystyle D}$ to be a disk (circle) on the plane ${\displaystyle \mathbb {R} ^{2}}$ with center at the origin ${\displaystyle (0,0)}$, and let ${\displaystyle F(x,t)}$ be the vertical displacement of the skin at the point ${\displaystyle x}$ of ${\displaystyle D}$ and at time ${\displaystyle t}$.

Waves of the same type are often superposed and encountered simultaneously at a given point in space and time. The properties at that point are the sum of the properties of each component wave at that point. In general, the velocities are not the same, so the wave form will change over time and space.

This section needs expansion with: concept summary. You can help by adding to it. (May 2023)

Sometimes one is interested in a single specific wave. More often, however, one needs to understand large set of possible waves; like all the ways that a drum skin can vibrate after being struck once with a drum stick, or all the possible radar echoes one could get from an airplane that may be approaching an airport.

In some of those situations, one may describe such a family of waves by a function ${\displaystyle F(A,B,\ldots ;x,t)}$ that depends on certain parameters ${\displaystyle A,B,\ldots }$, besides ${\displaystyle x}$ and ${\displaystyle t}$. Then one can obtain different waves – that is, different functions of ${\displaystyle x}$ and ${\displaystyle t}$ – by choosing different values for those parameters.

For example, the sound pressure inside a recorder that is playing a "pure" note is typically a standing wave, that can be written as

${\displaystyle F(A,L,n,c;x,t)=A\left(\cos 2\pi x{\frac {2n-1}{4L}}\right)\left(\cos 2\pi ct{\frac {2n-1}{4L}}\right)}$

The parameter ${\displaystyle A}$ defines the amplitude of the wave (that is, the maximum sound pressure in the bore, which is related to the loudness of the note); ${\displaystyle c}$ is the speed of sound; ${\displaystyle L}$ is the length of the bore; and ${\displaystyle n}$ is a positive integer (1,2,3,...) that specifies the number of nodes in the standing wave. (The position ${\displaystyle x}$ should be measured from the mouthpiece, and the time ${\displaystyle t}$ from any moment at which the pressure at the mouthpiece is maximum. The quantity ${\displaystyle \lambda =4L/(2n-1)}$ is the wavelength of the emitted note, and ${\displaystyle f=c/\lambda }$ is its frequency.) Many general properties of these waves can be inferred from this general equation, without choosing specific values for the parameters.

As another example, it may be that the vibrations of a drum skin after a single strike depend only on the distance ${\displaystyle r}$ from the center of the skin to the strike point, and on the strength ${\displaystyle s}$ of the strike. Then the vibration for all possible strikes can be described by a function ${\displaystyle F(r,s;x,t)}$.

Sometimes the family of waves of interest has infinitely many parameters. For example, one may want to describe what happens to the temperature in a metal bar when it is initially heated at various temperatures at different points along its length, and then allowed to cool by itself in vacuum. In that case, instead of a scalar or vector, the parameter would have to be a function ${\displaystyle h}$ such that ${\displaystyle h(x)}$ is the initial temperature at each point ${\displaystyle x}$ of the bar. Then the temperatures at later times can be expressed by a function ${\displaystyle F}$ that depends on the function ${\displaystyle h}$ (that is, a functional operator), so that the temperature at a later time is ${\displaystyle F(h;x,t)}$

Another way to describe and study a family of waves is to give a mathematical equation that, instead of explicitly giving the value of ${\displaystyle F(x,t)}$, only constrains how those values can change with time. Then the family of waves in question consists of all functions ${\displaystyle F}$ that satisfy those constraints – that is, all solutions of the equation.

This approach is extremely important in physics, because the constraints usually are a consequence of the physical processes that cause the wave to evolve. For example, if ${\displaystyle F(x,t)}$ is the temperature inside a block of some homogeneous and isotropic solid material, its evolution is constrained by the partial differential equation

${\displaystyle {\frac {\partial F}{\partial t}}(x,t)=\alpha \left({\frac {\partial ^{2}F}{\partial x_{1}^{2}}}(x,t)+{\frac {\partial ^{2}F}{\partial x_{2}^{2}}}(x,t)+{\frac {\partial ^{2}F}{\partial x_{3}^{2}}}(x,t)\right)+\beta Q(x,t)}$

where ${\displaystyle Q(p,f)}$ is the heat that is being generated per unit of volume and time in the neighborhood of ${\displaystyle x}$ at time ${\displaystyle t}$ (for example, by chemical reactions happening there); ${\displaystyle x_{1},x_{2},x_{3}}$ are the Cartesian coordinates of the point ${\displaystyle x}$; ${\displaystyle \partial F/\partial t}$ is the (first) derivative of ${\displaystyle F}$ with respect to ${\displaystyle t}$; and ${\displaystyle \partial ^{2}F/\partial x_{i}^{2}}$ is the second derivative of ${\displaystyle F}$ relative to ${\displaystyle x_{i}}$. (The symbol "${\displaystyle \partial }$" is meant to signify that, in the derivative with respect to some variable, all other variables must be considered fixed.)

This equation can be derived from the laws of physics that govern the diffusion of heat in solid media. For that reason, it is called the heat equation in mathematics, even though it applies to many other physical quantities besides temperatures.

For another example, we can describe all possible sounds echoing within a container of gas by a function ${\displaystyle F(x,t)}$ that gives the pressure at a point ${\displaystyle x}$ and time ${\displaystyle t}$ within that container. If the gas was initially at uniform temperature and composition, the evolution of ${\displaystyle F}$ is constrained by the formula

${\displaystyle {\frac {\partial ^{2}F}{\partial t^{2}}}(x,t)=\alpha \left({\frac {\partial ^{2}F}{\partial x_{1}^{2}}}(x,t)+{\frac {\partial ^{2}F}{\partial x_{2}^{2}}}(x,t)+{\frac {\partial ^{2}F}{\partial x_{3}^{2}}}(x,t)\right)+\beta P(x,t)}$

Here ${\displaystyle P(x,t)}$ is some extra compression force that is being applied to the gas near ${\displaystyle x}$ by some external process, such as a loudspeaker or piston right next to ${\displaystyle p}$.

This same differential equation describes the behavior of mechanical vibrations and electromagnetic fields in a homogeneous isotropic non-conducting solid. Note that this equation differs from that of heat flow only in that the left-hand side is ${\displaystyle \partial ^{2}F/\partial t^{2}}$, the second derivative of ${\displaystyle F}$ with respect to time, rather than the first derivative ${\displaystyle \partial F/\partial t}$. Yet this small change makes a huge difference on the set of solutions ${\displaystyle F}$. This differential equation is called "the" wave equation in mathematics, even though it describes only one very special kind of waves.

Consider a traveling transverse wave (which may be a pulse) on a string (the medium). Consider the string to have a single spatial dimension. Consider this wave as traveling

• in the ${\displaystyle x}$ direction in space. For example, let the positive ${\displaystyle x}$ direction be to the right, and the negative ${\displaystyle x}$ direction be to the left.
• with constant amplitude ${\displaystyle u}$
• with constant velocity ${\displaystyle v}$, where ${\displaystyle v}$ is
  • independent of wavelength (no dispersion)
  • independent of amplitude (linear media, not nonlinear).^[6][7]
• with constant waveform, or shape

This wave can then be described by the two-dimensional functions

or, more generally, by d'Alembert's formula:^[8] $${\displaystyle u(x,t)=F(x-vt)+G(x+vt).}$$ representing two component waveforms ${\displaystyle F}$ and ${\displaystyle G}$ traveling through the medium in opposite directions. A generalized representation of this wave can be obtained^[9] as the partial differential equation $${\displaystyle {\frac {1}{v^{2}}}{\frac {\partial ^{2}u}{\partial t^{2}}}={\frac {\partial ^{2}u}{\partial x^{2}}}.}$$

General solutions are based upon Duhamel's principle.^[10]

The form or shape of F in d'Alembert's formula involves the argument x − vt. Constant values of this argument correspond to constant values of F, and these constant values occur if x increases at the same rate that vt increases. That is, the wave shaped like the function F will move in the positive x-direction at velocity v (and G will propagate at the same speed in the negative x-direction).^[11]

In the case of a periodic function F with period λ, that is, F(x + λ − vt) = F(x − vt), the periodicity of F in space means that a snapshot of the wave at a given time t finds the wave varying periodically in space with period λ (the wavelength of the wave). In a similar fashion, this periodicity of F implies a periodicity in time as well: F(x − v(t + T)) = F(x − vt) provided vT = λ, so an observation of the wave at a fixed location x finds the wave undulating periodically in time with period T = λ/v.^[12]

The amplitude of a wave may be constant (in which case the wave is a c.w. or continuous wave), or may be modulated so as to vary with time and/or position. The outline of the variation in amplitude is called the envelope of the wave. Mathematically, the modulated wave can be written in the form:^[13][14][15] $${\displaystyle u(x,t)=A(x,t)\sin \left(kx-\omega t+\phi \right),}$$ where ${\displaystyle A(x,\ t)}$ is the amplitude envelope of the wave, ${\displaystyle k}$ is the wavenumber and ${\displaystyle \phi }$ is the phase. If the group velocity ${\displaystyle v_{g}}$ (see below) is wavelength-independent, this equation can be simplified as:^[16] $${\displaystyle u(x,t)=A(x-v_{g}t)\sin \left(kx-\omega t+\phi \right),}$$ showing that the envelope moves with the group velocity and retains its shape. Otherwise, in cases where the group velocity varies with wavelength, the pulse shape changes in a manner often described using an envelope equation.^[16][17]

There are two velocities that are associated with waves, the phase velocity and the group velocity.

Phase velocity is the rate at which the phase of the wave propagates in space: any given phase of the wave (for example, the crest) will appear to travel at the phase velocity. The phase velocity is given in terms of the wavelength λ (lambda) and period T as $${\displaystyle v_{\mathrm {p} }={\frac {\lambda }{T}}.}$$

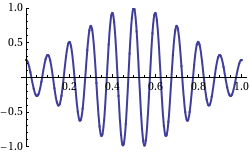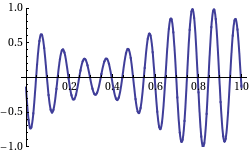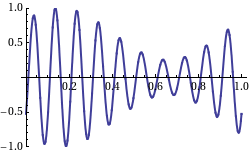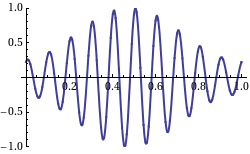
Group velocity is a property of waves that have a defined envelope, measuring propagation through space (that is, phase velocity) of the overall shape of the waves' amplitudes—modulation or envelope of the wave.

This section is an excerpt from Sine wave.[edit]

A sine wave, sinusoidal wave, or sinusoid (symbol: ∿) is a periodic wave whose waveform (shape) is the trigonometric sine function. In mechanics, as a linear motion over time, this is simple harmonic motion; as rotation, it corresponds to uniform circular motion. Sine waves occur often in physics, including wind waves, sound waves, and light waves, such as monochromatic radiation. In engineering, signal processing, and mathematics, Fourier analysis decomposes general functions into a sum of sine waves of various frequencies, relative phases, and magnitudes.

When any two sine waves of the same frequency (but arbitrary phase) are linearly combined, the result is another sine wave of the same frequency; this property is unique among periodic waves. Conversely, if some phase is chosen as a zero reference, a sine wave of arbitrary phase can be written as the linear combination of two sine waves with phases of zero and a quarter cycle, the sine and cosine components, respectively.

A plane wave is a kind of wave whose value varies only in one spatial direction. That is, its value is constant on a plane that is perpendicular to that direction. Plane waves can be specified by a vector of unit length ${\displaystyle {\hat {n}}}$ indicating the direction that the wave varies in, and a wave profile describing how the wave varies as a function of the displacement along that direction (${\displaystyle {\hat {n}}\cdot {\vec {x}}}$) and time (${\displaystyle t}$). Since the wave profile only depends on the position ${\displaystyle {\vec {x}}}$ in the combination ${\displaystyle {\hat {n}}\cdot {\vec {x}}}$, any displacement in directions perpendicular to ${\displaystyle {\hat {n}}}$ cannot affect the value of the field.

Plane waves are often used to model electromagnetic waves far from a source. For electromagnetic plane waves, the electric and magnetic fields themselves are transverse to the direction of propagation, and also perpendicular to each other.

A standing wave, also known as a stationary wave, is a wave whose envelope remains in a constant position. This phenomenon arises as a result of interference between two waves traveling in opposite directions.

The sum of two counter-propagating waves (of equal amplitude and frequency) creates a standing wave. Standing waves commonly arise when a boundary blocks further propagation of the wave, thus causing wave reflection, and therefore introducing a counter-propagating wave. For example, when a violin string is displaced, transverse waves propagate out to where the string is held in place at the bridge and the nut, where the waves are reflected back. At the bridge and nut, the two opposed waves are in antiphase and cancel each other, producing a node. Halfway between two nodes there is an antinode, where the two counter-propagating waves enhance each other maximally. There is no net propagation of energy over time.

• 
  One-dimensional standing waves; the fundamental mode and the first 5 overtones
• 
  A two-dimensional standing wave on a disk; this is the fundamental mode.
• 
  A standing wave on a disk with two nodal lines crossing at the center; this is an overtone.

A soliton or solitary wave is a self-reinforcing wave packet that maintains its shape while it propagates at a constant velocity. Solitons are caused by a cancellation of nonlinear and dispersive effects in the medium. (Dispersive effects are a property of certain systems where the speed of a wave depends on its frequency.) Solitons are the solutions of a widespread class of weakly nonlinear dispersive partial differential equations describing physical systems.

Wave propagation is any of the ways in which waves travel. With respect to the direction of the oscillation relative to the propagation direction, we can distinguish between longitudinal wave and transverse waves.

Electromagnetic waves propagate in vacuum as well as in material media. Propagation of other wave types such as sound may occur only in a transmission medium.

The propagation and reflection of plane waves—e.g. Pressure waves (P wave) or Shear waves (SH or SV-waves) are phenomena that were first characterized within the field of classical seismology, and are now considered fundamental concepts in modern seismic tomography. The analytical solution to this problem exists and is well known. The frequency domain solution can be obtained by first finding the Helmholtz decomposition of the displacement field, which is then substituted into the wave equation. From here, the plane wave eigenmodes can be calculated.^{[citation needed][clarification needed]}

The analytical solution of SV-wave in a half-space indicates that the plane SV wave reflects back to the domain as a P and SV waves, leaving out special cases. The angle of the reflected SV wave is identical to the incidence wave, while the angle of the reflected P wave is greater than the SV wave. For the same wave frequency, the SV wavelength is smaller than the P wavelength. This fact has been depicted in this animated picture.^[18]

Similar to the SV wave, the P incidence, in general, reflects as the P and SV wave. There are some special cases where the regime is different.^{[clarification needed]}

Wave velocity is a general concept, of various kinds of wave velocities, for a wave's phase and speed concerning energy (and information) propagation. The phase velocity is given as: $${\displaystyle v_{\rm {p}}={\frac {\omega }{k}},}$$ where:

• v_p is the phase velocity (with SI unit m/s),
• ω is the angular frequency (with SI unit rad/s),
• k is the wavenumber (with SI unit rad/m).

The phase speed gives you the speed at which a point of constant phase of the wave will travel for a discrete frequency. The angular frequency ω cannot be chosen independently from the wavenumber k, but both are related through the dispersion relationship: $${\displaystyle \omega =\Omega (k).}$$

In the special case Ω(k) = ck, with c a constant, the waves are called non-dispersive, since all frequencies travel at the same phase speed c. For instance electromagnetic waves in vacuum are non-dispersive. In case of other forms of the dispersion relation, we have dispersive waves. The dispersion relationship depends on the medium through which the waves propagate and on the type of waves (for instance electromagnetic, sound or water waves).

The speed at which a resultant wave packet from a narrow range of frequencies will travel is called the group velocity and is determined from the gradient of the dispersion relation: $${\displaystyle v_{\rm {g}}={\frac {\partial \omega }{\partial k}}}$$

In almost all cases, a wave is mainly a movement of energy through a medium. Most often, the group velocity is the velocity at which the energy moves through this medium.

Waves exhibit common behaviors under a number of standard situations, for example:

Waves normally move in a straight line (that is, rectilinearly) through a transmission medium. Such media can be classified into one or more of the following categories:

• A bounded medium if it is finite in extent, otherwise an unbounded medium
• A linear medium if the amplitudes of different waves at any particular point in the medium can be added
• A uniform medium or homogeneous medium if its physical properties are unchanged at different locations in space
• An anisotropic medium if one or more of its physical properties differ in one or more directions
• An isotropic medium if its physical properties are the same in all directions

Waves are usually defined in media which allow most or all of a wave's energy to propagate without loss. However materials may be characterized as "lossy" if they remove energy from a wave, usually converting it into heat. This is termed "absorption." A material which absorbs a wave's energy, either in transmission or reflection, is characterized by a refractive index which is complex. The amount of absorption will generally depend on the frequency (wavelength) of the wave, which, for instance, explains why objects may appear colored.

When a wave strikes a reflective surface, it changes direction, such that the angle made by the incident wave and line normal to the surface equals the angle made by the reflected wave and the same normal line.

Refraction is the phenomenon of a wave changing its speed. Mathematically, this means that the size of the phase velocity changes. Typically, refraction occurs when a wave passes from one medium into another. The amount by which a wave is refracted by a material is given by the refractive index of the material. The directions of incidence and refraction are related to the refractive indices of the two materials by Snell's law.

A wave exhibits diffraction when it encounters an obstacle that bends the wave or when it spreads after emerging from an opening. Diffraction effects are more pronounced when the size of the obstacle or opening is comparable to the wavelength of the wave.

When waves in a linear medium (the usual case) cross each other in a region of space, they do not actually interact with each other, but continue on as if the other one were not present. However at any point in that region the field quantities describing those waves add according to the superposition principle. If the waves are of the same frequency in a fixed phase relationship, then there will generally be positions at which the two waves are in phase and their amplitudes add, and other positions where they are out of phase and their amplitudes (partially or fully) cancel. This is called an interference pattern.

The phenomenon of polarization arises when wave motion can occur simultaneously in two orthogonal directions. Transverse waves can be polarized, for instance. When polarization is used as a descriptor without qualification, it usually refers to the special, simple case of linear polarization. A transverse wave is linearly polarized if it oscillates in only one direction or plane. In the case of linear polarization, it is often useful to add the relative orientation of that plane, perpendicular to the direction of travel, in which the oscillation occurs, such as "horizontal" for instance, if the plane of polarization is parallel to the ground. Electromagnetic waves propagating in free space, for instance, are transverse; they can be polarized by the use of a polarizing filter.

Longitudinal waves, such as sound waves, do not exhibit polarization. For these waves there is only one direction of oscillation, that is, along the direction of travel.

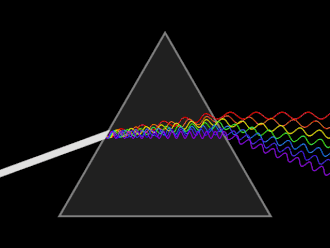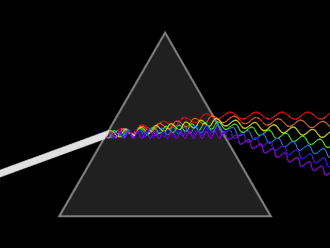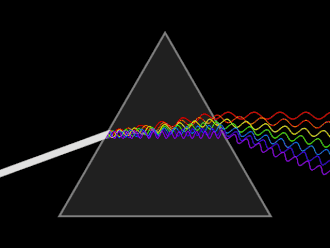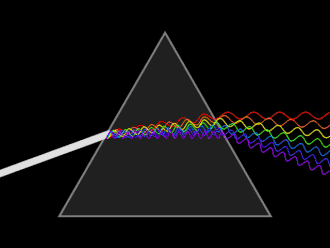
Dispersion is the frequency dependence of the refractive index, a consequence of the atomic nature of materials.^[19]: 67 A wave undergoes dispersion when either the phase velocity or the group velocity depends on the wave frequency. Dispersion is seen by letting white light pass through a prism, the result of which is to produce the spectrum of colors of the rainbow. Isaac Newton was the first to recognize that this meant that white light was a mixture of light of different colors.^[19]: 190

The Doppler effect or Doppler shift is the change in frequency of a wave in relation to an observer who is moving relative to the wave source.^[20] It is named after the Austrian physicist Christian Doppler, who described the phenomenon in 1842.

A mechanical wave is an oscillation of matter, and therefore transfers energy through a medium.^[21] While waves can move over long distances, the movement of the medium of transmission—the material—is limited. Therefore, the oscillating material does not move far from its initial position. Mechanical waves can be produced only in media which possess elasticity and inertia. There are three types of mechanical waves: transverse waves, longitudinal waves, and surface waves.

The transverse vibration of a string is a function of tension and inertia, and is constrained by the length of the string as the ends are fixed. This constraint limits the steady state modes that are possible, and thereby the frequencies. The speed of a transverse wave traveling along a vibrating string (v) is directly proportional to the square root of the tension of the string (T) over the linear mass density (μ):

${\displaystyle v={\sqrt {\frac {T}{\mu }}},}$

where the linear density μ is the mass per unit length of the string.

Acoustic or sound waves are compression waves that propagate through gases, liquids, solids and plasmas. They travel at the speed given by:

${\displaystyle v={\sqrt {\frac {B}{\rho _{0}}}},}$

or the square root of the adiabatic bulk modulus divided by the ambient density of the medium (see speed of sound).

Gravity waves are waves generated in a fluid medium or at the interface between two media when the force of gravity or buoyancy works to restore equilibrium. Surface waves on water are the most familiar example.

• Ripples on the surface of a pond are actually a combination of transverse and longitudinal waves; therefore, the points on the surface follow orbital paths.
• Inertial waves, which occur in rotating fluids and are restored by the Coriolis effect.
• Ocean surface waves, which are perturbations that propagate through water.

Body waves travel through the interior of the medium along paths controlled by the material properties in terms of density and modulus (stiffness). The density and modulus, in turn, vary according to temperature, composition, and material phase. This effect resembles the refraction of light waves. Two types of particle motion result in two types of body waves: Primary and Secondary waves.

Seismic waves are waves of energy that travel through the Earth's layers, and are a result of earthquakes, volcanic eruptions, magma movement, large landslides and large man-made explosions that give out low-frequency acoustic energy. They include body waves—the primary (P waves) and secondary waves (S waves)—and surface waves, such as Rayleigh waves, Love waves, and Stoneley waves.

A shock wave is a type of propagating disturbance. When a wave moves faster than the local speed of sound in a fluid, it is a shock wave. Like an ordinary wave, a shock wave carries energy and can propagate through a medium; however, it is characterized by an abrupt, nearly discontinuous change in pressure, temperature and density of the medium.^[22]

Shear waves are body waves due to shear rigidity and inertia. They can only be transmitted through solids and to a lesser extent through liquids with a sufficiently high viscosity.

Gravitational waves also travel through space. The first observation of gravitational waves was announced on 11 February 2016.^[23] Gravitational waves are disturbances in the curvature of spacetime, predicted by Einstein's theory of general relativity.

• Waves of traffic, that is, propagation of different densities of motor vehicles, and so forth, which can be modeled as kinematic waves^[24][25]
• Metachronal wave refers to the appearance of a traveling wave produced by coordinated sequential actions.

An electromagnetic wave consists of two waves that are oscillations of the electric and magnetic fields. An electromagnetic wave travels in a direction that is at right angles to the oscillation direction of both fields. In the 19th century, James Clerk Maxwell showed that, in vacuum, the electric and magnetic fields satisfy the wave equation both with speed equal to that of the speed of light. From this emerged the idea that light is an electromagnetic wave. The unification of light and electromagnetic waves was experimentally confirmed by Hertz in the end of the 1880s. Electromagnetic waves can have different frequencies (and thus wavelengths), and are classified accordingly in wavebands, such as radio waves, microwaves, infrared, visible light, ultraviolet, X-rays, and gamma rays. The range of frequencies in each of these bands is continuous, and the limits of each band are mostly arbitrary, with the exception of visible light, which must be visible to the normal human eye.

The Schrödinger equation describes the wave-like behavior of particles in quantum mechanics. Solutions of this equation are wave functions which can be used to describe the probability density of a particle.

The Dirac equation is a relativistic wave equation detailing electromagnetic interactions. Dirac waves accounted for the fine details of the hydrogen spectrum in a completely rigorous way. The wave equation also implied the existence of a new form of matter, antimatter, previously unsuspected and unobserved and which was experimentally confirmed. In the context of quantum field theory, the Dirac equation is reinterpreted to describe quantum fields corresponding to spin-1⁄2 particles.

Louis de Broglie postulated that all particles with momentum have a wavelength

${\displaystyle \lambda ={\frac {h}{p}},}$

where h is the Planck constant, and p is the magnitude of the momentum of the particle. This hypothesis was at the basis of quantum mechanics. Nowadays, this wavelength is called the de Broglie wavelength. For example, the electrons in a CRT display have a de Broglie wavelength of about 10⁻¹³ m.

A wave representing such a particle traveling in the k-direction is expressed by the wave function as follows:

${\displaystyle \psi (\mathbf {r} ,\,t=0)=Ae^{i\mathbf {k\cdot r} },}$

where the wavelength is determined by the wave vector k as:

${\displaystyle \lambda ={\frac {2\pi }{k}},}$

and the momentum by:

${\displaystyle \mathbf {p} =\hbar \mathbf {k} .}$

However, a wave like this with definite wavelength is not localized in space, and so cannot represent a particle localized in space. To localize a particle, de Broglie proposed a superposition of different wavelengths ranging around a central value in a wave packet,^[27] a waveform often used in quantum mechanics to describe the wave function of a particle. In a wave packet, the wavelength of the particle is not precise, and the local wavelength deviates on either side of the main wavelength value.

In representing the wave function of a localized particle, the wave packet is often taken to have a Gaussian shape and is called a Gaussian wave packet.^[28][29][30] Gaussian wave packets also are used to analyze water waves.^[31]

For example, a Gaussian wavefunction ψ might take the form:^[32]

${\displaystyle \psi (x,\,t=0)=A\exp \left(-{\frac {x^{2}}{2\sigma ^{2}}}+ik_{0}x\right),}$

at some initial time t = 0, where the central wavelength is related to the central wave vector k₀ as λ₀ = 2π / k₀. It is well known from the theory of Fourier analysis,^[33] or from the Heisenberg uncertainty principle (in the case of quantum mechanics) that a narrow range of wavelengths is necessary to produce a localized wave packet, and the more localized the envelope, the larger the spread in required wavelengths. The Fourier transform of a Gaussian is itself a Gaussian.^[34] Given the Gaussian:

${\displaystyle f(x)=e^{-x^{2}/\left(2\sigma ^{2}\right)},}$

the Fourier transform is:

${\displaystyle {\tilde {f}}(k)=\sigma e^{-\sigma ^{2}k^{2}/2}.}$

The Gaussian in space therefore is made up of waves:

${\displaystyle f(x)={\frac {1}{\sqrt {2\pi }}}\int _{-\infty }^{\infty }\ {\tilde {f}}(k)e^{ikx}\ dk;}$

that is, a number of waves of wavelengths λ such that kλ = 2 π.

The parameter σ decides the spatial spread of the Gaussian along the x-axis, while the Fourier transform shows a spread in wave vector k determined by 1/σ. That is, the smaller the extent in space, the larger the extent in k, and hence in λ = 2π/k.

• Index of wave articles