Incircle and excircles

Suppose ${\displaystyle \triangle ABC}$ has an incircle with radius ${\displaystyle r}$ and center ${\displaystyle I}$. Let ${\displaystyle a}$ be the length of ${\displaystyle {\overline {BC}}}$, ${\displaystyle b}$ the length of ${\displaystyle {\overline {AC}}}$, and ${\displaystyle c}$ the length of ${\displaystyle {\overline {AB}}}$.

Also let ${\displaystyle T_{A}}$, ${\displaystyle T_{B}}$, and ${\displaystyle T_{C}}$ be the touchpoints where the incircle touches ${\displaystyle {\overline {BC}}}$, ${\displaystyle {\overline {AC}}}$, and ${\displaystyle {\overline {AB}}}$.

The incenter is the point where the internal angle bisectors of ${\displaystyle \angle ABC,\angle BCA,{\text{ and }}\angle BAC}$ meet.

The trilinear coordinates for a point in the triangle is the ratio of all the distances to the triangle sides. Because the incenter is the same distance from all sides of the triangle, the trilinear coordinates for the incenter are^[6]

$${\displaystyle \ 1:1:1.}$$

The barycentric coordinates for a point in a triangle give weights such that the point is the weighted average of the triangle vertex positions. Barycentric coordinates for the incenter are given by

$${\displaystyle a:b:c}$$

where ${\displaystyle a}$, ${\displaystyle b}$, and ${\displaystyle c}$ are the lengths of the sides of the triangle, or equivalently (using the law of sines) by

$${\displaystyle \sin A:\sin B:\sin C}$$

where ${\displaystyle A}$, ${\displaystyle B}$, and ${\displaystyle C}$ are the angles at the three vertices.

The Cartesian coordinates of the incenter are a weighted average of the coordinates of the three vertices using the side lengths of the triangle relative to the perimeter (that is, using the barycentric coordinates given above, normalized to sum to unity) as weights. The weights are positive so the incenter lies inside the triangle as stated above. If the three vertices are located at ${\displaystyle (x_{a},y_{a})}$, ${\displaystyle (x_{b},y_{b})}$, and ${\displaystyle (x_{c},y_{c})}$, and the sides opposite these vertices have corresponding lengths ${\displaystyle a}$, ${\displaystyle b}$, and ${\displaystyle c}$, then the incenter is at^{[citation needed]}

$${\displaystyle \left({\frac {ax_{a}+bx_{b}+cx_{c}}{a+b+c}},{\frac {ay_{a}+by_{b}+cy_{c}}{a+b+c}}\right)={\frac {a\left(x_{a},y_{a}\right)+b\left(x_{b},y_{b}\right)+c\left(x_{c},y_{c}\right)}{a+b+c}}.}$$

The inradius ${\displaystyle r}$ of the incircle in a triangle with sides of length ${\displaystyle a}$, ${\displaystyle b}$, ${\displaystyle c}$ is given by^[7]

$${\displaystyle r={\sqrt {\frac {(s-a)(s-b)(s-c)}{s}}},}$$

where ${\displaystyle s={\tfrac {1}{2}}(a+b+c)}$ is the semiperimeter (see Heron's formula).

The tangency points of the incircle divide the sides into segments of lengths ${\displaystyle s-a}$ from ${\displaystyle A}$, ${\displaystyle s-b}$ from ${\displaystyle B}$, and ${\displaystyle s-c}$ from ${\displaystyle C}$ (see Tangent lines to a circle).^[8]

Denote the incenter of ${\displaystyle \triangle ABC}$ as ${\displaystyle I}$.

The distance from vertex ${\displaystyle A}$ to the incenter ${\displaystyle I}$ is:

$${\displaystyle {\overline {AI}}=d(A,I)=c\,{\frac {\sin {\frac {B}{2}}}{\cos {\frac {C}{2}}}}=b\,{\frac {\sin {\frac {C}{2}}}{\cos {\frac {B}{2}}}}.}$$

Use the Law of sines in the triangle ${\displaystyle \triangle IAB}$.

We get ${\displaystyle {\frac {\overline {AI}}{\sin {\frac {B}{2}}}}={\frac {c}{\sin \angle AIB}}}$. We have that ${\displaystyle \angle AIB=\pi -{\frac {A}{2}}-{\frac {B}{2}}={\frac {\pi }{2}}+{\frac {C}{2}}}$.

It follows that ${\displaystyle {\overline {AI}}=c\ {\frac {\sin {\frac {B}{2}}}{\cos {\frac {C}{2}}}}}$.

The equality with the second expression is obtained the same way.

The distances from the incenter to the vertices combined with the lengths of the triangle sides obey the equation^[9]

$${\displaystyle {\frac {{\overline {IA}}\cdot {\overline {IA}}}{{\overline {CA}}\cdot {\overline {AB}}}}+{\frac {{\overline {IB}}\cdot {\overline {IB}}}{{\overline {AB}}\cdot {\overline {BC}}}}+{\frac {{\overline {IC}}\cdot {\overline {IC}}}{{\overline {BC}}\cdot {\overline {CA}}}}=1.}$$

Additionally,^[10]

$${\displaystyle {\overline {IA}}\cdot {\overline {IB}}\cdot {\overline {IC}}=4Rr^{2},}$$

where ${\displaystyle R}$ and ${\displaystyle r}$ are the triangle's circumradius and inradius respectively.

The collection of triangle centers may be given the structure of a group under coordinate-wise multiplication of trilinear coordinates; in this group, the incenter forms the identity element.^[6]

The distances from a vertex to the two nearest touchpoints are equal; for example:^[11]

$${\displaystyle d\left(A,T_{B}\right)=d\left(A,T_{C}\right)={\tfrac {1}{2}}(b+c-a)=s-a.}$$

If the altitudes from sides of lengths ${\displaystyle a}$, ${\displaystyle b}$, and ${\displaystyle c}$ are ${\displaystyle h_{a}}$, ${\displaystyle h_{b}}$, and ${\displaystyle h_{c}}$, then the inradius ${\displaystyle r}$ is one third the harmonic mean of these altitudes; that is,^[12]

$${\displaystyle r={\frac {1}{{\dfrac {1}{h_{a}}}+{\dfrac {1}{h_{b}}}+{\dfrac {1}{h_{c}}}}}.}$$

The product of the incircle radius ${\displaystyle r}$ and the circumcircle radius ${\displaystyle R}$ of a triangle with sides ${\displaystyle a}$, ${\displaystyle b}$, and ${\displaystyle c}$ is^[13]

$${\displaystyle rR={\frac {abc}{2(a+b+c)}}.}$$

Some relations among the sides, incircle radius, and circumcircle radius are:^[14]

$${\displaystyle {\begin{aligned}ab+bc+ca&=s^{2}+(4R+r)r,\\a^{2}+b^{2}+c^{2}&=2s^{2}-2(4R+r)r.\end{aligned}}}$$

Any line through a triangle that splits both the triangle's area and its perimeter in half goes through the triangle's incenter (the center of its incircle). There are either one, two, or three of these for any given triangle.^[15]

The incircle radius is no greater than one-ninth the sum of the altitudes.^[16]: 289

The squared distance from the incenter ${\displaystyle I}$ to the circumcenter ${\displaystyle O}$ is given by^[17]: 232

$${\displaystyle {\overline {OI}}^{2}=R(R-2r)={\frac {a\,b\,c\,}{a+b+c}}\left[{\frac {a\,b\,c\,}{(a+b-c)\,(a-b+c)\,(-a+b+c)}}-1\right]}$$

and the distance from the incenter to the center ${\displaystyle N}$ of the nine point circle is^[17]: 232

$${\displaystyle {\overline {IN}}={\tfrac {1}{2}}(R-2r)<{\tfrac {1}{2}}R.}$$

The incenter lies in the medial triangle (whose vertices are the midpoints of the sides).^{[17]: 233, Lemma 1}

The radius of the incircle is related to the area of the triangle.^[18] The ratio of the area of the incircle to the area of the triangle is less than or equal to ${\displaystyle \pi {\big /}3{\sqrt {3}}}$, with equality holding only for equilateral triangles.^[19]

Suppose ${\displaystyle \triangle ABC}$ has an incircle with radius ${\displaystyle r}$ and center ${\displaystyle I}$. Let ${\displaystyle a}$ be the length of ${\displaystyle {\overline {BC}}}$, ${\displaystyle b}$ the length of ${\displaystyle {\overline {AC}}}$, and ${\displaystyle c}$ the length of ${\displaystyle {\overline {AB}}}$.

Now, the incircle is tangent to ${\displaystyle {\overline {AB}}}$ at some point ${\displaystyle T_{C}}$, and so ${\displaystyle \angle AT_{C}I}$ is right. Thus, the radius ${\displaystyle T_{C}I}$ is an altitude of ${\displaystyle \triangle IAB}$.

Therefore, ${\displaystyle \triangle IAB}$ has base length ${\displaystyle c}$ and height ${\displaystyle r}$, and so has area ${\displaystyle {\tfrac {1}{2}}cr}$.

Similarly, ${\displaystyle \triangle IAC}$ has area ${\displaystyle {\tfrac {1}{2}}br}$ and ${\displaystyle \triangle IBC}$ has area ${\displaystyle {\tfrac {1}{2}}ar}$.

Since these three triangles decompose ${\displaystyle \triangle ABC}$, we see that the area ${\displaystyle \Delta {\text{ of}}\triangle ABC}$ is:

$${\displaystyle \Delta ={\tfrac {1}{2}}(a+b+c)r=sr,}$$

     and     ${\displaystyle r={\frac {\Delta }{s}},}$

where ${\displaystyle \Delta }$ is the area of ${\displaystyle \triangle ABC}$ and ${\displaystyle s={\tfrac {1}{2}}(a+b+c)}$ is its semiperimeter.

For an alternative formula, consider ${\displaystyle \triangle IT_{C}A}$. This is a right-angled triangle with one side equal to ${\displaystyle r}$ and the other side equal to ${\displaystyle r\cot {\tfrac {A}{2}}}$. The same is true for ${\displaystyle \triangle IB'A}$. The large triangle is composed of six such triangles and the total area is:^{[citation needed]}

$${\displaystyle \Delta =r^{2}\left(\cot {\tfrac {A}{2}}+\cot {\tfrac {B}{2}}+\cot {\tfrac {C}{2}}\right).}$$

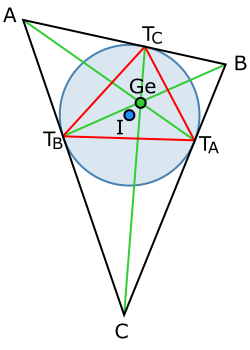
The Gergonne triangle (of ${\displaystyle \triangle ABC}$) is defined by the three touchpoints of the incircle on the three sides. The touchpoint opposite ${\displaystyle A}$ is denoted ${\displaystyle T_{A}}$, etc.

This Gergonne triangle, ${\displaystyle \triangle T_{A}T_{B}T_{C}}$, is also known as the contact triangle or intouch triangle of ${\displaystyle \triangle ABC}$. Its area is

$${\displaystyle K_{T}=K{\frac {2r^{2}s}{abc}}}$$

where ${\displaystyle K}$, ${\displaystyle r}$, and ${\displaystyle s}$ are the area, radius of the incircle, and semiperimeter of the original triangle, and ${\displaystyle a}$, ${\displaystyle b}$, and ${\displaystyle c}$ are the side lengths of the original triangle. This is the same area as that of the extouch triangle.^[20]

The three lines ${\displaystyle AT_{A}}$, ${\displaystyle BT_{B}}$, and ${\displaystyle CT_{C}}$ intersect in a single point called the Gergonne point, denoted as ${\displaystyle G_{e}}$ (or triangle center X₇). The Gergonne point lies in the open orthocentroidal disk punctured at its own center, and can be any point therein.^[21]

The Gergonne point of a triangle has a number of properties, including that it is the symmedian point of the Gergonne triangle.^[22]

Trilinear coordinates for the vertices of the intouch triangle are given by^{[citation needed]}

$${\displaystyle {\begin{array}{ccccccc}T_{A}&=&0&:&\sec ^{2}{\frac {B}{2}}&:&\sec ^{2}{\frac {C}{2}}\\[2pt]T_{B}&=&\sec ^{2}{\frac {A}{2}}&:&0&:&\sec ^{2}{\frac {C}{2}}\\[2pt]T_{C}&=&\sec ^{2}{\frac {A}{2}}&:&\sec ^{2}{\frac {B}{2}}&:&0.\end{array}}}$$

Trilinear coordinates for the Gergonne point are given by^{[citation needed]}

$${\displaystyle \sec ^{2}{\tfrac {A}{2}}:\sec ^{2}{\tfrac {B}{2}}:\sec ^{2}{\tfrac {C}{2}},}$$

or, equivalently, by the Law of Sines,

$${\displaystyle {\frac {bc}{b+c-a}}:{\frac {ca}{c+a-b}}:{\frac {ab}{a+b-c}}.}$$

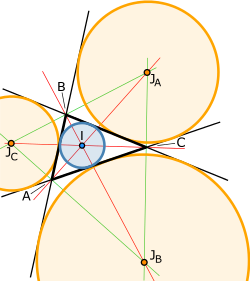
An excircle or escribed circle^[2] of the triangle is a circle lying outside the triangle, tangent to one of its sides, and tangent to the extensions of the other two. Every triangle has three distinct excircles, each tangent to one of the triangle's sides.^[3]

The center of an excircle is the intersection of the internal bisector of one angle (at vertex ${\displaystyle A}$, for example) and the external bisectors of the other two. The center of this excircle is called the excenter relative to the vertex ${\displaystyle A}$, or the excenter of ${\displaystyle A}$.^[3] Because the internal bisector of an angle is perpendicular to its external bisector, it follows that the center of the incircle together with the three excircle centers form an orthocentric system.^[5]

While the incenter of ${\displaystyle \triangle ABC}$ has trilinear coordinates ${\displaystyle 1:1:1}$, the excenters have trilinears^{[citation needed]}

$${\displaystyle {\begin{array}{rrcrcr}J_{A}=&-1&:&1&:&1\\J_{B}=&1&:&-1&:&1\\J_{C}=&1&:&1&:&-1\end{array}}}$$

The radii of the excircles are called the exradii.

The exradius of the excircle opposite ${\displaystyle A}$ (so touching ${\displaystyle BC}$, centered at ${\displaystyle J_{A}}$) is^[23][24]

$${\displaystyle r_{a}={\frac {rs}{s-a}}={\sqrt {\frac {s(s-b)(s-c)}{s-a}}},}$$ where ${\displaystyle s={\tfrac {1}{2}}(a+b+c).}$

See Heron's formula.

Source:^[23]

Let the excircle at side ${\displaystyle AB}$ touch at side ${\displaystyle AC}$ extended at ${\displaystyle G}$, and let this excircle's radius be ${\displaystyle r_{c}}$ and its center be ${\displaystyle J_{c}}$. Then ${\displaystyle J_{c}G}$ is an altitude of ${\displaystyle \triangle ACJ_{c}}$, so ${\displaystyle \triangle ACJ_{c}}$ has area ${\displaystyle {\tfrac {1}{2}}br_{c}}$. By a similar argument, ${\displaystyle \triangle BCJ_{c}}$ has area ${\displaystyle {\tfrac {1}{2}}ar_{c}}$ and ${\displaystyle \triangle ABJ_{c}}$ has area ${\displaystyle {\tfrac {1}{2}}cr_{c}}$. Thus the area ${\displaystyle \Delta }$ of triangle ${\displaystyle \triangle ABC}$ is

$${\displaystyle \Delta ={\tfrac {1}{2}}(a+b-c)r_{c}=(s-c)r_{c}}$$.

So, by symmetry, denoting ${\displaystyle r}$ as the radius of the incircle,

$${\displaystyle \Delta =sr=(s-a)r_{a}=(s-b)r_{b}=(s-c)r_{c}}$$.

By the Law of Cosines, we have

$${\displaystyle \cos A={\frac {b^{2}+c^{2}-a^{2}}{2bc}}}$$

Combining this with the identity ${\displaystyle \sin ^{2}\!A+\cos ^{2}\!A=1}$, we have

$${\displaystyle \sin A={\frac {\sqrt {-a^{4}-b^{4}-c^{4}+2a^{2}b^{2}+2b^{2}c^{2}+2a^{2}c^{2}}}{2bc}}}$$

But ${\displaystyle \Delta ={\tfrac {1}{2}}bc\sin A}$, and so

$${\displaystyle {\begin{aligned}\Delta &={\tfrac {1}{4}}{\sqrt {-a^{4}-b^{4}-c^{4}+2a^{2}b^{2}+2b^{2}c^{2}+2a^{2}c^{2}}}\\[5mu]&={\tfrac {1}{4}}{\sqrt {(a+b+c)(-a+b+c)(a-b+c)(a+b-c)}}\\[5mu]&={\sqrt {s(s-a)(s-b)(s-c)}},\end{aligned}}}$$

which is Heron's formula.

Combining this with ${\displaystyle sr=\Delta }$, we have

$${\displaystyle r^{2}={\frac {\Delta ^{2}}{s^{2}}}={\frac {(s-a)(s-b)(s-c)}{s}}.}$$

Similarly, ${\displaystyle (s-a)r_{a}=\Delta }$ gives

$${\displaystyle {\begin{aligned}&r_{a}^{2}={\frac {s(s-b)(s-c)}{s-a}}\\[4pt]&\implies r_{a}={\sqrt {\frac {s(s-b)(s-c)}{s-a}}}.\end{aligned}}}$$

From the formulas above one can see that the excircles are always larger than the incircle and that the largest excircle is the one tangent to the longest side and the smallest excircle is tangent to the shortest side. Further, combining these formulas yields:^[25]

$${\displaystyle \Delta ={\sqrt {rr_{a}r_{b}r_{c}}}.}$$

The circular hull of the excircles is internally tangent to each of the excircles and is thus an Apollonius circle.^[26] The radius of this Apollonius circle is ${\displaystyle {\tfrac {r^{2}+s^{2}}{4r}}}$ where ${\displaystyle r}$ is the incircle radius and ${\displaystyle s}$ is the semiperimeter of the triangle.^[27]

The following relations hold among the inradius ${\displaystyle r}$, the circumradius ${\displaystyle R}$, the semiperimeter ${\displaystyle s}$, and the excircle radii ${\displaystyle r_{a}}$, ${\displaystyle r_{b}}$, ${\displaystyle r_{c}}$:^[14]

$${\displaystyle {\begin{aligned}r_{a}+r_{b}+r_{c}&=4R+r,\\r_{a}r_{b}+r_{b}r_{c}+r_{c}r_{a}&=s^{2},\\r_{a}^{2}+r_{b}^{2}+r_{c}^{2}&=\left(4R+r\right)^{2}-2s^{2}.\end{aligned}}}$$

The circle through the centers of the three excircles has radius ${\displaystyle 2R}$.^[14]

If ${\displaystyle H}$ is the orthocenter of ${\displaystyle \triangle ABC}$, then^[14]

$${\displaystyle {\begin{aligned}r_{a}+r_{b}+r_{c}+r&={\overline {AH}}+{\overline {BH}}+{\overline {CH}}+2R,\\r_{a}^{2}+r_{b}^{2}+r_{c}^{2}+r^{2}&={\overline {AH}}^{2}+{\overline {BH}}^{2}+{\overline {CH}}^{2}+(2R)^{2}.\end{aligned}}}$$

The Nagel triangle or extouch triangle of ${\displaystyle \triangle ABC}$ is denoted by the vertices ${\displaystyle T_{A}}$, ${\displaystyle T_{B}}$, and ${\displaystyle T_{C}}$ that are the three points where the excircles touch the reference ${\displaystyle \triangle ABC}$ and where ${\displaystyle T_{A}}$ is opposite of ${\displaystyle A}$, etc. This ${\displaystyle \triangle T_{A}T_{B}T_{C}}$ is also known as the extouch triangle of ${\displaystyle \triangle ABC}$. The circumcircle of the extouch ${\displaystyle \triangle T_{A}T_{B}T_{C}}$ is called the Mandart circle (cf. Mandart inellipse).

The three line segments ${\displaystyle {\overline {AT_{A}}}}$, ${\displaystyle {\overline {BT_{B}}}}$ and ${\displaystyle {\overline {CT_{C}}}}$ are called the splitters of the triangle; they each bisect the perimeter of the triangle,^{[citation needed]}

$${\displaystyle {\overline {AB}}+{\overline {BT_{A}}}={\overline {AC}}+{\overline {CT_{A}}}={\frac {1}{2}}\left({\overline {AB}}+{\overline {BC}}+{\overline {AC}}\right).}$$

The splitters intersect in a single point, the triangle's Nagel point ${\displaystyle N_{a}}$ (or triangle center X₈).

Trilinear coordinates for the vertices of the extouch triangle are given by^{[citation needed]}

$${\displaystyle {\begin{array}{ccccccc}T_{A}&=&0&:&\csc ^{2}{\frac {B}{2}}&:&\csc ^{2}{\frac {C}{2}}\\[2pt]T_{B}&=&\csc ^{2}{\frac {A}{2}}&:&0&:&\csc ^{2}{\frac {C}{2}}\\[2pt]T_{C}&=&\csc ^{2}{\frac {A}{2}}&:&\csc ^{2}{\frac {B}{2}}&:&0\end{array}}}$$

Trilinear coordinates for the Nagel point are given by^{[citation needed]}

$${\displaystyle \csc ^{2}{\tfrac {A}{2}}:\csc ^{2}{\tfrac {B}{2}}:\csc ^{2}{\tfrac {C}{2}},}$$

or, equivalently, by the Law of Sines,

$${\displaystyle {\frac {b+c-a}{a}}:{\frac {c+a-b}{b}}:{\frac {a+b-c}{c}}.}$$

The Nagel point is the isotomic conjugate of the Gergonne point.^{[citation needed]}

In geometry, the nine-point circle is a circle that can be constructed for any given triangle. It is so named because it passes through nine significant concyclic points defined from the triangle. These nine points are:^[28][29]

• The midpoint of each side of the triangle
• The foot of each altitude
• The midpoint of the line segment from each vertex of the triangle to the orthocenter (where the three altitudes meet; these line segments lie on their respective altitudes).

In 1822, Karl Feuerbach discovered that any triangle's nine-point circle is externally tangent to that triangle's three excircles and internally tangent to its incircle; this result is known as Feuerbach's theorem. He proved that:^[30]

... the circle which passes through the feet of the altitudes of a triangle is tangent to all four circles which in turn are tangent to the three sides of the triangle ... (Feuerbach 1822)

The triangle center at which the incircle and the nine-point circle touch is called the Feuerbach point.

The incircle may be described as the pedal circle of the incenter. The locus of points whose pedal circles are tangent to the nine-point circle is known as the McCay cubic.

The points of intersection of the interior angle bisectors of ${\displaystyle \triangle ABC}$ with the segments ${\displaystyle BC}$, ${\displaystyle CA}$, and ${\displaystyle AB}$ are the vertices of the incentral triangle. Trilinear coordinates for the vertices of the incentral triangle ${\displaystyle \triangle A'B'C'}$ are given by^{[citation needed]}

$${\displaystyle {\begin{array}{ccccccc}A'&=&0&:&1&:&1\\[2pt]B'&=&1&:&0&:&1\\[2pt]C'&=&1&:&1&:&0\end{array}}}$$

The excentral triangle of a reference triangle has vertices at the centers of the reference triangle's excircles. Its sides are on the external angle bisectors of the reference triangle (see figure at top of page). Trilinear coordinates for the vertices of the excentral triangle ${\displaystyle \triangle A'B'C'}$ are given by^{[citation needed]}

$${\displaystyle {\begin{array}{ccrcrcr}A'&=&-1&:&1&:&1\\[2pt]B'&=&1&:&-1&:&1\\[2pt]C'&=&1&:&1&:&-1\end{array}}}$$

Let ${\displaystyle x:y:z}$ be a variable point in trilinear coordinates, and let ${\displaystyle u=\cos ^{2}\left(A/2\right)}$, ${\displaystyle v=\cos ^{2}\left(B/2\right)}$, ${\displaystyle w=\cos ^{2}\left(C/2\right)}$. The four circles described above are given equivalently by either of the two given equations:^{[31]: 210–215}

• Incircle:$${\displaystyle {\begin{aligned}u^{2}x^{2}+v^{2}y^{2}+w^{2}z^{2}-2vwyz-2wuzx-2uvxy&=0\\[4pt]{\textstyle \pm {\sqrt {x}}\cos {\tfrac {A}{2}}\pm {\sqrt {y{\vphantom {t}}}}\cos {\tfrac {B}{2}}\pm {\sqrt {z}}\cos {\tfrac {C}{2}}}&=0\end{aligned}}}$$
• ${\displaystyle A}$-excircle:$${\displaystyle {\begin{aligned}u^{2}x^{2}+v^{2}y^{2}+w^{2}z^{2}-2vwyz+2wuzx+2uvxy&=0\\[4pt]{\textstyle \pm {\sqrt {-x}}\cos {\tfrac {A}{2}}\pm {\sqrt {y{\vphantom {t}}}}\cos {\tfrac {B}{2}}\pm {\sqrt {z}}\cos {\tfrac {C}{2}}}&=0\end{aligned}}}$$
• ${\displaystyle B}$-excircle:$${\displaystyle {\begin{aligned}u^{2}x^{2}+v^{2}y^{2}+w^{2}z^{2}+2vwyz-2wuzx+2uvxy&=0\\[4pt]{\textstyle \pm {\sqrt {x}}\cos {\tfrac {A}{2}}\pm {\sqrt {-y{\vphantom {t}}}}\cos {\tfrac {B}{2}}\pm {\sqrt {z}}\cos {\tfrac {C}{2}}}&=0\end{aligned}}}$$
• ${\displaystyle C}$-excircle:$${\displaystyle {\begin{aligned}u^{2}x^{2}+v^{2}y^{2}+w^{2}z^{2}+2vwyz+2wuzx-2uvxy&=0\\[4pt]{\textstyle \pm {\sqrt {x}}\cos {\tfrac {A}{2}}\pm {\sqrt {y{\vphantom {t}}}}\cos {\tfrac {B}{2}}\pm {\sqrt {-z}}\cos {\tfrac {C}{2}}}&=0\end{aligned}}}$$

Euler's theorem states that in a triangle:

$${\displaystyle (R-r)^{2}=d^{2}+r^{2},}$$

where ${\displaystyle R}$ and ${\displaystyle r}$ are the circumradius and inradius respectively, and ${\displaystyle d}$ is the distance between the circumcenter and the incenter.

For excircles the equation is similar:

$${\displaystyle \left(R+r_{\text{ex}}\right)^{2}=d_{\text{ex}}^{2}+r_{\text{ex}}^{2},}$$

where ${\displaystyle r_{\text{ex}}}$ is the radius of one of the excircles, and ${\displaystyle d_{\text{ex}}}$ is the distance between the circumcenter and that excircle's center.^[32][33][34]

Some (but not all) quadrilaterals have an incircle. These are called tangential quadrilaterals. Among their many properties perhaps the most important is that their two pairs of opposite sides have equal sums. This is called the Pitot theorem.^[35]

More generally, a polygon with any number of sides that has an inscribed circle (that is, one that is tangent to each side) is called a tangential polygon.

If you consider topological triangles, you can also define a notion of inscribed circle that fits inside. It is no longer described as tangent to all sides since your topological triangle might not be differentiable everywhere. Rather it is defined as a circle whose center has the same minimal distance to each side. Its a proven fact that an inscribed circle always exists in any topological triangle^[36].

• Circumcenter – Circle that passes through the vertices of a trianglePages displaying short descriptions of redirect targets
• Circumcircle – Circle that passes through the vertices of a triangle
• Circumconic and inconic – Conic section that passes through the vertices of a triangle or is tangent to its sides
• Circumgon – Geometric figure which circumscribes a circle
• Ex-tangential quadrilateral – Convex 4-sided polygon whose sidelines are all tangent to an outside circle
• Harcourt's theorem – Area of a triangle from its sides and vertex distances to any line tangent to its incircle
• Incenter–excenter lemma – Theorem about inscribed and circumscribed circles
• Inscribed sphere – Sphere tangent to every face of a polyhedron
• Power of a point – Relative distance of a point from a circle
• Steiner inellipse – Unique ellipse tangent to all 3 midpoints of a given triangle's sides
• Tangential quadrilateral – Polygon whose four sides all touch a circle
• Triangle conic