Index notation

It is frequently helpful in mathematics to refer to the elements of an array using subscripts. The subscripts can be integers or variables. The array takes the form of tensors in general, since these can be treated as multi-dimensional arrays. Special (and more familiar) cases are vectors (1d arrays) and matrices (2d arrays).

The following is only an introduction to the concept: index notation is used in more detail in mathematics (particularly in the representation and manipulation of tensor operations). See the main article for further details.

A vector treated as an array of numbers by writing as a row vector or column vector (whichever is used depends on convenience or context):

${\displaystyle \mathbf {a} ={\begin{pmatrix}a_{1}\\a_{2}\\\vdots \\a_{n}\end{pmatrix}},\quad \mathbf {a} ={\begin{pmatrix}a_{1}&a_{2}&\cdots &a_{n}\end{pmatrix}}}$

Index notation allows indication of the elements of the array by simply writing a_i, where the index i is known to run from 1 to n, because of n-dimensions.^[1] For example, given the vector:

${\displaystyle \mathbf {a} ={\begin{pmatrix}10&8&9&6&3&5\\\end{pmatrix}}}$

then some entries are

${\displaystyle a_{1}=10,\,a_{2}=8,\,\cdots ,\,a_{6}=5}$.

The notation can be applied to vectors in mathematics and physics. The following vector equation

${\displaystyle \mathbf {a} +\mathbf {b} =\mathbf {c} }$

can also be written in terms of the elements of the vector (aka components), that is

${\displaystyle a_{i}+b_{i}=c_{i}}$

where the indices take a given range of values. This expression represents a set of equations, one for each index. If the vectors each have n elements, meaning i = 1,2,…n, then the equations are explicitly

${\displaystyle {\begin{aligned}a_{1}+b_{1}&=c_{1}\\a_{2}+b_{2}&=c_{2}\\&\ \ \vdots \\a_{n}+b_{n}&=c_{n}\end{aligned}}}$

Hence, index notation serves as an efficient shorthand for

1. representing the general structure to an equation,
2. while applicable to individual components.

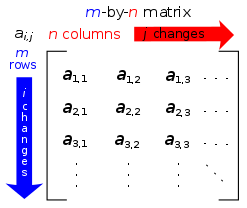
More than one index is used to describe arrays of numbers, in two or more dimensions, such as the elements of a matrix, (see also image to right);

${\displaystyle \mathbf {A} ={\begin{pmatrix}a_{11}&a_{12}&\cdots &a_{1n}\\a_{21}&a_{22}&\cdots &a_{2n}\\\vdots &\vdots &\ddots &\vdots \\a_{m1}&a_{m2}&\cdots &a_{mn}\\\end{pmatrix}}}$

The entry of a matrix A is written using two indices, say i and j, with or without commas to separate the indices: a_ij or a_i,j, where the first subscript is the row number and the second is the column number. Juxtaposition is also used as notation for multiplication; this may be a source of confusion. For example, if

${\displaystyle \mathbf {A} ={\begin{pmatrix}9&8&6\\1&2&7\\4&9&2\\6&0&5\end{pmatrix}}}$

then some entries are

${\displaystyle a_{11}=9,\,a_{12}=8,\,a_{21}=1,\,\cdots ,\,a_{23}=7,\,\cdots }$.

For indices larger than 9, the comma-based notation may be preferable (e.g., a_3,12 instead of a₃₁₂).

Matrix equations are written similarly to vector equations, such as

${\displaystyle \mathbf {A} +\mathbf {B} =\mathbf {C} }$

in terms of the elements of the matrices (aka components)

${\displaystyle A_{ij}+B_{ij}=C_{ij}}$

for all values of i and j. Again this expression represents a set of equations, one for each index. If the matrices each have m rows and n columns, meaning i = 1, 2, …, m and j = 1, 2, …, n, then there are mn equations.

The notation allows a clear generalization to multi-dimensional arrays of elements: tensors. For example,

${\displaystyle A_{i_{1}i_{2}\cdots }+B_{i_{1}i_{2}\cdots }=C_{i_{1}i_{2}\cdots }}$

representing a set of many equations.

In tensor analysis, superscripts are used instead of subscripts to distinguish covariant from contravariant entities, see covariance and contravariance of vectors and raising and lowering indices.

In several programming languages, index notation is a way of addressing elements of an array. This method is used since it is closest to how it is implemented in assembly language whereby the address of the first element is used as a base, and a multiple (the index) of the element size is used to address inside the array.

For example, if an array of integers is stored in a region of the computer's memory starting at the memory cell with address 3000 (the base address), and each integer occupies four cells (bytes), then the elements of this array are at memory locations 0x3000, 0x3004, 0x3008, …, 0x3000 + 4(n − 1) (note the zero-based numbering). In general, the address of the ith element of an array with base address b and element size s is b + is.

In the C programming language, we can write the above as *(base + i) (pointer form) or base[i] (array indexing form), which is exactly equivalent because the C standard defines the array indexing form as a transformation to pointer form. Coincidentally, since pointer addition is commutative, this allows for obscure expressions such as 3[base] which is equivalent to base[3].^[2]

Things become more interesting when we consider arrays with more than one index, for example, a two-dimensional table. We have three possibilities:

• make the two-dimensional array one-dimensional by computing a single index from the two
• consider a one-dimensional array where each element is another one-dimensional array, i.e. an array of arrays
• use additional storage to hold the array of addresses of each row of the original array, and store the rows of the original array as separate one-dimensional arrays

In C, all three methods can be used. When the first method is used, the programmer decides how the elements of the array are laid out in the computer's memory, and provides the formulas to compute the location of each element. The second method is used when the number of elements in each row is the same and known at the time the program is written. The programmer declares the array to have, say, three columns by writing e.g. elementtype tablename[][3];. One then refers to a particular element of the array by writing tablename[first index][second index]. The compiler computes the total number of memory cells occupied by each row, uses the first index to find the address of the desired row, and then uses the second index to find the address of the desired element in the row. When the third method is used, the programmer declares the table to be an array of pointers, like in elementtype *tablename[];. When the programmer subsequently specifies a particular element tablename[first index][second index], the compiler generates instructions to look up the address of the row specified by the first index, and use this address as the base when computing the address of the element specified by the second index.

void mult3x3f(float result[][3], const float A[][3], const float B[][3])
{
  int i, j, k;
  for (i = 0; i < 3; ++i) {
    for (j = 0; j < 3; ++j) {
      result[i][j] = 0;
      for (k = 0; k < 3; ++k)
        result[i][j] += A[i][k] * B[k][j];
    }
  }
}

In other programming languages such as Pascal, indices may start at 1, so indexing in a block of memory can be changed to fit a start-at-1 addressing scheme by a simple linear transformation – in this scheme, the memory location of the ith element with base address b and element size s is b + (i − 1)s.