Recent from talks
Nothing was collected or created yet.
Splay tree
View on Wikipedia
| Splay tree | |||||||||||||||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Type | Tree | ||||||||||||||||||||||||||||
| Invented | 1985 | ||||||||||||||||||||||||||||
| Invented by | Daniel Dominic Sleator and Robert Endre Tarjan | ||||||||||||||||||||||||||||
| Complexities in big O notation | |||||||||||||||||||||||||||||
| |||||||||||||||||||||||||||||
A splay tree is a binary search tree with the additional property that recently accessed elements are quick to access again. Like self-balancing binary search trees, a splay tree performs basic operations such as insertion, look-up and removal in O(log n) amortized time. For random access patterns drawn from a non-uniform random distribution, their amortized time can be faster than logarithmic, proportional to the entropy of the access pattern. For many patterns of non-random operations, also, splay trees can take better than logarithmic time, without requiring advance knowledge of the pattern. According to the unproven dynamic optimality conjecture, their performance on all access patterns is within a constant factor of the best possible performance that could be achieved by any other self-adjusting binary search tree, even one selected to fit that pattern. The splay tree was invented by Daniel Sleator and Robert Tarjan in 1985.[1]
All normal operations on a binary search tree are combined with one basic operation, called splaying. Splaying the tree for a certain element rearranges the tree so that the element is placed at the root of the tree. One way to do this with the basic search operation is to first perform a standard binary tree search for the element in question, and then use tree rotations in a specific fashion to bring the element to the top. Alternatively, a top-down algorithm can combine the search and the tree reorganization into a single phase.
Advantages
[edit]Good performance for a splay tree depends on the fact that it is self-optimizing, in that frequently accessed nodes will move nearer to the root where they can be accessed more quickly. The worst-case height—though unlikely—is O(n), with the average being O(log n). Having frequently-used nodes near the root is an advantage for many practical applications (also see locality of reference), and is particularly useful for implementing caches and garbage collection algorithms.
Advantages include:
- Comparable performance: Average-case performance is as efficient as other trees.[3]
- Small memory footprint: Splay trees do not need to store any bookkeeping data.
Disadvantages
[edit]The most significant disadvantage of splay trees is that the height of a splay tree can be linear.[2]: 1 For example, this will be the case after accessing all n elements in non-decreasing order. Since the height of a tree corresponds to the worst-case access time, this means that the actual cost of a single operation can be high. However the amortized access cost of this worst case is logarithmic, O(log n). Also, the expected access cost can be reduced to O(log n) by using a randomized variant.[4]
The representation of splay trees can change even when they are accessed in a 'read-only' manner (i.e. by find operations). This complicates the use of such splay trees in a multi-threaded environment. Specifically, extra management is needed if multiple threads are allowed to perform find operations concurrently. This also makes them unsuitable for general use in purely functional programming, although even there they can be used in limited ways to implement priority queues.
Finally, when the access pattern is random, the additional splaying overhead adds a significant constant factor to the cost compared to less-dynamic alternatives.
Operations
[edit]Splaying
[edit]When a node x is accessed, a splay operation is performed on x to move it to the root. A splay operation is a sequence of splay steps, each of which moves x closer to the root. By performing a splay operation on the node of interest after every access, the recently accessed nodes are kept near the root and the tree remains roughly balanced, so it provides the desired amortized time bounds.
Each particular step depends on three factors:
- Whether x is the left or right child of its parent node, p,
- whether p is the root or not, and if not
- whether p is the left or right child of its parent, g (the grandparent of x).
There are three types of splay steps, each of which has two symmetric variants: left- and right-handed. For the sake of brevity, only one of these two is shown for each type. (In the following diagrams, circles indicate nodes of interest and triangles indicate sub-trees of arbitrary size.) The three types of splay steps are:
Zig step: this step is done when p is the root. The tree is rotated on the edge between x and p. Zig steps exist to deal with the parity issue, will be done only as the last step in a splay operation, and only when x has odd depth at the beginning of the operation.

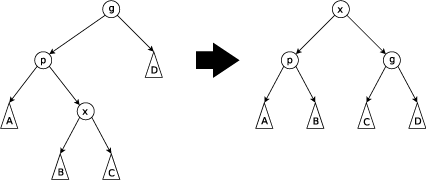
Zig-zig step: this step is done when p is not the root and x and p are either both right children or are both left children. The picture below shows the case where x and p are both left children. The tree is rotated on the edge joining p with its parent g, then rotated on the edge joining x with p. Zig-zig steps are the only thing that differentiate splay trees from the rotate to root method introduced by Allen and Munro[5] prior to the introduction of splay trees.
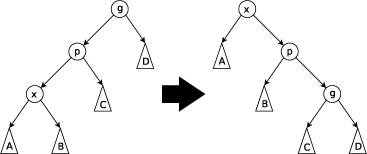
Zig-zag step: this step is done when p is not the root and x is a right child and p is a left child or vice versa (x is left, p is right). The tree is rotated on the edge between p and x, and then rotated on the resulting edge between x and g.
Join
[edit]Given two trees S and T such that all elements of S are smaller than the elements of T, the following steps can be used to join them to a single tree:
- Splay the largest item in S. Now this item is in the root of S and has a null right child.
- Set the right child of the new root to T.
Split
[edit]Given a tree and an element x, return two new trees: one containing all elements less than or equal to x and the other containing all elements greater than x. This can be done in the following way:
- Splay x. Now it is in the root so the tree to its left contains all elements smaller than x and the tree to its right contains all element larger than x.
- Split the right subtree from the rest of the tree.
Insertion
[edit]To insert a value x into a splay tree:
- Insert x as with a normal binary search tree.
- Perform a splay on x.
As a result, the newly inserted node x becomes the root of the tree.
Alternatively:
- Use the split operation to split the tree at the value of x to two sub-trees: S and T.
- Create a new tree in which x is the root, S is its left sub-tree and T its right sub-tree.
Deletion
[edit]To delete a node x, use the same method as with a binary search tree:
- If x has two children:
- Swap its value with that of either the rightmost node of its left sub tree (its in-order predecessor) or the leftmost node of its right subtree (its in-order successor).
- Remove that node instead.
In this way, deletion is reduced to the problem of removing a node with 0 or 1 children. Unlike a binary search tree, in a splay tree after deletion, we splay the parent of the removed node to the top of the tree.
Alternatively:
- The node to be deleted is first splayed, i.e. brought to the root of the tree and then deleted. leaves the tree with two sub trees.
- The two sub-trees are then joined using a "join" operation.
Implementation and variants
[edit]Splaying, as mentioned above, is performed during a second, bottom-up pass over the access path of a node. It is possible to record the access path during the first pass for use during the second, but that requires extra space during the access operation. Another alternative is to keep a parent pointer in every node, which avoids the need for extra space during access operations but may reduce overall time efficiency because of the need to update those pointers.[1]
Another method which can be used is based on the argument that the tree can be restructured during the way down the access path instead of making a second pass. This top-down splaying routine uses three sets of nodes – left tree, right tree and middle tree. The first two contain all items of original tree known to be less than or greater than current item respectively. The middle tree consists of the sub-tree rooted at the current node. These three sets are updated down the access path while keeping the splay operations in check. Another method, semisplaying, modifies the zig-zig case to reduce the amount of restructuring done in all operations.[1][6]
Below there is an implementation of splay trees in C++, which uses pointers to represent each node on the tree. This implementation is based on bottom-up splaying version and uses the second method of deletion on a splay tree. Also, unlike the above definition, this C++ version does not splay the tree on finds – it only splays on insertions and deletions, and the find operation, therefore, has linear time complexity.
#include <functional>
#ifndef SPLAY_TREE
#define SPLAY_TREE
template<typename T, typename Comp = std::less<T>>
class splay_tree {
private:
Comp comp;
unsigned long p_size;
struct node {
node *left, *right;
node *parent;
T key;
node(const T& init = T()) : left(nullptr), right(nullptr), parent(nullptr), key(init) { }
~node() {
}
} *root;
void left_rotate(node *x) {
node *y = x->right;
if (y) {
x->right = y->left;
if (y->left) y->left->parent = x;
y->parent = x->parent;
}
if (!x->parent) root = y;
else if (x == x->parent->left) x->parent->left = y;
else x->parent->right = y;
if (y) y->left = x;
x->parent = y;
}
void right_rotate(node *x) {
node *y = x->left;
if (y) {
x->left = y->right;
if (y->right) y->right->parent = x;
y->parent = x->parent;
}
if (!x->parent) root = y;
else if (x == x->parent->left) x->parent->left = y;
else x->parent->right = y;
if (y) y->right = x;
x->parent = y;
}
void splay(node *x) {
while (x->parent) {
if (!x->parent->parent) {
if (x->parent->left == x) right_rotate(x->parent);
else left_rotate(x->parent);
} else if (x->parent->left == x && x->parent->parent->left == x->parent) {
right_rotate(x->parent->parent);
right_rotate(x->parent);
} else if (x->parent->right == x && x->parent->parent->right == x->parent) {
left_rotate(x->parent->parent);
left_rotate(x->parent);
} else if (x->parent->left == x && x->parent->parent->right == x->parent) {
right_rotate(x->parent);
left_rotate(x->parent);
} else {
left_rotate(x->parent);
right_rotate(x->parent);
}
}
}
void replace(node *u, node *v) {
if (!u->parent) root = v;
else if (u == u->parent->left) u->parent->left = v;
else u->parent->right = v;
if (v) v->parent = u->parent;
}
node* subtree_minimum(node *u) {
while (u->left) u = u->left;
return u;
}
node* subtree_maximum(node *u) {
while (u->right) u = u->right;
return u;
}
public:
splay_tree() : root(nullptr), p_size(0) { }
void insert(const T &key) {
node *z = root;
node *p = nullptr;
while (z) {
p = z;
if (comp(z->key, key)) z = z->right;
else z = z->left;
}
z = new node(key);
z->parent = p;
if (!p) root = z;
else if (comp(p->key, z->key)) p->right = z;
else p->left = z;
splay(z);
p_size++;
}
node* find(const T &key) {
node *z = root;
while (z) {
if (comp(z->key, key)) z = z->right;
else if (comp(key, z->key)) z = z->left;
else return z;
}
return nullptr;
}
void erase(const T &key) {
node *z = find(key);
if (!z) return;
splay(z);
if (!z->left) replace(z, z->right);
else if (!z->right) replace(z, z->left);
else {
node *y = subtree_minimum(z->right);
if (y->parent != z) {
replace(y, y->right);
y->right = z->right;
y->right->parent = y;
}
replace(z, y);
y->left = z->left;
y->left->parent = y;
}
delete z;
p_size--;
}
/* //the alternative implementation
void erase(const T &key) {
node *z = find(key);
if (!z) return;
splay(z);
node *s = z->left;
node *t = z->right;
delete z;
node *sMax = NULL;
if (s) {
s->parent = NULL;
sMax = subtree_maximum(s);
splay(sMax);
root = sMax;
}
if (t) {
if (s)
sMax->right = t;
else
root = t;
t->parent = sMax;
}
p_size--;
}
*/
const T& minimum() { return subtree_minimum(root)->key; }
const T& maximum() { return subtree_maximum(root)->key; }
bool empty() const { return root == nullptr; }
unsigned long size() const { return p_size; }
};
#endif // SPLAY_TREE
Analysis
[edit]A simple amortized analysis of static splay trees can be carried out using the potential method. Define:
- size(r) = the number of nodes in the sub-tree rooted at node r (including r).
- rank(r) = log2(size(r)).
- Φ = the sum of the ranks of all the nodes in the tree.
Φ will tend to be high for poorly balanced trees and low for well-balanced trees.
To apply the potential method, we first calculate ΔΦ: the change in the potential caused by a splay operation. We check each case separately. Denote by rank' the rank function after the operation. x, p and g are the nodes affected by the rotation operation (see figures above).
Zig step
[edit]ΔΦ = rank'(p) − rank(p) + rank'(x) − rank(x) [since only p and x change ranks] = rank'(p) − rank(x) [since rank'(x)=rank(p)] ≤ rank'(x) − rank(x) [since rank'(p)<rank'(x)]
Zig-zig step
[edit]ΔΦ = rank'(g) − rank(g) + rank'(p) − rank(p) + rank'(x) − rank(x) = rank'(g) + rank'(p) − rank(p) − rank(x) [since rank'(x)=rank(g)] ≤ rank'(g) + rank'(x) − 2 rank(x) [since rank(x)<rank(p) and rank'(x)>rank'(p)] ≤ 3(rank'(x)−rank(x)) − 2 [due to the concavity of the log function]
Zig-zag step
[edit]ΔΦ = rank'(g) − rank(g) + rank'(p) − rank(p) + rank'(x) − rank(x) ≤ rank'(g) + rank'(p) − 2 rank(x) [since rank'(x)=rank(g) and rank(x)<rank(p)] ≤ 3(rank'(x)−rank(x)) − 2 [due to the concavity of the log function]
The amortized cost of any operation is ΔΦ plus the actual cost. The actual cost of any zig-zig or zig-zag operation is 2 since there are two rotations to make. Hence:
amortized-cost = cost + ΔΦ ≤ 3(rank'(x)−rank(x))
When summed over the entire splay operation, this telescopes to 1 + 3(rank(root)−rank(x)) which is O(log n), since we use The Zig operation at most once and the amortized cost of zig is at most 1+3(rank'(x)−rank(x)).
So now we know that the total amortized time for a sequence of m operations is:
To go from the amortized time to the actual time, we must add the decrease in potential from the initial state before any operation is done (Φi) to the final state after all operations are completed (Φf).
where the big O notation can be justified by the fact that for every node x, the minimum rank is 0 and the maximum rank is log(n).
Now we can finally bound the actual time:
Weighted analysis
[edit]The above analysis can be generalized in the following way.
- Assign to each node r a weight w(r).
- Define size(r) = the sum of weights of nodes in the sub-tree rooted at node r (including r).
- Define rank(r) and Φ exactly as above.
The same analysis applies and the amortized cost of a splaying operation is again:
where W is the sum of all weights.
The decrease from the initial to the final potential is bounded by:
since the maximum size of any single node is W and the minimum is w(x).
Hence the actual time is bounded by:
Performance theorems
[edit]There are several theorems and conjectures regarding the worst-case runtime for performing a sequence S of m accesses in a splay tree containing n elements.
Balance Theorem—The cost of performing the sequence S is .
Take a constant weight, e.g. for every node x. Then .
This theorem implies that splay trees perform as well as static balanced binary search trees on sequences of at least n accesses.[1]
Static Optimality Theorem—Let be the number of times element x is accessed in S. If every element is accessed at least once, then the cost of performing S is
Let . Then .
This theorem implies that splay trees perform as well as an optimum static binary search tree on sequences of at least n accesses.[7] They spend less time on the more frequent items.[1] Another way of stating the same result is that, on input sequences where the items are drawn independently at random from a non-uniform probability distribution on n items, the amortized expected (average case) cost of each access is proportional to the entropy of the distribution.[8]
Static Finger Theorem—Assume that the items are numbered from 1 through n in ascending order. Let f be any fixed element (the 'finger'). Then the cost of performing S is .
Let . Then . The net potential drop is O (n log n) since the weight of any item is at least .[1]
Dynamic Finger Theorem—Assume that the 'finger' for each step accessing an element y is the element accessed in the previous step, x. The cost of performing S is .[9][10]
Working Set Theorem—At any time during the sequence, let be the number of distinct elements accessed before the previous time element x was accessed. The cost of performing S is
Let . Note that here the weights change during the sequence. However, the sequence of weights is still a permutation of . So as before . The net potential drop is O (n log n).
This theorem is equivalent to splay trees having key-independent optimality.[1]
Dynamic optimality conjecture
[edit]In addition to the proven performance guarantees for splay trees there is an unproven conjecture of great interest from the original Sleator and Tarjan paper. This conjecture is known as the dynamic optimality conjecture and it basically claims that splay trees perform as well as any other binary search tree algorithm up to a constant factor.
- Dynamic Optimality Conjecture:[1] Let be any binary search tree algorithm that accesses an element by traversing the path from the root to at a cost of , and that between accesses can make any rotations in the tree at a cost of 1 per rotation. Let be the cost for to perform the sequence of accesses. Then the cost for a splay tree to perform the same accesses is .
There are several corollaries of the dynamic optimality conjecture that remain unproven:
- Traversal Conjecture:[1] Let and be two splay trees containing the same elements. Let be the sequence obtained by visiting the elements in in preorder (i.e., depth first search order). The total cost of performing the sequence of accesses on is .
- Deque Conjecture:[11][13][14] Let be a sequence of double-ended queue operations (push, pop, inject, eject). Then the cost of performing on a splay tree is .
- Split Conjecture:[6] Let be any permutation of the elements of the splay tree. Then the cost of deleting the elements in the order , splitting each tree into two separate trees at each deleted item, is .
Variants
[edit]In order to reduce the number of restructuring operations, it is possible to replace the splaying with semi-splaying, in which an element is splayed only halfway towards the root.[1][2]
Another way to reduce restructuring is to do full splaying, but only in some of the access operations – only when the access path is longer than a threshold, or only in the first m access operations.[1]
The CBTree augments the splay tree with access counts at each node and uses them to restructure infrequently. A variant of the CBTree called the LazyCBTree does at most one rotation on each lookup. This is used along with an optimistic hand-over-hand validation scheme to make a concurrent self-adjusting tree.[15]
Using pointer-compression techniques,[16] it is possible to construct a succinct splay tree.
See also
[edit]- AVL tree
- B-tree
- Finger tree
- Geometry of binary search trees
- Iacono's working set structure
- Link/cut tree
- List of data structures
- Scapegoat tree
- Splaysort, a sorting algorithm using splay trees
- T-tree
- Treap
- Tree rotation
- Trees
- Zipper (data structure)
Notes
[edit]- ^ a b c d e f g h i j k l m n Sleator & Tarjan 1985.
- ^ a b c Brinkmann, Degraer & De Loof 2009.
- ^ Goodrich, Tamassia & Goldwasser 2014.
- ^ Albers & Karpinski 2002.
- ^ Allen & Munro 1978.
- ^ a b Lucas 1991.
- ^ Knuth 1997, p. 478
- ^ Grinberg et al. (1995).
- ^ Cole et al. 2000.
- ^ Cole 2000.
- ^ a b Tarjan 1985.
- ^ Elmasry 2004.
- ^ Pettie 2008.
- ^ Sundar 1992.
- ^ Afek et al. 2014
- ^ Bender et al. 2023.
References
[edit]- Afek, Yehuda; Kaplan, Haim; Korenfeld, Boris; Morrison, Adam; Tarjan, Robert E. (2014). "The CB tree: a practical concurrent self-adjusting search tree". Distributed Computing. 27 (6): 393–417. doi:10.1007/s00446-014-0229-0.
- Albers, Susanne; Karpinski, Marek (28 February 2002). "Randomized Splay Trees: Theoretical and Experimental Results" (PDF). Information Processing Letters. 81 (4): 213–221. doi:10.1016/s0020-0190(01)00230-7.
- Bose, Prosenjit; Douïeb, Karim; Dujmović, Vida; Fagerberg, Rolf (2010). "An O(log log n)-Competitive Binary Search Tree with Optimal Worst-Case Access Times". In Kaplan, H. (ed.). Algorithm Theory - SWAT 2010. Lecture Notes in Computer Science. Vol. 6139. pp. 38–49. arXiv:1003.0139. doi:10.1007/978-3-642-13731-0_5. ISBN 978-3-642-13730-3.
- Allen, Brian; Munro, Ian (October 1978). "Self-organizing binary search trees". Journal of the ACM. 25 (4): 526–535. doi:10.1145/322092.322094. S2CID 15967344.
- Brinkmann, Gunnar; Degraer, Jan; De Loof, Karel (January 2009). "Rehabilitation of an unloved child: semi-splaying" (PDF). Software: Practice and Experience. 39 (1): 33–45. CiteSeerX 10.1.1.84.790. doi:10.1002/spe.v39:1. hdl:11382/102133.
The results show that semi-splaying, which was introduced in the same paper as splaying, performs better than splaying under almost all possible conditions. This makes semi-splaying a good alternative for all applications where normally splaying would be applied. The reason why splaying became so prominent while semi-splaying is relatively unknown and much less studied is hard to understand.
- Cole, Richard; Mishra, Bud; Schmidt, Jeanette; Siegel, Alan (January 2000). "On the Dynamic Finger Conjecture for Splay Trees. Part I: Splay Sorting log n-Block Sequences". SIAM Journal on Computing. 30 (1): 1–43. CiteSeerX 10.1.1.36.4558. doi:10.1137/s0097539797326988.
- Cole, Richard (January 2000). "On the Dynamic Finger Conjecture for Splay Trees. Part II: The Proof". SIAM Journal on Computing. 30 (1): 44–85. CiteSeerX 10.1.1.36.2713. doi:10.1137/S009753979732699X.
- Elmasry, Amr (April 2004). "On the sequential access theorem and Deque conjecture for splay trees". Theoretical Computer Science. 314 (3): 459–466. doi:10.1016/j.tcs.2004.01.019.
- Goodrich, Michael; Tamassia, Roberto; Goldwasser, Michael (2014). Data Structures and Algorithms in Java (6 ed.). Wiley. p. 506. ISBN 978-1-118-77133-4.
- Grinberg, Dennis; Rajagopalan, Sivaramakrishnan; Venkatesan, Ramarathnam; Wei, Victor K. (1995). "Splay trees for data compression". In Clarkson, Kenneth L. (ed.). Proceedings of the Sixth Annual ACM-SIAM Symposium on Discrete Algorithms, 22–24 January 1995. San Francisco, California, USA. ACM/SIAM. pp. 522–530.
Average depth of access in a splay tree is proportional to the entropy.
- Knuth, Donald (1997). The Art of Computer Programming. Vol. 3: Sorting and Searching (3rd ed.). Addison-Wesley. p. 478. ISBN 0-201-89685-0.
The time needed to access data in a splay tree is known to be at most a small constant multiple of the access time of a statically optimum tree, when amortized over any series of operations.
- Lucas, Joan M. (1991). "On the Competitiveness of Splay Trees: Relations to the Union-Find Problem". On-line Algorithms: Proceedings of a DIMACS Workshop, February 11–13, 1991. Series in Discrete Mathematics and Theoretical Computer Science. Vol. 7. Center for Discrete Mathematics and Theoretical Computer Science. pp. 95–124. ISBN 0-8218-7111-0.
- Pettie, Seth (2008). "Splay Trees, Davenport-Schinzel Sequences, and the Deque Conjecture". Proc. 19th ACM-SIAM Symposium on Discrete Algorithms (PDF). pp. 1115–1124. arXiv:0707.2160.
- Sleator, Daniel D.; Tarjan, Robert E. (1985). "Self-Adjusting Binary Search Trees" (PDF). Journal of the ACM. 32 (3): 652–686. doi:10.1145/3828.3835. S2CID 1165848.
- Sundar, Rajamani (1992). "On the Deque conjecture for the splay algorithm". Combinatorica. 12 (1): 95–124. doi:10.1007/BF01191208. S2CID 27422556.
- Tarjan, Robert E. (1985). "Sequential access in splay trees takes linear time". Combinatorica. 5 (4): 367–378. doi:10.1007/BF02579253. S2CID 34757821.
- Bender, Michael A.; Conway, Alex; Farach-Colton, Martin; Kuszmaul, William; Tagliavini, Guido (2023). "Tiny Pointers". Proceedings of the 2023 Annual ACM-SIAM Symposium on Discrete Algorithms (SODA): 477–508. doi:10.1137/1.9781611977554.ch21. ISBN 978-1-61197-755-4. S2CID 244709005.
External links
[edit]Splay tree
View on GrokipediaDefinition and Background
Definition
A splay tree is a self-adjusting binary search tree designed to optimize access times for frequently used elements by reorganizing the tree structure after each operation. Unlike traditional balanced binary search trees, a splay tree does not maintain explicit invariants such as height restrictions or color rules; instead, it relies on a heuristic called splaying to move recently accessed nodes to the root, thereby improving the amortized efficiency of subsequent operations. This self-adjustment ensures that the tree adapts dynamically to patterns in the access sequence without requiring prior knowledge of the data distribution.[1] At its core, a splay tree adheres to the fundamental properties of a binary search tree: each node stores a unique key, with all keys in the left subtree being strictly less than the node's key and all keys in the right subtree being strictly greater. The basic node structure consists of the key value, pointers to the left and right child nodes, and optionally a parent pointer to support bottom-up implementations of the splay operation. Rotations performed during splaying preserve this in-order traversal property, ensuring that the tree remains a valid binary search tree after every insertion, deletion, search, or other access.[1][3] To illustrate, consider a simple splay tree with keys 1, 2, and 3 arranged in a right-skewed chain, where 1 is the root, 2 is its right child, and 3 is the right child of 2. This configuration forms a degenerate tree with height 2. After performing a search on key 3, which triggers a splay operation, node 3 is rotated to the root, resulting in root 3 with 2 as its left child and 1 as the left child of 2. The tree is now left-skewed with height still 2, but the accessed element is positioned at the root for faster future retrievals.[1][3]History
The splay tree was invented in 1985 by Daniel D. Sleator and Robert E. Tarjan while they were researchers at AT&T Bell Laboratories. Their work was motivated by the desire to create an efficient dynamic dictionary data structure that leverages locality of reference in access sequences, allowing recently accessed elements to be retrieved more quickly without the overhead of explicit balancing mechanisms found in traditional binary search trees.[1] Sleator and Tarjan introduced the splay tree in their seminal paper "Self-Adjusting Binary Search Trees," published in the Journal of the Association for Computing Machinery. This publication detailed the splaying operation as a simple heuristic inspired by earlier self-adjusting techniques, such as the move-to-front rule for linear lists and path compression in union-find structures, which reorganize data based on usage patterns to improve amortized performance.[4][1] In the context of the 1980s, splay trees emerged as a response to fixed-balance trees like AVL trees and red-black trees, which maintain O(log n) worst-case time but require additional space for balance information and more complex implementations during insertions and deletions. Splay trees prioritized simplicity and adaptability, achieving comparable amortized efficiency through self-adjustment. Key milestones include their integration into the BSD kernel in the early 2000s (specifically, FreeBSD 5.0 in 2003) for virtual memory management, enhancing caching performance in operating systems. Later developments, such as the tango tree in the 2000s, built on splay tree concepts to explore stronger optimality bounds. Recent theoretical advancements, including progress toward the dynamic optimality conjecture in works from the late 2010s, have confirmed aspects of splay trees' efficiency for arbitrary access sequences.[1][5][6][7]Properties
Advantages
Splay trees achieve an amortized time complexity of O(log n) for search, insertion, and deletion operations on an n-node tree, where the splaying mechanism brings recently accessed nodes closer to the root, thereby exploiting access locality to improve subsequent operations.[1] Compared to height-balanced trees such as AVL or red-black trees, splay trees offer a simpler implementation, as they require no explicit balance factors, color attributes, or additional rotations beyond the splaying process itself.[1] Furthermore, they maintain space efficiency with O(n overall storage, using no extra metadata per node beyond the standard binary search tree pointers and keys.[8] Splay trees are particularly adaptive to access patterns exhibiting temporal locality, performing well in scenarios like caching where frequently accessed elements benefit from reduced path lengths after splaying.[1] In empirical evaluations on real-world workloads, such as those in Mozilla, VMware, and Squid applications, splay trees have demonstrated 23%–40% faster performance than red-black trees, attributed to fewer rotations and better handling of clustered or sequential accesses.[8]Disadvantages
Splay trees exhibit a worst-case time complexity of O(n for individual operations, such as when accessing a node in a degenerate tree that forms a linear chain, requiring up to n rotations during the splay step to bring the accessed node to the root.[1] This lack of a guaranteed O(log n) bound per operation distinguishes splay trees from height-balanced variants like AVL or red-black trees, rendering them unsuitable for real-time systems where predictable worst-case performance is essential, as individual operations can become prohibitively expensive.[1][9] The splaying mechanism introduces higher constant factors compared to standard binary search tree operations, since even in a well-balanced tree, accessing a node typically triggers multiple rotations—often several per access—incurring additional overhead from these structural adjustments.[10] Splay trees are particularly sensitive to access patterns, performing poorly on uniformly random sequences or adversarial inputs that lack temporal locality, where the frequent restructuring fails to yield efficiency gains and can even degrade performance relative to simpler balanced trees.[11]Operations
Splaying
Splaying is the core operation in a splay tree that rearranges the tree structure after accessing a node, promoting that node to the root through a sequence of tree rotations while maintaining the binary search tree (BST) in-order traversal property. This process amortizes the cost of future accesses by bringing recently used nodes closer to the root, though the immediate cost of splaying can be linear in the tree height. The rotations used in splaying are the same as those in AVL trees or other self-balancing BSTs, ensuring no violation of BST invariants. Two primary approaches exist for implementing splaying: bottom-up and top-down. The bottom-up method starts at the accessed node and performs rotations upward toward the root, typically without requiring parent pointers in the node structure, but it involves single or double rotations based on the configuration with the parent and grandparent. In contrast, the top-down approach simulates the process from the root downward using parent pointers to track and rotate nodes as it descends, avoiding the need for double rotations but increasing memory overhead per node. The original splay tree formulation by Sleator and Tarjan favored the bottom-up variant for its simplicity in pointer-based implementations.[1] The general algorithm for bottom-up splaying operates iteratively: while the accessed node is not the root, it examines the positions relative to its parent and grandparent (if they exist). If has no parent, it is already the root and splaying terminates. If has a parent but no grandparent, a single "zig" rotation is performed between and . Otherwise, if and are both left (or both right) children of their parents, a "zig-zig" double rotation is applied: first rotate with , then rotate with . If is a left child and a right child (or vice versa), a "zig-zag" double rotation occurs: first rotate with , then rotate (now sibling to ) with . This repeats until reaches the root, preserving the BST order at each step.[1] Here is pseudocode for the bottom-up splay operation, assuming nodes have left and right child pointers and the tree root is maintained separately:function splay(x, [root](/page/Root)):
while x != root:
p = [parent](/page/Parent)(x) // Assume parent pointers or traversal to find
if p is null:
break // x is root
g = [parent](/page/Parent)(p)
if g is null:
// zig: single [rotation](/page/Rotation)
rotate(x, p)
update_root_if_needed(root, x)
break
if (x == left(p) and p == left(g)) or (x == right(p) and p == right(g)):
// zig-zig: double [rotation](/page/Rotation)
rotate(p, g)
rotate(x, p)
update_root_if_needed(root, x)
else:
// zig-zag: double [rotation](/page/Rotation)
rotate(x, p)
rotate(x, g)
update_root_if_needed(root, x)
return x // Now the new root
function splay(x, [root](/page/Root)):
while x != root:
p = [parent](/page/Parent)(x) // Assume parent pointers or traversal to find
if p is null:
break // x is root
g = [parent](/page/Parent)(p)
if g is null:
// zig: single [rotation](/page/Rotation)
rotate(x, p)
update_root_if_needed(root, x)
break
if (x == left(p) and p == left(g)) or (x == right(p) and p == right(g)):
// zig-zig: double [rotation](/page/Rotation)
rotate(p, g)
rotate(x, p)
update_root_if_needed(root, x)
else:
// zig-zag: double [rotation](/page/Rotation)
rotate(x, p)
rotate(x, g)
update_root_if_needed(root, x)
return x // Now the new root
rotate function performs a standard BST rotation (left or right depending on child position), and update_root_if_needed adjusts the tree's root reference if the original root was rotated. This implementation handles null parents and root cases explicitly to prevent errors.
Consider a small splay tree with keys 1, 2, 3, 4, 5 in in-order, initially structured as root 3 (left: 2 (left: 1)), right: 5 (left: 4). To splay key 1:
- Node 1's parent is 2, grandparent is 3 (both left children), so zig-zig: first right-rotate on 3, promoting 2 to root (left 1, right 3 right 5 left 4); then right-rotate on 2, promoting 1 to root (right 2 right 3 right 5 left 4).
- Node 4's parent is 5 (right child of 3), 4 is left child of 5, so zig-zag: first right-rotate on 5, making 4 the right child of 3 (right 5); then left-rotate on 3, promoting 4 to root (left 3 left 2 left 1, right 5).
Insertion and Deletion
In splay trees, the core dictionary operations—search, insertion, and deletion—are adapted from standard binary search trees (BSTs) by incorporating splaying after the initial traversal or modification to move the accessed or affected node to the root, ensuring amortized efficiency.[1] This approach leverages the self-adjusting property to reduce future access times for recently used elements without explicit balancing.[1] The operations maintain the BST invariant (left subtree keys less than node key, right subtree keys greater) throughout.[1] Insertion in a splay tree proceeds by first performing a standard BST insertion: traverse from the root following the search path to locate the null pointer where the new key belongs, and attach the new node as a leaf there.[1] Immediately after, splay the newly inserted node to the root using the splaying procedure.[1] An alternative formulation uses the split operation to decompose the tree at the insertion point, creates the new singleton node, and then joins the parts, but the effect is equivalent in terms of structure and cost.[1] To illustrate, consider an initially empty splay tree. Inserting the key 10 creates a single-node tree with 10 at the root. Next, inserting 5 traverses left from 10 (since 5 < 10), attaches 5 as the left child, and splays 5 to the root, resulting in 5 as root with 10 as right child. Inserting 15 then traverses right from 5 to 10 (15 > 5, 15 > 10), attaches 15 as right child of 10, and splays 15 to the root via zig-zig (both right children), yielding root 15 left 10 left 5. This restructuring brings the new node to prominence for potential subsequent accesses.[1] Deletion begins by searching for the target key, which splays it to the root if found (or splays the last probed node if not).[1] With the node at the root, remove it by joining its left and right subtrees into a single tree, preserving the BST order.[1] The join typically splays the maximum node (rightmost) in the left subtree to become the new root if the left subtree is non-empty, then attaches the original right subtree as its right child; if no left subtree, the right subtree becomes the new tree directly.[1] If the root has no children, deletion simply empties the tree.[12] For example, starting from the tree after the above insertions (root 15 left 10 left 5), deleting 10 splays 10 to root via single zig (right-rotate on 15), resulting in root 10 left 5 right 15; then joins left (5) and right (15) by splaying 5 (max of left) to root and attaching 15 as right, resulting in root 5 with right 15. This maintains balance heuristically through the splaying.[1] The search operation follows BST traversal rules: start at the root and descend left or right based on key comparisons until reaching the target node or a null pointer indicating absence.[1] If the key is found, splay that node to the root; if not, splay the last node visited (the potential insertion point) to the root instead.[1] This ensures that future searches near the probed path benefit from the adjustment.[1] Splay trees assume unique keys and do not inherently support duplicates, as the BST invariant relies on strict ordering.[1] In practice, encountering a duplicate during insertion typically results in ignoring the new key or replacing the existing node's value, depending on the implementation policy for set or map semantics.[13]Split and Join
In splay trees, the split operation decomposes a single splay tree into two independent splay trees and , such that all keys in are less than or equal to a given key , and all keys in are strictly greater than . This is accomplished by first splaying the node with key (or its predecessor/successor if is absent) to the root of , which brings the relevant splitting point to the top of the tree. Once splayed, consists of the root and its entire left subtree (possibly including the root if its key equals ), while is detached as the right subtree (or adjusted accordingly if the root's key exceeds ).[1] The join operation, conversely, combines two splay trees and into a single splay tree , under the precondition that every key in is strictly less than every key in . To perform the join, the maximum key in is splayed to its root, ensuring the largest element is at the top. The root of is then attached directly as the right child of this new root in , forming the combined tree without further rotations.[1] Both operations leverage the splaying mechanism for efficiency and run in amortized time, where is the number of nodes in the tree, due to the amortized cost of splaying combined with constant-time subtree detachment or attachment at the root.[1] The following pseudocode outlines the split operation (assuming standard splay tree node structure with left and right children):function split(k, T):
if T is empty:
return (empty, empty)
splay(k, T) // Splay k (or successor/predecessor) to root
root = T.root
if root.key <= k:
T_R = root.right
root.right = empty
return (T, T_R)
else:
T_L = root.left
root.left = empty
return (T_L, T)
function split(k, T):
if T is empty:
return (empty, empty)
splay(k, T) // Splay k (or successor/predecessor) to root
root = T.root
if root.key <= k:
T_R = root.right
root.right = empty
return (T, T_R)
else:
T_L = root.left
root.left = empty
return (T_L, T)
function join(T_L, T_R):
if T_L is empty:
return T_R
if T_R is empty:
return T_L
splay_max(T_L) // Splay the maximum key to root of T_L
T_L.root.right = T_R.root
return T_L
function join(T_L, T_R):
if T_L is empty:
return T_R
if T_R is empty:
return T_L
splay_max(T_L) // Splay the maximum key to root of T_L
T_L.root.right = T_R.root
return T_L
splay_max(T) splays the rightmost node (maximum key) to the root by repeatedly splaying right children.[1]
These operations are particularly efficient for scenarios involving dynamic set manipulations, such as merging disjoint ordered sets or supporting range queries by temporarily decomposing the tree into key-ordered segments. For instance, to extract keys in , one can split at to isolate the lower portion, then split the remainder at to obtain the range as a separate splay tree, process it, and rejoin the parts.[1]
As an illustrative example, consider a splay tree with keys {1, 3, 5, 7} initially structured as root 5 (left: 3 with left 1; right: 7). Splitting at key 4 splays 3 (predecessor) to the root, yielding with {1, 3} (root 3, left 1) and with {5, 7} (root 5, right 7). Joining and splays 3 (max in ) to root and attaches as its right subtree, resulting in root 3 left 1 right 5 right 7. This demonstrates how split and join preserve the binary search tree property while enabling modular tree handling.[1]
Analysis
Splaying Steps
The splaying process in a splay tree consists of a sequence of primitive rotation operations—known as zig, zig-zig, and zig-zag—that incrementally move the accessed node toward the root while preserving the binary search tree (BST) property, ensuring that in-order traversal remains unchanged. These steps are applied bottom-up along the access path, with each rotation adjusting parent-child relationships to promote the node without violating the ordering invariant. Although splay trees do not enforce a strict heap ordering, the rotations during ascent effectively balance the tree by deepening subtrees of less recently accessed nodes, contributing to amortized efficiency as analyzed elsewhere.[1]Zig Step
The zig step is the simplest primitive, performed as a single rotation when the target node is a direct child of the current root. This terminal operation brings to the root position in constant time. Specifically, if is the left child of the root , a right rotation is applied on the edge between and ; conversely, if is the right child, a left rotation is used. Pre-rotation configuration (assuming as left child of root ): p
/ \
x C
/ \
A B
p
/ \
x C
/ \
A B
x
/ \
A p
/ \
B C
x
/ \
A p
/ \
B C
if p(x) is root then
if x is left child of p(x) then rotate_right(p(x))
else rotate_left(p(x))
if p(x) is root then
if x is left child of p(x) then rotate_right(p(x))
else rotate_left(p(x))
rotate_right(y) promotes the left child of by adjusting pointers: the left child of becomes the new parent, with subtrees reattached to preserve order.[1]
Zig-Zig Step
The zig-zig step applies a double rotation when the target node and its parent are both left children (or both right children) of their respective parents, and is not the root. This configuration allows to ascend two levels in a balanced manner, first rotating the edge between and the grandparent , then rotating the edge between and the new parent (formerly ). Pre-rotation configuration (both left children case, with grandparent ): g
/
p
/
x
/ \
A B
g
/
p
/
x
/ \
A B
x
/ \
A p
/ \
B g
/
C (subtree of g)
x
/ \
A p
/ \
B g
/
C (subtree of g)
if p(x) is left child of g(x) then
rotate_right(g(x))
rotate_right(p(x))
else if p(x) is right child of g(x) then
rotate_left(g(x))
rotate_left(p(x))
if p(x) is left child of g(x) then
rotate_right(g(x))
rotate_right(p(x))
else if p(x) is right child of g(x) then
rotate_left(g(x))
rotate_left(p(x))
Zig-Zag Step
The zig-zag step uses a double rotation for the opposing-child case, where is a left child of but is a right child of , or vice versa, and is not the root. This "zig-zag" pattern first rotates the edge between and to make a sibling of its former parent, then rotates the edge between and the new parent (formerly ) to promote two levels. Pre-rotation configuration ( left of , right of ): g
\
p
/
x
/ \
A B
g
\
p
/
x
/ \
A B
x
/ \
A g
/ \
B p
/
C (subtree of p)
x
/ \
A g
/ \
B p
/
C (subtree of p)
if x is left child of p(x) and p(x) is right child of g(x) then
rotate_right(p(x))
rotate_left(g(x))
else if x is right child of p(x) and p(x) is left child of g(x) then
rotate_left(p(x))
rotate_right(g(x))
if x is left child of p(x) and p(x) is right child of g(x) then
rotate_right(p(x))
rotate_left(g(x))
else if x is right child of p(x) and p(x) is left child of g(x) then
rotate_left(p(x))
rotate_right(g(x))
Amortized Analysis
The amortized analysis of splay trees focuses on the average performance over a sequence of operations, rather than the worst-case cost of individual operations, which can reach in a tree with nodes due to deep, unbalanced structures. This approach aggregates costs across multiple operations to demonstrate that splay trees maintain efficiency in practice, even if occasional operations are expensive. By employing the potential method, the analysis accounts for "stored work" in the tree's structure that offsets high costs during splaying.[1] The potential function for a splay tree is defined as the sum over all nodes of , where is the size of the subtree rooted at (including itself). This non-negative function measures the tree's "disorder" or depth-related inefficiency. The amortized cost of an operation is the actual time plus the change in potential , ensuring that the total amortized cost over operations bounds the total actual cost. During splaying, rotations typically decrease the potential by restructuring the tree to bring the accessed node closer to the root, with each rotation costing constant time but yielding a net potential drop that amortizes the effort.[1] The cost of splaying a node to the root is bounded by amortized time, as the potential decrease during the sequence of rotations compensates for the number of steps, which is at most in aggregate. Specifically, each single rotation or double rotation in the splay reduces the potential by an amount proportional to the rank increase of , leading to an overall amortized bound of at most for accessing any node. This holds because the potential change ensures that expensive splays are "prepaid" by prior operations that built up the potential.[1] All major splay tree operations—search, insertion, deletion, split, and join—achieve amortized time complexity, as each involves at most a constant number of non-splay steps plus one splay operation. For instance, insertion splays the new node after attaching it, and deletion splays the target before removal, both leveraging the splay bound. Over operations on an -node tree, the total time is , assuming uniform access frequencies.[1] To illustrate, consider a simple splay sequence on a right-skewed tree of three nodes (A root, B right child, C right child of B), accessing C, which requires a zig-zig step consisting of two rotations (assuming unit weights, so sizes are node counts). Initially, sizes are , , , so . The first rotation (left rotation on A, the grandparent) brings B to the root, costing 1 unit actual time; new sizes: , , , , potential drop of 1, amortized cost . The second rotation (left rotation on B, now the parent and root) brings C to the root, costing 1; final sizes: , , , , potential increase of 1, amortized cost . Total actual cost 2, total amortized cost 2, with net potential change 0, showing how potential changes offset the costs over the sequence. This pattern scales, with deeper trees yielding larger drops during splaying.[1]Weighted Path Length
In splay trees, the weighted path length is defined as the sum over all nodes of , where is the fixed weight (often representing access frequency) of node , and is the depth of in the tree.[1] This metric quantifies the total search cost under a weighted access model, as the time to access node is proportional to its depth.[1] Splaying minimizes the weighted path length over a sequence of accesses by repeatedly rotating the accessed node toward the root, thereby reducing the depths of frequently accessed (higher-weight) nodes while potentially increasing depths of less frequent ones.[1] This self-adjustment ensures that nodes with higher weights tend to occupy shallower positions, lowering the overall weighted path length amortized across operations.[1] To analyze this, the potential function is , where the sum is over all nodes in the tree , and the rank with denoting the size of the subtree rooted at , defined as the sum of weights of all nodes in that subtree.[1] This potential, which approximates the logarithm of the weighted path length up to additive constants, increases when the tree becomes more unbalanced but decreases sufficiently during splaying to bound costs.[1] The derivation proceeds by charging the actual cost of each rotation in a splay to changes in potential. For a splay operation that brings node to the root of tree with root rank , the amortized cost is at most .[1] Specifically, a single zig rotation changes the potential by at most ; a zig-zig by at most ; and a zig-zag by at most , where primes denote values after the rotation.[1] Summing over the rotations in a splay yields an amortized cost of , as for uniform weights, ensuring the weighted path length remains low on average.[1]Theorems and Conjectures
Performance Theorems
The Balance Theorem establishes that any sequence of accesses in an -node splay tree requires time in total.[4] This bound matches the performance of a balanced binary search tree over a sequence of at least operations, ensuring that splay trees remain efficient even without prior knowledge of access patterns. The proof relies on an amortized analysis using a potential function based on the tree's structure, where each splay operation is charged at most amortized time, with an initial potential of that bounds the total cost across all operations.[4] The Static Optimality Theorem provides a tighter bound for scenarios with known, fixed access frequencies. If each of the items is accessed times with total accesses , the total access time is , assuming every item is accessed at least once.[4] This demonstrates that splay trees perform within a constant factor of an optimal static binary search tree tailored to those frequencies, as the bound approximates the entropy of the access distribution. The proof sketch employs a weighted potential function where each node is assigned weight , leading to an amortized splay cost of per access, with the total potential change bounded by .[4] The Static Finger Theorem extends efficiency to cases with a designated "finger" pointer to a fixed item . For a sequence of accesses to items , the total time is , where distances are measured in the key order.[4] This implies faster operations for accesses near the finger, akin to finger search trees, by leveraging the splaying mechanism to reduce path lengths relative to the fixed reference. The analysis uses a potential function incorporating distances to the finger, bounding the amortized cost per access by .[4] These theorems collectively guarantee that splay trees are competitive with optimal offline binary search trees for static access patterns, using potential functions to compare splaying costs against idealized structures.[4]Dynamic Optimality Conjecture
The dynamic optimality conjecture posits that splay trees achieve near-optimal performance among all binary search trees (BSTs) for any sequence of accesses. Specifically, for any sequence of m successful accesses on an n-node search tree, the total time for splaying is at most O(n) plus a constant factor times the time required by any algorithm that performs each access by traversing from the root to the accessed node (costing one plus the node's depth) and restructures the tree using an arbitrary number of rotations between accesses (each costing one).[1] This conjecture, proposed by Daniel Sleator and Robert Tarjan in their seminal 1985 paper introducing splay trees, implies that splay trees are O(1)-competitive with the optimal offline BST for any access sequence, without requiring prior knowledge of the sequence.[1] Although the full conjecture remains unproven, significant partial confirmations exist. In 2004, Erik Demaine, Dion Harmon, John Iacono, and Mihai Pătraşcu introduced tango trees, which achieve O(log log n)-competitiveness against the optimal offline BST, providing the first sub-logarithmic competitive ratio and marking major progress toward constant competitiveness.[14] Independently, Jérémy Derrien, Julien Clément, and Sylvie Baneyrolles developed multi-splay trees, another O(log log n)-competitive structure that replaces certain components of tango trees with splay trees to improve auxiliary operation bounds.[15] These results confirm the conjecture in restricted settings, such as when access sequences are independent of key orderings, where splay trees are proven dynamically optimal.[14] Empirical studies indicate that splay trees perform consistently close to the optimal offline BST across diverse access patterns, supporting the conjecture's plausibility without counterexamples identified to date.[16] Recent theoretical advances in the 2020s, including work by Caleb Levy and Robert Tarjan, have proven dynamic optimality for splay trees on restricted classes of sequences, such as decomposable or working-set-bound sequences, further narrowing the gap to a full proof.[17] As of 2025, the general case remains open, with no disproof or counterexamples found despite extensive analysis.[18] If proven true, the conjecture would establish splay trees as a universal online BST solution, performing within a constant factor of any possible rotation-based BST—static or adaptive—for arbitrary online access sequences, eliminating the need for sequence-specific tuning.[1]Variants and Implementation
Implementation Techniques
Splay trees can be implemented using either bottom-up or top-down splaying approaches, each with distinct advantages in terms of pointer requirements and traversal efficiency. The bottom-up method, as originally described, involves first searching for the target node from the root and then performing a series of rotations along the access path to bring it to the root, typically requiring parent pointers to facilitate the upward rotations.[1] This approach uses three rotation patterns—zig (single rotation), zig-zig (two consecutive rotations in the same direction), and zig-zag (two rotations in opposite directions)—and is straightforward but incurs the overhead of maintaining parent links.[1] In contrast, the top-down splaying technique avoids parent pointers altogether by tracking the path from the root to the target during the initial search and restructuring the tree in a single downward pass using only zig and zig-zig operations, effectively simulating the rotations without revisiting nodes upward.[19] Top-down implementations are often preferred in environments where memory for parent pointers is a concern, as they reduce storage needs while preserving the amortized performance guarantees.[20] Implementations must carefully handle edge cases to maintain correctness and the binary search tree invariants. For an empty tree, operations like insertion simply allocate a new root node without splaying, as there is no existing structure to adjust.[1] When splaying a single-node tree, no rotations are performed, since the node is already the root, avoiding unnecessary operations.[1] Root changes, which occur after splaying a non-root node to the top, require updating the external root pointer to the new root, ensuring subsequent operations start from the correct entry point.[1] Language-specific considerations influence the choice of data structures and mutation strategies. In C++, nodes are typically represented as structs or classes with pointers to left and right children, allowing efficient in-place rotations via pointer reassignment, which aligns well with the imperative nature of the language.[1] For functional languages like Haskell, splay trees achieve persistency through path copying, where rotations create new nodes along the affected path while sharing unchanged subtrees, enabling immutable versions of the tree after each operation without altering the original. A common optimization to mitigate worst-case deep trees during initial unbalanced phases is semi-splaying, which limits restructuring by moving the accessed node only halfway up the path (e.g., by performing rotations up to the midpoint), reducing rotation overhead while still improving access times for frequent elements.[1] The following pseudocode illustrates a basic bottom-up splay function, focusing on rotation helpers; it assumes nodes have left, right, and parent pointers.function rotate_left(x):
y = x.right
x.right = y.left
if y.left != null:
y.left.parent = x
y.parent = x.parent
if x.parent == null:
root = y
else if x == x.parent.left:
x.parent.left = y
else:
x.parent.right = y
y.left = x
x.parent = y
function rotate_right(x):
y = x.left
x.left = y.right
if y.right != null:
y.right.parent = x
y.parent = x.parent
if x.parent == null:
root = y
else if x == x.parent.right:
x.parent.right = y
else:
x.parent.left = y
y.right = x
x.parent = y
function splay(x):
while x.parent != null:
parent = x.parent
grandparent = parent.parent
if grandparent == null:
// zig
if x == parent.left:
rotate_right(parent)
else:
rotate_left(parent)
else if x == parent.left and parent == grandparent.left:
// zig-zig
rotate_right(grandparent)
rotate_right(parent)
else if x == parent.right and parent == grandparent.right:
// zig-zig
rotate_left(grandparent)
rotate_left(parent)
else:
// zig-zag
if x == parent.left:
rotate_right(parent)
rotate_left(x)
else:
rotate_left(parent)
rotate_right(x)
function rotate_left(x):
y = x.right
x.right = y.left
if y.left != null:
y.left.parent = x
y.parent = x.parent
if x.parent == null:
root = y
else if x == x.parent.left:
x.parent.left = y
else:
x.parent.right = y
y.left = x
x.parent = y
function rotate_right(x):
y = x.left
x.left = y.right
if y.right != null:
y.right.parent = x
y.parent = x.parent
if x.parent == null:
root = y
else if x == x.parent.right:
x.parent.right = y
else:
x.parent.left = y
y.right = x
x.parent = y
function splay(x):
while x.parent != null:
parent = x.parent
grandparent = parent.parent
if grandparent == null:
// zig
if x == parent.left:
rotate_right(parent)
else:
rotate_left(parent)
else if x == parent.left and parent == grandparent.left:
// zig-zig
rotate_right(grandparent)
rotate_right(parent)
else if x == parent.right and parent == grandparent.right:
// zig-zig
rotate_left(grandparent)
rotate_left(parent)
else:
// zig-zag
if x == parent.left:
rotate_right(parent)
rotate_left(x)
else:
rotate_left(parent)
rotate_right(x)







![{\displaystyle O\left[m\log n+n\log n\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/f90f4f6ae11db70bb1c8981020c78d8031a91470)



![{\displaystyle O\left[m+\sum _{x\in tree}q_{x}\log {\frac {m}{q_{x}}}\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/9ed09c13d866de44ee94af14427d4ce34fac0eb2)


![{\displaystyle O\left[m+n\log n+\sum _{x\in sequence}\log(|x-f|+1)\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/09ab9b00273a6335580cbbc91eafb63c0f8bd7ca)



![{\displaystyle O\left[m+n+\sum _{x,y\in sequence}^{m}\log(|y-x|+1)\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/7dfe268a044b7d6bb834ac478b5b02721a2d9144)

![{\displaystyle O\left[m+n\log n+\sum _{x\in sequence}\log(t(x)+1)\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/b779ede85f7e8506bcb63fbca03a676f24e36afd)








![{\displaystyle O[n+A(S)]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/7f5f278631f2a8eeb45687d268a6cd1ec82f0661)




