Hubbry Logo
Balancing selectionBalancing selectionMain
Open search
Balancing selection
Community hub
Balancing selection
logo
7 pages, 0 posts
0 subscribers
Be the first to start a discussion here.
Be the first to start a discussion here.
Contribute something
Balancing selection
Balancing selection
Balancing selection
View on Wikipedia
from Wikipedia

Balancing selection refers to a number of selective processes by which multiple alleles (different versions of a gene) are actively maintained in the gene pool of a population at frequencies larger than expected from genetic drift alone. Balancing selection is rare compared to purifying selection.[1] It can occur by various mechanisms, in particular, when the heterozygotes for the alleles under consideration have a higher fitness than the homozygote.[2] In this way genetic polymorphism is conserved.[3]

Evidence for balancing selection can be found in the number of alleles in a population which are maintained above mutation rate frequencies. All modern research has shown that this significant genetic variation is ubiquitous in panmictic populations.

There are several mechanisms (which are not exclusive within any given population) by which balancing selection works to maintain polymorphism. The two major and most studied are heterozygote advantage and frequency-dependent selection.

Mechanisms

[edit]

Heterozygote advantage

[edit]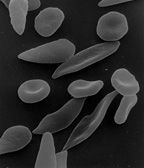
Sickle-shaped red blood cells. This non-lethal condition in heterozygotes is maintained by balancing selection in humans of Africa and India due to its resistance to the malarial parasite.
Malaria versus sickle-cell trait distributions
Main article: Heterozygote advantage

In heterozygote advantage, or heterotic balancing selection, an individual who is heterozygous at a particular gene locus has a greater fitness than a homozygous individual. Polymorphisms maintained by this mechanism are balanced polymorphisms.[4] Due to unexpected high frequencies of heterozygotes, and an elevated level of heterozygote fitness, heterozygotic advantage may also be called "overdominance" in some literature.

A well-studied case is that of sickle cell anemia in humans, a hereditary disease that damages red blood cells. Sickle cell anemia is caused by the inheritance of an allele (HgbS) of the hemoglobin gene from both parents. In such individuals, the hemoglobin in red blood cells is extremely sensitive to oxygen deprivation, which results in shorter life expectancy. A person who inherits the sickle cell gene from one parent and a normal hemoglobin allele (HgbA) from the other, has a normal life expectancy. However, these heterozygote individuals, known as carriers of the sickle cell trait, may suffer problems from time to time.

The heterozygote is resistant to the malarial parasite which kills a large number of people each year. This is an example of balancing selection between the fierce selection against homozygous sickle-cell sufferers, and the selection against the standard HgbA homozygotes by malaria. The heterozygote has a permanent advantage (a higher fitness) wherever malaria exists.[5][6] Maintenance of the HgbS allele through positive selection is supported by significant evidence that heterozygotes have decreased fitness in regions where malaria is not prevalent. In Surinam, for example, the allele is maintained in the gene pools of descendants of African slaves, as the Surinam suffers from perennial malaria outbreaks. Curacao, however, which also has a significant population of individuals descending from African slaves, lacks the presence of widespread malaria, and therefore also lacks the selective pressure to maintain the HgbS allele. In Curacao, the HgbS allele has decreased in frequency over the past 300 years, and will eventually be lost from the gene pool due to heterozygote disadvantage.[7]

Frequency-dependent selection

[edit]
Main article: Frequency-dependent selection

Frequency-dependent selection occurs when the fitness of a phenotype is dependent on its frequency relative to other phenotypes in a given population. In positive frequency-dependent selection the fitness of a phenotype increases as it becomes more common. In negative frequency-dependent selection the fitness of a phenotype decreases as it becomes more common. For example, in prey switching, rare morphs of prey are actually fitter due to predators concentrating on the more frequent morphs. As predation drives the demographic frequencies of the common morph of prey down, the once rare morph of prey becomes the more common morph. Thus, the morph of advantage now is the morph of disadvantage. This may lead to boom and bust cycles of prey morphs. Host-parasite interactions may also drive negative frequency-dependent selection, in alignment with the Red Queen hypothesis. For example, parasitism of freshwater New Zealand snail (Potamopyrgus antipodarum) by the trematode Microphallus sp. results in decreasing frequencies of the most commonly hosted genotypes across several generations. The more common a genotype became in a generation, the more vulnerable to parasitism by Microphallus sp. it became.[8] Note that in these examples that no one phenotypic morph, nor one genotype is entirely extinguished from a population, nor is one phenotypic morph nor genotype selected for fixation. Thus, polymorphism is maintained by negative frequency-dependent selection.

Fitness varies in time and space

[edit]

The fitness of a genotype may vary greatly between larval and adult stages, or between parts of a habitat range.[9] Variation over time, unlike variation over space, is not in itself enough to maintain multiple types, because in general the type with the highest geometric mean fitness will take over, but there are a number of mechanisms that make stable coexistence possible.[10]

More complex examples

[edit]

Species in their natural habitat are often far more complex than the typical textbook examples.

Grove snail

[edit]

The grove snail, Cepaea nemoralis, is famous for the rich polymorphism of its shell. The system is controlled by a series of multiple alleles. Unbanded is the top dominant trait, and the forms of banding are controlled by modifier genes (see epistasis).

Grove snail, dark yellow shell with single band

In England the snail is regularly preyed upon by the song thrush Turdus philomelos, which breaks them open on thrush anvils (large stones). Here fragments accumulate, permitting researchers to analyse the snails taken. The thrushes hunt by sight, and capture selectively those forms which match the habitat least well. Snail colonies are found in woodland, hedgerows and grassland, and the predation determines the proportion of phenotypes (morphs) found in each colony.

Two active grove snails

A second kind of selection also operates on the snail, whereby certain heterozygotes have a physiological advantage over the homozygotes. Thirdly, apostatic selection is likely, with the birds preferentially taking the most common morph. This is the 'search pattern' effect, where a predominantly visual predator persists in targeting the morph which gave a good result, even though other morphs are available.

The polymorphism survives in almost all habitats, though the proportions of morphs varies considerably. The alleles controlling the polymorphism form a supergene with linkage so close as to be nearly absolute. This control saves the population from a high proportion of undesirable recombinants.

In this species predation by birds appears to be the main (but not the only) selective force driving the polymorphism. The snails live on heterogeneous backgrounds, and thrush are adept at detecting poor matches. The inheritance of physiological and cryptic diversity is preserved also by heterozygous advantage in the supergene.[11][12][13][14][15] Recent work has included the effect of shell colour on thermoregulation,[16] and a wider selection of possible genetic influences is also considered.[17]

Chromosome polymorphism in Drosophila

[edit]

In the 1930s Theodosius Dobzhansky and his co-workers collected Drosophila pseudoobscura and D. persimilis from wild populations in California and neighbouring states. Using Painter's technique,[18] they studied the polytene chromosomes and discovered that all the wild populations were polymorphic for chromosomal inversions. All the flies look alike whatever inversions they carry, so this is an example of a cryptic polymorphism. Evidence accumulated to show that natural selection was responsible:

Drosophila polytene chromosome
  1. Values for heterozygote inversions of the third chromosome were often much higher than they should be under the null assumption: if no advantage for any form the number of heterozygotes should conform to Ns (number in sample) = p2+2pq+q2 where 2pq is the number of heterozygotes (see Hardy–Weinberg equilibrium).
  2. Using a method invented by L'Heretier and Teissier, Dobzhansky bred populations in population cages, which enabled feeding, breeding and sampling whilst preventing escape. This had the benefit of eliminating migration as a possible explanation of the results. Stocks containing inversions at a known initial frequency can be maintained in controlled conditions. It was found that the various chromosome types do not fluctuate at random, as they would if selectively neutral, but adjust to certain frequencies at which they become stabilised.
  3. Different proportions of chromosome morphs were found in different areas. There is, for example, a polymorph-ratio cline in D. robusta along an 18-mile (29 km) transect near Gatlinburg, TN passing from 1,000 feet (300 m) to 4,000 feet.[19] Also, the same areas sampled at different times of year yielded significant differences in the proportions of forms. This indicates a regular cycle of changes which adjust the population to the seasonal conditions. For these results selection is by far the most likely explanation.
  4. Lastly, morphs cannot be maintained at the high levels found simply by mutation, nor is drift a possible explanation when population numbers are high.

By 1951 Dobzhansky was persuaded that the chromosome morphs were being maintained in the population by the selective advantage of the heterozygotes, as with most polymorphisms.[20][21][22]

See also

[edit]

References

[edit]
Revisions and contributorsEdit on WikipediaRead on Wikipedia

Balancing selection

View on Grokipedia
from Grokipedia
Balancing selection is a mode of in that actively maintains genetic polymorphism within populations by counteracting the loss of allelic variation due to or , thereby preserving multiple at a locus over extended periods. The concept was first proposed by in the 1940s through his balance hypothesis and gained empirical support from Lewontin and Hubby's 1966 studies on allozyme variation. Unlike , which favors one leading to fixation, balancing selection promotes an equilibrium where intermediate allele frequencies are sustained, enhancing overall and adaptability. This process is particularly evident in traits under complex environmental pressures, such as disease resistance, where it contributes to phenotypic variation across . Key mechanisms of balancing selection include (overdominance), where individuals carrying two different s at a locus exhibit higher fitness than homozygotes; frequency-dependent selection, in which the fitness of an decreases as its frequency increases, favoring rare variants; and spatially or temporally fluctuating selection, where different alleles are advantageous in varying environments or over time. These mechanisms ensure that no single allele dominates, resulting in elevated nucleotide diversity (π) and deviations from neutral expectations in genomic data. Balancing selection is detected through statistical tests like , which identifies excess intermediate-frequency variants, or composite likelihood ratio tests that scan for signatures of long-term polymorphism. Notable examples illustrate its role across taxa: in humans, the sickle-cell allele (HBB gene) persists due to heterozygote resistance to malaria, while (MHC) loci maintain diversity for immune response via against pathogens. In plants, self-incompatibility loci evolve under balancing selection to prevent , and in crustaceans like , trans-species polymorphisms at resistance genes against parasites like Pasteuria ramosa reflect millions of years of coevolutionary pressure. Overall, balancing selection underscores the evolutionary importance of , influencing , , and resilience to environmental changes.

Introduction

Definition

Balancing selection is a form of that actively maintains within populations by favoring multiple s at a locus, resulting in stable polymorphisms where frequencies equilibrate at intermediate levels higher than those expected under alone. This process counteracts the effects of purifying selection, which eliminates deleterious variants and reduces variation, and , which drives the fixation of advantageous s and erodes diversity. Instead, balancing selection preserves variation by equalizing fitness differences among genotypes, preventing any single from dominating. In a simple two-allele model under balancing selection, such as one involving (overdominance), the equilibrium frequency p^\hat{p} of allele A is given by p^=ts+t,\hat{p} = \frac{t}{s + t}, where ss is the selection coefficient against the AA homozygote and tt is the selection coefficient against the aa homozygote, assuming the heterozygote Aa has the highest fitness. This equilibrium arises because the relative fitnesses create opposing selective pressures that stabilize allele frequencies, ensuring neither allele is lost to drift or fixation. The evolutionary outcomes of balancing selection include the persistence of , where heterozygotes outperform homozygotes; negative , where rare alleles gain a fitness advantage; and to heterogeneous environments, all of which sustain genetic polymorphisms over time. One common mechanism, such as , exemplifies how balancing selection promotes diversity by conferring superior fitness to mixed genotypes.

Historical Development

The concept of balancing selection emerged in the early as researchers observed persistent genetic polymorphisms that challenged the prevailing view of as primarily driven by gradual, directional changes. In 1937, highlighted chromosomal polymorphisms in Drosophila species, interpreting them as evidence against strict Darwinian and suggesting mechanisms that maintain within populations. During the 1940s and , Dobzhansky and collaborators integrated balancing selection into the modern evolutionary synthesis, which synthesized Mendelian genetics, , and ; this framework contrasted with J.B.S. Haldane's earlier emphasis on in models from the 1920s and 1930s. Key figures advanced empirical support: Dobzhansky continued documenting inversion polymorphisms in as outcomes of balancing forces; E.B. Ford, through studies in the on shell color polymorphisms in snails, demonstrated how environmental pressures could sustain multiple alleles via selective maintenance. Bruce Wallace's experiments in the on irradiated populations provided direct evidence of heterozygote superiority, where hybrid individuals exhibited higher fitness than homozygotes, reinforcing balancing selection's role in polymorphism persistence. The 1970s marked a shift toward explicit modeling of frequency-dependent dynamics within balancing selection, with Francisco J. Ayala's work on showing how rare genotypes gain fitness advantages, stabilizing polymorphisms through negative frequency dependence. In the 1980s and 1990s, genomic analyses of (MHC) loci in humans and other vertebrates revealed excess allelic diversity and trans-species polymorphisms, providing molecular signatures of long-term balancing selection against pathogen-driven pressures. The 1960s neutralist-selectionist controversy introduced skepticism toward balancing selection, as Motoo Kimura's neutral theory (1968) proposed that much genetic variation arose from drift rather than selection, challenging the selectionist paradigm that relied on balancing mechanisms to explain observed polymorphisms. This debate was largely resolved in the 1980s and 1990s by molecular data, including MHC studies and allozyme surveys, which detected non-neutral patterns like elevated heterozygosity and consistent with balancing selection.

Core Mechanisms

Heterozygote Advantage

, also known as , is a key mechanism of balancing selection where individuals heterozygous for a particular genetic locus exhibit higher fitness than either corresponding homozygote. In this , the fitness of the heterozygote Aa surpasses that of both AA and aa, creating selective pressure that favors the maintenance of by counteracting the tendency for advantageous alleles to fix in the population. This process ensures that both alleles persist at intermediate frequencies, promoting polymorphism. The classic theoretical model for heterozygote advantage assigns relative fitness values to the genotypes as follows: AA has fitness 1−s1 - s, Aa has fitness 11, and aa has fitness 1−t1 - t, where s>0s > 0 and t>0t > 0 are selection coefficients quantifying the fitness deficits of the respective homozygotes relative to the heterozygote. Under this model, the population reaches a stable equilibrium allele frequency for the A allele at p^=ts+t\hat{p} = \frac{t}{s + t}, where the selective disadvantages balance out, preventing either allele from being eliminated. This equilibrium is stable only if both s>0s > 0 and t>0t > 0; if the fitness of one homozygote exceeds or equals that of the heterozygote (e.g., if s≤0s \leq 0), the superior allele will fix, and the polymorphism will be lost. The evolutionary implications of are profound, as it actively prevents fixation and sustains , particularly at loci associated with disease resistance where heterozygotes often provide enhanced protection against environmental threats. This mechanism is especially relevant in uniform environments where genotypic fitness differences drive selection independently of frequencies. A well-known application is seen in human populations with the sickle cell , where heterozygotes gain resistance. To understand how this equilibrium arises, consider the derivation using Hardy-Weinberg principles under viability selection. Assume initial frequencies pp for A and q=1−pq = 1 - p for a, yielding frequencies p2p^2 for AA, 2pq2pq for Aa, and q2q^2 for aa before selection. After selection, the frequencies become proportional to p2(1−s)p^2 (1 - s), 2pq⋅12pq \cdot 1, and q2(1−t)q^2 (1 - t), with mean population fitness wˉ=1−sp2−tq2\bar{w} = 1 - s p^2 - t q^2. The updated frequency of A is then p′=p2(1−s)+pqwˉp' = \frac{p^2 (1 - s) + pq}{\bar{w}}. The change in is Δp=p′−p=pq(tq−sp)1−sp2−tq2\Delta p = p' - p = \frac{p q (t q - s p)}{1 - s p^2 - t q^2}, which equals zero when p=p^=ts+tp = \hat{p} = \frac{t}{s + t}, confirming stability as deviations from equilibrium result in directional changes toward it (Δp>0\Delta p > 0 if p<p^p < \hat{p}, and Δp<0\Delta p < 0 if p>p^p > \hat{p}). This derivation illustrates how generates a restorative force on frequencies.

Frequency-Dependent Selection

Frequency-dependent selection is a form of in which the fitness of a , , or varies depending on its relative frequency within the . This process can be classified into two primary types: negative frequency-dependent selection, where the fitness of a variant declines as it becomes more common, thereby favoring rarer variants; and positive frequency-dependent selection, where fitness increases with rising frequency, often promoting the spread of the most common variant toward fixation. Negative frequency-dependent selection serves as a key balancing mechanism by stabilizing multiple alleles at intermediate frequencies, preventing the loss of through the enhanced relative fitness of less common types. In contrast, positive frequency-dependent selection typically erodes polymorphism by accelerating the dominance of prevalent alleles. The balancing role of negative arises through ecological interactions where rarity confers an advantage, such as in predator-prey dynamics or competitive resource use. For instance, apostatic selection occurs when visual predators disproportionately attack common prey morphs due to search image formation, allowing rarer morphs to experience lower predation rates and persist in the population. Experiments with wild birds foraging on artificial polymorphic prey have confirmed this mechanism, showing that attack rates on specific morphs decrease as their frequency rises, thus maintaining color polymorphism. Similarly, in resource competition scenarios, rare genotypes can more effectively exploit underutilized niches or resources, as demonstrated in experimental populations of where frequency-dependent fitness advantages preserved variation between sexual and asexual reproductive strategies. These processes ensure that no single variant dominates, as its increasing abundance diminishes its relative success. Mathematically, negative frequency-dependent selection can be modeled by assigning fitness that inversely scales with its own . A basic formulation gives the fitness of A as wA=1−spw_A = 1 - s p, where s>0s > 0 represents the strength of selection and pp is the of A (with a symmetric form for the alternative ). Under this model, an equilibrium is reached when the marginal fitness of the rarer matches that of the common one, typically at p=0.5p = 0.5 for symmetric parameters, where both alleles have equal fitness. This setup illustrates how increasing erodes an 's advantage, stabilizing polymorphism. Stability in such systems depends on the marginal fitness of alleles declining monotonically with their , which ensures that deviations from equilibrium are corrected. In more complex analyses using the pairwise interaction model, equilibria under negative frequency-dependence are often and maintain full polymorphism across multiple alleles, with simulations revealing that this occurs more frequently than under constant selection regimes—for example, over 60 times more often for five alleles. Conversely, positive frequency-dependence in these simulations frequently results in fixation of one allele or transient cycles before loss of diversity, highlighting its disruptive potential. Although distinct from mechanisms like , frequency-dependent effects can interact with genotypic superiorities in hybrid models to reinforce polymorphism maintenance.

Spatiotemporal Variation in Fitness

Spatiotemporal variation in fitness represents a key mechanism of balancing selection, where environmental heterogeneity across or time imposes differing selective pressures on alleles, preventing any single variant from achieving fixation and thereby sustaining genetic polymorphism within populations. In spatial variation, alleles may confer advantages in distinct habitats, with through migration counteracting local to maintain diversity at the metapopulation level. This process requires sufficient dispersal rates to mix alleles without eroding local differences entirely. A foundational theoretical framework for spatial variation is provided by Levene's model, which demonstrates how polymorphism can be stably maintained when selection favors different s in multiple ecological niches connected by migration. In this model, the fitness of a is calculated as the weighted sum across niches: wˉ=∑miwi\bar{w} = \sum m_i w_i, where mim_i denotes the proportion of the migrating to or residing in niche ii, and wiw_i is the fitness of the in that niche. Stable polymorphism arises if the niche-specific fitness differ sufficiently, such that no has the highest weighted fitness across all environments. This setup predicts clinal variation in frequencies along environmental gradients, reflecting a balance between localized selection and . Temporal variation in fitness occurs in fluctuating environments, such as those driven by seasonal changes or unpredictable cycles, where no consistently outperforms others over multiple generations. Here, selection pressures alternate, favoring different alleles at different times, which can protect polymorphism if the long-term growth rate of each remains positive. Theoretical models emphasize the fitness over generations as the critical metric: an persists if its fitness exceeds unity, even amid yearly fluctuations where arithmetic means may vary. This condition holds under discrete generations without overlapping, though overlapping generations can modify the dynamics by smoothing extreme fluctuations. Such temporal heterogeneity often leads to cyclic fluctuations in allele frequencies synchronized with environmental changes.

Natural Examples

Sickle Cell Anemia in Humans

Sickle cell anemia exemplifies balancing selection through in humans, where the HbS allele provides protection against at the cost of disease in homozygotes. The HbS allele arises from a single in the beta-globin gene (HBB) on 11p15.5, substituting for and resulting in replacing at the sixth position of the beta-globin protein. Individuals homozygous for the mutant allele (SS genotype) develop , an autosomal recessive disorder characterized by abnormal polymerization under low-oxygen conditions, leading to red blood cell sickling, chronic , vaso-occlusive crises, and increased susceptibility to infections. In contrast, heterozygotes (AS genotype, or ) experience minimal symptoms under normal conditions but exhibit resistance to severe infection by the parasite Plasmodium falciparum, as the altered s inhibit parasite growth and survival. The geographic distribution of the HbS closely mirrors historical malaria endemicity, with elevated frequencies maintained by balancing selection in affected regions. In and parts of the , where P. falciparum malaria has been hyperendemic, the AS reaches 10-20% (HbS of approximately 0.05-0.10), particularly among populations like those in West and . This pattern extends to and the , aligning with areas of intense malaria transmission over millennia. Where malaria control measures, such as insecticide-treated nets and antimalarial drugs, have reduced parasite , HbS frequencies have begun to decline, as the selective advantage for heterozygotes diminishes. Pioneering evidence for this polymorphism's adaptive role came from A.C. Allison's 1954 study in , which demonstrated lower malaria parasitemia and infection rates among AS individuals compared to AA homozygotes, suggesting heterozygote protection as the mechanism balancing the deleterious SS genotype. Subsequent clinical and epidemiological data confirmed that AS carriers have 50-90% reduced risk of severe complications, including cerebral malaria and severe anemia. Modern genome-wide association studies (GWAS) have further validated this resistance, identifying the HBB locus as a key signal of selection and elucidating mechanisms like enhanced parasite clearance in AS erythrocytes. In malaria-endemic areas, relative fitness estimates illustrate the balancing dynamics: AA homozygotes have fitness around 0.9 due to malaria mortality, AS heterozygotes approximate 1.0 with their protective advantage, and SS homozygotes around 0.2 owing to severity. This leads to a stable equilibrium p^≈0.1\hat{p} \approx 0.1, calculated as the ratio of selection against AA to total selection against both homozygotes, maintaining polymorphism despite the SS burden. Following post-colonial migrations, such as those of African populations to non-malarial regions like the , balancing selection relaxes; the HbS frequency in has declined from an ancestral ~0.1 to ~0.04 today, driven by European admixture (20-30%) and ongoing selection against SS without counterbalancing pressure.

Grove Snail Polymorphism

The grove snail () displays a prominent shell polymorphism that exemplifies balancing selection through frequency-dependent and spatially varying mechanisms. This variation primarily involves shell ground colors of , , or , combined with banding patterns (either present or absent), yielding five main morphs: yellow unbanded, yellow banded, brown unbanded, brown banded, and an intermediate form often classified with banding. These phenotypes are genetically controlled by multiple loci, including a primary locus for ground color (with brown dominant over pink and yellow alleles) and separate loci for banding suppression or modification. A primary selective force maintaining this diversity is predation by song thrushes (Turdus philomelos), which preferentially consume conspicuous snails, thereby favoring cryptic morphs that blend with local backgrounds. For example, yellow morphs are advantageous in open grasslands where they match pale vegetation, while brown morphs provide better in wooded or shaded . Seminal studies by and Sheppard in the provided key evidence for these dynamics, revealing that morph frequencies in populations closely correspond to types, with yellow shells dominating in grasslands and brown in denser woodlands. These investigations also uncovered apostatic predation, a form of negative , wherein thrushes disproportionately target the most abundant morphs in a given area, thus stabilizing local diversity. The polymorphism persists due to negative frequency-dependence operating within sites, which curbs the rise of any single morph, alongside broader in selection across habitats that sustains overall . Surveys conducted in the 2000s have affirmed the endurance of these patterns amid and climate shifts, with molecular analyses indicating that between populations hinders local fixation and reinforces polymorphism.

Drosophila Chromosome Inversions

Chromosome inversions in Drosophila species, particularly paracentric inversions on the second and third chromosomes, serve as classic examples of balancing selection by suppressing recombination in heterozygotes, thereby preserving co-adapted allele blocks that enhance fitness in heterogeneous environments. In Drosophila pseudoobscura, third-chromosome inversions, such as the Standard and Arrowhead arrangements, exemplify this structure, encompassing multiple loci that are maintained as a unit due to reduced crossing over, which links favorable allele combinations and prevents their disruption by standard arrangements. This suppression of recombination allows inversions to act as supergenes, capturing sets of alleles adapted to specific ecological pressures, such as varying climates or seasonal fluctuations. The selective maintenance of these inversions often involves , where individuals carrying one inverted and one standard chromosome exhibit superior performance in diverse habitats compared to homozygotes. In D. pseudoobscura, inversion frequencies form stable latitudinal clines, increasing toward higher latitudes in , reflecting adaptation to cooler, more variable conditions. Pioneering surveys by in the 1940s documented these clines across populations from to , revealing persistent polymorphisms that could not be explained by alone. Homozygotes for inversions show reduced fitness, often due to accumulated recessive deleterious mutations or disrupted co-adaptation, leading to lower viability and contributing to the balanced state. Balancing selection in these systems operates through spatiotemporal variation in fitness, as differing climates along gradients favor distinct inversion arrangements in heterozygotes, and negative , where rarer inversions gain an advantage in heterogeneous populations by complementing common types. For instance, seasonal shifts in Drosophila melanogaster inversions like In(2L)t correlate with temperature extremes, maintaining polymorphism via temporally varying selection. Genomic sequencing efforts in the have illuminated the adaptive alleles within these inversions, identifying genes involved in temperature tolerance and stress response that underlie clinal variation. In D. pseudoobscura, whole-genome analyses revealed that third-chromosome inversions harbor loci associated with acclimation and metabolic efficiency, supporting its role in local adaptation while preserving overall polymorphism through balancing forces. These insights confirm that inversions facilitate rapid evolutionary responses to environmental heterogeneity without losing .

Theoretical and Empirical Insights

Mathematical Models

Mathematical models of balancing selection provide theoretical frameworks to predict dynamics and polymorphism maintenance under various selective regimes. A foundational approach is the general viability selection model for multiple alleles at a single locus, where the recursion for allele frequencies p′\mathbf{p}' in the next generation is given by p′=p∘(Wp)pTWp,\mathbf{p}' = \frac{\mathbf{p} \circ (\mathbf{W} \mathbf{p})}{\mathbf{p}^T \mathbf{W} \mathbf{p}}, with p\mathbf{p} as the vector of current frequencies, W\mathbf{W} the symmetric fitness matrix specifying genotypic viabilities, ∘\circ the Hadamard (element-wise) product. This deterministic model assumes infinite and random mating, yielding mean fitness wˉ=pTWp\bar{w} = \mathbf{p}^T \mathbf{W} \mathbf{p} as the normalizing denominator. Under balancing selection, such as multi-allelic where heterozygote fitnesses exceed homozygote fitnesses (i.e., off-diagonal elements of W\mathbf{W} surpass diagonal elements), stable interior equilibria exist at frequencies p^\hat{\mathbf{p}} satisfying Wp^=λp^\mathbf{W} \hat{\mathbf{p}} = \lambda \hat{\mathbf{p}} for eigenvalue λ=wˉ\lambda = \bar{w}, provided the leading eigenvalue is positive and the matrix structure ensures global stability via properties. Unified theoretical approaches integrate multiple balancing mechanisms into cohesive frameworks. Gillespie's 1977 temporal fluctuation model incorporates environmental variability by assuming genotypic fitnesses fluctuate randomly over generations, favoring genotypes with lower variance in offspring numbers ( fitness maximization); this leads to protected polymorphism when fluctuations correlate with allelic effects, maintaining multiple despite drift in finite settings. Similarly, Karlin's frequency-dependent frameworks from the 1970s model selection coefficients as functions of , such as in symmetric viability schemes where fitnesses decrease with increasing frequency of the favored ; these yield stable equilibria for multi-allelic systems under weak selection, unifying and negative frequency dependence through perturbation analyses around neutrality. Agent-based (or individual-based) simulations extend these models by incorporating stochasticity, finite population sizes, and combined mechanisms to demonstrate polymorphism persistence. For instance, simulations combining with migration in subdivided populations show that between demes with opposing selection pressures stabilizes intermediate frequencies, preventing fixation and yielding higher polymorphism levels than single-mechanism scenarios; this is evident in models where migration rates balance local , resulting in spatially varying but globally maintained diversity. Comparisons with neutral models highlight balancing selection's distinctive signatures. Under neutrality, statistic approximates zero, but balancing selection elevates it positively (D > 0) due to excess intermediate-frequency alleles, contrasting purifying selection's negative values; this predictive power allows forecasting equilibrium frequencies from fitness matrices, where observed spectra match model expectations under or frequency dependence. These models assume infinite populations, neglecting drift's erosion of polymorphism; extensions via diffusion approximations address this by deriving Fokker-Planck equations for processes in finite populations (effective size N_e), revealing that strong balancing selection (selection coefficient s >> 1/N_e) sustains polymorphisms over longer timescales than weak cases, with fixation probabilities approaching zero for protected alleles.

Detection and Evidence in Populations

Balancing selection can be detected through various tests that identify deviations from neutral expectations in genomic data. One key signature is elevated diversity or heterozygosity at loci under balancing selection, as the maintenance of multiple alleles increases polymorphism levels compared to neutrally evolving regions. Similarly, of the site frequency spectrum (SFS), such as , often show positive values under balancing selection due to an excess of intermediate-frequency variants, contrasting with the rare-allele skew seen under purifying selection or recent positive selection. Fu's Fs statistic can also yield positive values in these cases, reflecting reduced numbers of rare alleles and supporting the inference of balancing over neutrality. Patterns in (LD) provide additional evidence, particularly for ancient or ongoing balancing selection, where extended at carrying the selected may surround selected loci due to the persistence of divergent over time. Although integrated haplotype score (iHS) tests were originally designed for detecting recent positive selection via LD decay, they can sometimes capture balancing signatures when frequencies are stably intermediate, though such signals may mimic incomplete lineage sorting or demographic effects. These LD-based approaches are most effective when combined with SFS statistics to confirm non-neutral patterns. Empirical evidence of balancing selection is prominent in immune-related genes, such as human (MHC) class II loci, where trans-species polymorphisms indicate ancient balancing pressures predating the human-chimpanzee divergence approximately 6-7 million years ago. In , self- (SI) loci, like the S-locus in lyrata, exhibit elevated diversity and reduced recombination, hallmarks of long-term balancing selection that maintains allelic diversity to prevent self-fertilization. Detecting these signatures faces challenges, including confounding effects from population demography, such as bottlenecks or admixture, which can mimic elevated diversity or skewed SFS independently of selection. To address this, Bayesian inference methods like approximate Bayesian computation (ABC) integrate genomic data with demographic models to probabilistically distinguish selection from neutral processes. Recent advances in the have leveraged for more robust genome-wide scans, with deep neural networks trained on simulated SFS and LD patterns outperforming traditional statistics in classifying loci under recent balancing selection while accounting for demographic noise. These methods, sometimes incorporating frameworks to evaluate trait-associated variants, enhance power for detecting subtle, polygenic balancing effects across diverse populations.

References

  1. https://www.cell.com/current-biology/fulltext/S0960-9822(07)00813-5
  2. https://www.nature.com/articles/s41467-024-49726-8
  3. https://pmc.ncbi.nlm.nih.gov/articles/PMC10063222/
  4. https://pmc.ncbi.nlm.nih.gov/articles/PMC3886833/
  5. https://courses.washington.edu/gs562/lectures/lec6.pdf
  6. https://academic.oup.com/mbe/article/26/12/2755/1533368
  7. https://nph.onlinelibrary.wiley.com/doi/10.1111/nph.12441
  8. https://evolution.berkeley.edu/the-history-of-evolutionary-thought/1900-to-present/starting-the-modern-synthesis-theodosius-dobzhansky/
  9. https://digitalcommons.rockefeller.edu/ru-authors/37/
  10. https://www.scielo.br/j/gmb/a/bGnPtyv3QLxjgKsmK4QQcSd/?lang=en
  11. https://academic.oup.com/book/40842/chapter/348870153
  12. https://www.jstor.org/stable/75456
  13. https://www.pnas.org/doi/pdf/10.1073/pnas.44.6.565
  14. https://pmc.ncbi.nlm.nih.gov/articles/PMC1513187/
  15. https://academic.oup.com/gbe/article/16/2/evae003/7600036
  16. https://pmc.ncbi.nlm.nih.gov/articles/PMC4140648/
  17. https://pmc.ncbi.nlm.nih.gov/articles/PMC9132207/
  18. http://courses.washington.edu/gs453/lectures/lec6.pdf
  19. https://pmc.ncbi.nlm.nih.gov/articles/PMC1762409/
  20. https://pmc.ncbi.nlm.nih.gov/articles/PMC3251125/
  21. https://pmc.ncbi.nlm.nih.gov/articles/PMC1931533/
  22. https://bmcecol.biomedcentral.com/articles/10.1186/1472-6785-9-12
  23. https://onlinelibrary.wiley.com/doi/10.1111/j.1558-5646.1984.tb00263.x
  24. https://www.sciencedirect.com/science/article/pii/S0960982215014177
  25. https://pmc.ncbi.nlm.nih.gov/articles/PMC3989104/
  26. https://www.ias.ac.in/article/fulltext/jgen/058/02/0237-0242
  27. https://www.pnas.org/doi/10.1073/pnas.1702994114
  28. https://www.ncbi.nlm.nih.gov/books/NBK22238/
  29. https://medlineplus.gov/genetics/gene/hbb/
  30. https://pmc.ncbi.nlm.nih.gov/articles/PMC3499995/
  31. https://www.nature.com/articles/s41586-021-04288-3
  32. https://pmc.ncbi.nlm.nih.gov/articles/PMC3060623/
  33. https://www.sciencedirect.com/science/article/pii/S014067361261229X
  34. https://www.nature.com/articles/s41598-024-66289-2
  35. https://pmc.ncbi.nlm.nih.gov/articles/PMC2093356/
  36. https://www.sciencedirect.com/science/article/pii/S0006497120473197
  37. https://link.springer.com/article/10.1007/s00439-020-02142-6
  38. https://academic.oup.com/hmg/article/30/R1/R119/6103809
  39. https://www.mun.ca/biology/scarr/Bio4250_Estimates_of_Selection_Coefficients.html
  40. https://pmc.ncbi.nlm.nih.gov/articles/PMC3116635/
  41. https://pmc.ncbi.nlm.nih.gov/articles/PMC4185117/
  42. https://www.nature.com/articles/hdy201274
  43. https://academic.oup.com/biolinnean/article/108/3/484/2415578/Selection-and-disequilibrium-in-Cepaea-nemoralis
  44. https://academic.oup.com/mollus/article/74/3/239/1020723
  45. https://royalsocietypublishing.org/doi/10.1098/rstb.1988.0061
  46. https://academic.oup.com/biolinnean/article/108/3/473/2415589
  47. https://royalsocietypublishing.org/doi/10.1098/rspb.2000.1156
  48. https://www.pnas.org/doi/10.1073/pnas.1432900100
  49. https://www.nature.com/articles/s41437-025-00780-y
  50. https://pubmed.ncbi.nlm.nih.gov/17246159/
  51. https://academic.oup.com/mbe/article/33/5/1317/2579921
  52. https://pubmed.ncbi.nlm.nih.gov/2687095/
  53. https://academic.oup.com/genetics/article/226/2/iyad207/7459204
  54. https://pmc.ncbi.nlm.nih.gov/articles/PMC6179442/
  55. https://www.zoology.ubc.ca/~otto/PopGen500/Lecture2/Overheads.html
  56. https://www.zoology.ubc.ca/let/pdfs/KarlinMcGregor1972.pdf
  57. https://onlinelibrary.wiley.com/doi/10.1111/mec.13226
  58. https://www.pnas.org/doi/10.1073/pnas.162046399
  59. https://www.nature.com/articles/s41598-023-35312-3
  60. https://www.sciencedirect.com/science/article/pii/S0960982205010213
  61. https://journals.plos.org/plosgenetics/article?id=10.1371/journal.pgen.1003011
  62. https://www.liebertpub.com/doi/10.1089/cmb.2021.0447
Add your contribution
Related Hubs
Contribute something
User Avatar
No comments yet.