Community hub
0 subscribers8 pages, 0 posts
Recent from talks
Be the first to start a discussion here.
Be the first to start a discussion here.
Be the first to start a discussion here.
Be the first to start a discussion here.
Contribute something
Welcome to the community hub built to collect knowledge and have discussions related to Reflection mapping.
Nothing was collected or created yet.
Reflection mapping
View on Wikipediafrom Wikipedia
In computer graphics, reflection mapping or environment mapping[1][2][3] is an efficient image-based lighting technique for approximating the appearance of a reflective surface by means of a precomputed texture. The texture is used to store the image of the distant environment surrounding the rendered object.
Several ways of storing the surrounding environment have been employed. The first technique was sphere mapping, in which a single texture contains the image of the surroundings as reflected on a spherical mirror. It has been almost entirely surpassed by cube mapping, in which the environment is projected onto the six faces of a cube and stored as six square textures or unfolded into six square regions of a single texture. Other projections that have some superior mathematical or computational properties include the paraboloid mapping, the pyramid mapping, the octahedron mapping, and the HEALPix mapping.
Reflection mapping is one of several approaches to reflection rendering, alongside e.g. screen space reflections or ray tracing which computes the exact reflection by tracing a ray of light and following its optical path. The reflection color used in the shading computation at a pixel is determined by calculating the reflection vector at the point on the object and mapping it to the texel in the environment map. This technique often produces results that are superficially similar to those generated by raytracing, but is less computationally expensive since the radiance value of the reflection comes from calculating the angles of incidence and reflection, followed by a texture lookup, rather than followed by tracing a ray against the scene geometry and computing the radiance of the ray, simplifying the GPU workload.
However, in most circumstances a mapped reflection is only an approximation of the real reflection. Environment mapping relies on two assumptions that are seldom satisfied:
- All radiance incident upon the object being shaded comes from an infinite distance. When this is not the case the reflection of nearby geometry appears in the wrong place on the reflected object. When this is the case, no parallax is seen in the reflection.
- The object being shaded is convex, such that it contains no self-interreflections. When this is not the case the object does not appear in the reflection; only the environment does.
Environment mapping is generally the fastest method of rendering a reflective surface. To further increase the speed of rendering, the renderer may calculate the position of the reflected ray at each vertex. Then, the position is interpolated across polygons to which the vertex is attached. This eliminates the need for recalculating every pixel's reflection direction.
If normal mapping is used, each polygon has many face normals (the direction a given point on a polygon is facing), which can be used in tandem with an environment map to produce a more realistic reflection. In this case, the angle of reflection at a given point on a polygon will take the normal map into consideration. This technique is used to make an otherwise flat surface appear textured, for example corrugated metal, or brushed aluminium.
Types
[edit]Sphere mapping
[edit]Sphere mapping represents the sphere of incident illumination as though it were seen in the reflection of a reflective sphere through an orthographic camera. The texture image can be created by approximating this ideal setup, or using a fisheye lens or via prerendering a scene with a spherical mapping.
The spherical mapping suffers from limitations that detract from the realism of resulting renderings. Because spherical maps are stored as azimuthal projections of the environments they represent, an abrupt point of singularity (a "black hole" effect) is visible in the reflection on the object where texel colors at or near the edge of the map are distorted due to inadequate resolution to represent the points accurately. The spherical mapping also wastes pixels that are in the square but not in the sphere.
The artifacts of the spherical mapping are so severe that it is effective only for viewpoints near that of the virtual orthographic camera.
Cube mapping
[edit]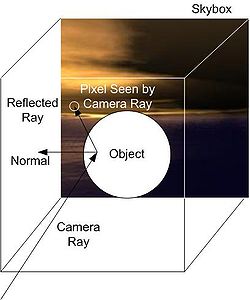
Cube mapping and other polyhedron mappings address the severe distortion of sphere maps. If cube maps are made and filtered correctly, they have no visible seams, and can be used independent of the viewpoint of the often-virtual camera acquiring the map. Cube and other polyhedron maps have since superseded sphere maps in most computer graphics applications, with the exception of acquiring image-based lighting. Image-based lighting can be done with parallax-corrected cube maps.[4]
Generally, cube mapping uses the same skybox that is used in outdoor renderings. Cube-mapped reflection is done by determining the vector that the object is being viewed at. This camera ray is reflected about the surface normal of where the camera vector intersects the object. This results in the reflected ray which is then passed to the cube map to get the texel which provides the radiance value used in the lighting calculation. This creates the effect that the object is reflective.
HEALPix mapping
[edit]HEALPix environment mapping is similar to the other polyhedron mappings, but can be hierarchical, thus providing a unified framework for generating polyhedra that better approximate the sphere. This allows lower distortion at the cost of increased computation.[5]
History
[edit]In 1974, Edwin Catmull created an algorithm for "rendering images of bivariate surface patches"[6][7] which worked directly with their mathematical definition. Further refinements were researched and documented by Bui-Tuong Phong in 1975, and later James Blinn and Martin Newell, who developed environment mapping in 1976; these developments which refined Catmull's original algorithms led them to conclude that "these generalizations result in improved techniques for generating patterns and texture".[6][8][9]
Gene Miller experimented with spherical environment mapping in 1982 at MAGI.
Wolfgang Heidrich introduced Paraboloid Mapping in 1998.[10]
Emil Praun introduced Octahedron Mapping in 2003.[11]
Mauro Steigleder introduced Pyramid Mapping in 2005.[12]
Tien-Tsin Wong, et al. introduced the existing HEALPix mapping for rendering in 2006.[5]
See also
[edit]References
[edit]- ^ "Higher Education | Pearson" (PDF).
- ^ "Directory | Computer Science and Engineering" (PDF). web.cse.ohio-state.edu. Retrieved 2025-02-18.
- ^ "Bump and Environment Mapping" (PDF). Archived from the original (PDF) on 2012-01-29.
- ^ "Image-based Lighting approaches and parallax-corrected cubemap". 29 September 2012.
- ^ a b Tien-Tsin Wong, Liang Wan, Chi-Sing Leung, and Ping-Man Lam. Real-time Environment Mapping with Equal Solid-Angle Spherical Quad-Map Archived 2007-10-23 at the Wayback Machine, Shader X4: Lighting & Rendering, Charles River Media, 2006.
- ^ a b Blinn, James F.; Newell, Martin E. (October 1976). "Texture and reflection in computer generated images". Communications of the ACM. 19 (10): 542–547. doi:10.1145/360349.360353. ISSN 0001-0782.
- ^ Catmull, E.A. Computer display of curved surfaces. Proc. Conf. on Comptr. Graphics, Pattern Recognition, and Data Structure, May 1975, pp. 11-17 (IEEE Cat. No. 75CH0981-1C).
- ^ "Computer Graphics". Archived from the original on 2021-02-24. Retrieved 2007-01-09.
- ^ "Reflection Mapping History".
- ^ Heidrich, W., and H.-P. Seidel. "View-Independent Environment Maps". Eurographics Workshop on Graphics Hardware 1998, pp. 39–45.
- ^ Emil Praun and Hugues Hoppe. "Spherical parametrization and remeshing". ACM Transactions on Graphics, 22(3):340–349, 2003.
- ^ Mauro Steigleder. "Pencil Light Transport". A thesis presented to the University of Waterloo, 2005.
External links
[edit]Reflection mapping
View on Grokipediafrom Grokipedia
Reflection mapping, also known as environment mapping, is a computer graphics technique that approximates the appearance of reflective or refractive surfaces by projecting a precomputed image of the surrounding environment onto an object, using reflection vectors derived from surface normals and viewer position to index into the environment map.[1] This method enables efficient simulation of mirror-like reflections without the computational cost of full ray tracing, assuming the environment is distant and static relative to the reflecting object.[1]
The technique was first introduced by James F. Blinn and Martin E. Newell in their 1976 paper "Texture and Reflection in Computer Generated Images," where they described using a 2D intensity map projected onto a sphere to compute reflected light intensities for curved surfaces, providing accurate normals via a subdivision algorithm.[1] Early implementations focused on sphere mapping, which stores the environment as a single texture representing reflections on a spherical mirror, but it suffers from sampling artifacts and inefficient use of texture space due to polar coordinate distortions.[2] A significant advancement came in 1986 with Ned Greene's proposal of cube mapping, which divides the environment into six square images corresponding to the faces of a cube centered at the object, offering more uniform sampling, easier generation, and better support for real-time applications like video games and simulations.[3]
Other variants include dual paraboloid mapping for hemispherical coverage and more recent methods like screen-space reflections for dynamic scenes, though traditional environment mapping excels in interactive rendering by prefiltering the environment for specular highlights and diffuse interreflections. Despite its efficiency, reflection mapping has limitations, such as inability to handle occlusions, self-reflections, or parallax effects accurately, often requiring hybrid approaches with ray tracing for high-fidelity results in modern graphics pipelines.[2]
Fundamentals
Definition and Purpose
Reflection mapping, also known as environment mapping, is a computer graphics technique that simulates the appearance of reflections on glossy or curved surfaces by projecting a precomputed two-dimensional image of the surrounding environment onto the object's surface, using the surface normal and viewer direction to index the appropriate environmental radiance.[4] This method models the incoming light from all directions as if the environment were mapped onto an infinitely large sphere surrounding the object, allowing for the approximation of specular highlights and mirror-like effects without tracing individual light paths.[4] The primary purpose of reflection mapping is to achieve efficient rendering of realistic reflections in real-time applications, such as video games and interactive simulations, by avoiding the high computational cost of exact reflection calculations like ray tracing, which require solving integral equations for light transport across the entire scene.[4][5] Instead, it provides a local approximation that treats the environment as static and distant, enabling fast texture lookups to enhance visual fidelity for materials exhibiting shiny or reflective properties, such as metals, glass, and water surfaces.[4] This approach significantly reduces rendering time while maintaining perceptual realism, making it suitable for hardware-constrained systems.[5] Unlike global illumination techniques, such as ray tracing, which compute accurate light interactions including multiple bounces and inter-object reflections, reflection mapping simplifies the process by ignoring object-environment occlusions and assuming no parallax or motion in the surroundings relative to the reflective surface.[4] Developed in the 1970s to overcome limitations in early computer graphics hardware, it laid the groundwork for subsequent advancements in interactive rendering.[4] One common implementation involves cube mapping, where the environment is captured across six orthogonal faces of a cube for uniform sampling.[6]Basic Principles
Reflection mapping builds upon the foundational concept of texture mapping, which assigns two-dimensional coordinates, often denoted as (u, v), to points on a three-dimensional surface to sample colors or patterns from a pre-defined image, thereby enhancing the visual detail of rendered objects without increasing geometric complexity.[7] In reflection mapping, the "texture" is an environment map—a panoramic representation of the surrounding scene—allowing for the simulation of reflective surfaces by approximating how light from the environment interacts with an object. The core workflow of reflection mapping involves three primary steps. First, an environment map is captured or generated, typically as a 360-degree panoramic image of the surroundings, which can be obtained through photography (such as using a mirrored sphere), rendering a simulated scene, or artistic creation to represent the distant environment.[8] Second, for a given point on the object's surface, the reflection vector is computed, which indicates the direction from which incoming light would appear to reflect toward the viewer based on the local surface normal and viewing direction. Third, this reflection vector is used to sample the environment map, retrieving the color and intensity that correspond to the reflected light, which is then applied to shade the surface point. This process enables efficient per-pixel shading during rendering. The reflection vector embodies an idealized model of perfect specular reflection, adhering to the law of reflection where the incident angle equals the reflection angle relative to the surface normal, though adapted for approximate real-time computation in graphics without tracing actual rays.[8] One early and simple realization of this approach is sphere mapping, which treats the environment as projected onto an imaginary surrounding sphere centered at the object.[8] Reflection mapping operates under key assumptions to maintain computational efficiency: the environment is static, with the object undergoing minimal translation (though rotation is permissible), and reflections are local to the object without accounting for inter-object bounces or global illumination effects.[8] It accommodates various material types—diffuse for scattered light, specular for mirror-like highlights, and glossy for intermediate roughness—by blending contributions from separate precomputed maps for diffuse irradiance and specular reflections, weighted by material properties.[8]Mapping Techniques
Sphere Mapping
Sphere mapping, the foundational technique in reflection mapping, simulates mirror-like reflections by projecting the environment onto the inner surface of a virtual sphere that surrounds the reflecting object. Introduced by Blinn and Newell in 1976, this method models the environment as a distant, static panorama, ignoring effects like parallax or self-shadowing to enable real-time computation. The spherical projection assumes the object is at the sphere's center, allowing reflections to be approximated solely based on surface normals and viewer position.[1] The setup uses a single 2D texture to store the environment, captured in an equirectangular (latitude-longitude) format that unwraps the sphere into a rectangular image, with horizontal coordinates representing azimuth and vertical ones representing elevation. For rendering, the reflection vector at each surface point is normalized and transformed into spherical coordinates—specifically, latitude and longitude values—for direct texture sampling, blending the result with diffuse lighting to produce the final color. This approach is computationally lightweight, requiring only a vector normalization and coordinate conversion per fragment.[1][9] Visually, sphere mapping excels at creating seamless, continuous reflections for far-field scenes, such as skies or large indoor spaces, where the infinite-distance assumption holds. However, it introduces noticeable distortions for nearby geometry, as the uniform spherical projection warps angular relationships, compressing equatorial regions and exaggerating polar areas. The equirectangular texture exacerbates this with singularities at the poles, where infinite stretching occurs, leading to uneven texel distribution and potential aliasing during sampling.[10][9] Compared to later cube mapping, which mitigates these issues through orthogonal planar faces for more isotropic sampling, sphere mapping's simplicity made it ideal for hardware-limited systems but limits its use in scenarios with close-range or anisotropic environments.[11][10]Cube Mapping
Cube mapping, a prominent technique in reflection mapping, involves projecting the surrounding environment onto the six faces of an imaginary cube centered at the reflecting object, creating a 360-degree representation akin to a skybox that captures views in all directions. This approach allows for vector-based sampling, where a reflection or view direction vector is used to query the appropriate cube face and compute the corresponding texture coordinates, enabling accurate simulation of environmental reflections without relying on spherical coordinates. The method was first described in detail by Miller and Hoffman in 1984, who proposed storing reflection maps across six cube faces for efficient lookup in illumination computations.[12] In setup, the cube map is typically constructed from six square textures—either as separate images or arranged in a cross-shaped layout for single-texture binding in graphics APIs like OpenGL—or generated dynamically by rendering the scene from the cube's center toward each face. The reflection vector, computed from the surface normal and incident light or view direction, determines the target face by identifying the axis with the largest absolute component, after which UV coordinates are derived by normalizing the remaining components and mapping them to the [0,1] range on that face. This process, formalized by Greene in 1986 using gnomonic projection for each face, ensures perspective-correct sampling from the cube's interior. Cube maps support dynamic updates, such as rotating the entire map to simulate object movement relative to the environment, which is particularly useful in interactive applications.[13][12] Compared to earlier sphere mapping techniques, cube mapping provides uniform sampling across directions with minimal distortion, as each face uses a linear perspective projection rather than the warping inherent in cylindrical or spherical unwraps, resulting in more accurate reflections especially near edges. For filtering, cube maps employ mipmapping to handle multi-resolution levels for distant or low-detail reflections, combined with bilinear interpolation within each face to smooth transitions and reduce aliasing on glossy surfaces; trilinear filtering extends this by interpolating between mipmap levels for seamless blending. In practice, this technique is widely adopted in modern game engines, such as Unreal Engine, where it facilitates real-time reflections on dynamic objects like vehicles or architectural elements by capturing scene cubemaps on the fly.[14]HEALPix and Other Methods
HEALPix, or Hierarchical Equal Area isoLatitude Pixelization, is a spherical pixelization scheme originally developed for analyzing cosmic microwave background radiation data, where it enables efficient discretization and fast harmonic analysis of spherical datasets. In computer graphics, it has been adapted for environment mapping to provide isotropic sampling of reflection environments, partitioning the sphere into 12 base quadrilateral regions that subdivide hierarchically into equal-area pixels, each spanning identical solid angles for uniform coverage without polar distortion.[15] This setup facilitates high-fidelity reflections in simulations by mapping a 360-degree environment onto a single rectangular texture, supporting mipmapping and compression while preserving visual details comparable to higher-resolution cubemaps, such as using 90×90 pixels per base quad for approximately 97,200 total pixels versus 98,304 for a 128×128 cubemap.[15] Paraboloid mapping employs dual paraboloid projections to cover the full sphere using two hemispherical textures, projecting reflection directions onto paraboloid surfaces centered at the reflection point for efficient environment sampling.[16] Introduced as an alternative to cubic methods, it simplifies rendering by requiring only two texture updates instead of six, reducing memory and computational overhead while enabling vertex-shader implementations for real-time applications.[16] This approach balances quality and performance, though it can introduce minor filtering artifacts at the equator seam between paraboloids. Cylindrical mapping projects the spherical environment onto a cylinder unrolled into a rectangular texture, typically using azimuthal angle for horizontal coordinates and latitude for vertical, making it suitable for panoramic scenes with horizontal dominance.[17] In reflection mapping, it indexes textures based on the reflection vector's cylindrical coordinates, providing a straightforward way to handle 360-degree surroundings like indoor or urban environments, though it suffers from stretching near the poles. HEALPix finds unique applications in astrophysics visualizations, where its equal-area partitioning supports accurate rendering of celestial sphere data, such as star fields or radiation maps, adapted for graphics to simulate isotropic reflections in scientific simulations.[15] Paraboloid mapping is particularly efficient for mobile graphics, enabling real-time soft shadows and reflections on resource-constrained devices through techniques like concentric spherical representations combined with dual paraboloid updates.[18] Cylindrical mapping excels in panoramic scene rendering, commonly used for immersive environments in virtual reality or architectural visualizations.| Method | Pros vs. Sphere/Cube | Cons vs. Sphere/Cube |
|---|---|---|
| HEALPix | Uniform solid-angle sampling reduces distortion for high-fidelity isotropic reflections; single texture simplifies management and supports compression.[15] | More complex shader computation (~20 lines but hierarchical); less hardware acceleration than cubemaps.[15] |
| Paraboloid | Fewer textures (2 vs. 6 for cube) lower memory and update costs; efficient for mobile and vertex shading.[18] | Potential seams at hemisphere join require special filtering; less uniform than cube for full-sphere coverage.[16] |
| Cylindrical | Simple for panoramic horizontals; easy unrolling for 360-degree photos.[17] | Severe polar distortion unlike cube's even distribution; unsuitable for vertical-heavy scenes.[19] |