IMPLY gate

IMPLY gateMain

Community hub

IMPLY gate

7 pages, 0 posts

0 subscribers

Recent from talks

Be the first to start a discussion here.

Recent from talks

Be the first to start a discussion here.

Contribute something

About hubMembersContent overviewUpdatesRules

Main reference articles

IMPLY gate

View on Wikipedia

from Wikipedia

This article does not cite any sources. Please help improve this article by adding citations to reliable sources. Unsourced material may be challenged and removed.
Find sources: "IMPLY gate" – news · newspapers · books · scholar · JSTOR (August 2020) (Learn how and when to remove this message)

Input A B		Output A → B
0	0	1
0	1	1
1	0	0
1	1	1

The IMPLY gate is a digital logic gate that implements a logical conditional.

Symbols

[edit]

IMPLY can be denoted in algebraic expressions with the logic symbol right-facing arrow (→). Logically, it is equivalent to material implication, and the logical expression ¬A v B.

There are two symbols for IMPLY gates: the traditional symbol and the IEEE symbol. For more information see Logic gate symbols.


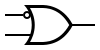
Traditional IMPLY Symbol		IEEE IMPLY Symbol

Functional completeness

[edit]

While the Implication gate is not functionally complete by itself, it is in conjunction with the constant 0 source. This can be shown via the following:

${\begin{aligned}A\rightarrow 0&:=\neg A\\(A\rightarrow 0)\rightarrow B&=\neg (\neg A)\lor B\\&=A\lor B.\end{aligned}}$

Thus, since the implication gate with the addition of the constant 0 source can create both the NOT gate and the OR gate, it can create the NOR gate, which is a universal gate.

View on Grokipedia

from Grokipedia

The IMPLY gate, also known as the implication gate, is a digital logic gate that implements the material implication operation (A → B) on two binary inputs, producing a high output (1) unless the first input A is high (1) and the second input B is low (0), in which case the output is low (0).^[1] This gate corresponds to the logical connective used in classical propositional logic to express conditional statements, where the output evaluates to true in all scenarios except when the antecedent is true but the consequent is false.^[1] The truth table for the IMPLY gate is:

A	B	A → B
0	0	1
0	1	1
1	0	0
1	1	1

This behavior is mathematically equivalent to the Boolean expression ¬A ∨ B, where ¬ denotes negation and ∨ denotes disjunction, allowing the gate to be constructed from more primitive gates like NOT and OR in standard CMOS technology.^[1] Although not as commonly implemented as basic gates like AND, OR, or NAND in conventional digital circuits, the IMPLY gate plays a key role in theoretical Boolean algebra and can be realized in hardware using transistor-level designs or emerging devices. In terms of expressive power, the IMPLY gate alone is not functionally complete, but the set {IMPLY, ⊥}—where ⊥ represents the constant false value (0)—is functionally complete, enabling the realization of any arbitrary Boolean function through compositions of these operations.^[2] This property underscores its utility in minimal logic systems and has motivated its adoption in advanced computing paradigms, particularly memristive stateful logic, where IMPLY operations perform in situ computations within crossbar memory arrays to minimize data transfer overhead between memory and processing units. In such systems, the gate leverages the bistable resistance states of memristors as both inputs and outputs, supporting efficient, non-volatile logic for applications like reconfigurable architectures and in-memory processing.

Definition and Operation

Logical Definition

The IMPLY gate is a binary digital logic gate that realizes material implication, a core operation in propositional logic. Given two inputs, A (the antecedent) and B (the consequent), the gate's output is true if A is false or B is true, and false exclusively when A is true and B is false. This truth-functional behavior ensures the output evaluates to true in three out of four possible input combinations, reflecting the minimal conditions under which a conditional statement holds in classical logic.^[3] In propositional logic, the IMPLY gate functions as a primitive connective that models the indicative conditional ("if A, then B"), but it diverges from everyday notions of implication by prioritizing strict truth-value dependencies over causal or probabilistic interpretations. This distinction underscores its role in formal systems, where it enables the construction of complex logical expressions without assuming real-world entailment.^[3] Material implication originated in ancient Stoic logic, attributed to Philo of Megara in the 3rd century BCE, but received its modern formulation in the late 19th century through Gottlob Frege's Begriffsschrift, which systematized propositional connectives including implication. It was further refined in early 20th-century works like Bertrand Russell and Alfred North Whitehead's Principia Mathematica (1910–1913), integrating it into axiomatic logic. The operation's adaptation to digital gates occurred in the mid-20th century via Boolean algebra, notably through Claude Shannon's 1938 master's thesis, "A Symbolic Analysis of Relay and Switching Circuits," which showed how Boolean algebra could be used to analyze and simplify relay and switching circuits, establishing the basis for digital logic design.^[3]^[4] This logical foundation is prerequisite for analyzing the IMPLY gate's input-output mappings and its practical realizations in computational systems.

Truth Table

The truth table for the IMPLY gate provides a complete mapping of all possible binary input combinations to their corresponding output, using the standard digital logic convention where 0 represents false and 1 represents true.^[5] This table illustrates the gate's behavior as a logical conditional, where the output is 1 (true) unless the first input A is 1 and the second input B is 0.^[6]

A	B	A → B
0	0	1
0	1	1
1	0	0
1	1	1

In the first row, when A=0 and B=0, the output is 1 because a false antecedent makes the implication true regardless of the consequent.^[6] The second row, with A=0 and B=1, also yields 1 for the same reason: the implication holds when the antecedent is false.^[6] In the third row, A=1 and B=0 results in 0, as this is the only case where the implication is false—a true antecedent requires a true consequent to hold.^[6] Finally, when both A=1 and B=1, the output is 1, confirming the implication since the consequent matches the antecedent.^[6] This truth table highlights the asymmetry of the IMPLY gate, where the output is more sensitive to the value of A (the antecedent) than B, as changes in A can flip the output while B primarily affects it only when A=1.

Symbols and Notation

Graphical Symbols

The graphical symbol for the IMPLY gate is not standardized as a primitive in ANSI/IEEE specifications like IEEE Std 91, which cover basic gates. A common representation resembling an OR gate uses a right-pointing triangle with an inversion bubble placed on the line for input A to denote the negated antecedent in the equivalence ¬A ∨ B. The input for A enters from the left side of the triangle, while B connects to the top or side, and the output emerges from the pointed right end.^[7] Alternative symbols include an arrow originating from input A and pointing toward input B, representing the logical implication A → B, often used in theoretical diagrams or mathematical representations.^[8] Custom variants appear in electronic design automation (EDA) tools, such as a basic triangle with a hooked or curved extension on the output side resembling a stylized "J" ending in a dot, adapting the symbol for software simulation while maintaining the two-input, one-output configuration.^[7] In practice, for non-primitive gates like IMPLY, standards such as IEC 60617 often employ rectangular outlines with the function label "IMPLY" inscribed inside, prioritizing textual identification over shape-based intuition. Standard drawing guidelines position input A horizontally on the left for the antecedent, input B vertically or angled from the top for the consequent, and the output extending rightward, ensuring logical flow from left to right in circuit diagrams and alignment with the gate's directional implication semantics. This layout verifies consistency with the truth table, where the symbol's elements correspond to cases yielding true outputs except when A is true and B is false.

Boolean Algebra Expression

The Boolean algebra expression for the IMPLY gate, denoted as

A \rightarrow B

, is

\neg A \lor B

, where

\neg

represents negation and

\lor

represents logical OR.^[9] This formulation captures the logical implication, which holds true unless

A

is true and

B

is false.^[10] This expression derives from the truth table of the IMPLY operation, where the output is 1 for all input combinations except

A = 1

and

B = 0

.^[9] The sole case of output 0 corresponds to

A \land \neg B

; thus, the function is the negation of this conjunction,

\neg (A \land \neg B)

, which simplifies to

\neg A \lor B

via De Morgan's laws.^[9] An alternative notation in Boolean algebra uses prime for negation and plus for OR:

A \rightarrow B = A' + B

.^[11] The IMPLY expression plays a key role in Boolean simplification by allowing reduction through standard algebraic laws, such as distribution and absorption, when embedded in larger circuits.^[10] In Karnaugh maps, it is represented by plotting minterms (e.g.,

\neg A \neg B

\neg A B

A B

) as 1s in a 2-variable grid, then grouping adjacent cells to yield the minimal sum-of-products form

\neg A + B

.^[12]

Functional Properties

Functional Completeness

A set of Boolean connectives is functionally complete if every possible Boolean function can be expressed using only those connectives, allowing the realization of any truth table through compositions thereof.^[13] The IMPLY gate, corresponding to material implication

A \to B \equiv \neg A \lor B

, is not functionally complete by itself, as it preserves the constant 1 (all-1 vector) and thus cannot generate functions like negation that falsify when all inputs are true.^[14] However, adjoining the constant 0 (false) to the IMPLY gate yields a functionally complete set, as established by Post's functional completeness theorem, which characterizes complete systems via their ability to escape five specific classes of functions (preserving 0, preserving 1, linear, monotone, and self-dual).^[13] To illustrate, the NOT gate (

\neg A

) is constructed directly as

A \to 0

, since

\neg A \lor 0 \equiv \neg A

. With NOT available, the OR gate (

A \lor B

) follows from

(A \to B) \to B

, which simplifies to

\neg(\neg A \lor B) \lor B \equiv A \lor B

. Alternatively, using the derived NOT,

A \lor B \equiv \neg(\neg A \land \neg B)

, where the inner AND is addressed below. The AND gate (

A \land B

) is obtained as

(A \to (B \to 0)) \to 0

, since

A \to \neg B \equiv \neg A \lor \neg B \equiv \neg(A \land B)

, and negating yields the conjunction. These constructions enable NOT, AND, and OR (or equivalently NAND via

\neg(A \land B)

), a known complete basis, thus proving the expressive power of {IMPLY, 0}.^[14] This property aligns with the broader framework of Post's lattice of functional completeness, where implication joined with a non-1-preserving constant like 0 escapes the preservation classes to achieve completeness.^[13] The recognition of implication-based complete systems traces to Emil Post's foundational work in the 1920s and 1940s on iterative systems and truth-functional completeness in mathematical logic.

Equivalence to Other Operations

The IMPLY operation, also known as material implication and denoted as

A \to B

, is logically equivalent to the negation of the conjunction of

A

and the negation of

B

, expressed as

\neg (A \wedge \neg B)

.^[15] This equivalence arises because the implication is false only when the antecedent

A

is true and the consequent

B

is false, which precisely matches the condition under which

A \wedge \neg B

holds.^[16] It is also equivalent to the disjunction

\neg A \vee B

, as both expressions yield the same truth values across all input combinations.^[16] A related operation is the biconditional, or logical equivalence, denoted

A \leftrightarrow B

, which holds when

A

and

B

have the same truth value. This can be constructed using two IMPLY operations as

(A \to B) \wedge (B \to A)

, ensuring mutual implication between the propositions.^[16] In contrast, the contrapositive of an IMPLY statement

A \to B

\neg B \to \neg A

, which is logically equivalent to the original implication, preserving its truth value regardless of the specific inputs.^[16] Unlike symmetric operations such as exclusive OR (XOR, denoted

A \oplus B

), which outputs true only when the inputs differ and is commutative (

A \oplus B = B \oplus A

), the IMPLY operation is asymmetric (

A \to B \neq B \to A

in general) and outputs true in three of the four possible input combinations, specifically failing only when

A

is true and

B

is false.^[16] Similarly, the exclusive NOR (XNOR, or equivalence,

A \odot B

) is symmetric and outputs true when inputs match, differing fundamentally from IMPLY's directed, truth-preserving nature in most cases.^[16]

Implementations and Applications

Hardware Implementation

The IMPLY gate, realizing the logical implication function

A \rightarrow B \equiv \neg A \lor B

, can be constructed using NAND gates, which are universal building blocks in digital electronics. Specifically, the function is equivalent to a NAND operation between input

A

and the negation of

B

, where

\neg B

is obtained by tying both inputs of a NAND gate to

B

to form an inverter. This requires two 2-input NAND gates: one acting as the inverter for

B

, and the second performing the NAND of

A

and

\neg B

. At the transistor level, a CMOS implementation of the IMPLY gate typically employs 6 transistors, comprising an integrated inverter (2 transistors) followed by a 2-input NAND stage (4 transistors), with the pull-up and pull-down networks configured to mirror the

\neg A \lor B

expression. The pull-down network consists of two NMOS transistors in series gated by

A

and

\neg B

, while the pull-up network uses two PMOS transistors in parallel gated by

A

and

\neg B

, ensuring complementary operation for low static power dissipation. This design aligns with standard static CMOS practices for complex gates.^[17] Propagation delay in such CMOS IMPLY gates is comparable to that of equivalent AND-OR structures, typically ranging from 50 ps to a few hundred picoseconds in modern processes like 45 nm or below, depending on load capacitance and supply voltage; for instance, simulations show an average delay of about 50 ps under standard conditions. Power consumption remains low due to CMOS's complementary switching, with dynamic power dominating during transitions and static power near zero when idle, making it suitable for dense VLSI integration.^[17]^[18] The IMPLY gate has also been implemented using memristors in crossbar arrays for stateful logic, enabling in situ computations that reduce data movement between memory and processors. In memristive IMPLY, two memristors and a resistor form the gate, with resistance states representing logic values; the operation performs material implication directly on the device, supporting efficient in-memory processing in reconfigurable architectures.^[19] In field-programmable gate arrays (FPGAs), the IMPLY gate is realized through configurable lookup tables (LUTs), where a 2-input LUT stores the four possible output values from the IMPLY truth table in its memory bits, enabling any 2-variable Boolean function to be programmed via configuration data. This approach leverages the reconfigurability of SRAM-based LUTs, typically using 16 bits for a 4-input LUT but simplified to 4 bits for 2 inputs like IMPLY, with minimal additional routing overhead.^[20]

Software and Theoretical Uses

In software applications, the IMPLY operation, equivalent to material implication (¬A ∨ B), finds utility in constraint satisfaction problems, particularly within Boolean satisfiability (SAT) solvers. These solvers leverage implication graphs to propagate constraints and detect conflicts efficiently during the decision-making process, enabling the resolution of complex logical formulas in verification tasks.^[21] For instance, modern SAT solvers like MiniSat or Glucose use unit propagation based on implied literals to simplify clauses, reducing the search space in problems from hardware design to software testing.^[22] In rule-based programming systems, such as Prolog, implication forms the core of rule definitions, where the :- operator expresses Horn clauses as "if body then head," facilitating declarative logic programming for knowledge representation and inference. This structure allows Prolog interpreters to perform backward chaining, unifying goals with rule antecedents to derive conclusions in applications like expert systems.^[23] Prolog's implication-based rules enable efficient querying of relational data, mirroring the logical foundations of databases. Theoretically, IMPLY underpins automated theorem proving through resolution methods, where clauses are treated as disjunctive implications, allowing refutation-complete proofs by resolving complementary literals to eliminate variables. Seminal work by Robinson formalized resolution in 1965, enabling systems like Otter to handle first-order logic problems by converting implications into clausal form for efficient deduction.^[24] In fuzzy logic extensions, IMPLY generalizes to implication operators derived from t-norms and s-norms, such as the Gödel or Łukasiewicz implications, which model gradual reasoning in uncertain environments for control systems and decision-making. These operators satisfy properties like contraposition and exchange, extending classical IMPLY to handle partial truths in multi-valued logics.^[25] Practical examples include AI planning, where the STRIPS framework employs implication-like operators, with preconditions implying state transitions (if preconditions hold, then apply add/delete effects), forming the basis for hierarchical task networks in robotic pathfinding and scheduling.^[26] This representational power, rooted in functional completeness with other gates, supports expressive planning languages like PDDL. Despite these strengths, IMPLY is less prevalent in low-level programming languages like C or assembly, where native bitwise AND and OR operations suffice for efficient implementation, rendering direct implication constructs redundant and potentially less intuitive due to its vacuous truth when the antecedent is false. However, it remains valuable in high-level logic languages for abstract reasoning, avoiding the need to decompose into disjunctions manually.^[27]

v t e Common logical connectives
Tautology/True $\top$
Alternative denial (NAND gate) ${\overline {\wedge }}$ Converse implication $\Leftarrow$ Implication (IMPLY gate) $\Rightarrow$ Disjunction (OR gate) $\lor$
Negation (NOT gate) $\neg$ Exclusive or (XOR gate) $\oplus$ Biconditional (XNOR gate) $\odot$ Statement (Digital buffer)
Joint denial (NOR gate) ${\overline {\vee }}$ Nonimplication (NIMPLY gate) $\nRightarrow$ Converse nonimplication $\nLeftarrow$ Conjunction (AND gate) $\land$
Contradiction/False $\bot$
Philosophy portal

Info Pages

Talk Pages

Special Pages

IMPLY gate

Recent from talks

Recent from talks

Contribute something

Contribute something

Media Pages

Timelines

Articles

Notes collections

Notes

Notes

Days in Chronicle

IMPLY gate

Symbols

Functional completeness

See also

IMPLY gate

Definition and Operation

Logical Definition

Truth Table

Symbols and Notation

Graphical Symbols

Boolean Algebra Expression

Functional Properties

Functional Completeness

Equivalence to Other Operations

Implementations and Applications

Hardware Implementation

Software and Theoretical Uses

References

Add your contribution

Related Hubs

Contribute something

History

IMPLY gate

Recent from talks

Recent from talks

Contribute something

Contribute something

Media Pages

Timelines

Articles

Notes collections

Notes

Notes

Days in Chronicle

IMPLY gate

Symbols

Functional completeness

See also

IMPLY gate

Definition and Operation

Logical Definition

Truth Table

Symbols and Notation

Graphical Symbols

Boolean Algebra Expression

Functional Properties

Functional Completeness

Equivalence to Other Operations

Implementations and Applications

Hardware Implementation

Software and Theoretical Uses

References

Add your contribution

Related Hubs

Contribute something