Minimum deviation

In a prism, the angle of deviation ( $δ$ ) decreases with increase in the angle of incidence ( $i$ ) up to a particular angle. This angle of incidence where the angle of deviation in a prism is minimum is called the minimum deviation position of the prism and that very deviation angle is known as the minimum angle of deviation (denoted by $δ min$ , $D λ$ , or $D m$ ).

The angle of minimum deviation is related with the refractive index as:

$n_{21}={\dfrac {\sin \left({\dfrac {A+D_{m}}{2}}\right)}{\sin \left({\dfrac {A}{2}}\right)}}$

This is useful to calculate the refractive index of a material. Rainbow and halo occur at minimum deviation. Also, a thin prism is always set at minimum deviation.

Formula

In minimum deviation, the refracted ray in the prism is parallel to its base. In other words, the light ray is symmetrical about the axis of symmetry of the prism.^[1]^[2]^[3] Also, the angles of refractions are equal i.e. $r 1 = r 2$ . The angle of incidence and angle of emergence equal each other ( $i = e$ ). This is clearly visible in the graph below.

The formula for minimum deviation can be derived by exploiting the geometry in the prism. The approach involves replacing the variables in the Snell's law in terms of the Deviation and Prism Angles by making the use of the above properties.

From the angle sum of ${\textstyle \triangle OPQ}$ ,

$A+\angle OPQ+\angle OQP=180^{\circ }$ $\implies A=180^{\circ }-(90-r)-(90-r)$ $\implies r={\frac {A}{2}}$

Using the exterior angle theorem in ${\textstyle \triangle PQR}$ ,

$D_{m}=\angle RPQ+\angle RQP$ $\implies D_{m}=i-r+i-r$ $\implies 2r+D_{m}=2i$ $\implies A+D_{m}=2i$ $\implies i={\frac {A+D_{m}}{2}}$

This can also be derived by putting $i = e$ in the prism formula: $i + e = A + δ$

From Snell's law,

$n_{21}={\dfrac {\sin i}{\sin r}}$

$\therefore n_{21}={\dfrac {\sin \left({\dfrac {A+D_{m}}{2}}\right)}{\sin \left({\dfrac {A}{2}}\right)}}$ ^[4]^[3]^[1]^[2]^[5]^{[excessive citations]}

$\therefore D_{m}=2\sin ^{-1}\left(n\sin \left({\frac {A}{2}}\right)\right)-A$

(where $n$ is the refractive index, $A$ is the Angle of Prism and $D m$ is the Minimum Angle of Deviation.)

This is a convenient way used to measure the refractive index of a material(liquid or gas) by directing a light ray through a prism of negligible thickness at minimum deviation filled with the material or in a glass prism dipped in it.^[5]^[3]^[1]

Worked out examples:

The refractive index of glass is 1.5. The minimum angle of deviation for an equilateral prism along with the corresponding angle of incidence is desired.

Answer: 37°, 49°

Solution:

Here, $A = 60°$ , $n = 1.5$

Plugging them in the above formula,

${\textstyle {\frac {\sin \left({\frac {60+\delta }{2}}\right)}{\sin \left({\frac {60}{2}}\right)}}=1.5}$

${\textstyle \implies {\frac {\sin \left(30+{\frac {\delta }{2}}\right)}{\sin(30)}}=1.5}$

${\textstyle \implies \sin \left(30+{\frac {\delta }{2}}\right)=1.5\times 0.5}$

${\textstyle \implies 30+{\frac {\delta }{2}}=\sin ^{-1}(0.75)}$

${\textstyle \implies {\frac {\delta }{2}}=48.6-30}$

${\textstyle \implies \delta =2\times 18.6}$

${\textstyle \therefore \delta \approx 37^{\circ }}$

Also,

${\textstyle i={\frac {(A+\delta )}{2}}={\frac {60+2\times 18.6}{2}}\approx 49^{\circ }}$

This is also apparent in the graph below.

If the minimum angle of deviation of a prism of refractive index 1.4 equals its refracting angle, the angle of the prism is desired.

Answer: 60°

Solution:

Here, ${\textstyle \delta =r}$

${\textstyle \implies \delta ={\frac {A}{2}}}$

Using the above formula,

${\textstyle {\frac {\sin \left({\frac {A+{\frac {A}{2}}}{2}}\right)}{\sin \left({\frac {A}{2}}\right)}}=1.4}$

${\textstyle \implies {\frac {\sin \left({\frac {3A}{4}}\right)}{\sin \left({\frac {A}{2}}\right)}}={\frac {\frac {1}{2}}{\frac {1}{\sqrt {2}}}}}$

${\textstyle \implies {\frac {\sin \left({\frac {3A}{4}}\right)}{\sin \left({\frac {A}{2}}\right)}}={\frac {\sin 45^{\circ }}{\sin 30^{\circ }}}}$

${\textstyle \therefore A=60^{\circ }}$

Also, the variation of the angle of deviation with an arbitrary angle of incidence can be encapsulated into a single equation by expressing δ in terms of $i$ in the prism formula using Snell's law:

$\delta =i-A+\sin ^{-1}\left(n\cdot \sin \left(A-\sin ^{-1}\left({\frac {\sin i}{n}}\right)\right)\right)=f(i)$

Finding the minima of this equation will also give the same relation for minimum deviation as above.

Putting $f'(i)=0$ , we get,

${\frac {\cos \left(A-\sin ^{-1}\left({\frac {\sin i}{u}}\right)\right)\cos i}{\sqrt {\left(1-u^{2}\sin ^{2}\left(A-\sin ^{-1}\left({\frac {\sin i}{u}}\right)\right)\right)\left(1-{\frac {\sin ^{2}i}{u^{2}}}\right)}}}=1$ , and by solving this equation we can obtain the value of angle of incidence for a definite value of angle of prism and the value of relative refractive index of the prism for which the minimum angle of deviation will be obtained. The equation and description are given here

For thin prism

In a thin or small angle prism, as the angles become very small, the sine of the angle nearly equals the angle itself and this yields many useful results.

Because $D m$ and $A$ are very small,

${\begin{aligned}n&\approx {\dfrac {\frac {A+D_{m}}{2}}{\frac {A}{2}}}\\n&={\frac {A+D_{m}}{A}}\\D_{m}&=An-A\end{aligned}}$

$\therefore D_{m}=A(n-1)$ ^[1]^[4]

Using a similar approach with the Snell's law and the prism formula for an in general thin-prism ends up in the very same result for the deviation angle.

Because $i$ , $e$ and $r$ are small,

$n\approx {\frac {i}{r_{1}}},n\approx {\frac {e}{r_{2}}}$

From the prism formula, ${\begin{aligned}\delta &=nr_{1}+nr_{2}-A\\&=n(r_{1}+r_{2})-A\\&=nA-A\\&=A(n-1)\end{aligned}}$

Thus, it can be said that a thin prism is always in minimum deviation.

Experimental determination

Minimum deviation can be found manually or with spectrometer. Either the prism is kept fixed and the incidence angle is adjusted or the prism is rotated keeping the light source fixed.^[6]^[7]^[8]

Minimum angle of dispersion

The minimum angle of dispersion for white light is the difference in minimum deviation angle between red and violet rays of a light ray through a prism.^[2]

For a thin prism, the deviation of violet light, $\delta _{v}$ is $(n_{v}-1)A$ and that of red light, $\delta _{r}$ is $(n_{r}-1)A$ . The difference in the deviation between red and violet light, $(\delta _{v}-\delta _{r})=(n_{v}-n_{r})A$ is called the Angular Dispersion produced by the prism.

Applications

Drawing radii to the points of interference reveals that the angles of refraction are equal, thereby proving minimum deviation.

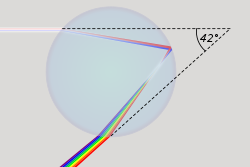
One of the factors that causes a rainbow is the bunching of light rays at the minimum deviation angle that is close to the rainbow angle (42°).^[3]^[9]

It is also responsible for phenomena like halos and sundogs, produced by the deviation of sunlight in mini prisms of hexagonal ice crystals in the air bending light with a minimum deviation of 22°.^[3]^[10]

References

^ ^a ^b ^c ^d "Chapter Nine, RAY OPTICS AND OPTICAL INSTRUMENTS". Physics Part II Textbook for Class IX (PDF). NCERT. p. 331.
^ ^a ^b ^c "Optics-Prism". A-Level Physics Tutor.
^ ^a ^b ^c ^d ^e Mark A. Peterson. "Minimum Deviation by a Prism". mtholyoke. Mount Holyoke College. Archived from the original on 2019-05-23.
^ ^a ^b "Refraction through Prisms". SchoolPhysics.
^ ^a ^b "Prism". HyperPhysics.
^ "Angle of Minimum Deviation". Scribd.
^ "Experimental set up for the measurements of angle of minimum deviation using prism spectrometer". ResearchGate.
^ "Theory of the Prism Spectrometer - Experiment | UKEssays.com". www.ukessays.com. Retrieved 2025-03-11.
^ "Rainbow". www.schoolphysics.co.uk.
^ "Halo 22°". HyperPhysics.

External links

Minimum Deviation Part 1 and Part 2 at Khan Academy
Refraction through a Prism in NCERT Textbook
Minimum Deviation by Prism Archived 2019-05-23 at the Wayback Machine by Mark A Peterson, Mount Holyoke College

[:1-1] "Chapter Nine, RAY OPTICS AND OPTICAL INSTRUMENTS". Physics Part II Textbook for Class IX (PDF). NCERT. p. 331.

[:2-2] "Optics-Prism". A-Level Physics Tutor.

[:0-3] Mark A. Peterson. "Minimum Deviation by a Prism". mtholyoke. Mount Holyoke College. Archived from the original on 2019-05-23.

[:3-4] "Refraction through Prisms". SchoolPhysics.

[:4-5] "Prism". HyperPhysics.

[6] "Angle of Minimum Deviation". Scribd.

[7] "Experimental set up for the measurements of angle of minimum deviation using prism spectrometer". ResearchGate.

[8] "Theory of the Prism Spectrometer - Experiment | UKEssays.com". www.ukessays.com. Retrieved 2025-03-11.

[9] "Rainbow". www.schoolphysics.co.uk.

[10] "Halo 22°". HyperPhysics.

[1]

[2]

[3]

[4]

[5]

[6]

[7]

[8]

[9]

[10]

History

Media collections

Minimum deviation

Recent from talks

Recent from talks

Contribute something

Contribute something

Media Pages

Timelines

Articles

Notes collections

Notes

Notes

Days in Chronicle

Minimum deviation

Formula

For thin prism

Experimental determination

Minimum angle of dispersion

Applications

See also

References

External links