Hubbry Logo
NOR logicNOR logicMain
Open search
NOR logic
Community hub
NOR logic
logo
8 pages, 0 posts
0 subscribers
Be the first to start a discussion here.
Be the first to start a discussion here.
NOR logic
NOR logic
NOR logic
View on Wikipedia
from Wikipedia
A single NOR gate

A NOR gate or a NOT OR gate is a logic gate which gives a positive output only when both inputs are negative.

Like NAND gates, NOR gates are so-called "universal gates" that can be combined to form any other kind of logic gate. For example, the first embedded system, the Apollo Guidance Computer, was built exclusively from NOR gates, about 5,600 in total for the later versions. Today, integrated circuits are not constructed exclusively from a single type of gate. Instead, EDA tools are used to convert the description of a logical circuit to a netlist of complex gates (standard cells) or transistors (full custom approach).

NOR

[edit]
Main article: NOR gate

A NOR gate is logically an inverted OR gate. It has the following truth table:[1]

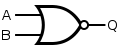
Q = A NOR B

Truth Table
Input A Input B Output Q
0 0 1
0 1 0
1 0 0
1 1 0

Making other gates by using NOR gates

[edit]

A NOR gate is a universal gate, meaning that any other gate can be represented as a combination of NOR gates.

NOT

[edit]
See also: NOT gate

This is made by joining the inputs of a NOR gate. As a NOR gate is equivalent to an OR gate leading to NOT gate, joining the inputs makes the output of the "OR" part of the NOR gate the same as the input, eliminating it from consideration and leaving only the NOT part.

Desired NOT Gate NOR Construction
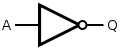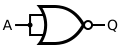
Q = NOT( A ) = A NOR A
Truth Table
Input A Output Q
0 1
1 0

OR

[edit]
See also: OR gate

An OR gate is made by inverting the output of a NOR gate. Note that we already know that a NOT gate is equivalent to a NOR gate with its inputs joined.

Desired OR Gate NOR Construction
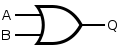Q = A OR B = ( A NOR B ) NOR ( A NOR B )
Truth Table
Input A Input B Output Q
0 0 0
0 1 1
1 0 1
1 1 1

AND

[edit]
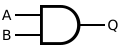
See also: AND gate

An AND gate gives a 1 output when both inputs are 1. Therefore, an AND gate is made by inverting the inputs of a NOR gate. Again, note that a NOR gate is equivalent to a NOT with its inputs joined.

Desired AND Gate NOR Construction
Q = A AND B = ( A NOR A ) NOR ( B NOR B )
Truth Table
Input A Input B Output Q
0 0 0
0 1 0
1 0 0
1 1 1

NAND

[edit]
See also: NAND gate

A NAND gate is made by inverting the output of an AND gate. The word NAND means that it is not AND. As the name suggests, it will give 0 when both the inputs are 1.

Desired NAND Gate NOR Construction
Q = A NAND B = [ ( A NOR A ) NOR ( B NOR B ) ] NOR
[ ( A NOR A ) NOR ( B NOR B ) ]
Truth Table
Input A Input B Output Q
0 0 1
0 1 1
1 0 1
1 1 0

XNOR

[edit]
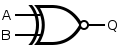
See also: XNOR gate

An XNOR gate is made by connecting four NOR gates as shown below. This construction entails a propagation delay three times that of a single NOR gate.

Desired XNOR Gate NOR Construction
Q = A XNOR B = [ A NOR ( A NOR B ) ] NOR
[ B NOR ( A NOR B ) ]
Truth Table
Input A Input B Output Q
0 0 1
0 1 0
1 0 0
1 1 1

Alternatively, an XNOR gate is made by considering the conjunctive normal form , noting from de Morgan's Law that a NOR gate is an inverted-input AND gate. This construction uses five gates instead of four.

Desired Gate NOR Construction
Q = A XNOR B = [ B NOR ( A NOR A ) ] NOR
[ A NOR ( B NOR B ) ]

XOR

[edit]
See also: XOR gate

An XOR gate is made by considering the conjunctive normal form , noting from de Morgan's Law that a NOR gate is an inverted-input OR gate. This construction entails a propagation delay three times that of a single NOR gate and uses five gates.

Desired XOR Gate NOR Construction
Q = A XOR B = [ ( A NOR A ) NOR ( B NOR B ) ] NOR
( A NOR B )
Truth Table
Input A Input B Output Q
0 0 0
0 1 1
1 0 1
1 1 0

Alternatively, the 4-gate version of the XNOR gate can be used with an inverter. This construction has a propagation delay four times (instead of three times) that of a single NOR gate.

Desired Gate NOR Construction
Q = A XOR B = { [ A NOR ( A NOR B ) ] NOR
[ B NOR ( A NOR B ) ] } NOR
{ [ A NOR ( A NOR B ) ]
NOR [ B NOR ( A NOR B ) ] }

See also

[edit]

References

[edit]
Revisions and contributorsEdit on WikipediaRead on Wikipedia

NOR logic

View on Grokipedia
from Grokipedia
NOR logic, also referred to as logic, centers on the , a basic digital that performs the of the disjunction (OR) operation on one or more binary inputs, yielding a high output (logic 1) exclusively when all inputs are low (logic 0). This gate is electrically realized in integrated circuits using complementary arrangements of transistors, such as in technology where parallel n-channel transistors pull the output low if any input is high, and series-connected p-channel transistors pull it high only if all inputs are low. A defining feature of the is its , allowing it to serve as a universal gate from which all other logic functions—including , and NOT—can be constructed without additional gate types. This universality stems from the ability to derive basic operations using combinations of NOR gates: for instance, a NOT gate by connecting both inputs of a two-input NOR to the same signal, an by NORing a NOR output with itself (via ), and an through further NOR compositions. The foundational insight into such completeness in switching circuits was provided by in his 1938 master's thesis, which demonstrated that relay and switching circuits could be analyzed and synthesized using to implement any logical function, bridging with practical . The functional completeness of the follows from this foundational work. In digital electronics, NOR logic is widely employed due to its efficiency in VLSI design, where minimizing gate count and usage reduces power consumption and chip area; for example, multi-input NOR gates are straightforward to implement in with scalable pull-down networks. It underpins key components like SR latches in sequential circuits, where cross-coupled NOR gates provide stable memory elements for flip-flops and registers. Historically, NOR-based designs gained prominence in early computing systems reliant on or vacuum-tube technology, and today they remain integral to memory elements, programmable logic devices, and fault-tolerant architectures owing to their simplicity and robustness.

Fundamentals

Definition and Functionality

In digital electronics, logic gates serve as the fundamental building blocks for constructing circuits that process binary signals, where is represented using two distinct voltage levels: low (0, corresponding to false or off) and high (1, corresponding to true or on). These gates perform specific operations on one or more input signals to produce a single output signal, enabling the implementation of complex computational functions in computers and other electronic devices. The , short for "NOT-OR," is a specific type of that outputs a high signal (1) only when all of its inputs are low (); in all other cases, the output is low (). This behavior represents the logical of the OR operation, where the itself would output high (1) if at least one input is high, and the NOR inverts that result. As such, the effectively computes the complement of the inclusive OR function across its inputs, making it a versatile primitive in . NOR gates are not limited to two inputs and can be designed with three or more inputs, maintaining the same principle: the output remains high (1) exclusively when every single input is low (0), and drops to low (0) if any input is high. This allows NOR gates to handle multiple signals in integrated circuits, where the gate's output reflects the absence of activity across all inputs. For instance, consider a two-input NOR gate modeling a safety system, such as an that activates (outputs 1) only if both sensors detect no intrusion (both inputs 0), remaining silent (output 0) if either sensor triggers.

Symbols and Circuit Representation

The standard graphical representation of a NOR gate follows the ANSI/IEEE Std 91-1984, which uses a distinctive curved shape resembling an OR gate—typically a concave arc with multiple input lines on the left side and output on the right side—combined with a small circular bubble at the output to indicate inversion. This bubble, known as a negation qualifier, denotes that the output is the logical complement of the OR operation, transforming an active-high OR into an active-low NOR. Alternative symbols include the IEC 60617 standard, which employs a rectangular box for the gate outline, with inputs on the left, an output on the right, and a circular inversion marker at the output; the interior may feature a ">1" notation to signify the OR function before negation. Historical variations encompass the older MIL-STD-806B military symbols, which are similar to the ANSI/IEEE distinctive shapes but with more rigid geometric constraints for schematic clarity in defense applications, and the obsolete DIN 40700 standard used in , featuring a rectangular form akin to IEC. At the circuit level, a two-input in technology is implemented using four transistors: two p-channel MOSFETs (PMOS) connected in series between the power supply and output for the pull-up network, and two n-channel MOSFETs (NMOS) connected in parallel between the output and ground for the pull-down network. In TTL implementations, the gate typically employs a multi-emitter (BJT) for the inputs, followed by additional BJTs in a totem-pole configuration to drive the output, enabling efficient switching with standard 5V logic levels. Symbols for NOR gates adhere to active-high conventions for inputs by default, where a logic high (typically 3.5–5V) asserts the signal without bubbles on input lines; however, the output bubble denotes the inversion of the OR function, resulting in a high output when the internal OR is false (all inputs low). In standard active-high logic, both inputs and output are active-high. Bubbles or triangular polarity indicators on inputs would denote active-low inputs, inverting the signal before , while such qualifiers ensure compatibility across positive and negative logic systems in mixed-signal designs.

Truth Table and Boolean Expression

The logical operation performed by a two-input NOR gate is specified by its , which lists all possible combinations of input values and the resulting output. The table is as follows:
Input AInput BOutput
001
010
100
110
This demonstrates that the output is 1 only when both are 0; in all other cases, the output is 0. The for the two-input can be derived directly from the truth table by identifying the input conditions under which the output is 1. The sole minterm where the output is 1 corresponds to A = 0 and B = 0, yielding the sum-of-products form A‾⋅B‾\overline{A} \cdot \overline{B}. Recognizing that this condition is the of the OR operation (where A ∨ B = 0 only when both inputs are 0), the expression simplifies to A∨B‾\overline{A \lor B}. By , A∨B‾\overline{A \lor B} is logically equivalent to A‾∧B‾\overline{A} \land \overline{B}, providing an alternative algebraic representation that emphasizes the conjunction of negated inputs. For a multi-input NOR gate with n inputs (A₁, A₂, ..., Aₙ), the output is 1 all inputs are 0; otherwise, it is 0. The general is A1∨A2∨⋯∨An‾\overline{A_1 \lor A_2 \lor \dots \lor A_n}, which extends the two-input form by including additional disjuncts.

Universality

Functional Completeness

Functional completeness refers to the property of a set of logical connectives that allows the expression of any arbitrary Boolean function using only combinations of those connectives. In digital logic, a single gate type possesses functional completeness if it alone can implement all possible Boolean operations, thereby serving as a universal gate. The NOR gate exhibits this property because it can generate the negation (NOT), conjunction (AND), and disjunction (OR) operations, which together form a functionally complete set. To demonstrate this, consider the construction of each basic operation using NOR gates. The NOT operation is realized by connecting both inputs of a single NOR gate to the input signal AA: A‾=A↓A\overline{A} = A \downarrow A where ↓\downarrow denotes the NOR operation, equivalent to A∨A‾=A‾\overline{A \lor A} = \overline{A}. This uses one NOR gate. The OR operation requires two NOR gates. First, apply NOR to inputs AA and BB to obtain A∨B‾\overline{A \lor B}. Then, apply NOT to this result by feeding it to both inputs of a second NOR gate: A∨B=(A↓B)↓(A↓B)=A∨B‾‾=A∨B.A \lor B = (A \downarrow B) \downarrow (A \downarrow B) = \overline{\overline{A \lor B}} = A \lor B. This configuration inverts the NOR output to yield the desired OR. For the AND operation, three NOR gates are used, leveraging De Morgan's law: A∧B=A‾∨B‾‾A \land B = \overline{\overline{A} \lor \overline{B}}. First, compute A‾\overline{A} and B‾\overline{B} using two separate NOR gates as described for NOT. Then, feed these inverted signals into a third NOR gate: A∧B=(A‾)↓(B‾)=A‾∨B‾‾=A∧B.A \land B = (\overline{A}) \downarrow (\overline{B}) = \overline{\overline{A} \lor \overline{B}} = A \land B. This step-by-step construction confirms that AND can be expressed via NOR gates. Emil Post's functional completeness theorem provides a formal characterization, stating that a set of connectives is functionally complete it is not a subset of any of the five maximal clones in the Post lattice of functions—specifically, those closed under true (T), false (F), monotonicity, , or self-duality. The NOR connective violates all five properties: it maps all-true inputs to false, all-false to true, is non-monotonic (e.g., increasing one input can change output from false to true), is nonlinear, and is not self-dual (its does not match the dual when inputs are complemented). Thus, {NOR} generates the full lattice, confirming its primitive recursive completeness for all functions.

Comparison to NAND and Other Gates

NOR logic gates share functional completeness with NAND gates, both serving as universal building blocks for constructing any Boolean function, though NAND outputs a logic 1 unless all inputs are 1, in contrast to NOR's output of 1 only when all inputs are 0. This duality arises from De Morgan's laws, where NOR is the complement of OR and NAND is the complement of AND, enabling symmetric yet inverse behaviors in circuit design. In CMOS implementations, NOR gates typically favor pull-down networks, which can simplify designs for higher fan-ins due to parallel NMOS transistors, while NAND gates prefer pull-up networks with parallel PMOS for similar reasons, leading to trade-offs in area and speed. Propagation delays for NOR gates are often longer in high-fan-in scenarios because of series PMOS paths in the pull-up network, whereas NAND gates can exhibit different delay characteristics due to series NMOS in the pull-down; power consumption is comparable but varies with process technology. The following table summarizes key comparisons between NOR, NAND, AND, and OR gates:
Gate TypeUniversalityInput Count EfficiencyCommon Uses
NORYesHigh for OR-like functions; scales well in pull-down Memory cells (e.g., NOR flash), PLA decoders
NANDYesHigh for AND-like functions; efficient in pull-up Standard SSI logic, adders, multiplexers
ANDNoLow; requires inversion for completenessBasic , but not universal
ORNoLow; limited without complementsSignal merging, but paired with NOT for universality
In TTL logic families, both NOR and NAND gates have a of 10 standard loads due to their totem-pole output structures, supporting reliable drive in bus-oriented designs. Both NOR and NAND remain in use today—NOR for specialized applications like programmable logic arrays (PLAs) where parallel decoding is advantageous, and NAND for general small-scale integration (SSI) due to its prevalence in libraries.

Constructing Other Logic Gates

NOT, OR, and AND Gates

The NOT gate can be constructed using a single NOR gate by connecting one input to the input signal A and the other input to logic 0 (ground). The output is then ¬(A∨0)=¬A\neg (A \lor 0) = \neg A, which inverts the input as required for a NOT gate. An OR gate requires two NOR gates for implementation. The first NOR gate takes inputs A and B, producing an output of ¬(A∨B)\neg (A \lor B). This output is fed into the second NOR gate along with logic 0 on the other input, yielding ¬(¬(A∨B)∨0)=A∨B\neg (\neg (A \lor B) \lor 0) = A \lor B. In circuit terms: NOR1 inputs are A and B; NOR2 inputs are the output of NOR1 and 0. The is built using three NOR gates, applying De Morgan's theorem: A∧B=¬(¬A∨¬B)A \land B = \neg (\neg A \lor \neg B). The first NOR gate inverts A by taking inputs A and 0, producing ¬A\neg A. The second NOR gate similarly inverts B, producing ¬B\neg B. The third NOR gate takes ¬A\neg A and ¬B\neg B as inputs, outputting ¬(¬A∨¬B)=A∧B\neg (\neg A \lor \neg B) = A \land B. In circuit terms: NOR1 inputs are A and 0; NOR2 inputs are B and 0; NOR3 inputs are outputs of NOR1 and NOR2. These constructions demonstrate the minimal number of NOR gates needed: one for NOT, two for OR, and three for AND. These basic gate constructions using NOR gates form the foundation for realizing any Boolean function, underscoring the functional completeness of the NOR gate in digital circuit design.

NAND and NOR Gates

To construct a NAND gate using only NOR gates, four two-input NOR gates are required. The first two NOR gates act as inverters to produce the complements of the inputs: A‾=NOR(A,A)\overline{A} = \text{NOR}(A, A) and B‾=NOR(B,B)\overline{B} = \text{NOR}(B, B). These complemented signals are then fed into a third NOR gate, yielding NOR(A‾,B‾)=A‾∨B‾‾=A∧B\text{NOR}(\overline{A}, \overline{B}) = \overline{\overline{A} \lor \overline{B}} = A \land B. Finally, the output of this gate is inverted using a fourth NOR gate configured as a NOT: A∧B‾=NOR(A∧B,A∧B)\overline{A \land B} = \text{NOR}(A \land B, A \land B), which produces the NAND function. This construction can be verified using De Morgan's theorem, which states that A∧B‾=A‾∨B‾\overline{A \land B} = \overline{A} \lor \overline{B}. The circuit effectively computes A‾∨B‾\overline{A} \lor \overline{B} through the intermediate AND followed by inversion, equivalent to the direct disjunction of complements, confirming the NAND output for all input combinations (e.g., when A=1A=1 and B=1B=1, the result is 0; otherwise, 1). In contrast to basic gates like NOT (one NOR), OR (two NORs), and AND (three NORs), the NAND requires four NOR gates, underscoring a relative inefficiency in this but demonstrating NOR's versatility as a universal gate for compound functions. The construction of a from NOR gates is trivial, requiring only a single gate, as it is the primitive itself. This inclusion serves for completeness in discussions of universal gate sets, ensuring all standard logic operations can be systematically derived without assuming primitives beyond two-input NOR. For multi-input NOR gates, such as a three- or four-input version, a single multi-input NOR primitive is often used in practice for efficiency. However, when restricted to two-input NOR gates, a can build the equivalent by first constructing a multi-input OR (via cascaded two-input OR subcircuits, each using two NORs) and then applying a final NOT using one NOR. For a four-input NOR, this requires three two-input ORs (six NORs) plus one NOT (one NOR), totaling seven gates, though optimized designs may reduce this in integrated circuits.

XOR and XNOR Gates

The XOR gate performs an exclusive disjunction operation, producing an output of 1 when its two inputs differ. Its is A⊕B=(A∨B)∧¬(A∧B)A \oplus B = (A \lor B) \land \lnot (A \land B). This can be realized using five 2-input s in a multilevel circuit. The construction begins with a NOR gate taking inputs A and B to produce intermediate signal P=¬(A∨B)P = \lnot (A \lor B). A second NOR gate then takes A and P to yield Q=¬(A∨P)=¬A∧BQ = \lnot (A \lor P) = \lnot A \land B, while a third NOR gate takes B and P to yield R=¬(B∨P)=A∧¬BR = \lnot (B \lor P) = A \land \lnot B. A fourth NOR gate combines Q and R to produce S=¬(Q∨R)=¬((¬A∧B)∨(A∧¬B))=A⊙BS = \lnot (Q \lor R) = \lnot ((\lnot A \land B) \lor (A \land \lnot B)) = A \odot B, the XNOR output. Finally, a fifth NOR gate inverts S by feeding it to both inputs, yielding the XOR output ¬S=A⊕B\lnot S = A \oplus B. This NOR-based XOR circuit matches the standard truth table:
ABA ⊕ B
000
011
101
110
The output is 1 precisely when the inputs differ, verifying the parity-sensitive behavior. The , the complement of XOR, produces an output of 1 when inputs are identical and can be constructed using four 2-input by using the intermediate S signal from the above XOR circuit as the output. Alternatively, adding a NOT (implemented as a self-NOR) to the full XOR circuit requires six NOR gates total for XNOR. The four-NOR for XNOR is thus more direct than extending the XOR build. XOR realizations with NOR gates are less efficient than equivalent NAND-based designs, which require only four gates, but remain feasible owing to NOR's .

Applications and History

Digital Circuit Design

NOR logic plays a significant role in combinational circuits, where entire systems like s and decoders can be constructed using only NOR gates, simplifying fabrication processes in certain technologies by reducing the variety of gate types required. This universality allows for streamlined manufacturing in fabs focused on NOR-based designs, as all logic functions can be realized from a single gate type, minimizing production complexity and potential defects. For instance, a 2-to-1 can be implemented with a network of NOR gates by expressing the selection logic in product-of-sums form, which naturally suits NOR realization. In sequential applications, NOR gates form the basis of fundamental memory elements, such as the SR constructed from two cross-coupled NOR gates. This configuration provides set and reset inputs that control the output state: when the set input is active (high) and reset low, the output goes high and holds that state until reset is activated; conversely, reset active sets the output low, demonstrating bistable behavior essential for flip-flops and registers in digital systems. The cross-coupling ensures the retains its state without continuous input, making it a core building block for with inherent reliability in state preservation. Modern applications leverage NOR logic in , notably NOR flash, where the parallel architecture enables reads across multiple bits simultaneously, supporting fast code execution and execute-in-place operations in embedded systems like automotive and industrial controllers. This parallel read capability contrasts with serial structures in other memories, providing low-latency access critical for boot processes and real-time applications. Additionally, NOR gates offer advantages in low-power VLSI designs, particularly at ultra-low voltages, where optimized NOR structures achieve high speed with reduced energy consumption compared to multi-gate alternatives. Design trade-offs with NOR logic include fan-in limitations due to series-connected PMOS transistors in implementations, typically restricting practical to 3 or 4 inputs to avoid excessive delay from stacked resistances. However, these gates excel in programmable logic arrays (PLAs), where NOR-based planes efficiently implement sum-of-products expressions through dynamic NOR arrays in both AND and OR sections, enabling flexible logic realization with minimal static power. A notable historical example is the use of integrated circuits, such as the Fairchild 9915 dual 3-input NOR, in the , where thousands of such gates ensured high reliability in the harsh space environment through redundant, universal logic construction.

Historical Development

The logical NOR operation traces its origins to the late , when American philosopher and logician introduced the concept of joint denial, symbolized by the Peirce arrow (↓), in his 1880 paper "On the Algebra of Logic." Peirce demonstrated that this single operation could serve as a universal primitive for expressing all possible functions, a key insight into the functional completeness of NOR that predated its electronic implementation by decades. This theoretical foundation highlighted NOR's potential for simplifying logical systems, influencing later work on switching theory. The practical realization of NOR logic advanced significantly in the through . In his seminal 1938 master's thesis, "A Symbolic Analysis of Relay and Switching Circuits," applied to the design of electromechanical networks, explicitly showing how NOR functions could be implemented using relays as switches—bridging abstract logic to tangible . Early computers like (1945) employed vacuum tube-based logic gates, including NOR configurations, to perform computations, though these were bulky and power-intensive. The transistor's invention in 1947 at enabled more efficient semiconductor realizations, shifting from tubes to solid-state devices. A pivotal milestone occurred in 1958 when at demonstrated the first , a germanium-based that integrated multiple components on a single chip, facilitating the miniaturization of logic gates like NOR. By 1961, commercial integrated NOR gates emerged, initially in resistor-transistor logic (RTL) form, powering aerospace systems such as the Minuteman missile guidance and the , which relied on thousands of 3-input NOR ICs from and Fairchild. The 1960s saw the rise of transistor-transistor logic (TTL) NOR gates, standardized by and widely adopted in minicomputers like the PDP-8, due to their speed and reliability. NOR logic evolved further with in the 1970s. The , the world's first single-chip released in 1971, utilized p-channel MOS (PMOS) circuitry heavily based on NOR gates for its control and arithmetic functions, marking NOR's integration into programmable computing. By the late 1970s and 1980s, complementary (CMOS) NOR gates dominated microprocessors like the , offering low power consumption and high density. A major innovation came in 1984 when Fujio Masuoka at presented NOR at the IEEE International Electron Devices Meeting, a non-volatile storage architecture using NOR gates for parallel access, with foundational patents filed earlier in the decade. This development propelled NOR into , evolving from to embedded memory in modern devices.

References

  1. https://dc.etsu.edu/cgi/viewcontent.cgi?filename=0&article=1031&context=computer-organization-design-oer&type=additional
  2. http://class.ece.iastate.edu/ee508/GAS_book/chap7b.pdf
  3. https://engineering.purdue.edu/~meyer/DDU270/Refs/Pld/pal_guide.pdf
  4. https://www.ece.lsu.edu/alex/EE2720/EE2720_HO9.pdf
  5. https://dspace.mit.edu/handle/1721.1/11173
  6. https://userpages.cs.umbc.edu/chang/cs313/topics/Slides19.pdf
  7. https://www.techtarget.com/whatis/definition/logic-gate-AND-OR-XOR-NOT-NAND-NOR-and-XNOR
  8. https://www.electronics-tutorials.ws/logic/logic_6.html
  9. https://www.electrical4u.com/nor-gate/
  10. https://www.geeksforgeeks.org/digital-logic/nor-gate/
  11. https://www.electricaltechnology.org/2018/04/digital-logic-nor-gate.html
  12. https://standards.ieee.org/ieee/91_91a/241/
  13. https://commons.wikimedia.org/wiki/File:Logic-gate-nor-iec.png
  14. https://www.ic-components.com/blog/comparing-the-design-and-application-of-mil-std-806b-and-iec-60617-logic-gate-symbols.jsp
  15. https://eepower.com/technical-articles/basic-cmos-logic-gates/
  16. https://www.allaboutcircuits.com/textbook/digital/chpt-3/ttl-nor-and-or-gates/
  17. https://www.ti.com/lit/ml/sdyz001a/sdyz001a.pdf
  18. https://lecture-notes.tiu.edu.iq/wp-content/uploads/2022/03/Ch3-Thomas_L._Floyd.pdf
  19. http://homepage.divms.uiowa.edu/~ghosh/9-26-13.pdf
  20. https://web.eecs.utk.edu/~mbeck/classes/cs160/lectures/04_gates_boolean.pdf
  21. http://faculty.etsu.edu/tarnoff/ntes2150/balgebra/balgebra.htm
  22. https://courses.cs.washington.edu/courses/cse370/10wi/pdfs/lectures/04-CanonicalForms.pdf
  23. https://cs.wellesley.edu/~cs240/s23/slides/gates.pdf
  24. https://www.nku.edu/~longa/classes/2003fall/mat385/days/day22/Handout3.pdf
  25. https://www.csie.ntu.edu.tw/~lyuu/complexity/2016/20161011.pdf
  26. http://homepage.divms.uiowa.edu/~ghosh/6016.5.pdf
  27. https://www.sfu.ca/~jeffpell/papers/PostPellMartin.pdf
  28. https://engineering.purdue.edu/~heller/ABE565/Lecture%2020%20CMOS%20Logic%20Gates.pdf
  29. https://www.ti.com/lit/ds/symlink/sn7400.pdf
  30. https://www.ti.com/lit/ds/symlink/sn7402.pdf
  31. https://www.tutorialspoint.com/digital-electronics/implementation-of-not-gate-from-nor-gate.htm
  32. https://www.tutorialspoint.com/digital-electronics/implementation-of-or-gate-from-nor-gate.htm
  33. https://www.tutorialspoint.com/digital-electronics/implementation-of-and-gate-from-nor-gate.htm
  34. https://www.allaboutcircuits.com/textbook/digital/chpt-3/gate-universality/
  35. https://www.allaboutcircuits.com/textbook/digital/chpt-7/demorgans-theorems/
  36. https://www.electronics-tutorials.ws/logic/logic_5.html
  37. https://www.allaboutcircuits.com/textbook/digital/chpt-3/multiple-input-gates/
  38. https://www.tutorialspoint.com/digital-electronics/implementation-of-xnor-gate-from-nor-gate.htm
  39. https://www.geeksforgeeks.org/digital-logic/xor-gate/
  40. https://electronics.stackexchange.com/questions/57213/what-is-the-minimum-number-of-nor-gates-needed-to-implement-a-2-input-multiplexe
  41. https://www.electronics-tutorials.ws/sequential/seq_1.html
  42. https://www.micron.com/products/nor-flash
  43. https://www.thinkmind.org/articles/cenics_2012_1_20_70048.pdf
  44. https://pages.hmc.edu/harris/class/e158/01/lect10.pdf
  45. https://ieeexplore.ieee.org/document/4787564
  46. https://www.eejournal.com/article/the-first-ics-on-the-moon-the-apollo-guidance-computer-part-2/
  47. https://www.cs.virginia.edu/~evans/greatworks/shannon38.pdf
  48. https://www.nobelprize.org/prizes/physics/2000/kilby/facts/
  49. https://www.computerhistory.org/siliconengine/aerospace-systems-are-first-the-applications-for-ics-in-computers/
  50. https://www.computerhistory.org/siliconengine/standard-logic-ic-families-introduced/
  51. https://spectrum.ieee.org/moores-law-milestones
Add your contribution
Related Hubs
User Avatar
No comments yet.