Community hub
0 subscribers8 pages, 0 posts
Recent from talks
Be the first to start a discussion here.
Be the first to start a discussion here.
Be the first to start a discussion here.
Be the first to start a discussion here.
Contribute something
Welcome to the community hub built to collect knowledge and have discussions related to Band-stop filter.
Nothing was collected or created yet.
Band-stop filter
View on Wikipediafrom Wikipedia
 | This article needs additional citations for verification. (June 2010) |
In signal processing, a band-stop filter or band-rejection filter is a filter that passes most frequencies unaltered, but attenuates those in a specific range to very low levels.[1] It is the inverse of a band-pass filter. A notch filter is a band-stop filter with a narrow stopband (high Q factor).
Narrow notch filters (optical) are used in Raman spectroscopy, live sound reproduction (public address systems, or PA systems) and in instrument amplifiers (especially amplifiers or preamplifiers for acoustic instruments such as acoustic guitar, mandolin, bass instrument amplifier, etc.) to reduce or prevent audio feedback, while having little noticeable effect on the rest of the frequency spectrum (electronic or software filters). Other names include "band limit filter", "T-notch filter", "band-elimination filter", and "band-reject filter".
Typically, the width of the stopband is 1 to 2 decades (that is, the highest frequency attenuated is 10 to 100 times the lowest frequency attenuated). However, in the audio band, a notch filter has high and low frequencies that may be only semitones apart. From the figure of the frequency response of an ideal band-stop filter, it's obvious that the band-stop filter is simply an inverted band-pass filter where they share same definition of bandwidth, pass band, stop band and center frequency. The attenuation should be infinite in the stop band and be zero in the two pass bands for an ideal band-stop filter. Band-stop filters are designed by the combination of a low-pass filter and a high-pass filter in a parallel configuration. Overlapping does not occur in the summation of high-pass filter and low-pass filter during the design of band-stop filter. The difference in the starting and ending frequency points causes the two filters to connect effectively without any overlapping.
Mathematical description
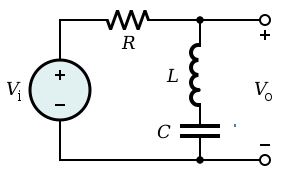
[edit]Band-stop filter can be represented as a combination of low-pass and high-pass filters if the bandwidth is wide enough that the two filters do not interact too much. A more general approach is to design as a low-pass prototype filter which can then be transformed into a bandstop. The simple notch filter shown can be directly analysed. The transfer function is,
Here is zero circular frequency and is the pole circular frequency. Zero frequency is the cutoff frequency and sets the type of the notch filter: standard notch when , low-pass notch () and high-pass notch () filters. denotes the Q-factor.[2]
For standard notch filter the formulation can be rewritten as
where is the central rejected frequency and is the width of the rejected band.
Examples
[edit]In the audio domain
[edit]- Anti-hum filter
For countries using 60 Hz power lines:
- low frequency: 59 Hz,
- middle frequency: 60 Hz,
- high frequency: 61 Hz.
This means that the filter passes all frequencies, except for the range of 59–61 Hz. This would be used to filter out the mains hum from the 60 Hz power line, though its higher harmonics could still be present.
For countries where power transmission is at 50 Hz, the filter would have a 49–51 Hz range.
In the radio-frequency (RF) domain
[edit]- Non-linearities of power amplifiers
When measuring the non-linearities of power amplifiers, a very narrow notch filter can be very useful to avoid the carrier frequency. Use of the filter may ensure that the maximum input power of a spectrum analyser used to detect spurious content will not be exceeded.
- Wave trap
A notch filter, usually a simple LC circuit, is used to remove a specific interfering frequency. This is a technique used with radio receivers that are so close to a transmitter that it swamps all other signals. The wave trap is used to remove or greatly reduce the signal from the nearby transmitter.[3]
- Software-defined radio
Most affordable software-defined radios (SDR) on the market today suffer from limited dynamic and operating ranges. In other words, in real-world operating environments, a SDR can easily be saturated by a strong signal. In particular FM broadcast signals are very strong and nearly everywhere. These signals can prevent a SDR from processing other weak signals. FM notch filters are very useful for SDR applications and have increased in their popularity.
Optical filtering (wavelength selection)
[edit]In optics, there are several methods of filtering selected wavelengths from a source or to a detector. They rely on scattering or destructive interference.
Filtering by scattering and diffraction
[edit]A diffraction grating[4] or a dispersive prism may be used to selectively redirect selected wavelengths of light within an optical system.
In the case of transmission gratings and prisms, polychromatic light that passes through the object will be redirected according to wavelength. A slit may then be used to select wavelengths that are desired. A reflective grating may also be utilized for the same purpose, though in this case light is reflected rather than transmitted. Filters of this design may be high-pass, band-pass, or low-pass, depending on system configuration.
Filtering by interference
[edit]When using optics with real materials, light will be attenuated at various wavelengths through interference with the medium through which the light traversed. In this sense, material selection may be utilized to selectively filter light according to the wavelengths that are minimally attenuated. To some extent, all real optical systems will suffer from this phenomenon.
Alternatively, it is also possible to use an oscillating reflecting surface to cause destructive interference with reflected light along a single optical path. This principle is the basis for a Michelson interferometer.
Band-stop smoothing filter
[edit]Smoothing filter is essential in many fields, such as signal and image processing, computer vision, statistics, stated by Roonizi (2021).[5] Algorithms such as quadratic variation regularization and smoothness priors are the most common way to perform signal denoising. These algorithms are implemented to band-stop smoothing filters and being investigated by Roonizi (2021).[5] A naive band-stop smoothing filter is raised, which is constructed by connecting a high-pass smoothing filter and a low-pass smoothing filter. These two smoothing filter sections are configured in parallel way. Moreover, it was suggested that positive noise correlation promises to obtain the best band-stop smoothing filter.
Telecommunications
[edit]The development of telecommunications applications raises the demand of radio frequency and microwave filters, stated by Haddi (2019).[6] Those filters are commonly used in PA systems (Public Address Systems) and speaker systems to produce audio with great quality. Microwave filters have high flexibility of actualization and low cost. The band-stop filter in the telecommunications field, has a respectable place which it is essential for microwave transceivers. For example, wireless communication systems make use of band-stop filters to achieve the requirement of miniaturization.
Microstrip Band-stop Filter
[edit]Microstrip-line band-stop filter is convenient to implement with low cost and light weight. Hsieh & Wang (2005) stated that, conventional microstrip band-stop filters are made of shunt open-circuited resonators.[7] They usually has the characteristic of having narrow stopband. However, alternating the band-stop filter to have a wide stop band response with specific design can bring huge advantage over the conventional band-stop filters.
The advantages of the microstrip band-stop filter designed by Hsieh & Wang (2005) is its compact size and easy implementation. This improved band-stop filter with wide stop-band has additional amount of transmission zeros. The purpose of this design is to combine a shunt open-circuited quarter-wavelength resonator with one section of quarter-wavelength frequency-selecting coupling structure, stated by Hsieh & Wang (2005). As a result, a simple structured band-stop filter with easy implementation can bring advantages of lower-order resonators, great stop band performance when compared to conventional microstrip band-stop filters.
See also
[edit]References
[edit]- ^ "Band-stop filter", Federal Standard 1037C, accessed 14 May 2018.
- ^ "Chapter 8: Analog Filters". Basic Linear Design. USA: Analog Devices Inc. 2006.
- ^ Carr, Joseph J. (2001). The technician's radio receiver handbook: Wireless and telecommunication technology, p. 282. Newnes. ISBN 0-7506-7319-2.
- ^ Terracciano, Anthony (2018). "Hazardous Gas Detection Sensor Using Broadband Light-Emitting Diode-Based Absorption Spectroscopy for Space Applications". New Space. 6 (1): 28–36. Bibcode:2018NewSp...6...28T. doi:10.1089/space.2017.0044. OSTI 1435270.
- ^ a b Roonizi, Arman Kheirati; Jutten, Christian (2021). "Band-Stop Smoothing Filter Design". IEEE Transactions on Signal Processing. 69: 1797–1810. Bibcode:2021ITSP...69.1797R. doi:10.1109/TSP.2021.3060619. ISSN 1941-0476. S2CID 233137801.
- ^ Haddi, Souhaila Ben; Zugari, Asmaa; Zakriti, Alia; Achraou, Soufiane (2020-01-01). "Design of a Band-Stop Planar Filter for Telecommunications Applications". Procedia Manufacturing. 46: 788–792. doi:10.1016/j.promfg.2020.04.006. ISSN 2351-9789. S2CID 219444573.
- ^ Hsieh, Ming-Yu; Wang, Shih-Ming (July 2005). "Compact and wideband microstrip bandstop filter". IEEE Microwave and Wireless Components Letters. 15 (7): 472–474. Bibcode:2005IMWCL..15..472H. doi:10.1109/LMWC.2005.851572. ISSN 1558-1764.
Wikimedia Commons has media related to Band-reject filters.
Band-stop filter
View on Grokipediafrom Grokipedia
A band-stop filter, also known as a band-rejection or notch filter, is an electronic filter that attenuates signals within a specific frequency range, known as the stopband, while allowing frequencies below and above that range to pass through with minimal distortion.[1] This contrasts with band-pass filters, which instead emphasize a particular frequency band. The filter's performance is characterized by its center frequency, bandwidth (the width of the stopband, typically defined between -3 dB points), and quality factor (Q), which indicates the sharpness of the rejection.[1]
Band-stop filters can be implemented as passive circuits using resistors, capacitors, and inductors, or as active circuits incorporating operational amplifiers for improved selectivity and gain.[1] A common passive design is the twin-T network, which provides deep attenuation at a narrow stopband, while active versions often combine low-pass and high-pass sections in parallel to achieve the rejection effect.[1] In digital signal processing, band-stop filters are realized through algorithms like finite impulse response (FIR) or infinite impulse response (IIR) structures, enabling precise control in software-defined systems.[2]
These filters find widespread applications in electronics and communications for suppressing interference, such as eliminating 50/60 Hz power-line hum in audio systems or rejecting specific carrier frequencies in radio transmissions.[1] In signal processing, they reduce noise by targeting unwanted frequency components, enhancing clarity in telecommunications and instrumentation. Advanced uses include radar and electronic warfare systems for co-site interference mitigation, as well as acoustic engineering to block resonant frequencies in architectural designs.[3][4]
Fundamentals
Definition and Characteristics
A band-stop filter, also known as a notch filter or band-rejection filter, is an electronic filter that attenuates frequencies within a specific range while allowing most other frequencies to pass through with minimal alteration.[1][5] This design is essential for eliminating unwanted signals in a narrow or defined spectral band without significantly impacting the overall signal integrity.[6] Key characteristics of a band-stop filter include its center frequency, which marks the midpoint of the attenuated band where rejection is maximum; bandwidth, typically defined as the 3 dB bandwidth between the upper and lower cutoff frequencies where the signal is attenuated by 3 dB; quality factor (Q), calculated as the ratio of the center frequency to the bandwidth, indicating the filter's selectivity and sharpness; and stopband attenuation depth, which measures the maximum rejection level in decibels within the stopband.[1][6] Higher Q values correspond to narrower bandwidths and steeper transitions, enhancing precision in frequency rejection.[7] In a basic block diagram, a band-stop filter consists of an input port receiving the signal, a filtering network that performs the attenuation, and an output port delivering the processed signal; this can be implemented using passive components like resistors, capacitors, and inductors or active elements such as operational amplifiers for improved performance.[1] Ideally, the filter provides infinite attenuation across the entire stopband with zero insertion loss in the passbands and infinitely sharp transitions at the edges; however, real-world implementations exhibit finite attenuation depths, gradual roll-off slopes outside the stopband, and some insertion loss due to component imperfections and parasitic effects.[1][6] A band-stop filter operates as the complementary inverse to a band-pass filter, rejecting rather than passing a targeted frequency band.[5]Comparison to Other Filters
Band-stop filters serve as the complementary counterpart to band-pass filters in the frequency domain, where a band-stop filter attenuates signals within a specific frequency band while allowing frequencies outside that band to pass through, whereas a band-pass filter does the opposite by passing only the targeted band and rejecting others.[8] This inverse relationship makes band-stop filters particularly useful for eliminating narrowband interference without broadly affecting the desired signal spectrum.[9] In contrast to low-pass and high-pass filters, which rely on a single cutoff frequency to separate broad spectral regions—low-pass attenuating above the cutoff and high-pass below—band-stop filters target a narrower rejection band by effectively combining elements of both, but with a focus on a defined stopband rather than indefinite roll-off beyond cutoffs.[9] This allows band-stop filters to provide a broader notch for interference suppression compared to the cutoff-based attenuation of low- or high-pass designs, which are better suited for removing entire high- or low-frequency content.[8] Unlike all-pass filters, which maintain constant amplitude response across all frequencies and solely modify phase for applications like delay or equalization, band-stop filters actively alter amplitude by attenuating within the stopband, introducing no such phase-only behavior.[9] The choice of a band-stop filter is often driven by the need for targeted interference removal, such as eliminating 60 Hz power line hum in audio or instrumentation systems, whereas band-pass filters are preferred for isolating specific signal bands, like in channel selection for telecommunications.[9] Low- and high-pass filters excel in general noise reduction across wide ranges, but lack the precision for narrowband rejection without excessive signal distortion.[8]| Filter Type | Response Shape | Complexity | Typical Q Values |
|---|---|---|---|
| Low-Pass | Passes below cutoff; attenuates above | Simple (e.g., RC networks) | ~0.71 (2nd-order Butterworth)[9] |
| High-Pass | Passes above cutoff; attenuates below | Simple to moderate | ~0.71 (2nd-order Butterworth)[9] |
| Band-Pass | Passes narrow band; attenuates outside | Moderate to high | 1 to 10[9] |
| Band-Stop | Attenuates narrow band; passes outside | Moderate (e.g., twin-T) | 0.25 (passive) to 10 (active)[9] |
| All-Pass | Constant amplitude; phase shift only | Moderate | Not applicable (phase/delay focused)[9] |
Mathematical Theory
Transfer Function and Equations
The transfer function of a second-order analog band-stop filter, often referred to as a notch filter prototype, is given by where is the gain factor (typically 1 for unity passband gain), is the center (notch) angular frequency, and is the quality factor determining the stopband width.[10] This form ensures attenuation at while passing low and high frequencies. This transfer function can be derived from an RLC circuit configuration, such as a series RLC shunt to ground with the output across the resistor. For a parallel RLC band-stop filter, the impedance of the LC tank is infinite at resonance (), leading to zero output voltage; applying voltage division yields the numerator from the LC branch and the denominator incorporating damping via , resulting in the term.[11] Similarly, a series RLC configuration in the signal path produces a zero impedance at resonance, attenuating the signal and deriving the same functional form through Kirchhoff's laws.[11] In the s-plane, the pole-zero placement features zeros at on the imaginary axis, creating the notch, while the poles lie in the left half-plane at for stability and to shape the roll-off.[10] Higher-order band-stop filters cascade multiple such second-order sections, with poles positioned to meet stopband attenuation requirements. To obtain band-stop filters from a normalized low-pass prototype (with cutoff at 1 rad/s), apply the frequency transformation , where is the stopband bandwidth and with as the band edges.[12] This substitution maps the low-pass response to reject frequencies around while preserving passbands, doubling the order (e.g., second-order low-pass becomes fourth-order band-stop). For digital implementation, infinite impulse response (IIR) band-stop filters are designed by first obtaining the analog prototype and applying the bilinear transform , where is the sampling period, to yield .[13] Pre-warping the frequencies () ensures accurate digital mapping; substituting into the analog produces a rational for second-order, with coefficients computed to match the analog poles and zeros.[13] This method preserves stability if the analog filter is stable.[13]Frequency Response Analysis
The frequency response of a band-stop filter is characterized by its magnitude response, which approximates unity gain (|H(jω)| ≈ 1) in the passbands below the lower cutoff frequency and above the upper cutoff frequency, while exhibiting a deep attenuation or null within the stopband centered at the notch frequency ω₀. This null provides near-complete rejection at ω₀, with the depth and width of the stopband determined by the filter's quality factor Q; higher Q values result in a narrower, sharper rejection band, enhancing selectivity but potentially introducing greater distortion near the edges.[10][1] In Bode plot representations, the magnitude response in decibels shows flat 0 dB levels in the passbands, transitioning into the stopband with roll-off rates that reflect the filter order—for a second-order band-stop filter, this is typically 20 dB per decade as the response drops toward the minimum attenuation at ω₀ before rising symmetrically back to 0 dB. The phase response exhibits a characteristic shift around the stopband, often approaching 180 degrees of total variation for second-order designs, which arises from the poles and zeros in the transfer function.[10][14] Group delay in band-stop filters tends to peak near the stopband edges, with variations increasing for higher-order or higher-Q designs due to the sharper transitions; this can lead to signal distortion if not minimized, particularly in applications requiring linear phase. Passband ripple is generally minimal in well-designed filters, such as those approximating Butterworth characteristics, though elliptic designs may introduce controlled ripple for steeper roll-off at the expense of delay uniformity. The impact of Q on sharpness is evident in the stopband bandwidth, defined as BW = ω₀ / Q, where larger Q narrows the BW, improving rejection precision but amplifying group delay peaks.[10][3] Stability analysis for analog band-stop filters relies on the Nyquist stability criterion, ensuring the Nyquist plot of the open-loop transfer function encircles the -1 point an appropriate number of times based on right-half-plane poles, with all closed-loop poles required to lie in the left half of the s-plane. For digital implementations, stability demands that all poles lie inside the unit circle in the z-plane to prevent unbounded responses.[10][15] As an example, for a second-order active notch filter with Q = 10 centered at 1 kHz, the attenuation at the notch frequency can achieve approximately 40 dB, demonstrating effective rejection while maintaining passband integrity, as verified in practical op-amp-based designs.[1]Design Principles
Analog Design Methods
Analog band-stop filters, also known as notch filters, are synthesized using passive or active components to attenuate a specific frequency band while passing others, leveraging principles from transfer function analysis such as pole-zero placement where zeros are positioned at the notch frequency and poles define the roll-off.[10] Passive designs commonly employ the Twin-T or parallel-T topology, consisting of two T-shaped networks formed by resistors (R) and capacitors (C) arranged in a bridged configuration to create a null at the desired center frequency. In this setup, the notch frequency is determined by , allowing component values to be selected such that for equal RC pairs, which yields a fixed quality factor and a bandwidth . For example, to achieve a 60 Hz notch, values like and provide infinite rejection at , though practical attenuation is limited to about 40-60 dB with standard components due to parasitic effects.[16][10] Active designs enhance performance using operational amplifiers (op-amps) to realize topologies like the inverted Sallen-Key or bootstrapped Twin-T, eliminating the need for inductors and enabling higher Q factors through feedback. The Sallen-Key band-stop variant inverts the standard low-pass configuration by incorporating a parallel RC network in the feedback path, with the transfer function where and Q is tuned via gain adjustments without shifting the mid-frequency, offering advantages in tunability for applications below 10 MHz and reduced sensitivity compared to passive LC circuits.[9][10] For higher-order filters, Butterworth and Chebyshev approximations are adapted to band-stop responses via frequency transformations, such as replacing with in low-pass prototypes, where is the bandwidth and poles are placed using normalized tables for orders greater than 2 to achieve maximally flat or equiripple stop-band characteristics. Butterworth designs position poles on a unit circle in the s-plane for monotonic response, while Chebyshev uses elliptic pole loci with specified ripple (e.g., 0.5 dB) for steeper transitions, as in a 3-pole example with stage frequencies at 763.7 Hz, 1000 Hz, and 1309 Hz and Q values of 6.54 and 1.07.[10] Sensitivity analysis reveals that component tolerances significantly impact Q, particularly in high-Q sections; for instance, the Twin-T topology exhibits high sensitivity where a 1% variation in R or C can degrade Q by up to 25%, limiting practical notches to 60 dB with 1% components, while active designs like state-variable structures mitigate this through lower pole-Q sensitivity. In LC-based passive band-stop filters, inductor losses introduce parasitic resistance that reduces Q at high frequencies (above 1 MHz), imposing practical limits such as increased insertion loss and broadened stop-band, often necessitating active alternatives for precision.[10][17][18] The development of analog band-stop filters traces to the 1950s and 1960s, building on Hendrik Bode's foundational work in network synthesis and feedback for precise frequency control, with early active notch designs emerging alongside op-amp advancements to enable tunable rejection without bulky inductors.[19][10]Digital Design Methods
Digital band-stop filters, also known as notch filters when narrowband, are designed in the discrete-time domain to attenuate a specific frequency band while passing others, often transforming analog prototypes or directly specifying digital responses.[20] These designs leverage sampled data processing, contrasting with continuous analog methods by incorporating discretization effects like aliasing considerations.[21] Infinite impulse response (IIR) digital band-stop filters are commonly derived from analog prototypes using the bilinear transform, which maps the s-plane to the z-plane via , where is the sampling period, preserving stability for causal filters.[22] To ensure accuracy at the stopband center frequency , pre-warping is applied by adjusting the analog frequency specification to , compensating for the nonlinear frequency mapping introduced by the transform.[22] This method yields efficient filters with sharp transitions but potential phase nonlinearity.[23] Finite impulse response (FIR) digital band-stop filters achieve linear phase by symmetry in coefficients, often designed via the window method applied to the inverse discrete-time Fourier transform (IDTFT) of an ideal band-stop frequency response.[24] The ideal impulse response is obtained through inverse FFT of a rectangular frequency response (unity in passbands, zero in stopband), then windowed (e.g., Hamming or Kaiser) to truncate and reduce Gibbs ripple; longer filter lengths (higher order) enable sharper stopband edges but increase computational cost.[25] Trade-offs include broader transition bands for shorter lengths versus higher latency and resources for sharper notches.[26] In digital signal processing (DSP) implementations, band-stop filters operate via difference equations, such as the general IIR form , where coefficients define the response; for band-stop, these are computed using functions like MATLAB'sbutter(N, Wn, 'stop') for Butterworth prototypes.[27] Equivalent tools in Octave provide similar coefficient generation for real-time execution.[28]
Quantization effects arise in hardware realizations, with fixed-point arithmetic introducing coefficient and round-off noise that can degrade stopband attenuation, particularly in recursive IIR structures prone to limit cycles, whereas floating-point offers higher dynamic range and precision at greater computational expense.[29] Aliasing is prevented by ensuring the sampling rate exceeds twice the highest frequency of interest, per the Nyquist criterion, often augmented by digital pre-filters.[21]
Modern software tools facilitate design, such as Python's SciPy signal.butter(N, Wn, btype='bandstop', output='ba', fs=fs) introduced in the early 2000s, which generates coefficients for both IIR and FIR variants and supports real-time deployment in embedded systems like microcontrollers via optimized libraries.[30]