Hubbry Logo
Astronomical ringsAstronomical ringsMain
Open search
Astronomical rings
Community hub
Astronomical rings
logo
8 pages, 0 posts
0 subscribers
Be the first to start a discussion here.
Be the first to start a discussion here.
Astronomical rings
Astronomical rings
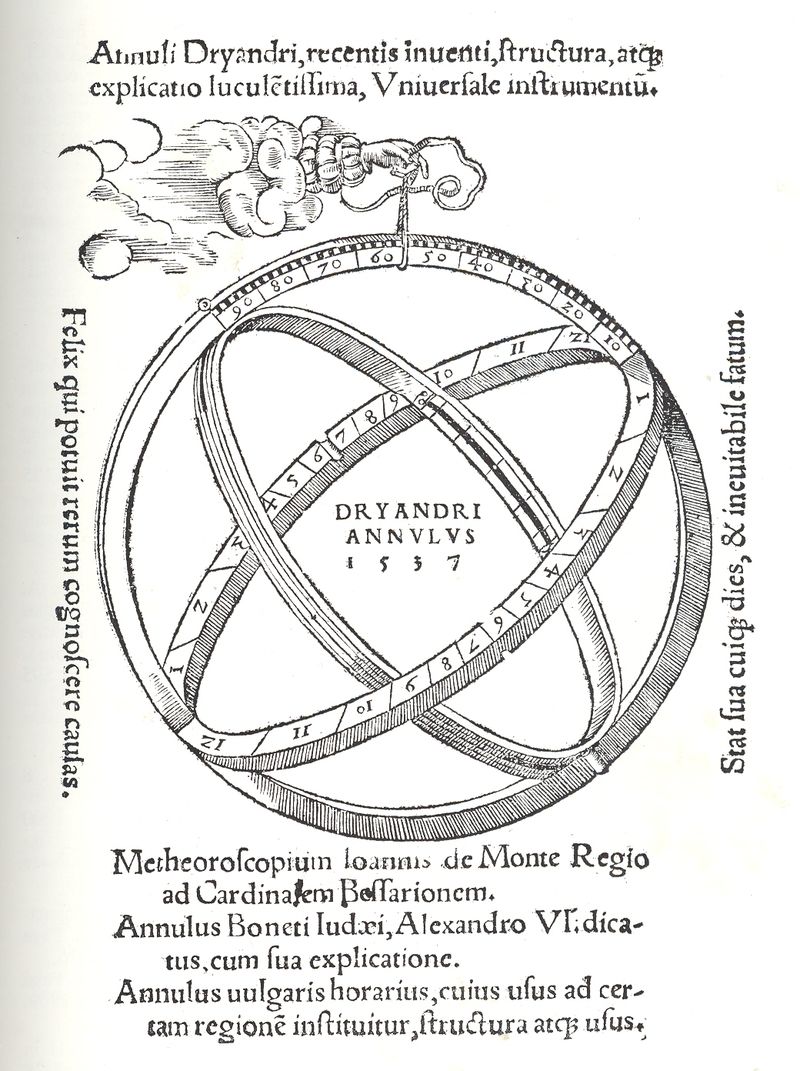
Astronomical rings
View on Wikipedia
from Wikipedia
Diagram of astronomical rings (Johannes Dryander, Annulorum trium diversi generis..., published Marburg, 1537)

Astronomical rings (Latin: annuli astronomici),[1] also known as Gemma's rings, are an early astronomical instrument. The instrument consists of three rings, representing the celestial equator, declination, and the meridian.

It can be used as a sun dial to tell time, if the approximate latitude and season is known, or to tell latitude, if the time is known or observed (at solar noon). It may be considered to be a simplified, portable armillary sphere, or a more complex form of astrolabe.

History

[edit]

Parts of the instrument go back to instruments made and used by ancient Greek astronomers. Gemma Frisius combined several of the instruments into a small, portable, astronomical-ring instrument. He first published the design in 1534,[2] and in Petrus Apianus's Cosmographia in 1539. These ring instruments combined terrestrial and celestial calculations.[3]

Types

[edit]

Fixed astronomical rings

[edit]
Equinoctal sun dial

Fixed astronomical rings are mounted on a plinth, like armillary spheres, and can be used as sundials.

Traveller's sundial or universal equinoctal ring dial

[edit]

The dial is suspended from a cord or chain; the suspension point on the vertical meridian ring can be changed to match the local latitude. The time is read off on the equatorial ring; in the example below, the center bar is twisted until a sunray passes through a small hole and falls on the horizontal equatorial ring.

Sun ring

[edit]

A sunring or farmer's ring is a latitude-specific simplification of astronomical rings. On one-piece sunrings, the time and month scale is marked on the inside of the ring; a sunbeam passing through a hole in the ring lights a point on this scale. Newer sunrings are often made in two parts, one of which slides to set the month; they are usually less accurate.

  • Diagram of a one-part sunring, with sunbeam
    Diagram of a one-part sunring, with sunbeam
  • A two-part sunring or farmer's ring, with light beam showing the time
    A two-part sunring or farmer's ring, with light beam showing the time
  • A simpler sundial ring, not in use
    A simpler sundial ring, not in use

Sea ring

[edit]
Modern sundial compass

In 1610, Edward Wright created the sea ring, which mounted a universal ring dial over a magnetic compass. This permitted mariners to determine the time and magnetic variation in a single step.[4] These are also called "sundial compasses".

Structure and function

[edit]

The three rings are oriented with respect to the local meridian, the planet's equator, and a celestial object. The instrument itself can be used as a plumb bob to align it with the vertical. The instrument is then rotated until a single light beam passes through two points on the instrument. This fixes the orientation of the instrument in all three axes.

The angle between the vertical and the light beam gives the solar elevation. The solar elevation is a function of latitude, time of day, and season. Any one of these variables can be determined using astronomical rings, if the other two are known.

The altitude of the sun does not change much in a single day at the poles (where the sun rises and sets once a year), so rough measurements of solar altitude don't vary with time of day at high latitudes.

Use as a calendar sundial

[edit]

When the solar time is exactly noon, or known from another clock, the instrument can be used to determine the time of year.

The meridional ring can function as the gnomon, when the rings are used as a sundial. A horizontal line aligned on a meridian with a gnomon facing the noon-sun is termed a meridian line and does not indicate the time, but instead the day of the year. Historically they were used to accurately determine the length of the solar year. A fixed meridional ring on its own can be used as an analemma calendar sundial, which can be read only at noon.

When the shadow of the rings are aligned so that they appear to be in the same, or nearly the same, place, the meridian identifies itself.[clarification needed]

Meridional ring

[edit]

The meridian ring is placed vertically, then rotated (relative to the celestial object) until it is parallel to the local north-south line. The whole ring is thus parallel to the circle of longitude passing through the place where the user is standing.

Because the instrument is often supported by the meridional ring, it is often the outermost ring, as it is in the traveller's rings illustrated above. There, a sliding suspension shackle is attached to the top of the meridional ring, from which the whole device can be suspended. The meridional ring is marked in degrees of latitude (0–90, for each hemisphere). When properly used, the pointer on the support points to the latitude of the instrument's location. This tilts the equatorial ring so that it lies at the same angle to the vertical as the local equator.[5][6]

Equatorial ring

[edit]

The equatorial ring occupies a plane parallel to the celestial equator, at right angles to the meridian. It is aligned by

  • being attached to the meridional ring at the marking for latitude zero (see above)
  • being aligned to the declension ring, which is aligned to the celestial object.

Often equipped with a graduated scale, it can be used to measure right ascension. On the traveller's sundial shown above, it is the inner ring.

This ring is sometimes engraved with the months on one side and corresponding zodiac signs on the outside; very similar to an astrolabe. Others have been found to be engraved with two twelve-hour time scales. Each twelve-hour scale is stretched over 180 degrees and numbered by hour with hashes every 20 minutes and smaller hashes every four minutes. The inside displays a calendrical scale with the names of the months indicated by their first letters, with a mark to show every 5 days and other marks to represent single days. On these, the outside of the ring is engraved with the corresponding symbols of the zodiac signs. The position of the symbol indicates the date of the entry of the sun into this particular sign. The vernal equinox is marked at March 15 and the autumnal equinox is marked at September 10.[7]

Declination ring

[edit]
Astronomical ring with an alidade on the declination ring (folded closed).

The declination ring is moveable, and rotates on pivots set in the meridian ring. An imaginary line connecting these pivots is parallel to the Earth's axis. The declination "ring" of the traveller's sundial above is not a ring at all, but an oblong loop with a slider for setting the season.

This ring is often equipped with vanes and pinholes for use as the alidade of a dioptra (see image). It can be used to measure declination.

This ring is also often marked with the zodiac signs and twenty-five stars, similar to the astrolabe.

References

[edit]

Bibliography

[edit]
Revisions and contributorsEdit on WikipediaRead on Wikipedia

Astronomical rings

View on Grokipedia
from Grokipedia
Astronomical rings, also known as Gemma's rings (Latin: annuli astronomici), are a portable early modern astronomical instrument consisting of three interconnected brass rings that model key celestial coordinates: the equatorial ring for the , the meridian ring for the local meridian, and a third ring often serving as a horizon or circle with adjustable sights. Invented and first described by the Flemish mathematician, physician, and instrument maker Gemma Frisius in his 1534 Usus annuli astronomici, the device was designed for practical fieldwork without requiring fixed orientation tools like a . These rings gained popularity during the 16th-century , particularly in and the , where instrument makers like Gualterus Arsenius produced refined versions, often gilded and engraved with scales for hours, degrees (0–90°), zodiac signs, and even positions of 25 principal stars. Adjustable for latitudes typically between 42½° and 59° to suit European users, the instrument functioned as a multifunctional and : sunlight or a shadow cast through a small or onto the rings allowed users to determine local , calculate the sun's , measure the altitude of celestial objects, and perform basic surveying such as estimating heights of distant structures. Johann Dryander, a German physician and (1500–1560), further popularized and expanded on their design in his comprehensive 1537 treatise Annulorum trium diversi generis instrumentorum astronomicorum opus, which devoted significant sections to their construction, markings, and applications, establishing them as a bridge between and practical measurement. While precursors like the simpler annulus Boneti—a single-ring altitude measurer invented by the Jewish physician Bonet de Lattes in the late —existed, Gemma Frisius's version innovated by integrating multiple rings into a compact, foldable form ideal for travelers, navigators, and surveyors during the Age of Exploration. Surviving examples, such as an unsigned late-16th-century Flemish specimen in the (diameter 70 mm) and a 1567 signed dial by Arsenius in Oxford's of the History of Science, highlight their craftsmanship and enduring appeal as both scientific tools and ornamental objects. By the , astronomical rings influenced later portable instruments but faded as more precise tools like telescopes emerged, though their legacy persists in modern reproductions and studies of historical scientific instrumentation.

Overview

Definition and purpose

Astronomical rings, known in Latin as annulus astronomicus, are historical astronomical instruments consisting of three interconnected metal rings that represent key celestial coordinates, such as the equator, meridian, and horizon, functioning as a compact model of the celestial sphere. These devices, typically ranging from 2 to 6 inches in diameter and crafted from materials like brass or bronze, were designed for both fixed and portable use, allowing observers to align the rings with celestial bodies for measurements. The term annulus astronomicus derives from the Latin annulus, meaning "ring." The primary purposes of astronomical rings center on , enabling the measurement of the altitude of celestial bodies like the Sun or stars by sighting through aligned rings marked in degrees. They also facilitate determinations of by tracking the Sun's position relative to the meridian and season, as well as through adjustments to the observer's location and via zodiacal or monthly scales. These capabilities made the instruments valuable for practical applications, including at , , and computations to predict solar events. A key advantage of astronomical rings over larger armillary spheres lies in their compactness and portability, which allowed astronomers and navigators to conduct fieldwork without the encumbrance of bulkier models representing the full celestial sphere.

Key components

Astronomical rings are composed of three primary rings that model fundamental aspects of celestial geometry. The meridian ring serves as the outermost component, aligned parallel to the local meridian to establish north-south orientation and facilitate latitude determination through inscribed scales marked from 0 to 90 degrees in both directions. The equator ring is pivoted perpendicular to the meridian ring, representing the plane of the celestial equator and bearing a 12-hour scale divided into quarter-hours for temporal measurements, along with a calendrical scale featuring zodiac symbols. The declination ring, the innermost and most movable element, pivots around the polar axis to measure the angular distance of celestial bodies from the equator, equipped with an ecliptical scale and markings for select stars such as Arcturus and Spica. These rings interlock via hinged pivots and nested fittings, allowing the and meridian rings to be adjusted relative to each other to match the observer's , while the ring rotates freely for alignment with targeted objects. Additional features enhance precision and usability, including suspension vanes or pivots at the polar points for stable orientation during use, and sighting vanes—often in the form of a sliding ring with adjustable pinholes or slots—for sighting celestial bodies and projecting shadows or light beams onto the scales. Inscribed scales on all rings typically employ degree markings from 0 to 90 for altitude readings, with finer divisions into single degrees, and some include hour scales calibrated for time conversion based on solar position. Variations in labeling across instruments reflect adaptations for different observational needs, such as non-linear degree progressions on the ring to account for or zodiacal indicators for seasonal positioning, though core scales remain consistent in notation inherited from ancient astronomical traditions.

History

Ancient and medieval origins

The earliest concepts of astronomical rings trace back to the 2nd century BCE, when the Greek employed ring-like mechanisms in a four-ring sphere to measure stellar positions and celestial motions, building on Babylonian astronomical records and Egyptian shadow-casting tools for timekeeping. These instruments allowed for the determination of altitudes and azimuths by sighting through rings aligned with the and meridian. 's work laid foundational principles for , enabling precise observations of star declinations and , which influenced subsequent Greek and Roman designs. In the Roman era, documented adaptations of these ring-like dials in his (1st century BCE), describing simple annular dials for solar observations that used a ring suspended to cast shadows for time and seasonal measurements. These portable designs, attributed to earlier inventors like Dionysodorus, featured a graduated ring with a to track the sun's path, adapting Greek techniques for practical use in architecture and . emphasized their utility in varying latitudes, integrating them with gnomonic projections for local adjustments. Medieval Islamic scholars advanced ring designs significantly in the 9th–10th centuries, with refining meridian rings for accurate determination and orientation toward . 's Yamīnī ring, a large graduated instrument, incorporated degree scales for observing solar altitudes and lunar positions, essential for prayer times and geographical mapping in his Tahdīd nihāyāt al-amākin.

Renaissance and early modern developments

During the , astronomical rings underwent significant refinement, transitioning from medieval prototypes to more portable and versatile instruments suited for and . Johannes Regiomontanus (1436–1476), a pioneering German , contributed to early innovations by designing universal dials that allowed users to compute time and celestial positions without fixed orientation, making them ideal for travelers and influencing subsequent portable variants. In the 16th century, Regnier Gemma Frisius (1508–1555) played a pivotal role in popularizing astronomical rings through his detailed descriptions and practical applications. In his 1534 treatise Tractatus de annulo astronomico, Frisius outlined the instrument's three-ring structure—representing the horizon, meridian, and —for measuring , time, and stellar declinations, emphasizing its utility for seafarers in determining via accurate timing. His Louvain workshop, in collaboration with instrument-makers like Gualterus Arsenius, produced refined brass examples, such as a 1567 model for enhanced portability during voyages. These developments aligned with the era's exploratory demands, as rings were carried on ships to aid amid the Age of Discovery. The 17th century brought further enhancements to the rings' scales and engravings, improving precision in readings and adapting them for both field use and observatory work. (1546–1601) illustrated variant ring instruments in his 1598 publication Astronomiæ instauratæ mechanica, showcasing their integration into advanced setups at his observatory for systematic stellar observations. By the 18th century, however, astronomical rings declined in practical use, overtaken by superior instruments like the —for angular measurements—and marine chronometers—for —due to their greater accuracy and ease in maritime contexts; rings persisted mainly as educational tools.

Design principles

Geometric basis

Astronomical rings are grounded in the geometry of the , an imaginary sphere of arbitrary large radius centered on the , upon which the positions of celestial bodies are projected. The instrument employs three interconnected rings to model essential elements of this sphere: the meridian ring, representing the observer's local meridian as a passing through the north , , and ; the equatorial ring, depicting the as a inclined at 90° to the 's rotational axis; and the ring, a small circle parallel to the equator used to determine the of celestial objects from the equatorial plane. These rings capture the fundamental coordinate system of the heavens, enabling the projection of equatorial coordinates ( and ) relative to the local horizon. To adapt the instrument to the observer's φ, the equatorial ring is tilted relative to the meridian ring such that its plane aligns parallel to the true horizon when the meridian ring is vertical, with the angle of inclination equal to φ. This ensures the rings conform to the local celestial geometry, where the rises to an altitude of 90° - φ at upper . The core geometric relation governing observations is the formula for the altitude h of a celestial body with δ at H (the from the local meridian): sin⁡h=sin⁡ϕsin⁡δ+cos⁡ϕcos⁡δcos⁡H\sin h = \sin \phi \sin \delta + \cos \phi \cos \delta \cos H This equation arises from spherical trigonometry in the astronomical triangle formed by the north celestial pole, the zenith, and the celestial object; applying the spherical law of cosines to the sides (co-latitude 90° - φ, co-declination 90° - δ, and zenith distance 90° - h) and angle H at the pole yields the relation after trigonometric rearrangement. Alignment of the rings relies on establishing perpendicularity and orientation to the local frame. The meridian ring is positioned vertically using a plumb line, while initial north-south alignment employs a magnetic compass or solar shadow projection along the ring's edge; once set, sightings through pinholes or along the ring edges verify the 90° orthogonality between the meridian and equatorial rings, ensuring accurate representation of celestial great circles. For portable designs, the compact, foldable arrangement allows quick deployment in the field. Sources of error in the geometric framework include , which bends light rays and elevates apparent altitudes by up to 35 arcminutes near the horizon (decreasing with ), and manufacturing tolerances in ring graduations and pivots, which limit angular precision to approximately 1° in historical examples.

Construction materials and techniques

Astronomical rings were primarily constructed from durable metals such as and during ancient and periods, valued for their and resistance to wear in observational use. In Greek and Roman antiquity, as described by Pappus, these materials allowed for the creation of graduated rings that could withstand repeated adjustments and alignments. Later, during the , elite instruments often featured silver or gold plating over bases to enhance corrosion resistance and aesthetic appeal, as seen in 16th-century examples preserved in collections. Portable versions were typically solid or for compactness and durability. Fabrication techniques evolved from basic casting in molds for the primary ring structures, common since Ptolemaic times, to intricate hand-engraving of scales using dividers for precise degree markings. Hinges, often fashioned from pins or simple joints, allowed rings to adjust for different latitudes, with surfaces polished to minimize during rotations. In workshops, for large fixed instruments, additional steps like applying plates over wooden cores (e.g., laminated or ) ensured both accuracy and longevity, as detailed in Tycho Brahe's Astronomiae Instauratae Mechanica. Size variations accommodated diverse applications, with fixed observatory rings reaching diameters up to 2 meters for enhanced visibility and stability, exemplified by Brahe's equatorial armillaries. Portable models, by contrast, measured 10-20 cm in diameter when deployed, suitable for fieldwork or personal use, as in 15th-16th century traveler's rings. Quality was gauged by the precision of graduations, typically in 1° increments for basic models but refined to 0.5° or finer in advanced instruments through meticulous and balance testing for suspension.

Types

Fixed astronomical rings

Fixed astronomical rings are early stationary instruments, often ancient or medieval, consisting of rigidly mounted rings to represent celestial coordinates like the meridian or , typically installed in observatories, cathedrals, or public spaces for timekeeping and . Unlike the portable three-ring design of Gemma's rings, these precursors—such as Ptolemy's equinoctial armillary rings described in the (2nd century CE)—used large metal rings (e.g., ) aligned to for observing solstices and equinoxes without movable parts. Installation involved precise orientation to the local meridian and , often via gnomons or , enabling demonstrations of solar positions and basic angular measurements. Examples include medieval Islamic observatory rings at Maragha () and later European meridian circles in universities, though they differed from portable innovations by lacking foldability. Their stability allowed for larger scales but limited use to fixed locations, contrasting with mobile variants for .

Portable astronomical rings

Portable astronomical rings, designed for mobility, featured lightweight brass or similar metal frames that allowed for easy transport and adjustment in the field. These instruments often incorporated folding mechanisms or hinged components to collapse into a compact form suitable for pocket carry, with adjustable scales enabling use at various latitudes worldwide. Invented by Gemma Frisius in the early as a portable equatorial tool, they served astronomers, surveyors, and travelers by simplifying celestial observations without requiring fixed installations. Among the subtypes, the traveler's ring, also known as the universal equinoctial ring dial, included an additional hour ring for determining local time alongside latitude measurements, making it ideal for voyagers needing versatile timekeeping. This variant evolved from Frisius's design and became favored by sailors for its adaptability across global locations. The sun ring represented a simplified configuration focused primarily on measuring solar altitudes to compute latitude, reducing complexity for quick field assessments. Meanwhile, the sea ring, or nautical ring, invented by Pedro Nunes in the 16th century, was specifically adapted for maritime use to gauge the sun's height for latitude determination at sea, addressing the challenges of shipboard observations. Further adaptations enhanced their practicality for travel, such as protective cases to safeguard against damage during long voyages. These features underscored their role in , where durability and ease of use were paramount. Portable astronomical rings gained widespread popularity among 16th- and 17th-century navigators and surveyors, who relied on them for practical during expeditions and maritime voyages. Their compact design facilitated use in dynamic environments, from ocean crossings to land surveys, influencing tools carried by figures like European explorers.

Operation

Time and latitude measurement

Astronomical rings were employed to determine local by aligning the instrument with the sun and reading the on its graduated scales. The procedure begins by suspending the ring freely from a point on the meridian ring adjusted to the observer's known , ensuring the ring lies horizontal. The ring or is then rotated to match the sun's altitude, sighted through vanes or pinholes until the sun's ray passes through both apertures and casts a shadow or spot aligned with the scale. The is read from the equatorial scale, representing the sun's position relative to the local meridian; this angle is converted to local apparent time by dividing by 15° per hour, with further adjustment to mean using the equation of time correction for seasonal variations, as tabulated in ephemerides or standard astronomical tables (e.g., approximately +14 minutes in mid-February, -4 minutes in early ). To measure the observer's latitude, the instrument is set at solar noon, when the sun crosses the meridian. The meridian ring is positioned vertically in the north-south plane, often using a plumb line or bubble level for alignment, and the sun is sighted through the vanes to find its maximum altitude hh on the graduated arc. The latitude ϕ\phi is then calculated as ϕ=90∘−h+δ\phi = 90^\circ - h + \delta, where δ\delta is the sun's declination for that date, obtained from astronomical tables or ephemerides. This method relies on the geometric relationship in spherical astronomy, where the co-latitude complements the zenith distance adjusted for the sun's position relative to the celestial equator. Alignment steps for both measurements involve suspending the ring to allow free pivoting, leveling the base with a or integrated level, and orienting toward using a or known meridian reference before sighting the sun. Vane adjustments ensure precise ray passage, minimizing errors. Accuracy is highest at the equinoxes when δ=0∘\delta = 0^\circ, eliminating declination errors and simplifying to ϕ=90∘−h\phi = 90^\circ - h; otherwise, imprecise δ\delta values or misalignment can introduce errors up to 2° in determinations, while time readings may vary by several minutes due to sighting limitations and the sun's of about 0.5°.

Celestial declination determination

Astronomical rings facilitate the determination of by modeling key elements of the , allowing observers to sight celestial bodies and align the instrument's components to derive the north or south of the . The primary ring represents the , while the ring is graduated to indicate degrees of , and the meridian ring aligns with the observer's local meridian. To measure the sun's , the instrument is first adjusted for the observer's by sliding or pivoting the rings accordingly, ensuring the equator and meridian rings are oriented correctly relative to the horizon and . At solar noon, during the sun's meridian transit, the observer suspends or holds the ring steady with the meridian ring vertical and aligned north-south, then sights the sun through the alidade's pinholes or vanes on the declination ring. When the sun is properly sighted along the meridian plane, the position of the declination ring directly indicates the sun's declination on its graduated scale, as the instrument's translates the observed altitude into the equatorial coordinate without additional . This direct reading is possible because the rings are calibrated such that, at known latitude, the angular offset from the equatorial plane corresponds to when the body crosses the meridian. For observations away from the meridian, where AA (measured from the south) is involved, δ\delta is calculated using the formula: δ=arcsin⁡(sin⁡hsin⁡ϕ−cos⁡hcos⁡ϕcos⁡A)\delta = \arcsin\left( \sin h \sin \phi - \cos h \cos \phi \cos A \right) where hh is the observed altitude, ϕ\phi is the latitude, and AA is the azimuth. The altitude hh and azimuth AA are obtained by sighting the sun through the alidade and noting the ring alignments. For stars, the procedure mirrors that for the sun, with the rings adjusted to latitude and the celestial body sighted at or near meridian transit using the small apertures on the alidade. However, accurate measurement requires prior calibration against stars of known declination to verify alignment, as the instrument's scale must be zeroed against a reference. The limited size of the sighting vanes and apertures restricts precision for faint stars, often necessitating brighter, well-known objects like those in major constellations for reliable readings. As a calendar tool, the astronomical ring tracks the sun's varying declination over the year, enabling predictions of solstices (when δ≈±23.44∘\delta \approx \pm 23.44^\circ) and equinoxes (δ=0∘\delta = 0^\circ) by aligning the date scale on the declination ring and observing seasonal changes in solar position. This functionality supported agricultural planning in historical contexts, such as determining optimal planting times based on solar cycles. Key limitations include primary suitability for daytime solar observations, as the sun provides a bright target for sighting; nighttime stellar measurements demand a steady hand to maintain alignment through narrow apertures, reducing accuracy for dim objects. Additionally, the instrument's portability comes at the cost of precision compared to larger fixed observatories, with errors amplified by or misalignment.

Legacy

Notable historical examples

An early example of a meridian ring used in astronomy appears in the works of the 10th-century Persian scholar , who described a large meridian ring fixed in the plane of the meridian for observing solar transits and determining geographical coordinates. This instrument, set up at Jurjaniyya around 1016–1018, allowed to measure the meridian altitude of the sun with high precision, contributing to his calculations of Earth's radius and variations; though no physical artifact survives, its design influenced later Islamic observational tools. A prominent example of a portable astronomical ring is the 1575 brass ring dial crafted by English instrument maker Humfrey Cole, preserved in the British Museum and noted for its use in navigation during the Elizabethan era. This gilt copper-alloy device features adjustable bands with scales calibrated for latitudes between 50° and 56° north, including specific markings for London at 51°34', enabling sailors to compute time, declination, and position via solar observations; its inscriptions include Cole's signature and a perpetual calendar starting in 1575, showing signs of use-related wear such as patina and minor engravings. Another surviving 16th-century portable ring, a astronomical instrument dated and held in the in , exemplifies Flemish craftsmanship with custom latitude adjustments and zodiac engravings for traveler's use. Inscribed with the "Nepos Gemae F. Louany fecit," it includes dedicated scales for equatorial and polar observations, highlighting the rings' role in personal astronomy; the artifact is in good condition, with minimal corrosion, underscoring its historical portability for explorers. A finger-ring from 1555, also in the , represents a jeweled variant with inscribed biblical dedications and enamel zodiac scales tailored for approximate use in . Its outer hoop bears the Latin inscription "DIXIT ET FACTA SUNT IPSE MANDAVIT ET CREATA SUNT VERBO DEI CELI FIRMATI SUNT 1555," combining devotional elements with functional rings for celestial tracking; preserved in stable condition since its 1897 acquisition, it illustrates the blend of ornament and utility in artifacts.

Modern replicas and influence

In the 20th and 21st centuries, several makers have produced functional replicas of astronomical rings, often crafted from or to replicate 17th- and 18th-century designs. For instance, Briar and Bone offers a hanging astronomical ring dial cast in solid , measuring 45 mm in diameter, which serves as a portable for determining and basic astronomical measurements; priced at approximately $65 as of November 2025, it includes an instructional booklet for practical use. Similarly, Decorar con Arte's astronomical ring dial, made from zamac with a finish and mounted on a sapelli wood base, functions as a universal equatorial for latitude-aligned timekeeping and costs around 173 euros. These reproductions emphasize historical accuracy while making the instrument accessible for contemporary users. Such replicas play a significant role in STEM education and historical reenactments, allowing students and enthusiasts to engage hands-on with Renaissance-era astronomy. In educational settings, they demonstrate principles of celestial geometry, as seen in classroom projects where students construct simplified versions using tools like laser cutters to explore equinoctial time and solar positioning. Planetariums and museums, such as the Whipple Museum of the , incorporate related armillary instruments—direct precursors to ring dials—for interactive demonstrations of the three-dimensional , fostering understanding of astronomical coordinates without modern electronics. Digital adaptations have extended the instrument's reach since the , with apps simulating ring functions for virtual learning. The app, developed by the University of Hong Kong's Technology-Enriched Learning Initiative, recreates a Ptolemaic model for measuring sun and star movements, enabling users to manipulate virtual rings on mobile devices to track celestial paths. Post-2020 virtual models, including 3D-printable designs available on platforms like Yeggi, allow amateur astronomers to produce low-cost, customizable replicas at home, often integrating digital simulations for enhanced accuracy in educational outreach. These tools bridge historical methods with modern technology, promoting accessible astronomy education. Astronomical rings have influenced the development of later and tools, serving as conceptual precursors to instruments like the through their use of aligned rings for angular measurements in both astronomy and . In broader culture, the rings' interlocking design has inspired artistic representations, particularly in 19th-century and jewelry, where they symbolize cosmic harmony and intellectual pursuit, as reflected in Renaissance-inspired motifs in novels depicting scholarly voyages. Recent 3D-printed versions further this legacy, enabling amateur astronomers to experiment with functional models that echo the rings' role in early positional astronomy.

References

  1. https://cudl.lib.cam.ac.uk/view/PR-WHIPPLE-STORE-00054-00024-00004
  2. https://www.britishmuseum.org/collection/object/H_1888-1201-316
  3. https://www.mhs.ox.ac.uk/epact/catalogue.php?ENumber=51230
  4. https://cudl.lib.cam.ac.uk/view/PR-WHIPPLE-STORE-00054-00024-00002
  5. https://quod.lib.umich.edu/d/did/did2222.0003.241/--astronomical-or-universal-ring?rgn=main;view=fulltext
  6. https://www.academia.edu/38127388/Rings_Armillae_and_Other_Spherical_Instruments
  7. https://latin-dictionary.net/definition/3578/annulus-annuli
  8. https://www.ancient-origins.net/artifacts-ancient-technology/armillary-spheres-following-celestial-objects-ancient-world-004025
  9. https://adsabs.harvard.edu/full/1999JHA....30..237E
  10. https://www.cambridge.org/core/books/new-history-of-greek-mathematics/mathematics-of-the-stars/545604551D218591AA5F8E5A40649D36
  11. https://penelope.uchicago.edu/Thayer/E/Roman/Texts/Vitruvius/9*.html
  12. https://www.gutenberg.org/files/20239/20239-h/20239-h.htm
  13. https://inference-review.com/article/the-first-golden-age-of-islamic-science
  14. https://www.tandfonline.com/doi/full/10.1080/00033790310001642795
  15. https://mathshistory.st-andrews.ac.uk/Biographies/Gemma_Frisius/
  16. https://www.mhs.ox.ac.uk/exhibits/the-renaissance-in-astronomy/objects/22-astro-rings-arsenius-1567/index.html
  17. https://library.si.edu/digital-library/book/tychonisbraheas00braha
  18. https://www.thecollector.com/astrolabes-sextants-ancient-mariners-navigation/
  19. https://institutions.ville-geneve.ch/fileadmin/user_upload/mhn/images/votre_visite/site_mhs/5_Univers_2024.pdf
  20. https://www.mhs.ox.ac.uk/students/98to99/Inst/Instpgs/2a.Gemmasrings.html
  21. https://pages.astronomy.ua.edu/keel/techniques/astrom.html
  22. https://adsabs.harvard.edu/full/2006Obs...126...82Y
  23. https://www.peterbeard.net/tycho-brahe-at-hven.html
  24. https://www.si.edu/object/equatorial-armillary-sphere%253Anmah_1187570
  25. https://giftsforadesigner.com/products/16th-century-german-astronomical-ring-a-token-of-love
  26. https://academic.oup.com/book/9389/chapter/156217734
  27. http://www.sites.hps.cam.ac.uk/starry/armillobser.html
  28. https://mathshistory.st-andrews.ac.uk/Strick/gemma_frisius.pdf
  29. https://www.rmg.co.uk/collections/objects/rmgc-object-10472
  30. https://collections.sea.museum/en/objects/165681/universal-equinoctial-ringdial
  31. http://cvc.instituto-camoes.pt/ciencia_eng/e29.html
  32. https://artsandculture.google.com/story/nautical-instruments-museu-de-marinha/GwVRXn4Z0ONstg?hl=en
  33. https://nwcartographic.com/blogs/essays-articles/regnier-gemma-frisius-1508-1555
  34. https://pubs.nmsu.edu/_circulars/CR674/index.html
  35. https://link.springer.com/article/10.1007/s00407-023-00312-2
  36. https://www.survivorlibrary.com/library/a_history_of_nautical_astronomy_1968.pdf
  37. https://www.persoaryanstudies.org/uploads/1/4/3/4/143405260/gnomon.pdf
  38. https://www.encyclopedia.com/people/science-and-technology/astronomy-biographies/abu-rayhan-al-biruni
  39. https://www.britishmuseum.org/collection/object/H_1905-0608-1
  40. https://www.mhs.ox.ac.uk/epact/catalogue.php?ENumber=89914
  41. https://collection.sciencemuseumgroup.org.uk/objects/co1278/astronomical-ring
  42. https://www.britishmuseum.org/collection/object/H_AF-1759
  43. https://www.briarandbone.com/hanging-astronomical-ring-dial.html
  44. https://www.decorarconarte.com/en/p/anillo-astronomico-10x04cm/
  45. https://community.glowforge.com/t/freshman-geometry-project-astronomical-rings/19880
  46. https://www.whipplemuseum.cam.ac.uk/explore-whipple-collections/astronomy/armillary-spheres-and-teaching-astronomy
  47. https://teli.hku.hk/armillary-sphere/
  48. https://www.yeggi.com/q/astronomical%2Bring/
  49. https://thonyc.wordpress.com/2023/01/13/renaissance-science-xlviii/
  50. https://www.thisiscolossal.com/2025/10/gold-armillary-rings-astronomy-history-jewelry/
Add your contribution
Related Hubs
User Avatar
No comments yet.