Cubic surface

Cubic surfaceMain

Community hub

Cubic surface

8 pages, 0 posts

0 subscribers

Recent from talks

Be the first to start a discussion here.

Recent from talks

Be the first to start a discussion here.

Contribute something

About hubMembersContent overviewUpdatesRules

Main reference articles

Cubic surface

View on Wikipedia

from Wikipedia

Not found

Revisions and contributors Edit on Wikipedia Read on Wikipedia

View on Grokipedia

from Grokipedia

A cubic surface is a smooth projective hypersurface of degree three in three-dimensional projective space

\mathbb{P}^3

, defined over an algebraically closed field (typically the complex numbers) by a homogeneous polynomial equation

F(x,y,z,w) = 0

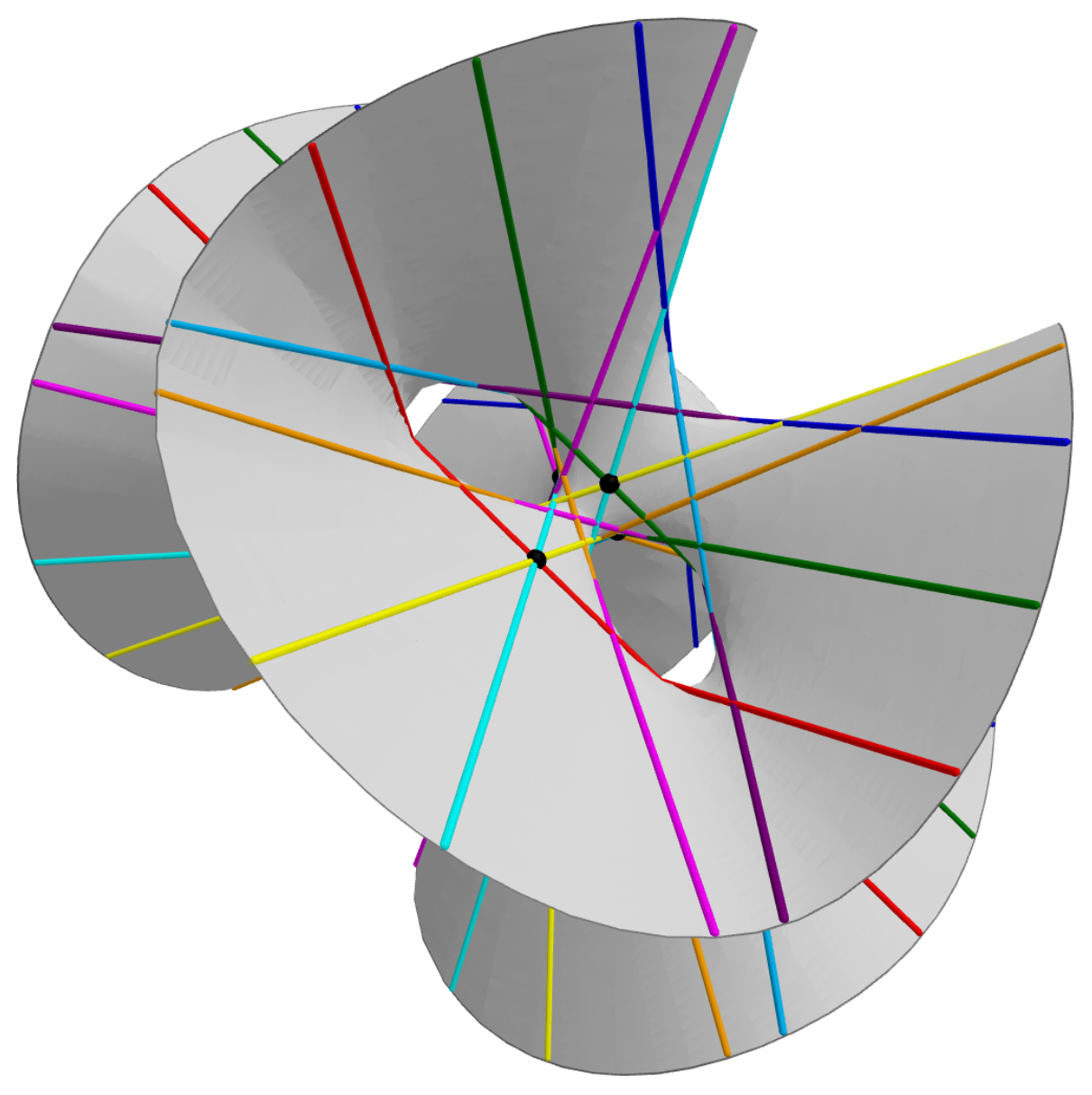
of degree three.^[1] These surfaces are fundamental objects in algebraic geometry, serving as the simplest nontrivial examples of algebraic surfaces beyond quadrics and planes.^[1] One of the most striking features of a smooth cubic surface is that it contains exactly 27 lines, a classical result first proved by Arthur Cayley and George Salmon in 1849, who showed that this is the maximum finite number of straight lines lying on such a surface.^[2] These lines are exceptional curves with self-intersection number

-1

, and their configuration—where each line intersects exactly ten others—generates the Picard group of the surface, which has rank seven and is isomorphic to the lattice

I^{1,6}

.^[1] The lines can be classified into types based on their normal bundles, with those of the second type lying in a unique tangent plane.^[1] Cubic surfaces are rational varieties, meaning they are birational to the projective plane

\mathbb{P}^2

via the blow-up at six general points, which resolves the indeterminacies of the rational map given by the linear system of cubics through those points.^[1] This birational equivalence highlights their role in enumerative geometry and moduli theory, where the four-dimensional moduli space of cubic surfaces exhibits rich period maps and monodromy actions related to the Weyl group

W(E_6)

.^[1] Historically, the study of cubic surfaces advanced 19th-century algebraic geometry, with contributions from Ludwig Schläfli on singular cases and later developments linking them to derived categories and hyperkähler geometry in higher-dimensional analogs like cubic fourfolds.^[2]

Fundamentals

Definition and General Form

A cubic surface is defined as a hypersurface of degree 3 in the projective 3-space

\mathbb{P}^3

over an algebraically closed field, typically

\mathbb{C}

.^[1] It is the zero locus of a homogeneous polynomial equation of degree 3 in the four homogeneous coordinates of

\mathbb{P}^3

.^[1] The general form of such a surface is given by

F(x, y, z, w) = 0,

where

F

is a cubic homogeneous polynomial in the variables

x, y, z, w

.^[1] A standard example is the Fermat cubic surface, normalized as

x^3 + y^3 + z^3 + w^3 = 0,

which is smooth provided the characteristic of the base field is not 3.^[1] For intuition in affine coordinates, one considers affine charts via dehomogenization; for instance, setting

w = 1

yields an affine cubic surface in

\mathbb{A}^3

defined by the corresponding inhomogeneous equation.^[3] The parameter space of all cubic surfaces in

\mathbb{P}^3

is the projective space

\mathbb{P}^{19}

, corresponding to the 20 monomials of degree 3 in four variables, up to scalar multiple.^[1] Accounting for the action of the projective linear group

\mathrm{PGL}(4)

, which has dimension 15, the moduli space of smooth cubic surfaces is 4-dimensional.^[4]

Smoothness and Projective Embedding

A cubic surface in projective 3-space

\mathbb{P}^3

, defined by a homogeneous cubic polynomial

F(x, y, z, w) = 0

, is smooth if it contains no singular points. A point

[x : y : z : w] \in \mathbb{P}^3

is singular if

F = 0

and all partial derivatives

\partial F / \partial x_i = 0

for

i = 0, 1, 2, 3

, where the variables are indexed accordingly.^[5] This condition follows from the Jacobian criterion for hypersurfaces, which states that a hypersurface variety is smooth at a point if the rank of the Jacobian matrix (here, the row of partial derivatives) is equal to the codimension, ensuring the tangent space dimension matches the expected value.^[6] For cubic surfaces, singularities occur only if the gradient

\nabla F

vanishes simultaneously with

F

at some point, and over algebraically closed fields, smooth cubics are non-singular by generic choice of coefficients.^[1] Smooth cubic surfaces embed naturally as degree-3 subvarieties of

\mathbb{P}^3

via the complete linear system associated to the anticanonical bundle

|-K_X|

, where

K_X

denotes the canonical divisor. By the adjunction formula for hypersurfaces,

K_X = (K_{\mathbb{P}^3} + X)|_X = (-4H + 3H)|_X = -H|_X

, with

H

the hyperplane class pulled back from

\mathcal{O}_{\mathbb{P}^3}(1)

.^[7] This embedding realizes the surface as a del Pezzo surface of degree 3, since the degree is

K_X^2 = (-H)^2 = H^2 = 3

, confirming that

-K_X

is very ample. Over the complex numbers, the Picard group

\mathrm{Pic}(X)

has rank 7 and is generated by the hyperplane class

H

together with the classes of the 27 lines on the surface, isomorphic to the lattice

I^{1,6}

. Over number fields, the generic smooth cubic surface has Picard rank

\rho(X) = 1

, with

\mathrm{Pic}(X)

generated by

H

.^[1] A hyperplane section of a smooth cubic surface is a smooth plane cubic curve, whose genus is given by the formula for irreducible plane curves of degree

d

g = (d-1)(d-2)/2

. For

d=3

, this yields

g=1

, so the section is an elliptic curve.^[8] This elliptic nature highlights the surface's role in connecting cubic geometry to abelian varieties.

Geometric Features

The 27 Lines

A fundamental feature of smooth cubic surfaces is the presence of exactly 27 lines. Over an algebraically closed field of characteristic not equal to 2 or 3, every smooth cubic surface in projective 3-space contains precisely 27 lines, a result originally established by Arthur Cayley and George Salmon in 1849.^[2]^[9] To see this via intersection theory, note that any line on the surface is a smooth rational curve of degree 1 with respect to the hyperplane class

H

. By the adjunction formula, for such a curve

C

, we have

2g-2 = C^2 + C \cdot K_S

, where

g=0

is the genus and

K_S

is the canonical class. Since

K_S = -H

on the cubic surface, this simplifies to

-2 = C^2 - C \cdot H = C^2 - 1

, yielding

C^2 = -1

. Thus, lines correspond to effective curves in the anticanonical class

-K_S = H

with self-intersection

-1

. The space of such curves is finite, and enumerative methods, such as Schubert calculus on the Grassmannian

\mathrm{Gr}(2,4)

, show there are exactly 27 of them.^[10]^[11] The 27 lines exhibit a rich combinatorial structure known as the Cayley-Salmon configuration, which realizes the root lattice of the exceptional Lie algebra

E_6

. In this setup, the intersection form on the Picard group orthogonal to

K_S

is isometric to the

E_6

lattice, with the classes of the lines corresponding to a set of 27 vectors of norm

-1

. Each line intersects exactly 10 others transversely at distinct points, as determined by the inner products in the lattice: the total number of intersecting pairs is

\frac{27 \times 10}{2} = 135

, while the remaining

\binom{27}{2} - 135 = 216

pairs are skew. This incidence graph encodes triples of mutually skew lines or concurrent lines in specific ways, reflecting the

E_6

symmetry.^[1]^[12] A special incidence occurs at Eckardt points, where three lines meet concurrently. These points are exceptional features, with most smooth cubic surfaces having none, though up to 18 are possible, as realized on the Fermat cubic surface

x^3 + y^3 + z^3 + w^3 = 0

. The presence of Eckardt points corresponds to a codimension-1 subset in the moduli space of cubic surfaces and influences the surface's automorphism group.^[13]^[14]

Blow-up Realization

A smooth cubic surface over an algebraically closed field is birationally equivalent to the blow-up of the projective plane

\mathbb{P}^2

at six points in general position, meaning no three points are collinear and the six points do not lie on a conic.^[15] This construction yields a del Pezzo surface of degree 3, where the exceptional divisors

E_1, \dots, E_6

arise from the blown-up points.^[15] Let

\pi: X \to \mathbb{P}^2

denote the blow-up morphism, with pullback of the hyperplane class

H

\mathbb{P}^2

. The anticanonical divisor on

X

-K_X = 3H - \sum_{i=1}^6 E_i

, which is very ample and embeds

X

into

\mathbb{P}^3

via the complete linear system

|-K_X|

, realizing

X

as a cubic surface in

\mathbb{P}^3

.^[15] The self-intersection

(-K_X)^2 = 3

confirms the degree of the embedded surface, computed as follows:

(-K_X)^2 = (3H - \sum E_i)^2 = 9H^2 - 6 \sum (H \cdot E_i) + \sum E_i^2 + 2 \sum_{i < j} (E_i \cdot E_j) = 9 - 6 = 3,

using

H^2 = 1

H \cdot E_i = 0

E_i^2 = -1

, and

E_i \cdot E_j = 0

for

i \neq j

.^[15] The exceptional divisors

E_i

correspond to six of the 27 lines on the cubic surface. The remaining lines are the proper transforms of lines through pairs of points, given by classes

H - E_i - E_j

for

i \neq j

(15 lines), and the proper transforms of conics through five points, given by

2H - \sum_{k \neq i} E_k

(6 lines).^[15] Over an algebraically closed field, every smooth cubic surface is isomorphic to such a blow-up at six general points.^[15] The birational map from

X

to the cubic is given by the projection from the linear system

|-K_X|

, parametrizing the embedding.^[15]

Algebraic Properties

Rationality

A smooth cubic surface over an algebraically closed field of characteristic zero is unirational, as the projection from any line on the surface induces a dominant rational map to

\mathbb{P}^2

.^[1] This follows from the existence of 27 lines on such a surface and the general fact that a smooth cubic hypersurface containing a line is unirational via projection.^[16] Full rationality holds, as every smooth cubic surface is birational to

\mathbb{P}^2

. This birational equivalence arises as the inverse of the blow-up of

\mathbb{P}^2

at six points in general position—no three collinear and no six on a conic—established by Clebsch in 1871.^[1] An explicit birational map can be constructed via stereographic projection from a point on the surface not lying on any of the 27 lines, parametrizing the surface rationally in terms of two parameters.^[16] For the Clebsch diagonal cubic, defined as the intersection of the hypersurface

x_0^3 + x_1^3 + x_2^3 + x_3^3 + x_4^3 = 0

\mathbb{P}^4

with the hyperplane

x_0 + x_1 + x_2 + x_3 + x_4 = 0

, embedding it in

\mathbb{P}^3

, an explicit rational parametrization exists using quadratic forms in two variables, reflecting its symmetry under the action of

S_5

.^[17] This parametrization highlights the surface's rationality and its 27 real lines.^[18] The rationality of smooth cubic surfaces over algebraically closed fields was classically established through the blow-up model by Clebsch and Noether in the late 19th century, with arithmetic aspects for non-closed fields developed by Coray and Tsfasman in 1983, building on Noether's methods for birational classification.^[19]^[20]

Automorphisms of Smooth Cubics

The automorphism group

\operatorname{Aut}(X)

of a smooth cubic surface

X \subset \mathbb{P}^3_k

over an algebraically closed field

k

of characteristic zero is finite and isomorphic to a finite subgroup of

\operatorname{PGL}(4,k)

.^[21] This group consists of projective linear transformations that preserve the defining equation of

X

. For a general smooth cubic surface,

\operatorname{Aut}(X)

is trivial, reflecting the discrete nature of the moduli space at generic points, which has dimension 4.^[21] The group

\operatorname{Aut}(X)

acts on the Picard group

\operatorname{Pic}(X) \cong \mathbb{Z}^7

, preserving the hyperbolic intersection form of signature (1,6) on

H^2(X,\mathbb{Z})

.^[21] This action is faithful, embedding

\operatorname{Aut}(X)

into the orthogonal group

O(\operatorname{Pic}(X))

, which is generated by reflections across the classes of the 27 exceptional lines and isomorphic to the Weyl group

W(E_6)

of order 51840.^[21] The isomorphism

W(E_6) \cong O^+(6,2)

highlights the exceptional Lie structure underlying the geometry.^[21] Thus, every automorphism induces a permutation of the 27 lines on

X

, with the image lying in a conjugacy class of subgroups of

W(E_6)

. Computations of

\operatorname{Aut}(X)

rely on classifying these induced actions on the Picard lattice, often via normal forms of the defining equation or counts of invariant lines and Eckardt points.^[21] All possible finite groups arising this way over characteristic zero have been classified, with orders ranging from 1 up to 648.^[21] Exceptional cases feature larger automorphism groups. The Fermat cubic surface, defined by

x_0^3 + x_1^3 + x_2^3 + x_3^3 = 0

, has

\operatorname{Aut}(X) \cong (\mathbb{Z}/3\mathbb{Z})^3 \rtimes S_4

of order 648, generated by scalar multiplications of order 3 on coordinates and permutations thereof.^[21] The Clebsch cubic surface, defined by

\sigma_1 \sigma_2 - \sigma_3 = 0

where

\sigma_i

are elementary symmetric polynomials in the coordinates, has

\operatorname{Aut}(X) \cong S_5

of order 120, arising from its 10 Eckardt points and icosahedral symmetry.^[21] These groups represent the maximal and notable exceptional symmetries, with loci of codimension 4 in the moduli space.^[21]

Singular Cases

Classification of Singularities

Singular cubic surfaces in

\mathbb{P}^3

over an algebraically closed field of characteristic zero possess isolated singularities that are rational double points, known as du Val singularities, which are classified by the ADE Dynkin diagrams up to type E

_6

. These singularities arise as hypersurface singularities defined by a cubic equation locally near the singular point, and their type is determined by the multiplicity and the structure of the tangent cone. The minimal resolution of such a singularity is achieved by blowing up the singular point successively, yielding an exceptional locus consisting of a chain or tree of

(-2)

-curves whose dual graph is the corresponding Dynkin diagram. The full classification of singular cubic surfaces by their singularities comprises 22 distinct types, encompassing combinations of multiple singularities of various ADE types, as established by Bruce and Wall. These types include single singularities like A

_1

, A

_2

, ..., A

_5

, D

_4

, D

_5

, E

_6

, and

\widetilde{E}_6

6, as well as multiple ones such as 2A $_1$ , 3A $_1$ , 4A $_1$ , A $_1$ A $_2$ , up to configurations like 3A $_2$ . Ordinary singularities are those with a non-degenerate quadratic tangent cone, primarily nodes of type A $_1$ (local equation $xy + z^2 +$ higher terms $= 0$ ) and cusps of type A $_2$ (local equation $x^2 + y^3 +$ higher terms $= 0$ ), extending to higher A $_n$ and D/E types where the blow-up process aligns with the hypersurface structure. A cubic surface admits at most four nodes, with equality realized uniquely by Cayley's nodal cubic surface. Non-ordinary singularities, such as A $_5$ , D $_5$ , and the parabolic $\widetilde{E}_6$

6, feature a degenerate tangent cone and lie on the Hessian discriminant surface, complicating their local analytic structure beyond simple quasi-homogeneity. Cusp singularities of higher order (A $_n$ for $n \geq 2$ ) and their resolutions involve extended blow-up sequences, where the exceptional curves form a linear chain of length $n$ , but non-ordinary cases may require additional normalization steps. The dimension of the parameter space for cubics with a prescribed singularity type varies; for example, the locus of cubics with four A $_1$ singularities is 0-dimensional (a single orbit under PGL(4)), while those with a single E $_6$ form a curve.^[22] Modern computational algebraic geometry has refined this classification by linking singularity types to invariants like the rank of the apolar ideal and exploring degenerations. Seigal computed the possible ranks (from 3 to 6 for isolated singularities) for each of the 22 types, showing that non-ordinary singularities correspond to rank-6 forms whose zero loci close the Hessian discriminant. Additionally, toric degenerations of smooth cubic surfaces, obtained by degenerating their Cox rings to toric algebras via Khovanskii bases, yield singular toric fibers whose singularities are toric rational double points, classifiable combinatorially by the associated cones; computational enumeration identifies 78 moneric classes, with 38 being Khovanskii bases supporting quasi-smooth toric models where singularities occur only at torus-fixed points. These approaches, using tools like Macaulay2 and tropical geometry, extend the classical list to families of semi-stable reductions over discrete valuation rings.^[22]^[23]

Lines on Singular Cubics

Singular cubic surfaces, classified by their rational double point singularities of ADE type, exhibit a reduced number of lines compared to the 27 on smooth cubics, with the count varying by singularity configuration. For instance, a surface with a single nodal singularity of type

A_1

contains exactly 21 lines, reflecting the coalescence of six lines from the smooth case into pairs intersecting at the node.^[24] More generally, across ADE types, the numbers decrease as follows: 21 for

A_1

, 15 for

A_2

, and 1 for

E_6

, as detailed in recent analyses of line configurations on resolved models.^[24] Lines on these singular surfaces often persist through the singularities or become tangent to the singular locus, altering their intersections from the skew configurations typical in smooth cases. Computationally, such lines can be identified by restricting the defining cubic equation to parametrized lines and imposing identical vanishing, with special attention to those passing through singular points where partial derivatives vanish; these must lie within the projectivized tangent cone while satisfying higher-order conditions from the cubic terms. In singular settings, configurations change such that multiple lines may coincide at the singularity or embed within the exceptional strata of the minimal resolution, reducing the total distinct count and modifying incidence relations. A prominent example is the Cayley cubic surface, defined by the equation

\sum_{i<j<k} x_i x_j x_k = 0

(up to projective equivalence), which possesses four

A_1

nodal singularities and exactly 9 lines: six forming the edges of a tetrahedron through the nodes and three additional transversal lines.^[25] Another illustrative case arises in projections related to higher-degree surfaces like the Barth sextic, where the cubic model inherits a singular structure with 9 lines concentrated near the projected singularities, emphasizing the persistence of linear features despite degeneracy. Recent work, including updates from Manin's perspectives on cubic geometry in the 2020s, confirms these counts for all ADE configurations, linking them to the root lattices underlying the singularities.

Automorphism Groups of Singular Cubics

Singular cubic surfaces in projective 3-space often admit larger automorphism groups compared to their smooth counterparts, owing to the additional flexibility introduced by singularities, which can act as fixed points or orbits under group actions. The classification of these groups is particularly tractable for "parameter-free" cases, where the normal forms of the surfaces have no free parameters, leading to rigid geometries without moduli spaces. In these instances, the automorphism groups can be finite or infinite, depending on the singularity type, and are determined by the action on the resolved surface and its exceptional divisors. A comprehensive classification of automorphism groups for normal singular cubic surfaces with no parameters, based on their ADE or elliptic singularities, reveals a variety of structures. For surfaces with rational double points (ADE types), the groups range from small finite ones like

\mathbb{Z}/2\mathbb{Z}

for a single node (

A_1

) to larger finite groups such as the symmetric group

S_4

for the four-nodal case (

4A_1

). Other examples include semi-direct products involving multiplicative groups for more complex configurations, such as

(\mathbb{C}^\times)^2 \rtimes S_3

for three

A_2

singularities. These groups preserve the singularity configuration and act faithfully on the resolved minimal model. The following table summarizes key parameter-free cases and their automorphism groups:

Singularity Type	Automorphism Group	Notes
$A_1$	$\mathbb{Z}/2\mathbb{Z}$	Single node; involution swapping exceptional curve.
$4A_1$	$S_4$	Four nodes; permutes the nodes transitively.
$3A_2$	$(\mathbb{C}^\times)^2 \rtimes S_3$	Infinite; acts on three cusps.
$A_5$	$(\mathbb{C} \rtimes \mathbb{Z}/3\mathbb{Z}) \rtimes \mathbb{Z}/2\mathbb{Z}$	Finite extension involving rotations.

This classification highlights how singularities enhance symmetry, with finite groups arising in highly symmetric nodal configurations and infinite groups in those with elliptic or higher-codimension features. Automorphism groups are computed by resolving the singularities via successive blow-ups, typically at six points corresponding to the exceptional configuration, and analyzing the induced action on the Picard lattice of the minimal resolution, which is a hyperbolic lattice of rank 7 minus the singularity contributions. Monodromy representations from the deformation space of the resolved surface map to the orthogonal group of the lattice, revealing the finite part of the automorphism group, while the connected component arises from the identity component of the automorphism group of the anticanonical model. This approach leverages the fact that automorphisms lift uniquely to the resolution for normal surfaces. A prominent example is the Cayley cubic surface, defined by the equation

\sum_{i<j<k} x_i x_j x_k = 0

\mathbb{P}^3

, which has four nodes at the points

[1:\omega:\omega^2:0]

(and permutations), where

\omega

is a primitive cube root of unity. Its automorphism group is isomorphic to

S_4

of order 24, generated by permutations of the coordinate variables that preserve the symmetric form and transitively act on the nodes; lines on the surface serve as invariants under this action. Singular variants of the Fermat cubic, such as those with imposed nodes via parameter specialization, can yield groups like

\mathbb{Z}/2\mathbb{Z} \times S_3

for mixed nodal-cuspidal types, though these often introduce parameters.^[26] Recent studies have explored Cremona transformations that preserve singularity types on cubic surfaces, extending the classical automorphism groups. For instance, birational maps induced by quadratic transformations centered at singular points can generate additional finite subgroups isomorphic to Weyl groups like

W(E_6)

in resolutions of nodal cubics with Picard lattice

E_6

, acting as monodromy-invariant symmetries without altering the singularity locus. These transformations, analyzed post-2015, reveal hidden finite extensions in parameter-free families, such as order-51840 actions on certain three-nodal surfaces.^[27]

Variations over Fields

Real Cubic Surfaces

A smooth real cubic surface, embedded in real projective 3-space

\mathbb{RP}^3

, consists of the real points of a homogeneous cubic polynomial equation, forming a compact semi-algebraic set that is diffeomorphic to a smooth compact 2-manifold when the surface is nonsingular.^[28] The topology of this real locus varies depending on the specific equation, but classical results classify smooth cases into five diffeomorphism types based on the number of real lines and Euler characteristic: type I (27 real lines, connected non-orientable with

\chi = -5

), type II (15 real lines, connected non-orientable with

\chi = -3

), type III (7 real lines, connected non-orientable with

\chi = -1

), type IV (3 real lines, connected diffeomorphic to

\mathbb{RP}^2

with

\chi = 1

), and type V (3 real lines, disconnected

\mathbb{RP}^2 \sqcup S^2

with

\chi = 3

).^[28] These types arise from the blow-up construction of the cubic surface as

\mathbb{RP}^2

blown up at six points, where the reality of the points influences the connectedness and orientability of the real locus.^[28] The number of real lines on a smooth real cubic surface is constrained by Schläfli's classification into five types, with possible counts of 27, 15, 7, 3, or 3 real lines among the 27 complex lines (the latter two differing in the configuration of tritangent planes).^[29] The types with 27, 15, or 7 real lines are connected non-orientable, while those with 3 real lines can be either connected (

\mathbb{RP}^2

) or disconnected (

\mathbb{RP}^2 \sqcup S^2

).^[28] Harnack-type bounds limit the topological complexity; for instance, the real locus has at most two connected components in the smooth case, though the primary types have one or two. Oval arrangements on the real locus, arising from intersections with real hyperplanes (yielding real plane cubics with up to two components by Harnack's curve theorem), further distinguish configurations: in the maximal case of 27 real lines, the connected locus features arrangements of ovals and pseudolines bounded by the lines.^[28] The Clebsch diagonal cubic, given by the equation

81(x^3 + y^3 + z^3 + w^3) - 189(x^2 y + x^2 z + \cdots) + \cdots = 0

(in symmetric form), exemplifies the maximal configuration with all 27 lines real, lying on the connected non-orientable locus with Euler characteristic -5.^[30] Visualizations of real cubic surfaces often employ implicit plots in affine charts or stereographic projections from

\mathbb{RP}^3

\mathbb{R}^3

, revealing the lines as straight edges and ovals as closed curves; for the Clebsch surface, such projections highlight the icosahedral symmetry and the complete set of real lines forming a polyhedral skeleton.^[30] Recent computational studies using homotopy continuation methods have explored the distribution of real lines on random real cubic surfaces under the Kostlan measure, confirming Schläfli's counts while quantifying rarity: approximately 57% have 3 lines, 34% have 7, 8.9% have 15, and 0.14% have 27, with an expected average of about 5.46 real lines.^[31] These results, obtained via numerical path-tracking in parameter space, provide probabilistic insights into maximal configurations and enhance understanding of topological transitions between types.^[31] For singular real cubic surfaces, the presence of singularities (such as nodes or cusps) alters the topology of the real locus, introducing handles or modifying the Euler characteristic; for example, an

A_1

singularity (node) can yield a real locus diffeomorphic to a sphere with one handle (torus,

\chi=0

), while more severe singularities like

E_6

produce surfaces with multiple handles and reduced connectivity.^[32] The Euler characteristic of the real locus in singular cases often follows patterns like

\chi = 9 - 3k/2

adjusted for the number of real lines

l

and singularity contributions, though exact relations depend on the singularity type and real line count.^[32]

Cubic Surfaces over Arbitrary Fields

Cubic surfaces over a non-algebraically closed field

k

are smooth projective varieties defined by the vanishing of a homogeneous cubic polynomial in

\mathbb{P}^3_k

. Unlike over algebraically closed fields, where all smooth cubic surfaces are rational and contain exactly 27 lines, the arithmetic of the base field introduces obstructions to the existence of

k

-points, lines, and rationality. Over perfect fields, a smooth cubic surface is

k

-rational if and only if it admits a

k

-point, as the presence of such a point implies unirationality, and unirationality for surfaces over perfect fields yields rationality by Castelnuovo's theorem.^[33]^[34] Descent theory provides a framework for classifying cubic surfaces up to

k

-isomorphism using Galois cohomology. A cubic surface

S

defined over

k

can be viewed as a twist of a model over the algebraic closure

\overline{k}

, and the possible descent data correspond to elements in the cohomology group

H^1(k, \mathrm{PGL}(4))

, reflecting the action of the absolute Galois group

\mathrm{Gal}(\overline{k}/k)

on the space of cubic forms under the projective linear group. This cohomology group parametrizes the isomorphism classes of cubic surfaces embedded in

\mathbb{P}^3_k

, allowing for the study of minimal models and the arithmetic invariants preserved under Galois action. For del Pezzo surfaces of degree 3, such descent data also governs the Galois orbits on the 27 lines over

\overline{k}

, determining the number of

k

-lines.^[1] The Brauer-Manin obstruction plays a central role in explaining failures of the Hasse principle for the existence of

k

-points on smooth cubic surfaces over number fields, such as

\mathbb{Q}

. Defined via the pairing between the product of local points and the algebraic Brauer group

\mathrm{Br}(S)/\mathrm{Br}(k)

, this obstruction detects non-trivial classes in the Brauer group that prevent global points despite local solubility everywhere. The first explicit example of a smooth cubic surface over

\mathbb{Q}

violating the Hasse principle was constructed by Swinnerton-Dyer in 1962, given by the equation

5x^3 + 9y^3 + 10z^3 + 12w^3 = 0

; this surface has points over every completion of

\mathbb{Q}

but none over

\mathbb{Q}

, and the failure is explained by a non-trivial Brauer-Manin obstruction arising from a cyclic algebra of order 3. Subsequent examples, including infinite families of diagonal cubic surfaces, confirm that the obstruction accounts for most known counterexamples to the Hasse principle in this setting.^[35]^[36] Failures of weak approximation also occur for cubic surfaces over number fields, even when

k

-points exist. Weak approximation requires that the set of

k

-points is dense in the product of local points with respect to the adelic topology, but the Brauer-Manin obstruction can prevent this by imposing conditions on the local invariants of Brauer classes. For instance, on certain smooth cubic surfaces over

\mathbb{Q}

with rational points, the obstruction leads to a positive-dimensional image in the Sha group, violating weak approximation at finitely many places while allowing points elsewhere. These failures highlight the arithmetic complexity beyond mere existence of points.^[37] Over finite fields

\mathbb{F}_q

, the geometry of cubic surfaces is quantified through point counting, informed by the Weil conjectures. The number of

\mathbb{F}_q

-points on a smooth cubic surface

S

is given by

|S(\mathbb{F}_q)| = q^2 + q + 1 + \sum_{i=1}^{6} a_i

, where the

a_i

arise from the action of Frobenius on the primitive part of

H^2

(dimension 6), satisfying

|a_i| \leq 2 q

by Deligne's theorem (full trace bounded by 7q including the hyperplane class). The associated zeta function is

Z(S, T) = \frac{P_2(T)}{(1 - T)(1 - q T)(1 - q^2 T)}

, with

P_2(T)

a polynomial of degree 7 reflecting the second Betti number. Explicit computations for small

q

show that most smooth cubic surfaces over

\mathbb{F}_q

contain

\mathbb{F}_q

-lines, and the average number of points aligns with these bounds.^[38] The number of lines on a smooth cubic surface over any field

k

is uniformly bounded, taking values in the finite set {0, 1, 2, 3, 5, 7, 9, 15, 27}, as classified by Segre in 1949 using the incidence correspondence and properties of the Weyl group

W(E_6)

. Over number fields, recent work has explored the distribution and maximal possible numbers of

k

-lines; for example, no smooth cubic surface over

\mathbb{Q}

admits all 27 lines defined over

\mathbb{Q}

, with the maximum being 21 in known cases, though uniform bounds independent of the degree of the field remain open. Recent advances have refined estimates for the average number of lines over function fields analogous to number fields, supporting conjectures on boundedness under height constraints.^[39]^[40]

Advanced Structures

Moduli Space

The moduli space of smooth cubic surfaces over the complex numbers parametrizes isomorphism classes of such surfaces and is a 4-dimensional quasiprojective variety. The parameter space of all cubic surfaces in

\mathbb{P}^3

is the projective space

\mathbb{P}^{19}

of homogeneous cubic polynomials in four variables, which has dimension 19 since there are 20 monomials up to scalar multiple. The group

\mathrm{PGL}(4)

acts on this space with dimension 15, and since the stabilizer of a general smooth cubic surface is finite, the dimension of the moduli space is

19 - 15 = 4

.^[41] This moduli space can be constructed as a geometric invariant theory (GIT) quotient

\mathbb{P}^{19} // \mathrm{SL}(4)

, which is the Proj of the invariant ring generated by the classical invariants of cubic forms in four variables under the

\mathrm{SL}(4)

-action. The GIT quotient includes singular strata corresponding to cubic surfaces with worse singularities, such as nodes or cusps, stratified by the type of singularity; the smooth locus is open and dense in this 4-dimensional space. The construction dates back to classical work in 19th-century invariant theory, providing a classical description of the moduli.^[42]^[43] For marked cubic surfaces, where the 27 lines are labeled, the moduli space admits a period map to a bounded symmetric domain of type IV in

\mathbb{C}^4

, which uniformizes the unmarked moduli space as a quotient by a suitable arithmetic group acting discretely. This domain arises from the period domain for the orthogonal group associated to the lattice of the surface's second cohomology, capturing the Hodge structures on smooth cubics. The map is injective on the smooth locus and provides a complex hyperbolic geometry for the moduli.^[44]^[45] Compactifications of the moduli space incorporate singular cubic surfaces, with the GIT quotient serving as one such model where boundary points correspond to semistable cubics with mild singularities like nodes, obtained via blow-downs along exceptional curves resolving those singularities. Alternative compactifications, such as the Baily-Borel compactification of the ball quotient or toroidal compactifications, are isomorphic to the GIT model over the smooth locus but differ birationally in the boundary, including strata for more degenerate cases. Recent work has explored non-isomorphic smooth compactifications, such as Kirwan blowups versus toroidal ones, highlighting their distinct birational geometries while preserving cohomology.^[46]^[47]

Cone of Curves

The Néron–Severi lattice of a smooth cubic surface

X \subset \mathbb{P}^3_k

over an algebraically closed field

k

has rank 7 and is generated by the class of a plane section

C

(the hyperplane class) together with the classes of six disjoint lines

C_1, \dots, C_6

X

, or equivalently by the classes of all 27 lines on

X

.^[48]^[49] The intersection form on this lattice is hyperbolic, with signature

(1,6)

, meaning one positive eigenvalue and six negative eigenvalues under the quadratic form defined via the Euler characteristic

\chi(X, \sum m_i D_i)

.^[48] The cone of curves

\overline{\mathrm{NE}}^1(X)

is the dual to the ample cone in the Néron–Severi space and is the closure of the cone generated by effective 1-cycles. For a smooth cubic surface, it is polyhedral and generated by the 27 extremal rays corresponding to the classes of the 27 lines on

X

.^[48] These rays are all

K_X

-negative, where

K_X = -C

is the canonical class, confirming that the Mori cone

\overline{\mathrm{NE}}_1(X)

coincides with

\overline{\mathrm{NE}}^1(X)

.^[48] Contractions of extremal faces of the Mori cone yield birational maps to lower-dimensional varieties. For instance, the face generated by the classes of six disjoint lines

\sum_{i=1}^6 \mathbb{R}^+ [C_i]

contracts to

\mathbb{P}^2_k

, realizing

X

as the blow-up of

\mathbb{P}^2_k

at six points (a del Pezzo surface of degree 3).^[48] Other extremal faces contract to del Pezzo surfaces of higher degree or to ruled surfaces, such as

\mathbb{P}^1 \times \mathbb{P}^1

, depending on the configuration of lines in the face.^[48] For singular cubic surfaces, the structure of the cone of curves differs due to the reduced Picard rank and altered line configurations, but the extremal rays remain tied to lines or exceptional curves resolving singularities.

Info Pages

Talk Pages

Special Pages

Cubic surface

Recent from talks

Recent from talks

Contribute something

Contribute something

Media Pages

Timelines

Articles

Notes collections

Notes

Notes

Days in Chronicle

Cubic surface

Cubic surface

Fundamentals

Definition and General Form

Smoothness and Projective Embedding

Geometric Features

The 27 Lines

Blow-up Realization

Algebraic Properties

Rationality

Automorphisms of Smooth Cubics

Singular Cases

Classification of Singularities

Lines on Singular Cubics

Automorphism Groups of Singular Cubics

Variations over Fields

Real Cubic Surfaces

Cubic Surfaces over Arbitrary Fields

Advanced Structures

Moduli Space

Cone of Curves

References

Add your contribution

Related Hubs

Contribute something

History

Media collections

Cubic surface

Recent from talks

Recent from talks

Contribute something

Contribute something

Media Pages

Timelines

Articles

Notes collections

Notes

Notes

Days in Chronicle

Cubic surface

Cubic surface

Fundamentals

Definition and General Form

Smoothness and Projective Embedding

Geometric Features

The 27 Lines

Blow-up Realization

Algebraic Properties

Rationality

Automorphisms of Smooth Cubics

Singular Cases

Classification of Singularities

Add your contribution

Related Hubs

Contribute something