Hubbry Logo
Dual graphDual graphMain
Open search
Dual graph
Community hub
Dual graph
logo
8 pages, 0 posts
0 subscribers
Be the first to start a discussion here.
Be the first to start a discussion here.
Contribute something
Dual graph
Dual graph
Dual graph
View on Wikipedia
from Wikipedia

The red graph is the dual graph of the blue graph, and vice versa.

In the mathematical discipline of graph theory, the dual graph of a planar graph G is a graph that has a vertex for each face of G. The dual graph has an edge for each pair of faces in G that are separated from each other by an edge, and a self-loop when the same face appears on both sides of an edge. Thus, each edge e of G has a corresponding dual edge, whose endpoints are the dual vertices corresponding to the faces on either side of e. The definition of the dual depends on the choice of embedding of the graph G, so it is a property of plane graphs (graphs that are already embedded in the plane) rather than planar graphs (graphs that may be embedded but for which the embedding is not yet known). For planar graphs generally, there may be multiple dual graphs, depending on the choice of planar embedding of the graph.

Historically, the first form of graph duality to be recognized was the association of the Platonic solids into pairs of dual polyhedra. Graph duality is a topological generalization of the geometric concepts of dual polyhedra and dual tessellations, and is in turn generalized combinatorially by the concept of a dual matroid. Variations of planar graph duality include a version of duality for directed graphs, and duality for graphs embedded onto non-planar two-dimensional surfaces.

These notions of dual graphs should not be confused with a different notion, the edge-to-vertex dual or line graph of a graph.

The term dual is used because the property of being a dual graph is symmetric, meaning that if H is a dual of a connected graph G, then G is a dual of H. When discussing the dual of a graph G, the graph G itself may be referred to as the "primal graph". Many other graph properties and structures may be translated into other natural properties and structures of the dual. For instance, cycles are dual to cuts, spanning trees are dual to the complements of spanning trees, and simple graphs (without parallel edges or self-loops) are dual to 3-edge-connected graphs.

Graph duality can help explain the structure of mazes and of drainage basins. Dual graphs have also been applied in computer vision, computational geometry, mesh generation, and the design of integrated circuits.

Examples

[edit]

Cycles and dipoles

[edit]
A dipole graph
A cycle graph

The unique planar embedding of a cycle graph divides the plane into only two regions, the inside and outside of the cycle, by the Jordan curve theorem. However, in an n-cycle, these two regions are separated from each other by n different edges. Therefore, the dual graph of the n-cycle is a multigraph with two vertices (dual to the regions), connected to each other by n dual edges. Such a graph is called a multiple edge, linkage, or sometimes a dipole graph. Conversely, the dual to an n-edge dipole graph is an n-cycle.[1]

Dual polyhedra

[edit]
Main article: Dual polyhedron
The cube and regular octahedron are dual graphs of each other

According to Steinitz's theorem, every polyhedral graph (the graph formed by the vertices and edges of a three-dimensional convex polyhedron) must be planar and 3-vertex-connected, and every 3-vertex-connected planar graph comes from a convex polyhedron in this way. Every three-dimensional convex polyhedron has a dual polyhedron; the dual polyhedron has a vertex for every face of the original polyhedron, with two dual vertices adjacent whenever the corresponding two faces share an edge. Whenever two polyhedra are dual, their graphs are also dual. For instance the Platonic solids come in dual pairs, with the octahedron dual to the cube, the dodecahedron dual to the icosahedron, and the tetrahedron dual to itself.[2] Polyhedron duality can also be extended to duality of higher dimensional polytopes,[3] but this extension of geometric duality does not have clear connections to graph-theoretic duality.

Self-dual graphs

[edit]
A self-dual graph.

A plane graph is said to be self-dual if it is isomorphic to its dual graph. The wheel graphs provide an infinite family of self-dual graphs coming from self-dual polyhedra (the pyramids).[4][5] However, there also exist self-dual graphs that are not polyhedral, such as the one shown. Servatius & Christopher (1992) describe two operations, adhesion and explosion, that can be used to construct a self-dual graph containing a given planar graph; for instance, the self-dual graph shown can be constructed as the adhesion of a tetrahedron with its dual.[5]

It follows from Euler's formula that every self-dual graph with n vertices has exactly 2n − 2 edges.[6] Every simple self-dual planar graph contains at least four vertices of degree three, and every self-dual embedding has at least four triangular faces.[7]

Properties

[edit]

Many natural and important concepts in graph theory correspond to other equally natural but different concepts in the dual graph. Because the dual of the dual of a connected plane graph is isomorphic to the primal graph,[8] each of these pairings is bidirectional: if concept X in a planar graph corresponds to concept Y in the dual graph, then concept Y in a planar graph corresponds to concept X in the dual.

Simple graphs versus multigraphs

[edit]

The dual of a simple graph need not be simple: it may have self-loops (an edge with both endpoints at the same vertex) or multiple edges connecting the same two vertices, as was already evident in the example of dipole multigraphs being dual to cycle graphs. As a special case of the cut-cycle duality discussed below, the bridges of a planar graph G are in one-to-one correspondence with the self-loops of the dual graph.[9] For the same reason, a pair of parallel edges in a dual multigraph (that is, a length-2 cycle) corresponds to a 2-edge cutset in the primal graph (a pair of edges whose deletion disconnects the graph). Therefore, a planar graph is simple if and only if its dual has no 1- or 2-edge cutsets; that is, if it is 3-edge-connected. The simple planar graphs whose duals are simple are exactly the 3-edge-connected simple planar graphs.[10] This class of graphs includes, but is not the same as, the class of 3-vertex-connected simple planar graphs. For instance, the figure showing a self-dual graph is 3-edge-connected (and therefore its dual is simple) but is not 3-vertex-connected.

Uniqueness

[edit]
Two red graphs are duals for the blue one, but they are not isomorphic.

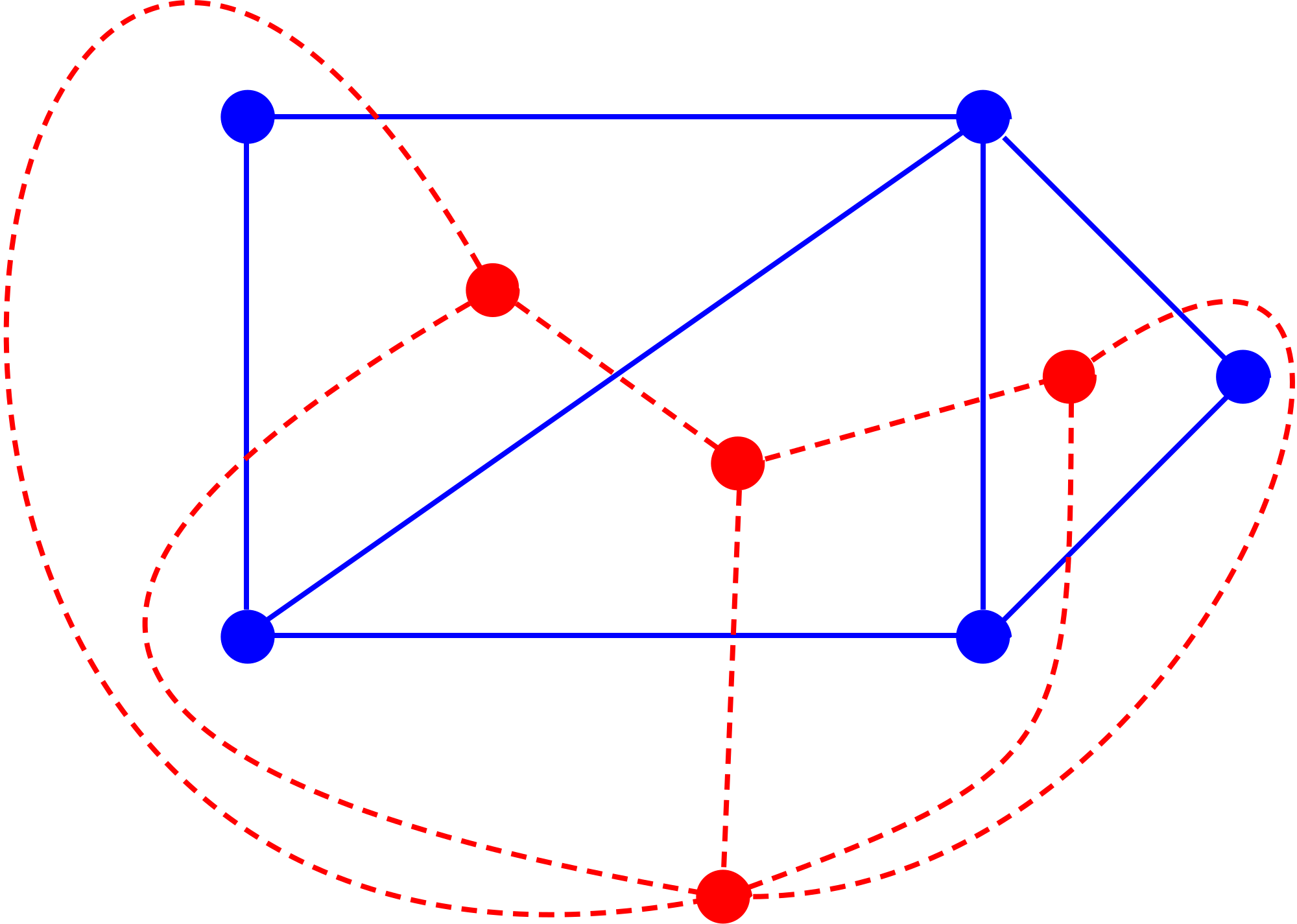
Because the dual graph depends on a particular embedding, the dual graph of a planar graph is not unique, in the sense that the same planar graph can have non-isomorphic dual graphs.[11] In the picture, the blue graphs are isomorphic but their dual red graphs are not. The upper red dual has a vertex with degree 6 (corresponding to the outer face of the blue graph) while in the lower red graph all degrees are less than 6.

Hassler Whitney showed that if the graph is 3-connected then the embedding, and thus the dual graph, is unique.[12] By Steinitz's theorem, these graphs are exactly the polyhedral graphs, the graphs of convex polyhedra. A planar graph is 3-vertex-connected if and only if its dual graph is 3-vertex-connected. Moreover, a planar biconnected graph has a unique embedding, and therefore also a unique dual, if and only if it is a subdivision of a 3-vertex-connected planar graph (a graph formed from a 3-vertex-connected planar graph by replacing some of its edges by paths).[13] For some planar graphs that are not 3-vertex-connected, such as the complete bipartite graph K2,4, the embedding is not unique, but all embeddings are isomorphic. When this happens, correspondingly, all dual graphs are isomorphic.

Because different embeddings may lead to different dual graphs, testing whether one graph is a dual of another (without already knowing their embeddings) is a nontrivial algorithmic problem. For biconnected graphs, it can be solved in polynomial time by using the SPQR trees of the graphs to construct a canonical form for the equivalence relation of having a shared mutual dual. For instance, the two red graphs in the illustration are equivalent according to this relation. However, for planar graphs that are not biconnected, this relation is not an equivalence relation and the problem of testing mutual duality is NP-complete.[14]

Cuts and cycles

[edit]

A cutset in an arbitrary connected graph is a subset of edges defined from a partition of the vertices into two subsets, by including an edge in the subset when it has one endpoint on each side of the partition. Removing the edges of a cutset necessarily splits the graph into at least two connected components. A minimal cutset (also called a bond) is a cutset with the property that every proper subset of the cutset is not itself a cut. A minimal cutset of a connected graph necessarily separates its graph into exactly two components, and consists of the set of edges that have one endpoint in each component.[15] A simple cycle is a connected subgraph in which each vertex of the cycle is incident to exactly two edges of the cycle.[16]

In a connected planar graph G, every simple cycle of G corresponds to a minimal cutset in the dual of G, and vice versa.[17] This can be seen as a form of the Jordan curve theorem: each simple cycle separates the faces of G into the faces in the interior of the cycle and the faces of the exterior of the cycle, and the duals of the cycle edges are exactly the edges that cross from the interior to the exterior.[18] The girth of any planar graph (the size of its smallest cycle) equals the edge connectivity of its dual graph (the size of its smallest cutset).[19]

This duality extends from individual cutsets and cycles to vector spaces defined from them. The cycle space of a graph is defined as the family of all subgraphs that have even degree at each vertex; it can be viewed as a vector space over the two-element finite field, with the symmetric difference of two sets of edges acting as the vector addition operation in the vector space. Similarly, the cut space of a graph is defined as the family of all cutsets, with vector addition defined in the same way. Then the cycle space of any planar graph and the cut space of its dual graph are isomorphic as vector spaces.[20] Thus, the rank of a planar graph (the dimension of its cut space) equals the cyclotomic number of its dual (the dimension of its cycle space) and vice versa.[11] A cycle basis of a graph is a set of simple cycles that form a basis of the cycle space (every even-degree subgraph can be formed in exactly one way as a symmetric difference of some of these cycles). For edge-weighted planar graphs (with sufficiently general weights that no two cycles have the same weight) the minimum-weight cycle basis of the graph is dual to the Gomory–Hu tree of the dual graph, a collection of nested cuts that together include a minimum cut separating each pair of vertices in the graph. Each cycle in the minimum weight cycle basis has a set of edges that are dual to the edges of one of the cuts in the Gomory–Hu tree. When cycle weights may be tied, the minimum-weight cycle basis may not be unique, but in this case it is still true that the Gomory–Hu tree of the dual graph corresponds to one of the minimum weight cycle bases of the graph.[20]

In directed planar graphs, simple directed cycles are dual to directed cuts (partitions of the vertices into two subsets such that all edges go in one direction, from one subset to the other). Strongly oriented planar graphs (graphs whose underlying undirected graph is connected, and in which every edge belongs to a cycle) are dual to directed acyclic graphs in which no edge belongs to a cycle. To put this another way, the strong orientations of a connected planar graph (assignments of directions to the edges of the graph that result in a strongly connected graph) are dual to acyclic orientations (assignments of directions that produce a directed acyclic graph).[21] In the same way, dijoins (sets of edges that include an edge from each directed cut) are dual to feedback arc sets (sets of edges that include an edge from each cycle).[22]

Spanning trees

[edit]
A simple maze in which the maze walls and the free space between the walls form two interdigitating trees

A spanning tree may be defined as a set of edges that, together with all of the vertices of the graph, forms a connected and acyclic subgraph. But, by cut-cycle duality, if a set S of edges in a planar graph G is acyclic (has no cycles), then the set of edges dual to S has no cuts, from which it follows that the complementary set of dual edges (the duals of the edges that are not in S) forms a connected subgraph. Symmetrically, if S is connected, then the edges dual to the complement of S form an acyclic subgraph. Therefore, when S has both properties – it is connected and acyclic – the same is true for the complementary set in the dual graph. That is, each spanning tree of G is complementary to a spanning tree of the dual graph, and vice versa. Thus, the edges of any planar graph and its dual can together be partitioned (in multiple different ways) into two spanning trees, one in the primal and one in the dual, that together extend to all the vertices and faces of the graph but never cross each other. In particular, the minimum spanning tree of G is complementary to the maximum spanning tree of the dual graph.[23] However, this does not work for shortest path trees, even approximately: there exist planar graphs such that, for every pair of a spanning tree in the graph and a complementary spanning tree in the dual graph, at least one of the two trees has distances that are significantly longer than the distances in its graph.[24]

An example of this type of decomposition into interdigitating trees can be seen in some simple types of mazes, with a single entrance and no disconnected components of its walls. In this case both the maze walls and the space between the walls take the form of a mathematical tree. If the free space of the maze is partitioned into simple cells (such as the squares of a grid) then this system of cells can be viewed as an embedding of a planar graph, in which the tree structure of the walls forms a spanning tree of the graph and the tree structure of the free space forms a spanning tree of the dual graph.[25] Similar pairs of interdigitating trees can also be seen in the tree-shaped pattern of streams and rivers within a drainage basin and the dual tree-shaped pattern of ridgelines separating the streams.[26]

This partition of the edges and their duals into two trees leads to a simple proof of Euler’s formula V − E + F = 2 for planar graphs with V vertices, E edges, and F faces. Any spanning tree and its complementary dual spanning tree partition the edges into two subsets of V − 1 and F − 1 edges respectively, and adding the sizes of the two subsets gives the equation

E = (V − 1) + (F − 1)

which may be rearranged to form Euler's formula. According to Duncan Sommerville, this proof of Euler's formula is due to K. G. C. Von Staudt’s Geometrie der Lage (Nürnberg, 1847).[27]

In nonplanar surface embeddings the set of dual edges complementary to a spanning tree is not a dual spanning tree. Instead this set of edges is the union of a dual spanning tree with a small set of extra edges whose number is determined by the genus of the surface on which the graph is embedded. The extra edges, in combination with paths in the spanning trees, can be used to generate the fundamental group of the surface.[28]

Additional properties

[edit]

Any counting formula involving vertices and faces that is valid for all planar graphs may be transformed by planar duality into an equivalent formula in which the roles of the vertices and faces have been swapped. Euler's formula, which is self-dual, is one example. Another given by Harary involves the handshaking lemma, according to which the sum of the degrees of the vertices of any graph equals twice the number of edges. In its dual form, this lemma states that in a plane graph, the sum of the numbers of sides of the faces of the graph equals twice the number of edges.[29]

The medial graph of a plane graph is isomorphic to the medial graph of its dual. Two planar graphs can have isomorphic medial graphs only if they are dual to each other.[30]

A planar graph with four or more vertices is maximal (no more edges can be added while preserving planarity) if and only if its dual graph is both 3-vertex-connected and 3-regular.[31]

A connected planar graph is Eulerian (has even degree at every vertex) if and only if its dual graph is bipartite.[32] A Hamiltonian cycle in a planar graph G corresponds to a partition of the vertices of the dual graph into two subsets (the interior and exterior of the cycle) whose induced subgraphs are both trees. In particular, Barnette's conjecture on the Hamiltonicity of cubic bipartite polyhedral graphs is equivalent to the conjecture that every Eulerian maximal planar graph can be partitioned into two induced trees.[33]

If a planar graph G has Tutte polynomial TG(x,y), then the Tutte polynomial of its dual graph is obtained by swapping x and y. For this reason, if some particular value of the Tutte polynomial provides information about certain types of structures in G, then swapping the arguments to the Tutte polynomial will give the corresponding information for the dual structures. For instance, the number of strong orientations is TG(0,2) and the number of acyclic orientations is TG(2,0).[34] For bridgeless planar graphs, graph colorings with k colors correspond to nowhere-zero flows modulo k on the dual graph. For instance, the four color theorem (the existence of a 4-coloring for every planar graph) can be expressed equivalently as stating that the dual of every bridgeless planar graph has a nowhere-zero 4-flow. The number of k-colorings is counted (up to an easily computed factor) by the Tutte polynomial value TG(1 − k,0) and dually the number of nowhere-zero k-flows is counted by TG(0,1 − k).[35]

An st-planar graph is a connected planar graph together with a bipolar orientation of that graph, an orientation that makes it acyclic with a single source and a single sink, both of which are required to be on the same face as each other. Such a graph may be made into a strongly connected graph by adding one more edge, from the sink back to the source, through the outer face. The dual of this augmented planar graph is itself the augmentation of another st-planar graph.[36]

Variations

[edit]

Directed graphs

[edit]

In a directed plane graph, the dual graph may be made directed as well, by orienting each dual edge by a 90° clockwise turn from the corresponding primal edge.[36] Strictly speaking, this construction is not a duality of directed planar graphs, because starting from a graph G and taking the dual twice does not return to G itself, but instead constructs a graph isomorphic to the transpose graph of G, the graph formed from G by reversing all of its edges. Taking the dual four times returns to the original graph.

Weak dual

[edit]

The weak dual of a plane graph is the subgraph of the dual graph whose vertices correspond to the bounded faces of the primal graph. A plane graph is outerplanar if and only if its weak dual is a forest. For any plane graph G, let G+ be the plane multigraph formed by adding a single new vertex v in the unbounded face of G, and connecting v to each vertex of the outer face (multiple times, if a vertex appears multiple times on the boundary of the outer face); then, G is the weak dual of the (plane) dual of G+.[37]

Infinite graphs and tessellations

[edit]

The concept of duality applies as well to infinite graphs embedded in the plane as it does to finite graphs. However, care is needed to avoid topological complications such as points of the plane that are neither part of an open region disjoint from the graph nor part of an edge or vertex of the graph. When all faces are bounded regions surrounded by a cycle of the graph, an infinite planar graph embedding can also be viewed as a tessellation of the plane, a covering of the plane by closed disks (the tiles of the tessellation) whose interiors (the faces of the embedding) are disjoint open disks. Planar duality gives rise to the notion of a dual tessellation, a tessellation formed by placing a vertex at the center of each tile and connecting the centers of adjacent tiles.[38]

A Voronoi diagram (red) and Delaunay triangulation (black) of a finite point set (the black points)

The concept of a dual tessellation can also be applied to partitions of the plane into finitely many regions. It is closely related to but not quite the same as planar graph duality in this case. For instance, the Voronoi diagram of a finite set of point sites is a partition of the plane into polygons within which one site is closer than any other. The sites on the convex hull of the input give rise to unbounded Voronoi polygons, two of whose sides are infinite rays rather than finite line segments. The dual of this diagram is the Delaunay triangulation of the input, a planar graph that connects two sites by an edge whenever there exists a circle that contains those two sites and no other sites. The edges of the convex hull of the input are also edges of the Delaunay triangulation, but they correspond to rays rather than line segments of the Voronoi diagram. This duality between Voronoi diagrams and Delaunay triangulations can be turned into a duality between finite graphs in either of two ways: by adding an artificial vertex at infinity to the Voronoi diagram, to serve as the other endpoint for all of its rays,[39] or by treating the bounded part of the Voronoi diagram as the weak dual of the Delaunay triangulation. Although the Voronoi diagram and Delaunay triangulation are dual, their embedding in the plane may have additional crossings beyond the crossings of dual pairs of edges. Each vertex of the Delaunay triangle is positioned within its corresponding face of the Voronoi diagram. Each vertex of the Voronoi diagram is positioned at the circumcenter of the corresponding triangle of the Delaunay triangulation, but this point may lie outside its triangle.

Nonplanar embeddings

[edit]
K7 is dual to the Heawood graph in the torus
K6 is dual to the Petersen graph in the projective plane

The concept of duality can be extended to graph embeddings on two-dimensional manifolds other than the plane. The definition is the same: there is a dual vertex for each connected component of the complement of the graph in the manifold, and a dual edge for each graph edge connecting the two dual vertices on either side of the edge. In most applications of this concept, it is restricted to embeddings with the property that each face is a topological disk; this constraint generalizes the requirement for planar graphs that the graph be connected. With this constraint, the dual of any surface-embedded graph has a natural embedding on the same surface, such that the dual of the dual is isomorphic to and isomorphically embedded to the original graph. For instance, the complete graph K7 is a toroidal graph: it is not planar but can be embedded in a torus, with each face of the embedding being a triangle. This embedding has the Heawood graph as its dual graph.[40]

The same concept works equally well for non-orientable surfaces. For instance, K6 can be embedded in the projective plane with ten triangular faces as the hemi-icosahedron, whose dual is the Petersen graph embedded as the hemi-dodecahedron.[41]

Even planar graphs may have nonplanar embeddings, with duals derived from those embeddings that differ from their planar duals. For instance, the four Petrie polygons of a cube (hexagons formed by removing two opposite vertices of the cube) form the hexagonal faces of an embedding of the cube in a torus. The dual graph of this embedding has four vertices forming a complete graph K4 with doubled edges. In the torus embedding of this dual graph, the six edges incident to each vertex, in cyclic order around that vertex, cycle twice through the three other vertices. In contrast to the situation in the plane, this embedding of the cube and its dual is not unique; the cube graph has several other torus embeddings, with different duals.[40]

Many of the equivalences between primal and dual graph properties of planar graphs fail to generalize to nonplanar duals, or require additional care in their generalization.

Another operation on surface-embedded graphs is the Petrie dual, which uses the Petrie polygons of the embedding as the faces of a new embedding. Unlike the usual dual graph, it has the same vertices as the original graph, but generally lies on a different surface.[42] Surface duality and Petrie duality are two of the six Wilson operations, and together generate the group of these operations.[43]

Matroids and algebraic duals

[edit]

An algebraic dual of a connected graph G is a graph G* such that G and G* have the same set of edges, any cycle of G is a cut of G*, and any cut of G is a cycle of G*. Every planar graph has an algebraic dual, which is in general not unique (any dual defined by a plane embedding will do). The converse is actually true, as settled by Hassler Whitney in Whitney's planarity criterion:[44]

A connected graph G is planar if and only if it has an algebraic dual.

The same fact can be expressed in the theory of matroids. If M is the graphic matroid of a graph G, then a graph G* is an algebraic dual of G if and only if the graphic matroid of G* is the dual matroid of M. Then Whitney's planarity criterion can be rephrased as stating that the dual matroid of a graphic matroid M is itself a graphic matroid if and only if the underlying graph G of M is planar. If G is planar, the dual matroid is the graphic matroid of the dual graph of G. In particular, all dual graphs, for all the different planar embeddings of G, have isomorphic graphic matroids.[45]

For nonplanar surface embeddings, unlike planar duals, the dual graph is not generally an algebraic dual of the primal graph. And for a non-planar graph G, the dual matroid of the graphic matroid of G is not itself a graphic matroid. However, it is still a matroid whose circuits correspond to the cuts in G, and in this sense can be thought of as a combinatorially generalized algebraic dual of G.[46]

The duality between Eulerian and bipartite planar graphs can be extended to binary matroids (which include the graphic matroids derived from planar graphs): a binary matroid is Eulerian if and only if its dual matroid is bipartite.[32]

The two dual concepts of girth and edge connectivity are unified in matroid theory by matroid girth: the girth of the graphic matroid of a planar graph is the same as the graph's girth, and the girth of the dual matroid (the graphic matroid of the dual graph) is the edge connectivity of the graph.[19]

Applications

[edit]

Along with its use in graph theory, the duality of planar graphs has applications in several other areas of mathematical and computational study.

In geographic information systems, flow networks (such as the networks showing how water flows in a system of streams and rivers) are dual to cellular networks describing drainage divides. This duality can be explained by modeling the flow network as a spanning tree on a grid graph of an appropriate scale, and modeling the drainage divide as the complementary spanning tree of ridgelines on the dual grid graph.[47]

In computer vision, digital images are partitioned into small square pixels, each of which has its own color. The dual graph of this subdivision into squares has a vertex per pixel and an edge between pairs of pixels that share an edge; it is useful for applications including clustering of pixels into connected regions of similar colors.[48]

In computational geometry, the duality between Voronoi diagrams and Delaunay triangulations implies that any algorithm for constructing a Voronoi diagram can be immediately converted into an algorithm for the Delaunay triangulation, and vice versa.[49] The same duality can also be used in finite element mesh generation. Lloyd's algorithm, a method based on Voronoi diagrams for moving a set of points on a surface to more evenly spaced positions, is commonly used as a way to smooth a finite element mesh described by the dual Delaunay triangulation. This method improves the mesh by making its triangles more uniformly sized and shaped.[50]

In the synthesis of CMOS circuits, the function to be synthesized is represented as a formula in Boolean algebra. Then this formula is translated into two series–parallel multigraphs. These graphs can be interpreted as circuit diagrams in which the edges of the graphs represent transistors, gated by the inputs to the function. One circuit computes the function itself, and the other computes its complement. One of the two circuits is derived by converting the conjunctions and disjunctions of the formula into series and parallel compositions of graphs, respectively. The other circuit reverses this construction, converting the conjunctions and disjunctions of the formula into parallel and series compositions of graphs.[51] These two circuits, augmented by an additional edge connecting the input of each circuit to its output, are planar dual graphs.[52]

History

[edit]

The duality of convex polyhedra was recognized by Johannes Kepler in his 1619 book Harmonices Mundi.[53] Recognizable planar dual graphs, outside the context of polyhedra, appeared as early as 1725, in Pierre Varignon's posthumously published work, Nouvelle Méchanique ou Statique. This was even before Leonhard Euler's 1736 work on the Seven Bridges of Königsberg that is often taken to be the first work on graph theory. Varignon analyzed the forces on static systems of struts by drawing a graph dual to the struts, with edge lengths proportional to the forces on the struts; this dual graph is a type of Cremona diagram.[54] In connection with the four color theorem, the dual graphs of maps (subdivisions of the plane into regions) were mentioned by Alfred Kempe in 1879, and extended to maps on non-planar surfaces by Lothar Heffter [de] in 1891.[55] Duality as an operation on abstract planar graphs was introduced by Hassler Whitney in 1931.[56]

Notes

[edit]
[edit]
Revisions and contributorsEdit on WikipediaRead on Wikipedia

Dual graph

View on Grokipedia
from Grokipedia
In , the dual graph of a plane of a connected GG is an auxiliary graph G∗G^* whose vertices correspond to the faces of GG, with an edge in G∗G^* joining two vertices if and only if the corresponding faces in GG share a boundary edge. This construction, which depends on the specific of GG, preserves the number of edges such that ∣E(G∗)∣=∣E(G)∣|E(G^*)| = |E(G)|, while the number of vertices in G∗G^* equals the number of faces in GG, and the number of faces in G∗G^* equals the number of vertices in GG. Key properties of dual graphs include the equality of degrees between a face in GG and its corresponding vertex in G∗G^*, ensuring that the dual captures the adjacency structure of faces. For polyhedral graphs, the dual is unique up to , and both the primal and dual satisfy v−e+f=2v - e + f = 2. Cycles in GG correspond to bonds (minimal edge cuts) in G∗G^*, and vice versa, establishing an isomorphism between the cycle space of GG and the bond space of G∗G^*. The concept was formalized in the early , with H. Whitney proving in 1932 that geometric and combinatorial duals coincide for 3-connected planar graphs. Dual graphs play a central role in planar graph theory, facilitating proofs of structural theorems and enabling applications such as map coloring—where coloring countries on a map reduces to vertex coloring the dual graph—and modeling spatial relationships in fields like transportation networks and RNA secondary structures. Self-dual graphs, which are isomorphic to their own duals, represent special cases with symmetric embeddings, such as certain wheel graphs. The duality extends to infinite planar graphs and tessellations, broadening its utility in combinatorial geometry.

Fundamentals

Definition

In , the dual graph of a GG embedded in the plane is a graph G∗G^* whose vertices correspond one-to-one with the faces of GG, including the unbounded outer face. An edge exists in G∗G^* between two vertices the corresponding faces in GG share a boundary edge in the embedding; each such shared edge in GG corresponds uniquely to an edge in G∗G^*, ensuring that the number of edges in G∗G^* equals the number of edges in GG. This construction depends on the specific planar embedding of GG, as different embeddings may yield non- dual graphs, though for 3-connected s, the dual is unique up to . The dual graph interchanges the roles of vertices and faces in the primal graph GG: the number of vertices in G∗G^* equals the number of faces in GG (denoted ∣V∗∣=∣F∣|V^*| = |F|), and the number of faces in G∗G^* equals the number of vertices in GG (denoted ∣F∗∣=∣V∣|F^*| = |V|. Loops and multiple edges in GG transform into edges in G∗G^* and vice versa, preserving the total edge count ∣E∗∣=∣E∣|E^*| = |E|. For polyhedral graphs—those realizable as the 1-skeletons of convex polyhedra—the dual corresponds to the graph of the polyhedron's faces, satisfying V−E+F=2V - E + F = 2 in both primal and dual forms. The concept of the dual graph was formalized combinatorially by Whitney, who showed that for 3-connected s, the combinatorial dual (defined via incidence relations) coincides with the geometric dual (derived from a plane ), establishing a foundational duality in planar graph theory. This duality extends to multigraphs and allows the dual of the dual to recover the original graph, up to the .

Construction

The dual graph of a connected plane graph G=(V,E)G = (V, E) is a G∗=(V∗,E∗)G^* = (V^*, E^*) constructed as follows: the vertex set V∗V^* consists of one vertex vf∗v_f^* for each face ff of the embedding of GG, including the unbounded outer face. For each edge e∈Ee \in E of GG, which separates two faces ff and gg (possibly the same face if ee is a loop or bridge), add an edge e∗∈E∗e^* \in E^* in G∗G^* connecting vf∗v_f^* and vg∗v_g^*; if f=gf = g, this results in a loop at vf∗v_f^*. Geometrically, this can be realized by placing each vertex vf∗v_f^* in the interior of face ff and drawing edge e∗e^* as a that crosses ee transversely once and does not intersect any other edges of GG except at endpoints. This construction ensures a natural between the edges of GG and G∗G^*, preserving the incidence structure between faces and edges. The resulting G∗G^* may contain multiple edges between the same pair of vertices if the corresponding faces in GG share multiple edges, and loops arise from bridges or loops in GG. the dual of G∗G^* recovers GG, establishing a mutual duality. Combinatorially, the construction can also be defined using the rotation system of the : vertices of G∗G^* correspond to faces, and the cyclic order around each primal vertex induces the dual's structure, ensuring the embedding of G∗G^* reflects the primal's facial boundaries. This approach, formalized by Whitney, guarantees that a graph admits such a dual construction if and only if it is planar.

Examples

Cycles and dipoles

In planar graph theory, the relationship between cycles in a primal graph and structures in its dual graph highlights a fundamental duality. A simple cycle in the primal embedding separates the plane into an interior region and an exterior region, each constituting a face. The dual graph places a vertex for each such face and includes an edge for every primal edge bounding both faces. Thus, for an nn-cycle CnC_n embedded in the plane, all nn primal edges lie between the two faces, resulting in nn parallel edges connecting the two corresponding dual vertices. This configuration forms a dipole subgraph in the dual. A dipole graph DnD_n, also known as a linkage or , is defined as a with exactly two vertices joined by nn parallel edges, where n≥1n \geq 1. The plane dual of the CnC_n is precisely the dipole graph DnD_n. Conversely, the dual of DnD_n—embedded such that its multiple edges bound a single interior face—is the CnC_n. This reciprocity arises because the two vertices of DnD_n represent the interior and exterior faces, while the nn parallel edges correspond to the nn edges of the bounding cycle in the primal. In a more general planar embedding of a graph GG, a simple cycle that serves as the shared boundary between exactly two faces f1f_1 and f2f_2 induces a subgraph in the dual G∗G^* between the vertices representing f1f_1 and f2f_2. If the cycle has length kk, the induced has kk parallel edges. This property underscores the correspondence between cycles (minimal circuits enclosing a region) in the primal and minimal cut-sets (bonds separating two faces) in the dual, where the multiplicity reflects the cycle's length. For instance, consider a containing a 4-cycle bounding two adjacent faces; its dual includes a D4D_4 between the respective face-vertices. Dipoles also appear in topological graph theory when studying embeddings on surfaces, such as in genus distributions, where DnD_n serves as a building block for analyzing voltage graphs and covering spaces. However, in the strict planar case, they primarily illustrate the local duality around separating cycles, providing insight into face adjacencies without altering global connectivity.

Polyhedral duals

In , the dual graph of a is defined by creating a vertex for each face of the polyhedron and placing an edge between two vertices if the corresponding faces share a boundary edge in the polyhedron. This construction applies specifically to polyhedral graphs, which are the 1-skeleton graphs of convex polyhedra and, by Steinitz's theorem, are precisely the simple 3-connected planar graphs. The resulting dual graph inherits the combinatorial structure of the polyhedron's faces, transforming face incidences into vertex adjacencies. For polyhedral graphs, the dual is unique because 3-connected planar graphs admit a unique on the sphere up to , ensuring a canonical choice of faces for duality. This uniqueness stems from Whitney's theorem on the rigidity of embeddings for such graphs. Moreover, the dual graph of a polyhedral graph is itself polyhedral, as the geometric —obtained by interchanging vertices and face centers—yields another convex whose 1-skeleton is the dual graph. Both the primal and dual satisfy V−E+F=2V - E + F = 2, where the dual has V∗=FV^* = F, E∗=EE^* = E, and F∗=VF^* = V. The edge degrees in the dual graph correspond to the face sizes of the original : a face with kk sides becomes a vertex of degree kk in the dual. Conversely, the vertex degrees in the primal become the face sizes in the dual . This reciprocity preserves planarity and 3-connectivity, ensuring the dual remains embeddable as a polyhedral graph. Classic examples illustrate these dual pairs among the Platonic solids. The , with 8 triangular faces, 12 edges, and 6 square faces, has a dual graph that is the 1-skeleton of the , featuring 6 vertices (one per cube face), 12 edges, and 8 triangular faces. Similarly, the (20 vertices, 30 edges, 12 pentagonal faces) is dual to the (12 vertices, 30 edges, 20 triangular faces), where each pentagon center of the dodecahedron connects to form the icosahedron's vertices. The is self-dual in this sense, as its four triangular faces yield another tetrahedral graph upon duality.
Primal PolyhedronVertices (V)Edges (E)Faces (F)Dual PolyhedronVertex Degrees in Dual
8126All degree 4
203012All degree 5
464All degree 3
This table highlights the in Euler characteristics and degree sequences for these regular cases. Beyond regulars, duals extend to Archimedean solids and other convex polyhedra, maintaining the polyhedral property.

Self-dual graphs

A self-dual graph is a that is isomorphic to its dual graph. More precisely, in the context of plane embeddings, graph self-duality refers to an between the primal graph G=(V,E)G = (V, E) and its dual G∗=(F∗,E∗)G^* = (F^*, E^*), where vertices of G∗G^* correspond to faces of GG and edges are preserved in incidence. This implies that the number of vertices equals the number of faces, so by for connected plane graphs, v−e+f=2v - e + f = 2 yields e=2v−2e = 2v - 2. Additionally, the degree sequence of vertices in GG matches the face degrees in GG, reflecting the between vertices and faces. Wheel graphs provide a classic family of self-dual plane graphs. The wheel graph WnW_n (with n≥3n \geq 3 rim vertices plus a central hub) has n+1n+1 vertices, 2n2n edges, and n+1n+1 faces (nn triangles and one outer nn-gon). Its dual is isomorphic to WnW_n, as the central vertex in the dual corresponds to the outer face, rim vertices to triangular faces, and edges map accordingly. The tetrahedral graph K4K_4 (equivalent to W3W_3) is the smallest such example, representing the 1-skeleton of a regular , which is map self-dual under its natural . Other examples include certain polyhedral graphs, such as those of self-dual polyhedra like square pyramids, where the primal and dual share the same combinatorial structure. Self-duality manifests in three related but distinct forms for planar graphs: map self-duality ( preserving the ), graph self-duality ( at the graph level), and matroid self-duality ( of cycle and cocycle s). Map self-duality implies the others, but the converses do not hold in general; however, for 3-connected graphs, all forms coincide due to unique embeddings by Steinitz's theorem. A key result is that every 2-connected self-dual matroid admits a self-dual plane , allowing decomposition via 2-sums of irreducible self-dual maps. These properties underpin applications in enumerating self-dual polyhedra and analyzing planar map symmetries, with the number of 3-connected self-dual polyhedral graphs on nn vertices following the sequence 1 (for n=4n=4), 1 (n=5n=5), 2 (n=6n=6), growing to 1908 for n=15n=15.

Properties

Primal-dual relationships

In the context of planar graphs, the primal graph GG and its dual G∗G^* exhibit a fundamental structural correspondence. The vertices of G∗G^* are in one-to-one correspondence with the faces of GG, including the outer face; the edges of G∗G^* correspond bijectively to the edges of GG, with each edge in G∗G^* connecting the vertices representing the two faces adjacent to the corresponding edge in GG; and the faces of G∗G^* correspond to the vertices of GG, where the faces incident to a vertex in G∗G^* represent the faces of GG incident to the corresponding vertex in GG. This construction ensures that the dual operation reverses the roles of vertices and faces while preserving the edge set in , i.e., ∣E(G∗)∣=∣E(G)∣|E(G^*)| = |E(G)|. A key property arising from this correspondence is the application of to both graphs. For a connected plane graph GG, states v(G)−e(G)+f(G)=2v(G) - e(G) + f(G) = 2, where vv, ee, and ff denote the numbers of vertices, edges, and faces, respectively. Substituting the dual relations v(G∗)=f(G)v(G^*) = f(G), e(G∗)=e(G)e(G^*) = e(G), and f(G∗)=v(G)f(G^*) = v(G) yields v(G∗)−e(G∗)+f(G∗)=2v(G^*) - e(G^*) + f(G^*) = 2, confirming that the dual also satisfies . This duality extends to multigraphs, where bridges in the primal become loops in the dual, and loops in the primal become bridges in the dual. The dual of the dual recovers the original graph up to , establishing a symmetric involution: (G∗)∗≅G(G^*)^* \cong G. For 3-connected planar graphs, Whitney proved that the combinatorial dual (defined via rank and nullity relations, where the rank of the primal equals the nullity of the dual and vice versa) coincides with the geometric dual derived from any planar embedding, ensuring uniqueness up to . If the primal is bridgeless, the dual has no loops and is 2-edge-connected (though it may have multiple edges if the primal has 2-edge cuts). These relationships underpin the combinatorial characterization of planarity: a graph admits a dual if and only if it is planar. In terms of connectivity, non-separability (2-vertex-connectivity) in the primal implies non-separability in the dual. For plane multigraphs, multiple may yield non-isomorphic unless the primal is 3-connected, in which case all produce the same combinatorial dual. These primal-dual symmetries facilitate analyses in and duality, where the cycle of the primal is the bond of the dual.

Cuts, cycles, and flows

In , the cycle space of a GG and the cut space (also known as the bond space) of its dual graph G∗G^* are intimately related, forming a foundational aspect of primal-dual duality. The cycle space C(G)C(G) is the over F2\mathbb{F}_2 (the field with two elements) generated by the edge sets of all cycles in GG, with dimension ∣E(G)∣−∣V(G)∣+c(G)|E(G)| - |V(G)| + c(G), where c(G)c(G) denotes the number of connected components of GG. Conversely, the cut space B(G)B(G) is the over F2\mathbb{F}_2 generated by the edge sets of all cuts in GG, where a cut is the set of edges with endpoints in distinct parts of a bipartition of V(G)V(G); its dimension is ∣V(G)∣−c(G)|V(G)| - c(G). These spaces are orthogonal complements in the edge space F2E(G)\mathbb{F}_2^{E(G)}: C(G)=B(G)⊥C(G) = B(G)^\perp and B(G)=C(G)⊥B(G) = C(G)^\perp, meaning their intersection is trivial and they span the full edge space. For a plane graph GG, the dual graph G∗G^* induces a precise correspondence between these structures. Every cycle in GG corresponds to a bond (a minimal nonempty cut) in G∗G^*, as the edges of the cycle bound a set of faces whose vertex set in G∗G^* induces a cut whose minimal edges form the bond. Symmetrically, every bond in GG corresponds to a cycle in G∗G^*, since the edges incident to a vertex partition in GG enclose a cycle of faces in the . This duality extends to the full spaces: the cycle space C(G)C(G) of the primal is precisely the cut space B(G∗)B(G^*) of the dual, and vice versa, C(G∗)=B(G)C(G^*) = B(G). Consequently, properties like the existence of or cut bases transfer between primal and dual, enabling algorithmic and structural insights; for instance, generating a in GG is equivalent to generating a cut basis in G∗G^*. Flows in planar graphs further illuminate this duality through connections to colorings and network capacities. A kk-flow in GG—an orientation and assignment of integers from {−(k−1),…,k−1}\{-(k-1), \dots, k-1\} to edges such that the net flow at each vertex is zero—corresponds to a kk-edge-coloring of G∗G^*, where the coloring respects the dual's edge incidences. More precisely, the chromatic index χ′(G∗)\chi'(G^*) equals the flow number ϕ(G)\phi(G), the minimum kk admitting a nowhere-zero kk-flow in GG. This flow-coloring duality, established by Tutte, implies that maximum flow problems in GG (governed by min-cuts via the ) relate to shortest cycles in G∗G^*, as the capacity of a min-cut in GG equals the length of the shortest separating cycle in G∗G^*. In practice, this allows efficient computation of flows in planar networks by reducing to cycle-finding in the dual, with applications in optimization and embedding problems.

Spanning trees and bonds

In planar graph theory, a fundamental duality exists between spanning trees of a graph GG and those of its dual G∗G^*. Specifically, if TT is a of the connected plane graph GG, then the set of edges in GG not belonging to TT, denoted T‾\overline{T}, corresponds under the natural between edges of GG and G∗G^* to a T‾∗\overline{T}^* of G∗G^*. This correspondence arises because the number of edges in T‾\overline{T} is ∣E(G)∣−(∣V(G)∣−1)=∣E(G)∣−∣V(G)∣+1|E(G)| - (|V(G)| - 1) = |E(G)| - |V(G)| + 1, which equals the required number for a spanning tree in G∗G^* by for connected planar graphs, where ∣V(G∗)∣=∣F(G)∣=∣E(G)∣−∣V(G)∣+2|V(G^*)| = |F(G)| = |E(G)| - |V(G)| + 2. This bijection ensures that every of GG pairs with a unique of G∗G^*, and vice versa, establishing a one-to-one correspondence between the spanning trees of GG and G∗G^*. In the planar embedding, the primal TT and its dual counterpart T‾∗\overline{T}^* are non-crossing: no edge of T‾∗\overline{T}^* crosses an edge of TT, as the dual edges corresponding to T‾\overline{T} connect faces separated only by the non-tree edges of GG. This non-intersection property is crucial for applications in algorithms and structural , such as computing the number of spanning trees via the matrix-tree theorem, which applies symmetrically to both GG and G∗G^*. Bonds, defined as minimal nonempty edge cuts in a graph, exhibit a complementary duality with cycles across the primal-dual boundary. In a plane graph GG, every cycle CC of GG corresponds to a bond C∗C^* in G∗G^*, where C∗C^* is the set of dual edges crossing the edges of CC, and this bond is minimal because removing it disconnects the faces bounded by CC. Conversely, every bond BB in GG corresponds to a cycle B∗B^* in G∗G^*. This induces an between the cycle space of GG (the over GF(2) generated by the cycles of GG) and the bond space of G∗G^* (generated by the bonds of G∗G^*), with equal to ∣E(G)∣−∣V(G)∣+1|E(G)| - |V(G)| + 1. The interplay between spanning trees and bonds is mediated through matroid duality: the graphic matroid of GG, whose bases are the spanning trees of GG, has dual matroid equal to the graphic matroid of G∗G^* for planar GG. Thus, the complement of a spanning tree basis in the matroid of GG is a basis (spanning tree) in the matroid of G∗G^*, while the circuits of the dual matroid correspond to the bonds (minimal cuts) of GG. For instance, in a CnC_n, any spanning tree consists of n−1n-1 edges forming a path, and its complement is a single edge, which dualizes to a spanning tree in the dual; the minimal bonds in CnC_n consist of two edges, dualizing to 2-cycles in the dual. This structure underpins results in network flows and rigidity theory, where primal spanning trees define tree packings and dual bonds enforce connectivity constraints.

Uniqueness and embeddings

The dual graph of a is inherently tied to a specific plane , meaning that the same abstract can admit multiple non-equivalent embeddings, each potentially yielding a distinct dual graph up to . For instance, a graph with a separable structure, such as one containing articulation points, may allow rotations or flips in its embedding that alter the adjacency of faces, resulting in different dual structures. This dependence on the embedding underscores that the dual is not an intrinsic property of the graph alone but rather of its realization in the plane. A pivotal result addressing this non-uniqueness is Whitney's theorem, which establishes that every 3-connected possesses a unique combinatorial in the plane, up to equivalence (including reflections and choice of outer face). In a combinatorial , the of edges around each vertex is fixed, and for 3-connected graphs, this order is invariant across all possible plane realizations, preventing variations that could lead to differing face adjacencies. Consequently, the dual graph of a 3-connected is unique up to , as any two embeddings produce combinatorially equivalent duals where vertices (faces of the primal) and their connections mirror each other precisely. This uniqueness facilitates the unambiguous study of dual properties in such graphs, such as their connectivity and cycle structures. The implications extend to polyhedral graphs and embeddings on the sphere, where the 3-connectedness condition ensures that the dual corresponds to a canonical polyhedron, with faces of the primal becoming vertices of the dual in a fixed manner. Graphs that are subdivisions of 3-connected planar graphs inherit this embedding uniqueness, broadening the class of graphs with well-defined duals independent of embedding choices. However, for graphs lacking 3-connectedness, such as trees or 2-connected but not 3-connected planar graphs, multiple duals remain possible, highlighting the theorem's role in delineating when duality becomes an isomorphism invariant.

Multigraphs versus simple graphs

In , the dual of a plane graph is generally defined as a , allowing for loops and multiple edges, even when the primal graph is simple. This construction ensures that every adjacency between faces in the primal embedding is faithfully represented in the dual, regardless of the primal's structure. For a plane GG, the dual G∗G^* places a vertex in each face of GG (including the outer face) and, for every edge ee of GG, draws an edge e∗e^* in G∗G^* that crosses ee and connects the vertices corresponding to the faces incident with ee. If ee is incident with only one face—such as a loop in GG or a bridge bordered by the same face on both sides—then e∗e^* becomes a loop at that face's vertex. Multiple edges in G∗G^* arise when multiple edges of GG lie between the same pair of faces. Even for simple primal graphs without loops or parallel edges, the dual may still be a . Loops appear in G∗G^* if GG contains a bridge, as the bridge is adjacent to a single face on both sides in the . For instance, consider a simple plane graph consisting of two cycles connected by a single edge (a bridge); the dual will include a loop at the vertex for the outer face (or the relevant shared face) corresponding to that bridge. Multiple edges in G∗G^* occur when two or more edges of the simple GG separate the same two faces, which is possible via a 2-edge cut in GG. An example is the theta graph (Θ\Theta), a simple graph with three paths between two vertices embedded such that two edges bound a digon-like region between two faces, resulting in parallel edges in the dual between the vertices for those faces. The dual of a simple plane graph is itself simple GG has no bridges and no 2-edge cuts, i.e., if GG is 3-edge-connected. In such cases, every edge of GG borders two distinct faces, and no two faces share more than one edge. This property holds notably for 3-connected simple planar graphs, where embeddings are unique up to by Whitney's theorem, ensuring the dual remains simple. In contrast, definitions restricted to simple duals often assume such connectivity conditions on the primal to avoid features.

Variations

Directed dual graphs

In the context of planar graph theory, a directed dual graph arises from a plane digraph, which is a directed graph embedded in the plane without crossings. For a plane digraph DD with underlying undirected plane graph GG, the directed plane dual D∗D^* is constructed such that its vertices correspond to the faces of GG, including the unbounded outer face. Each arc aa in DD induces a corresponding arc a∗a^* in D∗D^*, ensuring a one-to-one correspondence between the arcs of DD and D∗D^*. This construction preserves the planar embedding and introduces directions based on the orientation of the primal arcs relative to the faces they bound. The direction of each dual arc a∗a^* is determined by identifying the faces adjacent to the primal arc aa, traversed from its tail to its head. Specifically, if lal_a is the face lying to the left of aa and rar_a to the right (with respect to the embedding's orientation), then a∗a^* is directed from the vertex representing lal_a to the vertex representing rar_a. In cases where aa is a bridge (cut edge), la=ral_a = r_a, resulting in a loop at the corresponding dual vertex. This left-to-right orientation ensures that the dual digraph reflects the of the embedding, often assuming a counterclockwise traversal around faces for consistency. For undirected primal graphs, a directed dual can be similarly defined by arbitrarily orienting the primal edges or using the embedding's rotation system to assign left/right relations. Key properties of directed dual graphs include their utility in preserving structural relationships between the primal and dual, such as the correspondence between directed cycles in the primal and directed cuts (or bonds) in the dual. In upward planar drawings—where all edges point upward—the directed dual often exhibits acyclicity or specific source-sink structures; for instance, a strongly connected rolling upward on a may have a dual that is a (an acyclic digraph with a single source and ). These graphs are particularly valuable in applications involving flow networks, where primal paths correspond to dual cuts, and in analyzing embeddings on surfaces like , where the dual's connectivity reflects the primal's upward consistency. Directed duals also facilitate duality in generating functions for non-crossing walks, enabling by mapping primal orientations to dual path covers.

Weak and medial duals

In graph theory, the weak dual of a plane graph GG is the subgraph of the dual graph G∗G^* induced by the vertices corresponding to the bounded (internal) faces of GG, excluding the vertex representing the unbounded outer face. This construction preserves adjacencies between bounded faces that share an edge in GG, resulting in a graph that captures the internal structure without the influence of the exterior region. The weak dual is particularly significant for outerplanar graphs: a plane graph is outerplanar if and only if its weak dual is a forest, and for biconnected outerplanar graphs, the weak dual is a tree. This property facilitates analyses of treewidth, pathwidth, and other structural parameters in subclasses of planar graphs. The medial graph (sometimes referred to as a medial dual) of a connected plane graph GG is defined with a vertex for each edge of GG, and an edge between two vertices if the corresponding edges of GG are consecutive around a common face. This yields a 4-regular plane graph embedded along the edges of GG, where each original vertex of degree dd in GG corresponds to a dd-sided face in the medial graph, and each original face of degree kk corresponds to a kk-sided face. Introduced by Ernst Steinitz in 1922 to investigate combinatorial aspects of convex polyhedra, the medial graph encodes both primal and dual information simultaneously. A fundamental property is that the medial graph of GG is isomorphic to the medial graph of its dual G∗G^*, and conversely, two plane graphs are dual if and only if their medial graphs are isomorphic. The medial graph is always Eulerian when all faces of GG have even degree, and it serves as a bridge between line graphs and dual structures, aiding in problems like and equivalence. Weak and medial duals extend the standard dual construction by focusing on bounded regions or edge adjacencies, respectively, and are instrumental in proving duality theorems and characterizing planar embeddings without relying on full dual graphs. For instance, in the medial framework, cycles in the medial graph alternate between vertex and face cycles of the primal, providing a unified view of cuts and flows. These variations are especially valuable in and , where they simplify reductions for algorithms on polyhedral realizations and curve embeddings.

Infinite duals and tessellations

In the context of infinite graphs, a dual graph G∗G^* of an infinite GG is defined such that there exists a between the edges of GG and G∗G^* preserving the cycle space: finite and infinite circuits in GG correspond to minimal cuts (bonds) in G∗G^*, and vice versa. For countable infinite graphs satisfying the condition that no two vertices are joined by infinitely many edge-disjoint paths, the existence of such a dual is equivalent to the graph being planar. This extends the finite case but introduces asymmetries due to potentially infinite circuits, which are handled topologically via the Freudenthal compactification of the graph. Tessellations of the provide a natural setting for infinite dual graphs, where a tessellation G=(V,E,F)G = (V, E, F) is an infinite embedded such that faces are homeomorphic to closed disks, edges lie in exactly two faces, and compact sets are covered by finitely many faces. The dual graph G∗G^* of a tessellation GG has vertices corresponding to faces of GG, with edges between vertices if the faces share an edge in GG; consequently, the faces of G∗G^* correspond to vertices of GG. This duality is bijective across vertices, edges, faces, and corners, preserving degrees: the degree of a vertex in GG equals the degree of the corresponding face in G∗G^*, and vice versa. Moreover, a graph is a tessellation if and only if its dual is, ensuring symmetry in the infinite planar setting. Regular tessellations of the plane, denoted Schläfli symbol {p,q}\{p, q\} where pp is the number of sides per face and qq the number of faces meeting at each vertex, illustrate this duality clearly. For the square tessellation {4,4}\{4, 4\}, the primal graph is the infinite 4-regular grid Z2\mathbb{Z}^2, and its dual is also {4,4}\{4, 4\}, making it self-dual. In contrast, the triangular {3,6}\{3, 6\} has dual the hexagonal {6,3}\{6, 3\}, where each triangular face corresponds to a hexagonal vertex in the dual, and vice versa; these are interchanged under duality. Such pairs arise because the dual of {p,q}\{p, q\} is {q,p}\{q, p\}, a property holding for Euclidean tessellations where (p−2)(q−2)=4(p-2)(q-2) = 4. For infinite planar graphs embedded as , the dual preserves planarity and local finiteness when the primal is 3-connected with a tame embedding (piecewise linear, no accumulation points). Self-duality in this context occurs when the tessellation is combinatorially isomorphic to its dual via a preserving incidence, and for those with finitely many face orbits under the , such tilings can be realized metrically in the with automorphisms induced by isometries. There are exactly 46 self-dual pairings of Euclidean wallpaper groups enabling harmonious self-duality, where all automorphisms stem from rigid motions interchanging the tiling and its dual. measures, such as the Gauss-Bonnet applied to tessellations, further link duals: the total vertex in GG equals that of the faces in G∗G^*, summing to zero for the .

Non-planar duals

While the classical dual graph is defined for planar embeddings, the notion extends naturally to non-planar graphs via cellular embeddings on surfaces of positive . A cellular embedding of a graph GG on an orientable surface SS of g≥1g \geq 1 is a where every face is homeomorphic to an open disk, ensuring the embedding is 2-cell. The dual graph G∗G^* is then constructed by placing a vertex in each face of the embedding and an edge between two vertices if the corresponding faces share an edge in GG, with the dual edge crossing the primal edge transversely. This construction yields a in general, as multiple edges in GG between the same pair of faces produce parallel edges in G∗G^*. A key property preserved from the planar case is that duality is an involution: the dual of G∗G^* recovers GG, provided the embedding is cellular. The Euler characteristic of the embedding satisfies χ(G)=v−e+f=2−2g\chi(G) = v - e + f = 2 - 2g, where vv, ee, and ff are the numbers of vertices, edges, and faces of GG, respectively; here, ff equals the number of vertices in G∗G^*. This relation bounds the complexity of embeddings, as higher genus allows denser graphs without crossings. For instance, the complete graph K7K_7 admits a cellular embedding on the torus (g=1g=1), yielding a dual with 7 vertices and reflecting the toroidal topology through its cycles. Unlike planar graphs, where 3-connected graphs have unique embeddings up to by Whitney's , non-planar graphs on higher-genus surfaces may admit multiple non-isomorphic cellular embeddings, each producing a distinct dual graph. This multiplicity arises because the of the surface introduces non-contractible cycles that can be routed differently. Consequently, the geometric dual G∗G^* does not always coincide with the algebraic dual defined via the cycle space orthogonal to the bond space of GG, a distinction absent in the planar setting. Algorithms for computing such duals, including shortest non-separating cycles on the surface, run in O(gn+nlog⁡n)O(gn + n \log n) time for graphs with nn vertices. For non-orientable surfaces, such as the projective plane (g=1g=1), the dual construction follows analogously, with Euler characteristic χ=2−g\chi = 2 - g, but embeddings must respect the surface's crosscap structure. These generalized duals facilitate applications in topological graph theory, such as testing embeddability and computing genus, though they complicate uniqueness compared to planar duals. Seminal treatments emphasize that every finite graph embeds cellularly on some surface of sufficient genus, enabling dual definitions universally.

Abstract and matroid duals

In , the concept of an abstract dual extends the notion of a geometric dual beyond specific embeddings in the plane, providing a combinatorial characterization independent of drawings. Formally, a graph FF is an abstract dual of a graph GG if there is a ϵ:E(G)→E(F)\epsilon: E(G) \to E(F) between their edge sets such that a C⊆E(G)C \subseteq E(G) is a cycle in GG if and only if ϵ(C)\epsilon(C) is a bond (minimal cut-set) in FF. Equivalently, the cycle space of GG corresponds to the bond space (cocycle space) of FF under this bijection. This definition captures the duality relation purely through incidence structures, without reference to faces or crossings. Hassler Whitney established a foundational result linking abstract duality to planarity: a finite graph GG admits an abstract dual if and only if GG is planar. If GG is planar, any geometric dual derived from a plane embedding satisfies the abstract dual condition, as cycles in GG correspond to bonds in the dual via the embedding's face boundaries. Conversely, if GG has an abstract dual FF, then GG cannot contain a subdivision of K5K_5 or K3,3K_{3,3}, the forbidden minors for planarity, because such subdivisions lack corresponding bond structures in any potential dual. This equivalence provides a matroid-theoretic criterion for planarity, where the abstract dual encodes the cographic nature of GG's cycle . The abstract dual concept aligns closely with matroid duality in the framework of graphic matroids. The graphic matroid M(G)M(G) of a graph GG has ground set E(G)E(G) and independent sets corresponding to the forests of GG, with circuits being the cycles of GG. The dual matroid M∗(G)M^*(G) has the same ground set, but its circuits are the minimal dependent sets of the , which for graphic matroids are precisely the bonds of GG. In general, M∗(G)M^*(G) may not be graphic (i.e., representable as M(H)M(H) for some graph HH), but proved that M∗(G)M^*(G) is graphic if and only if GG is planar. In this case, the representing graph HH is (isomorphic to) the dual graph of any plane embedding of GG, confirming that abstract and geometric duals coincide for planar graphs. This perspective generalizes duality beyond graphs: for any MM, the dual M∗M^* is defined such that bases of M∗M^* are complements of bases of MM, and the rank function satisfies r∗(X)=∣X∣−r(M)+r(M/(E∖X))r^*(X) = |X| - r(M) + r(M / (E \setminus X)). In the graphic case, the planarity condition via duality highlights why planar graphs are exceptional among all graphs, as their matroids preserve the graphic structure under dualization, enabling applications in optimization and algorithms. Non-planar graphs, like K5K_5, have dual matroids that are not graphic, manifesting as non-representable structures over the cycle-bond incidence.

Applications

Graph algorithms and planarity testing

Dual graphs play a crucial role in algorithms for planar graphs by providing a dual perspective that transforms certain problems in the primal graph into more tractable ones in the dual. For instance, in a plane graph GG, a cycle in GG corresponds to a bond (minimal cut) in the dual graph G∗G^*, where vertices represent faces of GG and edges connect adjacent faces. This duality enables efficient solutions to connectivity and flow problems. A seminal is that the separating two vertices in GG can be reduced to finding the shortest cycle in G∗G^* that separates the corresponding faces adjacent to those vertices. This correspondence has led to optimized algorithms for maximum flow and in planar graphs. In the work of and Shiloach, the maximum flow between a source and sink in a planar network is computed by finding the minimum-cost separating cycle in the dual graph, leveraging shortest path algorithms like Dijkstra's on G∗G^* after constructing the . Subsequent advancements, such as those by Borradaile and Klein, extend this to multiple-source multiple-sink flows by computing non-crossing shortest paths in the dual, achieving O(nlog⁡n)O(n \log n) time for undirected planar graphs with unit capacities. These methods rely on first obtaining a planar of GG, which introduces as a foundational step. Planarity testing determines whether a graph admits a crossing-free in the plane, a prerequisite for constructing its dual. Seminal for this problem focus on building an incrementally while detecting obstructions. The Hopcroft-Tarjan , running in linear time O(n+m)O(n + m), uses a to add paths between biconnected components and tests for planarity by checking if added edges can be embedded without crossings, effectively building the rotation system that defines the . If planar, this allows linear-time construction of the dual graph by identifying face boundaries via the rotation system and adjacency information. More recent linear-time tests, such as the Boyer-Myrvold algorithm, employ a similar DFS-based approach but use conflict graphs to resolve choices, ensuring the output is either a combinatorial or a Kuratowski subgraph certifying non-planarity. Once the is obtained, dual-based algorithms can be applied immediately; for example, the dual's face degrees match the primal's vertex degrees, facilitating problems like face coloring, which is equivalent to vertex coloring the dual via the for planar graphs. These techniques underscore the interplay between and dual graph exploitation in broader graph algorithms, enabling applications in network design and .

Geometry, polyhedra, and computational geometry

In the context of polyhedra, the dual graph of a polyhedral graph—where vertices represent the faces of the polyhedron and edges connect vertices if the corresponding faces share an edge—coincides with the 1-skeleton (vertex-edge graph) of the geometric dual polyhedron. This correspondence arises because the dual polyhedron interchanges the roles of vertices and faces of the original: each vertex of the dual polyhedron corresponds to a face of the primal, and each edge of the dual connects vertices whose primal faces are adjacent. For instance, the dual graph of the cube (with 6 faces and 12 edges) is the 1-skeleton of the octahedron, which has 6 vertices and 12 edges, preserving the total number of edges while swapping vertex and face counts. This duality extends to f-vectors, where the face vector of the dual polyhedron is the reverse of the primal's, as seen in the cube's f-vector (f_0=8 vertices, f_1=12 edges, f_2=6 faces) mirroring the octahedron's (f_0=6, f_1=12, f_2=8). Self-dual polyhedra, such as the tetrahedron, yield self-dual graphs where the structure is isomorphic to its dual, with the complete graph K_4 serving as both the primal skeleton and its dual. This geometric duality facilitates analysis of properties, such as connectivity and embedding, since the dual graph inherits planarity and 3-connectedness from the primal by Steinitz's theorem, ensuring it too realizes a . For convex , the dual graph's embedding on the sphere reflects the primal's face lattice, enabling combinatorial studies of symmetry and enumeration without direct geometric computation. In , dual graphs underpin efficient algorithms for spatial structures and subdivisions. A prominent example is the of a point set P, where the dual graph connects sites whose Voronoi cells share an edge; this graph is precisely the of P when no four points are cocircular, forming a with O(n) edges that maximizes the minimum angle among triangulations. This duality enables nearest-neighbor queries and , as edges exist between sites p_i and p_j if their connecting disk contains no other points, supporting applications in terrain modeling and molecular simulations with linear-time construction via randomized incremental algorithms. Dual graphs also model adjacencies in planar arrangements, such as line or arrangements, where vertices represent cells (regions) and edges link adjacent cells across a . In line arrangements, the dual graph's structure allows traversal for and problems, with spanning trees of degree at most three enabling efficient point location in O(n log n) time. For triangulated polygons, the dual graph is a , facilitating proofs like Fisk's art gallery theorem, which guarantees floor(n/3) vertex guards suffice for visibility by leveraging 3-colorings of the dual's maximal . Additionally, in mesh processing, dual graphs of triangular meshes (3-regular and bridgeless) support stripification via perfect matchings, reducing rendering complexity by grouping triangles into cyclic strips with at most a 3/2 increase in element count. These applications highlight dual graphs' role in transforming geometric problems into graph-theoretic ones, often yielding optimal or near-linear solutions.

Computer science and engineering

In , particularly in the design of very-large-scale integration (VLSI) circuits, dual graphs facilitate efficient floorplanning by representing module adjacencies in planar layouts. A models a of a bounding into non-overlapping rectangular modules, where vertices correspond to circuit clusters and edges to shared boundaries, preserving topological connectivity while optimizing space utilization. This approach addresses challenges in automated layout generation by ensuring sufficient interfaces for signal routing and minimizing unused area in chip designs. Algorithms for constructing rectangular duals from triangulated planar graphs involve augmenting the graph to a 4-connected completion—adding vertices and edges to form a outer face—followed by iterative paths to assign rectangle dimensions, achieving near-linear in practice for graphs with hundreds of vertices. Such methods have demonstrated practical efficiency, reducing floorplan computation from hours to seconds on mid-1980s hardware like the VAX 750. The foundational theory of rectangular dual graphs equates their existence to a in a constructed from the primal's faces and edges, enabling recognition and synthesis in polynomial time. This framework supports hierarchical and slicing floorplans, where submodules are recursively dualized, aiding scalability in complex integrated circuits with thousands of components. Area-efficient realizations of these duals further incorporate constraints like aspect ratios and pin positions, generating layouts that reduce wire lengths by up to 20% compared to naive placements in benchmark circuits. These techniques remain to modern CAD tools for fabrication. In , dual graphs enable the partitioning and interactive visualization of large-scale polygonal , such as those in digital mockups for simulations. The dual graph of a partition has vertices representing sub- or regions and edges linking adjacent partitions, allowing hierarchical traversal for multi-resolution rendering. This structure supports out-of-core processing by loading only relevant sub- into memory, crucial for handling models exceeding sizes in real-time applications like virtual prototyping. Benefits include reduced rendering latency—by factors of 10 or more for terascale datasets—and seamless integration with level-of-detail hierarchies, enhancing user interaction in CAD visualization pipelines. Self-dual graph theory extends to reconfigurable logic design in circuits, where graphs invariant under duality map to networks implementing multiple functions. A self-dual graph allows a single H-shaped complementary structure to realize gates like XOR, NAND, NOR, AND, by adjusting connections, supporting engineering change orders with minimal area overhead—typically 15-20% less than dedicated cells—and lower dynamic power due to balanced pull-up/pull-down paths. This approach streamlines post-silicon modifications in field-programmable gate arrays and application-specific integrated circuits.

Emerging uses in machine learning and data science

Dual graphs, particularly in the context of planar embeddings and line graphs, have found emerging applications in through enhancements to graph neural networks (GNNs). In dual-primal graph convolutional networks (DPGCNs), convolutions alternate between a primal graph and its dual (often the line graph), enabling the simultaneous learning of vertex and edge features for tasks such as node classification and . This approach addresses limitations in standard GNNs by incorporating neighborhood-aware edge representations, achieving superior performance on benchmarks like the Cora (83.3% accuracy) and MovieLens recommendation (RMSE 0.915). Further advancements leverage dual graphs for subgraph isomorphism counting and matching in GNNs, where the edge-to-vertex dual (line graph) establishes a one-to-one correspondence with primal substructures, facilitating asynchronous . Dual neural networks (DMPNNs) use this duality to improve substructure representation, outperforming baselines in isomorphism counting (e.g., RMSE 0.475 on Erdős-Rényi graphs) and node classification (e.g., 16.54 Macro-F1 on ). In , region adjacency graphs (RAGs)—the dual graphs of image segmentations—serve as inputs to GNNs for tasks like semantic segmentation and analysis, where nodes represent regions and edges capture spatial adjacencies to model hierarchical structures. In applications involving spatial networks, dual graphs model road systems by treating segments as nodes in the dual and intersections as hyperedges, enhancing representation learning for traffic prediction and . A dual graph-based approach combines simple graphs and hypergraphs to capture low- and high-order dependencies, improving embedding quality for downstream tasks like travel time estimation. Similarly, in educational , dual graph ensembles—comprising hypergraphs for exercise-concept relations and directed graphs for interaction sequences—enable knowledge tracing models to predict student performance more accurately than single-graph baselines across multiple datasets. These uses highlight dual graphs' role in bridging geometric structure with neural architectures for robust, interpretable learning on complex data.

History

Origins in geometry and polyhedra

The concept of duality in polyhedra traces its origins to , where the five Platonic solids—, , , , and —were recognized as regular polyhedra with faces as congruent regular polygons and equivalent vertices. In Plato's Timaeus (c. 360 BC), these solids were associated with the classical elements (fire, earth, air, water, and the for the cosmos), implicitly highlighting dual pairs such as the and , where the faces of one correspond to the vertices of the other. (c. 417–369 BC) formalized the construction and regularity of the and , establishing them as a dual pair alongside the self-dual . Euclid's Elements (c. 300 BC) rigorously proved that exactly five regular convex exist, providing a foundational geometric framework that later supported duality principles, as dual interchange vertices and faces while preserving the overall combinatorial structure. (c. 287–212 BC) extended this by describing 13 semi-regular (Archimedean) solids, composed of regular polygons with identical vertex configurations; their duals, known as Catalan solids, feature identical faces meeting in identical ways at each vertex and were systematically identified by in 1865. This duality operation, where edges of the original connect corresponding vertices and faces of the dual, emerged as a natural geometric reciprocity, with the dual of a dual returning the original . During the , advanced the study in Harmonices Mundi (1619), cataloging the Archimedean solids and explicitly discussing dual polyhedra, including depictions of pairs like the cube-octahedron and novel forms such as the (dual to the ) and (dual to the ). Kepler's work emphasized the harmonic proportions and spatial interrelations of duals, bridging geometry with cosmology. In the , Leonhard Euler's polyhedral formula V−E+F=2V - E + F = 2 (1752), derived for convex polyhedra, quantified the balance between vertices (VV), edges (EE), and faces (FF), revealing that dual polyhedra satisfy the same relation since vertices and faces are interchanged. The geometric dual of a polyhedron can be constructed via polar reciprocity with respect to a sphere centered at the origin, where each face of the original becomes a vertex of the dual at the pole of the corresponding plane, ensuring edges connect adjacent faces. (1813) connected polyhedral geometry to planar representations through , paving the way for interpreting the 1-skeleton (vertex-edge graph) of a as a dual graph in the combinatorial sense. This laid the groundwork for modern dual graphs, where vertices represent faces of the original and edges represent adjacency, originating directly from the polyhedral dual's structure.

Developments in graph theory and modern extensions

The formal integration of dual graphs into began in the early 1930s with the work of Hassler Whitney, who introduced the concept of a combinatorial dual for , defined abstractly without reference to a specific geometric . In his 1932 , Whitney proved that for a 3-connected , the combinatorial dual is unique up to and equivalent to the geometric dual obtained from any plane , establishing a foundational duality theorem that bridged geometric intuition with algebraic graph properties. This development facilitated characterizations of planarity, building on Kazimierz Kuratowski's 1930 theorem that a graph is planar if and only if it contains no subdivision of K5K_5 or K3,3K_{3,3}, where dual graphs helped analyze forbidden configurations through face structures. In 1937, Klaus Wagner provided a minor-closed characterization of planar graphs, further leveraging duals to study contractions and embeddings, while Saunders MacLane independently offered a cycle space-based criterion that aligned with dual edge incidences. These advances solidified dual graphs as essential tools for proving structural theorems in planar graph theory. Post-World War II developments extended duals to invariants and algorithms. W.T. Tutte's 1947 introduction of what became known as the captured duality symmetries, satisfying TG∗(x,y)=TG(y,x)T_{G^*}(x,y) = T_G(y,x) for a GG and its dual G∗G^*, enabling computations of spanning trees, colorings, and flows across dual pairs. In the 1970s, algorithmic progress included John Hopcroft and Robert Tarjan's linear-time (1974), which implicitly relies on dual graph constructions to detect cycles and separators. The 1976 proof of the four-color theorem by Kenneth Appel and Wolfgang Haken utilized reducibility arguments on triangulations, where dual graphs modeled face adjacencies to discharge configurations. Modern extensions in graph theory have generalized duals beyond plane embeddings, incorporating them into surface topology and minor theory. Gerhard Ringel and J.W. Thomas Youngs' 1968 solution to the Heawood conjecture on for orientable surfaces employed dual embeddings to bound chromatic numbers, influencing subsequent work on . The graph minors project by and Paul Seymour, spanning 1983 to 2004, used duality in torsos and branch decompositions to characterize minor-closed families, proving that every such family is finitely definable and admitting polynomial-time recognition for fixed obstructions. Bojan Mohar and Carsten Thomassen's 2001 monograph further extended dual concepts to graphs on surfaces, exploring self-duality and voltage graphs for . Subsequent work, such as the 2011 refinement of the graph minor structure theorem, has continued to apply dual principles in algorithmic as of 2025.

References

  1. https://mathworld.wolfram.com/DualGraph.html
  2. https://faculty.etsu.edu/gardnerr/5340/notes-Bondy-Murty-GT/Bondy-Murty-GT-10-2.pdf
  3. https://bookofproofs.github.io/branches/graph-theory/dual-planar-graph.html
  4. https://www.sciencedirect.com/topics/mathematics/dual-graph
  5. https://transportgeography.org/contents/methods/graph-theory-definition-properties/dual-graph/
  6. http://jeffe.cs.illinois.edu/teaching/comptop/2017/chapters/02-planar-graphs.pdf
  7. https://koreascience.or.kr/article/JAKO199325748114657.page
  8. https://www.maplesoft.com/support/help/maple/view.aspx?path=GraphTheory/SpecialGraphs/DipoleGraph
  9. https://www.sciencedirect.com/science/article/pii/S0012365X06005279
  10. https://link.springer.com/article/10.1007/s00010-022-00902-5
  11. https://www.math.brown.edu/tbanchof/Beyond3d/chapter5/section03.html
  12. https://www.zib.de/userpage/groetschel/teaching/WS1314/BondyMurtyGTWA.pdf
  13. https://users.wpi.edu/~bservat/self3.pdf
  14. https://core.ac.uk/download/pdf/82535184.pdf
  15. https://diestel-graph-theory.com/basic.pdf
  16. https://www.ams.org/tran/1932-034-02/S0002-9947-1932-1501641-2/S0002-9947-1932-1501641-2.pdf
  17. https://daiwz.net/course/disc_math/2023/Diestel_Graph_Theory.pdf
  18. https://www.sciencedirect.com/science/article/pii/0095895671900220
  19. https://ics.uci.edu/~eppstein/163/lecture10a.pdf
  20. https://pi.math.cornell.edu/~riley/papers/Dual_Trees/Dual_Trees_arxiv.pdf
  21. https://math.stackexchange.com/questions/764566/spanning-trees-in-planar-dual-graph
  22. https://ti.inf.ethz.ch/ew/courses/Geo21/lecture/gca21-2.pdf
  23. https://www.sciencedirect.com/science/article/pii/0012365X73901696
  24. https://www.sciencedirect.com/science/article/pii/S0304397515000304
  25. https://maths.qmul.ac.uk/~arrow/WU.pdf
  26. https://arxiv.org/pdf/2411.04601
  27. https://arxiv.org/pdf/2308.11517
  28. https://arxiv.org/pdf/1904.03881
  29. https://inria.hal.science/inria-00070220v1/document
  30. https://arxiv.org/pdf/1905.01830
  31. https://www.semanticscholar.org/topic/Medial-graph/641536
  32. https://jeffe.cs.illinois.edu/pubs/pdf/tanglex.pdf
  33. https://arxiv.org/pdf/2002.03550
  34. https://www.uni-ulm.de/fileadmin/website_uni_ulm/mawi.inst.081/Henning/Duality.pdf
  35. https://www.sciencedirect.com/science/article/pii/0095895680900830
  36. https://arxiv.org/pdf/1612.08676
  37. https://users.wpi.edu/~bservat/self5.pdf
  38. http://monge.univ-mlv.fr/~colinde/cours/algo-graphs-surfaces.pdf
  39. https://arxiv.org/pdf/1702.05358
  40. https://www.sfu.ca/~mohar/Book.html
  41. https://cs.brown.edu/people/rtamassi/gdhandbook/chapters/planarity.pdf
  42. https://people.inf.ethz.ch/fukudak/lect/pclect/notes2013/ch5-14.pdf
  43. https://faculty.sites.iastate.edu/jia/files/inline-files/20b.%20delaunay%20triangulation.pdf
  44. https://ics.uci.edu/~eppstein/pubs/Epp-WG-09-talk.pdf
  45. https://dl.acm.org/doi/10.1145/800033.800872
  46. https://dl.acm.org/doi/abs/10.1007/BF01840399
  47. https://ieeexplore.ieee.org/document/1604660
  48. https://ieeexplore.ieee.org/document/10335626
  49. https://arxiv.org/abs/2112.08764
  50. https://www.sciencedirect.com/science/article/pii/S1361841524003694
  51. https://arxiv.org/abs/2304.07298
  52. https://dl.acm.org/doi/10.1145/3638350
  53. http://web.iyte.edu.tr/~gokhankiper/POLYHEDRA%20-%20A%20Historical%20Review.pdf
  54. https://ir.library.louisville.edu/context/etd/article/1646/viewcontent/520.pdf
  55. http://pure-oai.bham.ac.uk/ws/files/166356578/carmesinj2022graph.pdf
  56. https://math.uchicago.edu/~may/REU2016/REUPapers/Tamar-Mattis.pdf
  57. https://www.ams.org/books/spec/108/spec108-endmatter.pdf
  58. https://dokumen.pub/graph-theory-in-america-the-first-hundred-years-9780691240657.html
  59. https://collaborate.princeton.edu/en/publications/the-four-colour-theorem/
  60. https://www.cambridge.org/core/services/aop-cambridge-core/content/view/0B544DF28863D3E9A1D0CDE255DFB072/9781139087223c1_p18-33_CBO.pdf/embedding_graphs_on_surfaces.pdf
  61. https://arxiv.org/abs/1105.3549
  62. https://www.press.jhu.edu/books/title/1675/graphs-surfaces
Add your contribution
Related Hubs
Contribute something
User Avatar
No comments yet.