Hubbry Logo
Orbital nodeOrbital nodeMain
Open search
Orbital node
Community hub
Orbital node
logo
8 pages, 0 posts
0 subscribers
Be the first to start a discussion here.
Be the first to start a discussion here.
Orbital node
Orbital node
Orbital node
View on Wikipedia
from Wikipedia
The longitude of the ascending node is one of several orbital elements.
Part of a series on
Astrodynamics
Orbital elements
Types of two-body orbits by
eccentricity
Equations
Gravitational influences
N-body orbits
Preflight engineering
Efficiency measures
Propulsive maneuvers

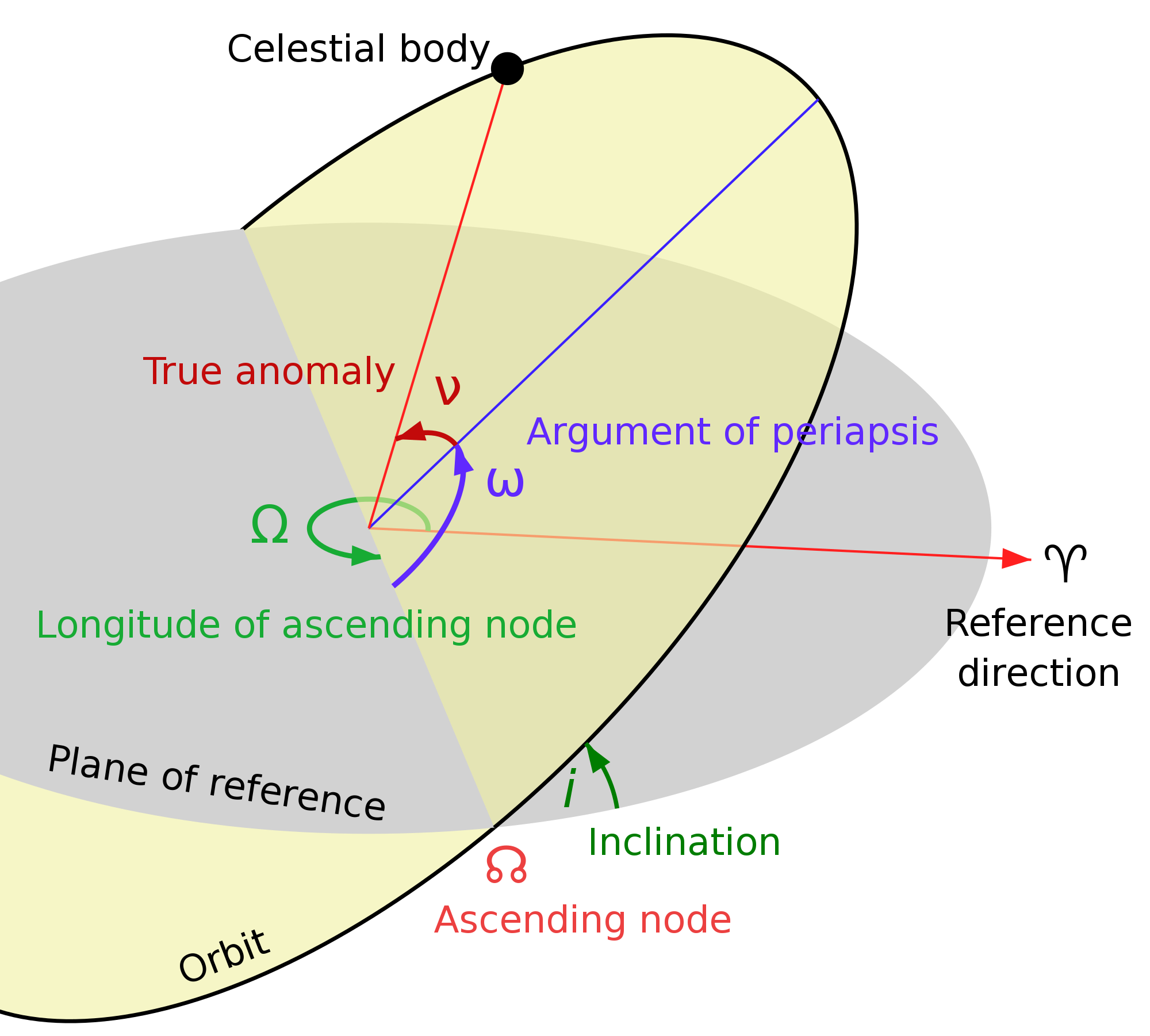
An orbital node is either of the two points where an orbit intersects a plane of reference to which it is inclined.[1] A non-inclined orbit, which is contained in the reference plane, has no nodes.

Planes of reference

[edit]

Common planes of reference include the following:

Node distinction

[edit]
Animation about nodes of two elliptic trajectories. (Click on image.)

If a reference direction from one side of the plane of reference to the other is defined, the two nodes can be distinguished. For geocentric and heliocentric orbits, the ascending node (or north node) is where the orbiting object moves north through the plane of reference, and the descending node (or south node) is where it moves south through the plane.[4] In the case of objects outside the Solar System, the ascending node is the node where the orbiting secondary passes away from the observer, and the descending node is the node where it moves towards the observer.[5], p. 137.

The position of the node may be used as one of a set of parameters, called orbital elements, which describe the orbit. This is done by specifying the longitude of the ascending node (or, sometimes, the longitude of the node).

The line of nodes is the straight line resulting from the intersection of the object's orbital plane with the plane of reference; it passes through the two nodes.[2]

Symbols and nomenclature

[edit]
Look up anabibazon in Wiktionary, the free dictionary.
Look up catabibazon in Wiktionary, the free dictionary.

The symbol of the ascending node is (Unicode: U+260A, ☊), and the symbol of the descending node is (Unicode: U+260B, ☋).

In medieval and early modern times, the ascending and descending nodes of the Moon in the ecliptic plane were called the "dragon's head" (Latin: caput draconis, Arabic: رأس الجوزهر) and "dragon's tail" (Latin: cauda draconis), respectively.[6]: p.141,  [7]: p.245  These terms originally referred to the times when the Moon crossed the apparent path of the sun in the sky (as in a solar eclipse). Also, corruptions of the Arabic term such as ganzaar, genzahar, geuzaar and zeuzahar were used in the medieval West to denote either of the nodes.[8]: pp.196–197,  [9]: p.65,  [10]: pp.95–96 

The Koine Greek terms αναβιβάζων and καταβιβάζων were also used for the ascending and descending nodes, giving rise to the English terms anabibazon and catabibazon.[11][12]:  ¶27 

Lunar nodes

[edit]
Main article: Lunar node
Nodes of the Moon

For the orbit of the Moon around Earth, the plane is taken to be the ecliptic, not the equatorial plane. The gravitational pull of the Sun upon the Moon causes its nodes to gradually precess westward, completing a cycle in approximately 18.6 years.[1][13]

Use in astrology

[edit]

The image of the ascending and descending orbital nodes as the head and tail of a dragon, 180 degrees apart in the sky, goes back to the Chaldeans; it was used by the Zoroastrians, and then by Arabic astronomers and astrologers. In Middle Persian, its head and tail were respectively called gōzihr sar and gōzihr dumb; in Arabic, al-ra's al-jawzihr and al-dhanab al-jawzihr — or in the case of the Moon, ___ al-tennin.[14] Among the arguments against astrologers made by Ibn Qayyim al-Jawziyya (1292–1350), in his Miftah Dar al-SaCadah: "Why is it that you have given an influence to al-Ra's [the head] and al-Dhanab [the tail], which are two imaginary points [ascending and descending nodes]?"[15]

See also

[edit]

References

[edit]
Revisions and contributorsEdit on WikipediaRead on Wikipedia

Orbital node

View on Grokipedia
from Grokipedia
An orbital node is one of the two points where the trajectory of a celestial body, such as a , , or , intersects a specified reference plane to which the is inclined, typically the ecliptic plane for solar system objects or the equatorial plane for Earth-centered orbits. These intersection points define the orientation of the relative to the reference and are fundamental to describing the three-dimensional geometry of orbits in . The two nodes are distinguished by the direction of crossing: the ascending node occurs where the orbiting body passes through the reference plane moving northward (from south to north), while the descending node is where it passes southward (from north to south). The straight line connecting these two points, known as the line of nodes, lies in both the and the reference plane, serving as a key axis for measuring and other parameters. In the context of the six classical Keplerian orbital elements, the —measured as the angle from a fixed reference direction (such as the vernal equinox) to the ascending node along the reference plane—specifies the orbit's rotational orientation around the . This element, denoted by the symbol Ω, is essential for precise and prediction. Orbital nodes play a critical role in various astronomical and practical applications, including spacecraft trajectory planning, where they influence launch windows and orbital insertions to achieve desired inclinations. For natural bodies like the Moon, the nodes relative to the ecliptic determine the timing of solar and lunar eclipses, which occur only when the Sun aligns closely with one of these points during the Moon's orbital cycle. In polar orbits used for Earth observation satellites, nodes ensure systematic coverage as the reference plane (Earth's equator) rotates beneath the orbit.

Fundamentals

Definition

In , the is the geometric plane in which the of a celestial body, such as a or , lies, typically containing the elliptical path around its . An refers to either of the two points where this intersects a chosen reference plane, such as the or equatorial plane, to which the is inclined. These intersections occur twice per orbit for inclined paths, marking the locations where the orbiting body crosses from one side of the reference plane to the other. If the lies entirely within the reference plane, no distinct nodes exist, as the path does not cross it. Nodes are fundamental in describing inclined orbits, as they delineate the transitions across the reference plane and facilitate the parameterization of orbital orientation. The term "node" originates from the Latin word nodus, meaning "knot," reflecting the conceptual or "knotting" of orbital paths with the reference plane, with its astronomical usage emerging in the to denote points of orbital .

Geometry of Nodes

In , the two nodes of an orbit——represent the points where the orbital path intersects the reference plane, such as the equatorial or plane. These nodes lie on the line of nodes, which is the straight-line between the inclined and the reference plane. The line of nodes serves as the axis about which the orbital plane is tilted by the inclination angle ii, and the two nodes are positioned exactly 180 degrees apart along the , ensuring that the trajectory crosses the reference plane symmetrically opposite each other. Visually, the nodes can be illustrated in a of the where the reference plane is depicted as a horizontal line, and the is shown tilted at angle ii. The nodes appear as the intersection points on the elliptical , marking locations where the body's relative to the reference plane—essentially its angular deviation north or south—is precisely zero. At these points, the orbit transitions between the northern and southern hemispheres defined by the reference plane; for instance, the ascending node occurs during the northward crossing. This zero-latitude condition highlights the nodes as the boundaries where the orbit's out-of-plane motion reverses direction. Mathematically, in a aligned with the reference plane (where the -axis is perpendicular to it), the nodes occur at positions where the -coordinate of the orbiting body changes sign, indicating the crossover through the plane. The position vector in this system has a -component given by z=rsin⁡isin⁡(ω+f)z = r \sin i \sin(\omega + f), where rr is the radial distance, ii is the inclination, ω\omega is the argument of periapsis, and ff is the . The nodes satisfy the condition sin⁡isin⁡(ω+f)=0\sin i \sin(\omega + f) = 0; assuming i≠0∘i \neq 0^\circ or 180∘180^\circ, this simplifies to sin⁡(ω+f)=0\sin(\omega + f) = 0, corresponding to ω+f=0∘\omega + f = 0^\circ or 180∘180^\circ ( 360∘360^\circ), which defines the argument of latitude at the nodes. This equation derives from the transformation of into Cartesian coordinates, emphasizing the geometric constraint of planarity at the intersections.

Types and Distinctions

Ascending and Descending Nodes

In , the ascending node is defined as the point along the orbit where the orbiting body intersects the reference plane while moving from the to the , corresponding to an increase in relative to that plane. This crossing occurs in the direction of the body's orbital motion for inclined orbits. Conversely, the descending node is the point where the body crosses the reference plane from the to the , resulting in a decrease in . The descending node is located directly opposite the ascending node along the line of nodes, which forms the intersection between the and the reference plane. For prograde orbits with a positive inclination relative to the reference plane, the ascending node is the first node encountered when traversing the orbit in the direction of motion, as the body rises northward from the plane before reaching the descending node on the return southward. This directional classification is fundamental to describing the orientation and evolution of orbits, such as those of satellites around or planets in the solar system. Although the positions of the ascending and descending nodes are determined by the instantaneous orbital geometry, they are not fixed in inertial space and undergo due to gravitational perturbations, such as those arising from the non-spherical mass distribution of the central body. This precession causes the line of nodes to rotate over time, affecting long-term orbital predictions.

Node Distinction Criteria

The primary criterion for distinguishing between nodes in an is the direction of the body's motion relative to the reference plane's at the crossing point. Specifically, the ascending node is identified as the intersection where the orbiting body crosses the reference plane from south to north (increasing or z-coordinate), while the descending node occurs where it crosses from north to south (decreasing or z-coordinate). This convention ensures unambiguous identification regardless of the orbit's overall orientation, as it focuses on the local velocity component perpendicular to the reference plane. In special cases such as equatorial orbits, where the inclination i=0∘i = 0^\circ or i=180∘i = 180^\circ, the nodes are undefined because the orbital plane coincides with the reference plane, resulting in no distinct crossings. For retrograde orbits with inclination i>90∘i > 90^\circ, the ascending node remains defined by the northward crossing, even though the overall orbital motion is reversed (westward relative to the reference plane's rotation); the distinction relies solely on the local direction of the latitude crossing, not the prograde or retrograde nature of the orbit. Nodes are measured along the orbital path in the direction of motion, with ambiguities resolved using the applied to the vector h=r×v\mathbf{h} = \mathbf{r} \times \mathbf{v}, which defines the orientation of the such that the ascending node corresponds to the positive z-direction crossing. In highly inclined orbits (i>90∘i > 90^\circ), the node labels may appear swapped relative to a fixed inertial frame due to the inverted direction, but they remain consistent with the local crossing convention to maintain uniformity in orbital element definitions.

Reference Planes

Ecliptic Plane

The ecliptic plane is defined as the plane containing around the Sun, serving as the fundamental reference plane for heliocentric orbits throughout the solar system. This plane provides a natural for describing the positions and motions of solar system bodies, as the orbits of most planets lie nearly coplanar with it due to their formation from the same . In , the is used to compute the ascending and descending nodes for bodies with non-zero inclinations, marking the points where their orbits intersect this reference plane. The locations of orbital nodes for solar system planets relative to the determine the geometric conditions for potential alignments, such as planetary transits across the Sun's disk, which occur when an inferior planet passes through its node near the Sun's position. For example, Mercury's has an inclination of about 7° to the , requiring precise nodal alignment for transits to be visible from . Earth's own defines the , resulting in an inclination of 0°, which renders its nodes undefined as there is no with a tilted reference plane. Historically, the properties of the were rigorously quantified by the astronomer around 130 BCE, who accurately measured its inclination to the , known as the obliquity, to within 5 arcminutes of modern values. The current obliquity is approximately 23.44°, reflecting the tilt of 's rotational axis relative to its and influencing seasonal variations on . For minor planets and comets, the nodes relative to the indicate potential crossing points with , which can lead to close approaches or impacts if the body's trajectory aligns such that its perihelion distance allows intersection near 1 AU from the Sun. These crossings are critical for assessing Earth-impact risks, as seen in studies of near-Earth objects where nodal passages at heliocentric distances matching heighten collision probabilities. Representative examples include Earth-crossing asteroids like (29075) 1950 DA, whose moderately inclined orbit facilitates periodic nodal intersections that are monitored for potential hazards.

Equatorial Plane

The equatorial plane serves as a fundamental reference in for Earth-orbiting bodies, defined as the plane perpendicular to the Earth's spin axis and passing through the planet's center, containing the . This plane provides a stable aligned with , with the mean equator preferred for long-term orbital predictions to account for small perturbations and ensure consistency across epochs. In the context of orbital nodes, the equatorial plane is the reference for defining ascending and descending nodes, where an orbit intersects this plane. For geostationary satellites, which operate in equatorial orbits with an inclination of 0°, the orbital plane coincides with the equatorial plane, resulting in no distinct nodes since there are no crossing points. However, during launch planning for such satellites, the projected node positions in the transfer orbit influence launch windows, as the timing must align the launch site's longitude with the desired orbital orientation relative to the reference plane. The orientation of the equatorial plane is not fixed due to and induced by gravitational torques from the and Sun acting on Earth's . These torques cause the plane to wobble, with the dominant nutation period of approximately 18.6 years corresponding to the retrograde of the Moon's orbital nodes, leading to shifts in node positions for satellites over this cycle. Orbital elements, including node longitudes, in Two-Line Element (TLE) sets for satellites are referenced to the True Equator, Mean Equinox (TEME) of date. This convention ensures reliable tracking of near-Earth orbits relative to Earth's rotating frame.

Nomenclature and Calculations

Symbols and Notation

In astronomical literature, the primary symbol for the is the capital Greek letter omega, Ω, denoting the measured eastward from the along the reference plane to the point where the crosses the plane from to north. The line of nodes refers to the straight line passing through the and connecting the nodes, serving as the intersection axis between the and the reference plane. Within the six classical Keplerian orbital elements—which include the semi-major axis a, eccentricity e, inclination i, Ω, ω, and M—the symbol Ω specifically addresses the orientation of the relative to the reference direction. The symbol Ω is the standard notation for the . Orbital nodes lack dedicated symbols in Cartesian coordinate systems, where positions are instead expressed via vector components , and z without explicit nodal references.

Longitude of the Ascending Node

The , denoted by the symbol Ω, is a key orbital element that quantifies the orientation of an orbit's line of nodes relative to a fixed reference direction in the chosen reference plane, such as the or equatorial plane. It represents the , measured eastward in degrees from 0° to 360°, from the vernal equinox (the reference direction) along the reference plane to the ascending node, where the orbiting body crosses the reference plane moving from south to north. This element, alongside the inclination, fully specifies the tilt and rotational position of the . In practice, Ω is computed from the position vector r and velocity vector v of the orbiting body at any epoch. The specific angular momentum vector h is first determined as h = r × v. The node vector n, which points along the line of nodes toward the ascending node, is then derived as n = k × h / |k × h|, where k is the unit vector normal to the reference plane (typically the z-axis). The is obtained using the two-argument arctangent function to preserve quadrant information: Ω=\atantwo(ny,nx)\Omega = \atantwo(n_y, n_x) where nxn_x and nyn_y are the components of n in the reference plane. This method leverages vector cross-products for direct geometric computation without requiring intermediate orbital parameters. Alternatively, the orbital orientation can be transformed using 3-2-1 Euler angle rotations—first by Ω around the z-axis, then by the inclination ii around the new x-axis, and finally by the argument of periapsis ω\omega around the node line—or via equivalent quaternion representations for enhanced numerical stability in simulations. The significance of Ω lies in its role in defining the absolute rotational position of the orbital plane, which influences ground tracks, eclipse seasons, and interplanetary transfer alignments. In the unperturbed , Ω remains constant over time for any . However, gravitational perturbations, particularly from the central body's oblateness captured by the J₂ zonal harmonic, induce , causing Ω to regress (decrease) at a secular rate given approximately by dΩdt≈−32J2(Rep)2ncos⁡i,\frac{d\Omega}{dt} \approx -\frac{3}{2} J_2 \left( \frac{R_e}{p} \right)^2 n \cos i, where J2≈1.0826×10−3J_2 \approx 1.0826 \times 10^{-3} is Earth's second gravitational zonal coefficient, ReR_e is the equatorial radius of the central body (approximately 6378 km for Earth), p=a(1−e2)p = a(1 - e^2) is the semi-latus rectum with semi-major axis aa and eccentricity ee, n=μ/a3n = \sqrt{\mu / a^3}
Add your contribution
Related Hubs
User Avatar
No comments yet.