Recent from talks
Nothing was collected or created yet.
Distributed Bragg reflector
View on Wikipedia

A distributed Bragg reflector (DBR) is a reflector used in waveguides, such as optical fibers. It is a structure formed from multiple layers of alternating materials with different refractive index, or by periodic variation of some characteristic (such as height) of a dielectric waveguide, resulting in periodic variation in the effective refractive index in the guide. Each layer boundary causes a partial reflection and refraction of an optical wave. For waves whose vacuum wavelength is close to four times the optical thickness of the layers, the interaction between these beams generates constructive interference, and the layers act as a high-quality reflector. The range of wavelengths that are reflected is called the photonic stopband. Within this range of wavelengths, light is "forbidden" to propagate in the structure.
Reflectivity
[edit]
The DBR's reflectivity, , for intensity is approximately given by [1]
where and are the respective refractive indices of the originating medium, the two alternating materials, and the terminating medium (i.e. backing or substrate); and is the number of repeated pairs of low/high refractive index material. This formula assumes the repeated pairs all have a quarter-wave thickness (that is , where is the refractive index of the layer, is the thickness of the layer, and is the wavelength of the light).
The frequency bandwidth of the photonic stop-band can be calculated by
where is the central frequency of the band. This configuration gives the largest possible ratio that can be achieved with these two values of the refractive index.[2][3]
Increasing the number of pairs in a DBR increases the mirror reflectivity and increasing the refractive index contrast between the materials in the Bragg pairs increases both the reflectivity and the bandwidth. A common choice of materials for the stack is titanium dioxide (n ≈ 2.5) and silica (n ≈ 1.5).[4] Substituting into the formula above gives a bandwidth of about 200 nm for 630 nm light.
Distributed Bragg reflectors are critical components in vertical cavity surface emitting lasers and other types of narrow-linewidth laser diodes such as distributed feedback (DFB) lasers and distributed bragg reflector (DBR) lasers. They are also used to form the cavity resonator (or optical cavity) in fiber lasers and free electron lasers.
TE and TM mode reflectivity
[edit]
This section discusses the interaction of transverse electric (TE) and transverse magnetic (TM) polarized light with the DBR structure, over several wavelengths and incidence angles. This reflectivity of the DBR structure (described below) was calculated using the transfer-matrix method (TMM), where the TE mode alone is highly reflected by this stack, while the TM modes are passed through. This also shows the DBR acting as a polarizer.
For TE and TM incidence we have the reflection spectra of a DBR stack, corresponding to a 6 layer stack of dielectric contrast of 11.5, between an air and dielectric layers. The thicknesses of the air and dielectric layers are 0.8 and 0.2 of the period, respectively. The wavelength in the figures below, corresponds to multiples of the cell period.
This DBR is also a simple example of a 1D photonic crystal. It has a complete TE band gap, but only a pseudo TM band gap.
Bio-inspired Bragg reflectors
[edit]Bio-inspired Bragg reflectors are 1D photonic crystals inspired by nature. Reflection of light from such a nanostructured matter results in structural colouration. When designed from mesoporous metal-oxides[5][6][7] or polymers,[8] these devices can be used as low-cost vapor/solvents sensors.[9] For example, colour of this porous multi-layered structures will change when the matter filling up the pores is replaced by another, e.g. replacing air with water.
See also
[edit]- Bragg's law – Physical law regarding scattering angles of radiation through a medium
- Bragg diffraction – Physical law regarding scattering angles of radiation through a medium
- Diffraction – Phenomenon of the motion of waves
- Diffraction grating – Optical component which splits light into several beams
- Dielectric mirror – Mirror made of dielectric materials
- Fabry–Pérot interferometer – Optical device with parallel mirrors
- Fiber Bragg grating – Type of distributed Bragg reflector constructed in a short segment of optical fiber
- Photonic-crystal fiber – Class of optical fiber based on the properties of photonic crystals
- Vertical-cavity surface-emitting laser – Type of semiconductor laser diode
- Photonic crystal sensor
References
[edit]- ^ Sheppard, C.J.R. (1995). "Approximate calculation of the reflection coefficient from a stratified medium". Pure and Applied Optics: Journal of the European Optical Society Part A. 4 (5): 665. Bibcode:1995PApOp...4..665S. doi:10.1088/0963-9659/4/5/018.
- ^ Orfanidis, Sophocles J. (2016). Electromagnetic Waves and Antennas. ECE Department, Rutgers University.
- ^ Osting, B. (2012). "Bragg structure and the first spectral gap". Applied Mathematics Letters. 25 (11): 1926–1930. doi:10.1016/j.aml.2012.03.002.
- ^ Paschotta, Rüdiger. "Bragg Mirrors". Encyclopedia of Laser Physics and Technology. RP Photonics. Retrieved May 1, 2009.
- ^ Bertucci, Simone; Megahd, Heba; Dodero, Andrea; Fiorito, Sergio; Di Stasio, Francesco; Patrini, Maddalena; Comoretto, Davide; Lova, Paola (May 4, 2022). "Mild Sol–Gel Conditions and High Dielectric Contrast: A Facile Processing toward Large-Scale Hybrid Photonic Crystals for Sensing and Photocatalysis". ACS Applied Materials & Interfaces. 14 (17): 19806–19817. doi:10.1021/acsami.1c23653. ISSN 1944-8244. PMC 9073830. PMID 35443778.
- ^ Guldin, Stefan; Kolle, Mathias; Stefik, Morgan; Langford, Richard; Eder, Dominik; Wiesner, Ulrich; Steiner, Ullrich (July 6, 2011). "Tunable Mesoporous Bragg Reflectors Based on Block-Copolymer Self-Assembly" (PDF). Advanced Materials. 23 (32): 3664–3668. doi:10.1002/adma.201100640. ISSN 0935-9648. PMID 21732558. S2CID 10065931.
- ^ Ghazzal, Mohamed N.; Deparis, Olivier; De Coninck, Joel; Gaigneaux, Eric M. (2013). "Tailored refractive index of inorganic mesoporous mixed-oxide Bragg stacks with bio-inspired hygrochromic optical properties". Journal of Materials Chemistry C. 1 (39): 6202. doi:10.1039/c3tc31178c. ISSN 2050-7526.
- ^ Lova, Paola; Manfredi, Giovanni; Boarino, Luca; Comite, Antonio; Laus, Michele; Patrini, Maddalena; Marabelli, Franco; Soci, Cesare; Comoretto, Davide (March 10, 2015). "Polymer Distributed Bragg Reflectors for Vapor Sensing". ACS Photonics. 2 (4): 537–543. doi:10.1021/ph500461w. hdl:11696/32604. ISSN 2330-4022.
- ^ Wang, Hui; Zhang, Ke-Qin; Wang, Hui; Zhang, Ke-Qin (March 28, 2013). "Photonic Crystal Structures with Tunable Structure Color as Colorimetric Sensors". Sensors. 13 (4): 4192–4213. doi:10.3390/s130404192. PMC 3673079. PMID 23539027.

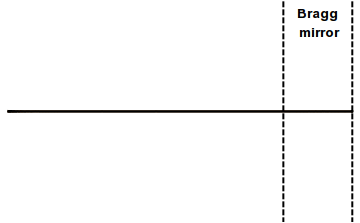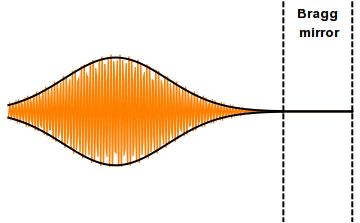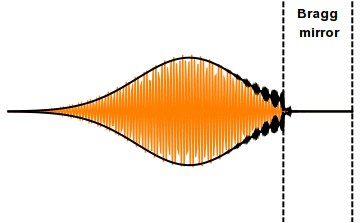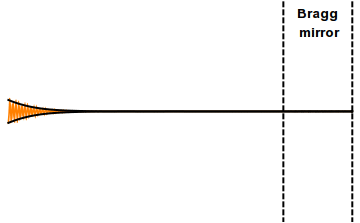

![{\displaystyle R=\left[{\frac {n_{o}(n_{2})^{2N}-n_{s}(n_{1})^{2N}}{n_{o}(n_{2})^{2N}+n_{s}(n_{1})^{2N}}}\right]^{2},}](https://wikimedia.org/api/rest_v1/media/math/render/svg/cd04776409ddec23dff86d2d910739dc6e6839cd)










