Elastic collision

In any collision without an external force, momentum is conserved; but in an elastic collision, kinetic energy is also conserved.^[1] Consider particles A and B with masses m_A, m_B, and velocities v_A1, v_B1 before collision, v_A2, v_B2 after collision. The conservation of momentum before and after the collision is expressed by:^[1] $${\displaystyle m_{A}v_{A1}+m_{B}v_{B1}\ =\ m_{A}v_{A2}+m_{B}v_{B2}.}$$

Likewise, the conservation of the total kinetic energy is expressed by:^[1] $${\displaystyle {\tfrac {1}{2}}m_{A}v_{A1}^{2}+{\tfrac {1}{2}}m_{B}v_{B1}^{2}\ =\ {\tfrac {1}{2}}m_{A}v_{A2}^{2}+{\tfrac {1}{2}}m_{B}v_{B2}^{2}.}$$

These equations may be solved directly to find ${\displaystyle v_{A2},v_{B2}}$ when ${\displaystyle v_{A1},v_{B1}}$ are known:^[2]

$${\displaystyle {\begin{array}{ccc}v_{A2}&=&{\dfrac {m_{A}-m_{B}}{m_{A}+m_{B}}}v_{A1}+{\dfrac {2m_{B}}{m_{A}+m_{B}}}v_{B1}\\[.5em]v_{B2}&=&{\dfrac {2m_{A}}{m_{A}+m_{B}}}v_{A1}+{\dfrac {m_{B}-m_{A}}{m_{A}+m_{B}}}v_{B1}.\end{array}}}$$

Alternatively the final velocity of a particle, v₂ (v_A2 or v_B2) is expressed by:

${\displaystyle v_{2}=(1+e)v_{CoM}-ev_{1}}$

Where:

• e is the coefficient of restitution.
• v_CoM is the velocity of the center of mass of the system of two particles:

${\displaystyle v_{CoM}={\dfrac {m_{A}v_{A1}+m_{B}v_{B1}}{m_{A}+m_{B}}}}$

• v₁ (v_A1 or v_B1) is the initial velocity of the particle.

If both masses are the same, we have a trivial solution: $${\displaystyle {\begin{aligned}v_{A2}&=v_{B1}\\v_{B2}&=v_{A1}.\end{aligned}}}$$ This simply corresponds to the bodies exchanging their initial velocities with each other.^[2]

As can be expected, the solution is invariant under adding a constant to all velocities (Galilean relativity), which is like using a frame of reference with constant translational velocity. Indeed, to derive the equations, one may first change the frame of reference so that one of the known velocities is zero, determine the unknown velocities in the new frame of reference, and convert back to the original frame of reference.

Before collision

Ball A: mass = 3 kg, velocity = 4 m/s

Ball B: mass = 5 kg, velocity = 0 m/s

After collision

Ball A: velocity = −1 m/s

Ball B: velocity = 3 m/s

Another situation:

The following illustrate the case of equal mass, ${\displaystyle m_{A}=m_{B}}$.

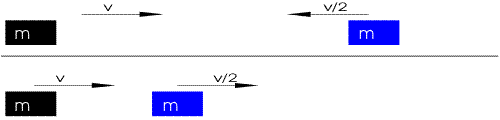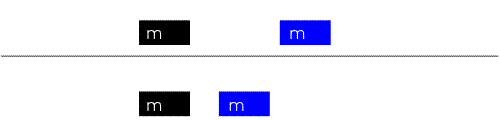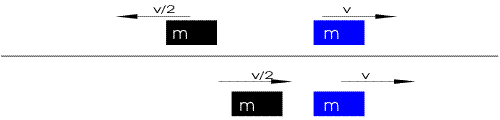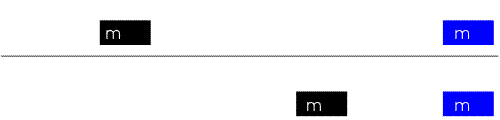
In the limiting case where ${\displaystyle m_{A}}$ is much larger than ${\displaystyle m_{B}}$, such as a ping-pong paddle hitting a ping-pong ball or an SUV hitting a trash can, the heavier mass hardly changes velocity, while the lighter mass bounces off, reversing its velocity plus approximately twice that of the heavy one.^[3]

In the case of a large ${\displaystyle v_{A1}}$, the value of ${\displaystyle v_{A2}}$ is small if the masses are approximately the same: hitting a much lighter particle does not change the velocity much, hitting a much heavier particle causes the fast particle to bounce back with high speed. This is why a neutron moderator (a medium which slows down fast neutrons, thereby turning them into thermal neutrons capable of sustaining a chain reaction) is a material full of atoms with light nuclei which do not easily absorb neutrons: the lightest nuclei have about the same mass as a neutron.

To derive the above equations for ${\displaystyle v_{A2},v_{B2},}$ rearrange the kinetic energy and momentum equations:

$${\displaystyle {\begin{aligned}m_{A}(v_{A2}^{2}-v_{A1}^{2})&=m_{B}(v_{B1}^{2}-v_{B2}^{2})\\m_{A}(v_{A2}-v_{A1})&=m_{B}(v_{B1}-v_{B2})\end{aligned}}}$$

Dividing each side of the top equation by each side of the bottom equation, and using ${\displaystyle {\tfrac {a^{2}-b^{2}}{(a-b)}}=a+b,}$ gives:

$${\displaystyle v_{A2}+v_{A1}=v_{B1}+v_{B2}\quad \Rightarrow \quad v_{A2}-v_{B2}=v_{B1}-v_{A1}}$$

That is, the relative velocity of one particle with respect to the other is reversed by the collision.

Now the above formulas follow from solving a system of linear equations for ${\displaystyle v_{A2},v_{B2},}$; this is done by regarding

${\displaystyle m_{A},m_{B},v_{A1},v_{B1}}$

as constants:

$${\displaystyle \left\{{\begin{array}{rcrcc}v_{A2}&-&v_{B2}&=&v_{B1}-v_{A1}\\m_{A}v_{A1}&+&m_{B}v_{B1}&=&m_{A}v_{A2}+m_{B}v_{B2}.\end{array}}\right.}$$ Once ${\displaystyle v_{A2}}$ is determined, ${\displaystyle v_{B2}}$ can be found by symmetry.

With respect to the center of mass, both velocities are reversed by the collision: a heavy particle moves slowly toward the center of mass, and bounces back with the same low speed, and a light particle moves fast toward the center of mass, and bounces back with the same high speed.

The velocity of the center of mass does not change by the collision. To see this, consider the center of mass at time ${\displaystyle t}$ before collision and time ${\displaystyle t'}$ after collision: $${\displaystyle {\begin{aligned}{\bar {x}}(t)&={\frac {m_{A}x_{A}(t)+m_{B}x_{B}(t)}{m_{A}+m_{B}}}\\{\bar {x}}(t')&={\frac {m_{A}x_{A}(t')+m_{B}x_{B}(t')}{m_{A}+m_{B}}}.\end{aligned}}}$$

Hence, the velocities of the center of mass before and after collision are: $${\displaystyle {\begin{aligned}v_{\bar {x}}&={\frac {m_{A}v_{A1}+m_{B}v_{B1}}{m_{A}+m_{B}}}\\v_{\bar {x}}'&={\frac {m_{A}v_{A2}+m_{B}v_{B2}}{m_{A}+m_{B}}}.\end{aligned}}}$$

The numerators of ${\displaystyle v_{\bar {x}}}$ and ${\displaystyle v_{\bar {x}}'}$ are the total momenta before and after collision. Since momentum is conserved, we have ${\displaystyle v_{\bar {x}}=v_{\bar {x}}'\,.}$

According to special relativity, $${\displaystyle p={\frac {mv}{\sqrt {1-{\frac {v^{2}}{c^{2}}}}}}}$$ where p denotes momentum of any particle with mass m, v denotes velocity, and c is the speed of light.

In the center of momentum frame where the total momentum equals zero, $${\displaystyle {\begin{aligned}p_{1}&=-p_{2}\\p_{1}^{2}&=p_{2}^{2}\\E&={\sqrt {m_{1}^{2}c^{4}+p_{1}^{2}c^{2}}}+{\sqrt {m_{2}^{2}c^{4}+p_{2}^{2}c^{2}}}=E\\p_{1}&=\pm {\frac {\sqrt {E^{4}-2E^{2}m_{1}^{2}c^{4}-2E^{2}m_{2}^{2}c^{4}+m_{1}^{4}c^{8}-2m_{1}^{2}m_{2}^{2}c^{8}+m_{2}^{4}c^{8}}}{2cE}}\\u_{1}&=-v_{1}.\end{aligned}}}$$

Here ${\displaystyle m_{1},m_{2}}$ represent the rest masses of the two colliding bodies, ${\displaystyle u_{1},u_{2}}$ represent their velocities before collision, ${\displaystyle v_{1},v_{2}}$ their velocities after collision, ${\displaystyle p_{1},p_{2}}$ their momenta, ${\displaystyle c}$ is the speed of light in vacuum, and ${\displaystyle E}$ denotes the total energy, the sum of rest masses and kinetic energies of the two bodies.

Since the total energy and momentum of the system are conserved and their rest masses do not change, it is shown that the momentum of the colliding body is decided by the rest masses of the colliding bodies, total energy and the total momentum. Relative to the center of momentum frame, the momentum of each colliding body does not change magnitude after collision, but reverses its direction of movement.

Comparing with classical mechanics, which gives accurate results dealing with macroscopic objects moving much slower than the speed of light, total momentum of the two colliding bodies is frame-dependent. In the center of momentum frame, according to classical mechanics,

$${\displaystyle {\begin{aligned}m_{1}u_{1}+m_{2}u_{2}&=m_{1}v_{1}+m_{2}v_{2}=0\\m_{1}u_{1}^{2}+m_{2}u_{2}^{2}&=m_{1}v_{1}^{2}+m_{2}v_{2}^{2}\\{\frac {(m_{2}u_{2})^{2}}{2m_{1}}}+{\frac {(m_{2}u_{2})^{2}}{2m_{2}}}&={\frac {(m_{2}v_{2})^{2}}{2m_{1}}}+{\frac {(m_{2}v_{2})^{2}}{2m_{2}}}\\(m_{1}+m_{2})(m_{2}u_{2})^{2}&=(m_{1}+m_{2})(m_{2}v_{2})^{2}\\u_{2}&=-v_{2}\\{\frac {(m_{1}u_{1})^{2}}{2m_{1}}}+{\frac {(m_{1}u_{1})^{2}}{2m_{2}}}&={\frac {(m_{1}v_{1})^{2}}{2m_{1}}}+{\frac {(m_{1}v_{1})^{2}}{2m_{2}}}\\(m_{1}+m_{2})(m_{1}u_{1})^{2}&=(m_{1}+m_{2})(m_{1}v_{1})^{2}\\u_{1}&=-v_{1}\,.\end{aligned}}}$$

This agrees with the relativistic calculation ${\displaystyle u_{1}=-v_{1},}$ despite other differences.

One of the postulates in Special Relativity states that the laws of physics, such as conservation of momentum, should be invariant in all inertial frames of reference. In a general inertial frame where the total momentum could be arbitrary,

$${\displaystyle {\begin{aligned}{\frac {m_{1}\;u_{1}}{\sqrt {1-u_{1}^{2}/c^{2}}}}+{\frac {m_{2}\;u_{2}}{\sqrt {1-u_{2}^{2}/c^{2}}}}&={\frac {m_{1}\;v_{1}}{\sqrt {1-v_{1}^{2}/c^{2}}}}+{\frac {m_{2}\;v_{2}}{\sqrt {1-v_{2}^{2}/c^{2}}}}=p_{T}\\{\frac {m_{1}c^{2}}{\sqrt {1-u_{1}^{2}/c^{2}}}}+{\frac {m_{2}c^{2}}{\sqrt {1-u_{2}^{2}/c^{2}}}}&={\frac {m_{1}c^{2}}{\sqrt {1-v_{1}^{2}/c^{2}}}}+{\frac {m_{2}c^{2}}{\sqrt {1-v_{2}^{2}/c^{2}}}}=E\end{aligned}}}$$ We can look at the two moving bodies as one system of which the total momentum is ${\displaystyle p_{T},}$ the total energy is ${\displaystyle E}$ and its velocity ${\displaystyle v_{c}}$ is the velocity of its center of mass. Relative to the center of momentum frame the total momentum equals zero. It can be shown that ${\displaystyle v_{c}}$ is given by: $${\displaystyle v_{c}={\frac {p_{T}c^{2}}{E}}}$$ Now the velocities before the collision in the center of momentum frame ${\displaystyle u_{1}'}$ and ${\displaystyle u_{2}'}$ are: $${\displaystyle {\begin{aligned}u_{1}'&={\frac {u_{1}-v_{c}}{1-{\frac {u_{1}v_{c}}{c^{2}}}}}\\u_{2}'&={\frac {u_{2}-v_{c}}{1-{\frac {u_{2}v_{c}}{c^{2}}}}}\\v_{1}'&=-u_{1}'\\v_{2}'&=-u_{2}'\\v_{1}&={\frac {v_{1}'+v_{c}}{1+{\frac {v_{1}'v_{c}}{c^{2}}}}}\\v_{2}&={\frac {v_{2}'+v_{c}}{1+{\frac {v_{2}'v_{c}}{c^{2}}}}}\end{aligned}}}$$

When ${\displaystyle u_{1}\ll c}$ and ${\displaystyle u_{2}\ll c\,,}$ $${\displaystyle {\begin{aligned}p_{T}&\approx m_{1}u_{1}+m_{2}u_{2}\\v_{c}&\approx {\frac {m_{1}u_{1}+m_{2}u_{2}}{m_{1}+m_{2}}}\\u_{1}'&\approx u_{1}-v_{c}\approx {\frac {m_{1}u_{1}+m_{2}u_{1}-m_{1}u_{1}-m_{2}u_{2}}{m_{1}+m_{2}}}={\frac {m_{2}(u_{1}-u_{2})}{m_{1}+m_{2}}}\\u_{2}'&\approx {\frac {m_{1}(u_{2}-u_{1})}{m_{1}+m_{2}}}\\v_{1}'&\approx {\frac {m_{2}(u_{2}-u_{1})}{m_{1}+m_{2}}}\\v_{2}'&\approx {\frac {m_{1}(u_{1}-u_{2})}{m_{1}+m_{2}}}\\v_{1}&\approx v_{1}'+v_{c}\approx {\frac {m_{2}u_{2}-m_{2}u_{1}+m_{1}u_{1}+m_{2}u_{2}}{m_{1}+m_{2}}}={\frac {u_{1}(m_{1}-m_{2})+2m_{2}u_{2}}{m_{1}+m_{2}}}\\v_{2}&\approx {\frac {u_{2}(m_{2}-m_{1})+2m_{1}u_{1}}{m_{1}+m_{2}}}\end{aligned}}}$$

Therefore, the classical calculation holds true when the speed of both colliding bodies is much lower than the speed of light (~300,000 kilometres per second).

Using the so-called parameter of velocity ${\displaystyle s}$ (usually called the rapidity),

$${\displaystyle {\frac {v}{c}}=\tanh(s),}$$ we get $${\displaystyle {\sqrt {1-{\frac {v^{2}}{c^{2}}}}}=\operatorname {sech} (s).}$$

Relativistic energy and momentum are expressed as follows: $${\displaystyle {\begin{aligned}E&={\frac {mc^{2}}{\sqrt {1-{\frac {v^{2}}{c^{2}}}}}}=mc^{2}\cosh(s)\\p&={\frac {mv}{\sqrt {1-{\frac {v^{2}}{c^{2}}}}}}=mc\sinh(s)\end{aligned}}}$$

Equations sum of energy and momentum colliding masses ${\displaystyle m_{1}}$ and ${\displaystyle m_{2},}$ (velocities ${\displaystyle v_{1},v_{2},u_{1},u_{2}}$ correspond to the velocity parameters ${\displaystyle s_{1},s_{2},s_{3},s_{4}}$), after dividing by adequate power ${\displaystyle c}$ are as follows: $${\displaystyle {\begin{aligned}m_{1}\cosh(s_{1})+m_{2}\cosh(s_{2})&=m_{1}\cosh(s_{3})+m_{2}\cosh(s_{4})\\m_{1}\sinh(s_{1})+m_{2}\sinh(s_{2})&=m_{1}\sinh(s_{3})+m_{2}\sinh(s_{4})\end{aligned}}}$$

and dependent equation, the sum of above equations: $${\displaystyle m_{1}e^{s_{1}}+m_{2}e^{s_{2}}=m_{1}e^{s_{3}}+m_{2}e^{s_{4}}}$$

subtract squares both sides equations "momentum" from "energy" and use the identity ${\textstyle \cosh ^{2}(s)-\sinh ^{2}(s)=1,}$ after simplifying we get: $${\displaystyle 2m_{1}m_{2}(\cosh(s_{1})\cosh(s_{2})-\sinh(s_{2})\sinh(s_{1}))=2m_{1}m_{2}(\cosh(s_{3})\cosh(s_{4})-\sinh(s_{4})\sinh(s_{3}))}$$

for non-zero mass, using the hyperbolic trigonometric identity ${\textstyle \cosh(a-b)=\cosh(a)\cosh(b)-\sinh(b)\sinh(a),}$ we get: $${\displaystyle \cosh(s_{1}-s_{2})=\cosh(s_{3}-s_{4})}$$

as functions ${\displaystyle \cosh(s)}$ is even we get two solutions: $${\displaystyle {\begin{aligned}s_{1}-s_{2}&=s_{3}-s_{4}\\s_{1}-s_{2}&=-s_{3}+s_{4}\end{aligned}}}$$ from the last equation, leading to a non-trivial solution, we solve ${\displaystyle s_{2}}$ and substitute into the dependent equation, we obtain ${\displaystyle e^{s_{1}}}$ and then ${\displaystyle e^{s_{2}},}$ we have: $${\displaystyle {\begin{aligned}e^{s_{1}}&=e^{s_{4}}{\frac {m_{1}e^{s_{3}}+m_{2}e^{s_{4}}}{m_{1}e^{s_{4}}+m_{2}e^{s_{3}}}}\\e^{s_{2}}&=e^{s_{3}}{\frac {m_{1}e^{s_{3}}+m_{2}e^{s_{4}}}{m_{1}e^{s_{4}}+m_{2}e^{s_{3}}}}\end{aligned}}}$$

It is a solution to the problem, but expressed by the parameters of velocity. Return substitution to get the solution for velocities is: $${\displaystyle {\begin{aligned}v_{1}/c&=\tanh(s_{1})={\frac {e^{s_{1}}-e^{-s_{1}}}{e^{s_{1}}+e^{-s_{1}}}}\\v_{2}/c&=\tanh(s_{2})={\frac {e^{s_{2}}-e^{-s_{2}}}{e^{s_{2}}+e^{-s_{2}}}}\end{aligned}}}$$

Substitute the previous solutions and replace: ${\displaystyle e^{s_{3}}={\sqrt {\frac {c+u_{1}}{c-u_{1}}}}}$ and ${\displaystyle e^{s_{4}}={\sqrt {\frac {c+u_{2}}{c-u_{2}}}},}$ after long transformation, with substituting: ${\textstyle Z={\sqrt {\left(1-u_{1}^{2}/c^{2}\right)\left(1-u_{2}^{2}/c^{2}\right)}}}$ we get: $${\displaystyle {\begin{aligned}v_{1}&={\frac {2m_{1}m_{2}c^{2}u_{2}Z+2m_{2}^{2}c^{2}u_{2}-(m_{1}^{2}+m_{2}^{2})u_{1}u_{2}^{2}+(m_{1}^{2}-m_{2}^{2})c^{2}u_{1}}{2m_{1}m_{2}c^{2}Z-2m_{2}^{2}u_{1}u_{2}-(m_{1}^{2}-m_{2}^{2})u_{2}^{2}+(m_{1}^{2}+m_{2}^{2})c^{2}}}\\v_{2}&={\frac {2m_{1}m_{2}c^{2}u_{1}Z+2m_{1}^{2}c^{2}u_{1}-(m_{1}^{2}+m_{2}^{2})u_{1}^{2}u_{2}+(m_{2}^{2}-m_{1}^{2})c^{2}u_{2}}{2m_{1}m_{2}c^{2}Z-2m_{1}^{2}u_{1}u_{2}-(m_{2}^{2}-m_{1}^{2})u_{1}^{2}+(m_{1}^{2}+m_{2}^{2})c^{2}}}\,.\end{aligned}}}$$

For the case of two non-spinning colliding bodies in two dimensions, the motion of the bodies is determined by the three conservation laws of momentum, kinetic energy and angular momentum. The overall velocity of each body must be split into two perpendicular velocities: one tangent to the common normal surfaces of the colliding bodies at the point of contact, the other along the line of collision. Since the collision only imparts force along the line of collision, the velocities that are tangent to the point of collision do not change. The velocities along the line of collision can then be used in the same equations as a one-dimensional collision. The final velocities can then be calculated from the two new component velocities and will depend on the point of collision. Studies of two-dimensional collisions are conducted for many bodies in the framework of a two-dimensional gas.

In a center of momentum frame at any time the velocities of the two bodies are in opposite directions, with magnitudes inversely proportional to the masses. In an elastic collision these magnitudes do not change. The directions may change depending on the shapes of the bodies and the point of impact. For example, in the case of spheres the angle depends on the distance between the (parallel) paths of the centers of the two bodies. Any non-zero change of direction is possible: if this distance is zero the velocities are reversed in the collision; if it is close to the sum of the radii of the spheres the two bodies are only slightly deflected.

Assuming that the second particle is at rest before the collision, the angles of deflection of the two particles, ${\displaystyle \theta _{1}}$ and ${\displaystyle \theta _{2}}$, are related to the angle of deflection ${\displaystyle \theta }$ in the system of the center of mass by^[4] $${\displaystyle \tan \theta _{1}={\frac {m_{2}\sin \theta }{m_{1}+m_{2}\cos \theta }},\qquad \theta _{2}={\frac {{\pi }-{\theta }}{2}}.}$$ The magnitudes of the velocities of the particles after the collision are: $${\displaystyle {\begin{aligned}v'_{1}&=v_{1}{\frac {\sqrt {m_{1}^{2}+m_{2}^{2}+2m_{1}m_{2}\cos \theta }}{m_{1}+m_{2}}}\\v'_{2}&=v_{1}{\frac {2m_{1}}{m_{1}+m_{2}}}\sin {\frac {\theta }{2}}.\end{aligned}}}$$

The final x and y velocities components of the first ball can be calculated as:^[5] $${\displaystyle {\begin{aligned}v'_{1x}&={\frac {v_{1}\cos(\theta _{1}-\varphi )(m_{1}-m_{2})+2m_{2}v_{2}\cos(\theta _{2}-\varphi )}{m_{1}+m_{2}}}\cos(\varphi )+v_{1}\sin(\theta _{1}-\varphi )\cos(\varphi +{\tfrac {\pi }{2}})\\[0.8em]v'_{1y}&={\frac {v_{1}\cos(\theta _{1}-\varphi )(m_{1}-m_{2})+2m_{2}v_{2}\cos(\theta _{2}-\varphi )}{m_{1}+m_{2}}}\sin(\varphi )+v_{1}\sin(\theta _{1}-\varphi )\sin(\varphi +{\tfrac {\pi }{2}}),\end{aligned}}}$$ where v₁ and v₂ are the scalar sizes of the two original speeds of the objects, m₁ and m₂ are their masses, θ₁ and θ₂ are their movement angles, that is, ${\displaystyle v_{1x}=v_{1}\cos \theta _{1},\;v_{1y}=v_{1}\sin \theta _{1}}$ (meaning moving directly down to the right is either a −45° angle, or a 315° angle), and lowercase phi (φ) is the contact angle. (To get the x and y velocities of the second ball, one needs to swap all the '1' subscripts with '2' subscripts.)

This equation is derived from the fact that the interaction between the two bodies is easily calculated along the contact angle, meaning the velocities of the objects can be calculated in one dimension by rotating the x and y axis to be parallel with the contact angle of the objects, and then rotated back to the original orientation to get the true x and y components of the velocities.^{[6][7][8][9][10][11]}

In an angle-free representation, the changed velocities are computed using the centers x₁ and x₂ at the time of contact as

$${\displaystyle {\begin{aligned}\mathbf {v} '_{1}&=\mathbf {v} _{1}-{\frac {2m_{2}}{m_{1}+m_{2}}}\ {\frac {\langle \mathbf {v} _{1}-\mathbf {v} _{2},\,\mathbf {x} _{1}-\mathbf {x} _{2}\rangle }{\|\mathbf {x} _{1}-\mathbf {x} _{2}\|^{2}}}\ (\mathbf {x} _{1}-\mathbf {x} _{2}),\\\mathbf {v} '_{2}&=\mathbf {v} _{2}-{\frac {2m_{1}}{m_{1}+m_{2}}}\ {\frac {\langle \mathbf {v} _{2}-\mathbf {v} _{1},\,\mathbf {x} _{2}-\mathbf {x} _{1}\rangle }{\|\mathbf {x} _{2}-\mathbf {x} _{1}\|^{2}}}\ (\mathbf {x} _{2}-\mathbf {x} _{1})\end{aligned}}}$$

1

where the angle brackets indicate the inner product (or dot product) of two vectors.

In the particular case of particles having equal masses, it can be verified by direct computation from the result above that the scalar product of the velocities before and after the collision are the same, that is ${\displaystyle \langle \mathbf {v} '_{1},\mathbf {v} '_{2}\rangle =\langle \mathbf {v} _{1},\mathbf {v} _{2}\rangle .}$ Although this product is not an additive invariant in the same way that momentum and kinetic energy are for elastic collisions, it seems that preservation of this quantity can nonetheless be used to derive higher-order conservation laws.^[12]

The impulse ${\displaystyle \mathbf {J} }$ during the collision for each particle is:

$${\displaystyle {\begin{aligned}\mathbf {p'_{1}} -\mathbf {p_{1}} &=\mathbf {J_{1}} ,\\\mathbf {p'_{2}} -\mathbf {p_{2}} &=\mathbf {J_{2}} \end{aligned}}}$$

2

Conservation of Momentum implies ${\displaystyle \mathbf {J} \equiv \mathbf {J_{1}} =-\mathbf {J_{2}} }$ .

Since the force during collision is perpendicular to both particles' surfaces at the contact point, the impulse is along the line parallel to ${\displaystyle \mathbf {x} _{1}-\mathbf {x} _{2}\equiv \Delta \mathbf {x} }$, the relative vector between the particles' center at collision time:

${\displaystyle \mathbf {J} =\lambda \,\mathbf {\hat {n}} ,}$ for some ${\displaystyle \lambda }$ to be determined and ${\displaystyle \mathbf {\hat {n}} \equiv {\frac {\Delta \mathbf {x} }{\|\Delta \mathbf {x} \|}}}$

Then from (2):

$${\displaystyle {\begin{aligned}\mathbf {v'_{1}} &=\mathbf {v_{1}} +{\frac {\lambda }{m_{1}}}\mathbf {\hat {n}} ,\\\mathbf {v'_{2}} &=\mathbf {v_{2}} -{\frac {\lambda }{m_{2}}}\mathbf {\hat {n}} \end{aligned}}}$$

3

From above equations, conservation of kinetic energy now requires:

${\displaystyle \lambda ^{2}{\frac {m_{1}+m_{2}}{m_{1}m_{2}}}+2\lambda \,\langle \mathbf {\hat {n}} ,\Delta \mathbf {v} \rangle =0,\quad }$with ${\displaystyle \quad \Delta \mathbf {v} \equiv \mathbf {v} _{1}-\mathbf {v} _{2}.}$

The both solutions of this equation are ${\displaystyle \lambda =0}$ and ${\displaystyle \lambda =-2{\frac {m_{1}m_{2}}{m_{1}+m_{2}}}\langle \mathbf {\hat {n}} ,\Delta \mathbf {v} \rangle }$, where ${\displaystyle \lambda =0}$ corresponds to the trivial case of no collision. Substituting the non trivial value of ${\displaystyle \lambda }$ in (3) we get the desired result (1).

Since all equations are in vectorial form, this derivation is valid also for three dimensions with spheres.

• Collision
• Inelastic collision
• Coefficient of restitution