Hubbry Logo
Homology modelingHomology modelingMain
Open search
Homology modeling
Community hub
Homology modeling
logo
8 pages, 0 posts
0 subscribers
Be the first to start a discussion here.
Be the first to start a discussion here.
Homology modeling
Homology modeling
Homology modeling
View on Wikipedia
from Wikipedia
Homology model of the DHRS7B protein created with Swiss-model and rendered with PyMOL

Homology modeling, also known as comparative modeling of protein, refers to constructing an atomic-resolution model of the "target" protein from its amino acid sequence and an experimental three-dimensional structure of a related homologous protein (the "template"). Homology modeling relies on the identification of one or more known protein structures likely to resemble the structure of the query sequence, and on the production of a sequence alignment that maps residues in the query sequence to residues in the template sequence. It has been seen that protein structures are more conserved than protein sequences amongst homologues, but sequences falling below a 20% sequence identity can have very different structure.[1]

Evolutionarily related proteins have similar sequences and naturally occurring homologous proteins have similar protein structure. It has been shown that three-dimensional protein structure is evolutionarily more conserved than would be expected on the basis of sequence conservation alone.[2]

The sequence alignment and template structure are then used to produce a structural model of the target. Because protein structures are more conserved than DNA sequences, and detectable levels of sequence similarity usually imply significant structural similarity.[3]

The quality of the homology model is dependent on the quality of the sequence alignment and template structure. The approach can be complicated by the presence of alignment gaps (commonly called indels) that indicate a structural region present in the target but not in the template, and by structure gaps in the template that arise from poor resolution in the experimental procedure (usually X-ray crystallography) used to solve the structure. Model quality declines with decreasing sequence identity; a typical model has ~1–2 Å root mean square deviation between the matched Cα atoms at 70% sequence identity but only 2–4 Å agreement at 25% sequence identity. However, the errors are significantly higher in the loop regions, where the amino acid sequences of the target and template proteins may be completely different.

Regions of the model that were constructed without a template, usually by loop modeling, are generally much less accurate than the rest of the model. Errors in side chain packing and position also increase with decreasing identity, and variations in these packing configurations have been suggested as a major reason for poor model quality at low identity.[4] Taken together, these various atomic-position errors are significant and impede the use of homology models for purposes that require atomic-resolution data, such as drug design and protein–protein interaction predictions; even the quaternary structure of a protein may be difficult to predict from homology models of its subunit(s). Nevertheless, homology models can be useful in reaching qualitative conclusions about the biochemistry of the query sequence, especially in formulating hypotheses about why certain residues are conserved, which may in turn lead to experiments to test those hypotheses. For example, the spatial arrangement of conserved residues may suggest whether a particular residue is conserved to stabilize the folding, to participate in binding some small molecule, or to foster association with another protein or nucleic acid.[5]

Homology modeling can produce high-quality structural models when the target and template are closely related, which has inspired the formation of a structural genomics consortium dedicated to the production of representative experimental structures for all classes of protein folds.[6] The chief inaccuracies in homology modeling, which worsen with lower sequence identity, derive from errors in the initial sequence alignment and from improper template selection.[7] Like other methods of structure prediction, current practice in homology modeling is assessed in a biennial large-scale experiment known as the Critical Assessment of Techniques for Protein Structure Prediction, or Critical Assessment of Structure Prediction (CASP).

Motive

[edit]

The method of homology modeling is based on the observation that protein tertiary structure is better conserved than amino acid sequence.[3] Thus, even proteins that have diverged appreciably in sequence but still share detectable similarity will also share common structural properties, particularly the overall fold. Because it is difficult and time-consuming to obtain experimental structures from methods such as X-ray crystallography and protein NMR for every protein of interest, homology modeling can provide useful structural models for generating hypotheses about a protein's function and directing further experimental work.

There are exceptions to the general rule that proteins sharing significant sequence identity will share a fold. For example, a judiciously chosen set of mutations of less than 50% of a protein can cause the protein to adopt a completely different fold.[8][9] However, such a massive structural rearrangement is unlikely to occur in evolution, especially since the protein is usually under the constraint that it must fold properly and carry out its function in the cell. Consequently, the roughly folded structure of a protein (its "topology") is conserved longer than its amino-acid sequence and much longer than the corresponding DNA sequence; in other words, two proteins may share a similar fold even if their evolutionary relationship is so distant that it cannot be discerned reliably. For comparison, the function of a protein is conserved much less than the protein sequence, since relatively few changes in amino-acid sequence are required to take on a related function.

Steps in model production

[edit]

The homology modeling procedure can be broken down into four sequential steps: template selection, target-template alignment, model construction, and model assessment.[3] The first two steps are often essentially performed together, as the most common methods of identifying templates rely on the production of sequence alignments; however, these alignments may not be of sufficient quality because database search techniques prioritize speed over alignment quality. These processes can be performed iteratively to improve the quality of the final model, although quality assessments that are not dependent on the true target structure are still under development.

Optimizing the speed and accuracy of these steps for use in large-scale automated structure prediction is a key component of structural genomics initiatives, partly because the resulting volume of data will be too large to process manually and partly because the goal of structural genomics requires providing models of reasonable quality to researchers who are not themselves structure prediction experts.[3]

Template selection and sequence alignment

[edit]

The critical first step in homology modeling is the identification of the best template structure, if indeed any are available. The simplest method of template identification relies on serial pairwise sequence alignments aided by database search techniques such as FASTA and BLAST. More sensitive methods based on multiple sequence alignment – of which PSI-BLAST is the most common example – iteratively update their position-specific scoring matrix to successively identify more distantly related homologs. This family of methods has been shown to produce a larger number of potential templates and to identify better templates for sequences that have only distant relationships to any solved structure. Protein threading,[10] also known as fold recognition or 3D-1D alignment, can also be used as a search technique for identifying templates to be used in traditional homology modeling methods.[3] Recent CASP experiments indicate that some protein threading methods such as RaptorX are more sensitive than purely sequence(profile)-based methods when only distantly-related templates are available for the proteins under prediction. When performing a BLAST search, a reliable first approach is to identify hits with a sufficiently low E-value, which are considered sufficiently close in evolution to make a reliable homology model. Other factors may tip the balance in marginal cases; for example, the template may have a function similar to that of the query sequence, or it may belong to a homologous operon. However, a template with a poor E-value should generally not be chosen, even if it is the only one available, since it may well have a wrong structure, leading to the production of a misguided model. A better approach is to submit the primary sequence to fold-recognition servers[10] or, better still, consensus meta-servers which improve upon individual fold-recognition servers by identifying similarities (consensus) among independent predictions.

Often several candidate template structures are identified by these approaches. Although some methods can generate hybrid models with better accuracy from multiple templates,[10][11] most methods rely on a single template. Therefore, choosing the best template from among the candidates is a key step, and can affect the final accuracy of the structure significantly. This choice is guided by several factors, such as the similarity of the query and template sequences, of their functions, and of the predicted query and observed template secondary structures. Perhaps most importantly, the coverage of the aligned regions: the fraction of the query sequence structure that can be predicted from the template, and the plausibility of the resulting model. Thus, sometimes several homology models are produced for a single query sequence, with the most likely candidate chosen only in the final step.

It is possible to use the sequence alignment generated by the database search technique as the basis for the subsequent model production; however, more sophisticated approaches have also been explored. One proposal generates an ensemble of stochastically defined pairwise alignments between the target sequence and a single identified template as a means of exploring "alignment space" in regions of sequence with low local similarity.[12] "Profile-profile" alignments that first generate a sequence profile of the target and systematically compare it to the sequence profiles of solved structures; the coarse-graining inherent in the profile construction is thought to reduce noise introduced by sequence drift in nonessential regions of the sequence.[13]

Model generation

[edit]

Given a template and an alignment, the information contained therein must be used to generate a three-dimensional structural model of the target, represented as a set of Cartesian coordinates for each atom in the protein. Three major classes of model generation methods have been proposed.[14][15]

Fragment assembly

[edit]

The original method of homology modeling relied on the assembly of a complete model from conserved structural fragments identified in closely related solved structures. For example, a modeling study of serine proteases in mammals identified a sharp distinction between "core" structural regions conserved in all experimental structures in the class, and variable regions typically located in the loops where the majority of the sequence differences were localized. Thus unsolved proteins could be modeled by first constructing the conserved core and then substituting variable regions from other proteins in the set of solved structures.[16] Current implementations of this method differ mainly in the way they deal with regions that are not conserved or that lack a template.[17] The variable regions are often constructed with the help of a protein fragment library.

Segment matching

[edit]

The segment-matching method divides the target into a series of short segments, each of which is matched to its own template fitted from the Protein Data Bank. Thus, sequence alignment is done over segments rather than over the entire protein. Selection of the template for each segment is based on sequence similarity, comparisons of alpha carbon coordinates, and predicted steric conflicts arising from the van der Waals radii of the divergent atoms between target and template.[18]

Satisfaction of spatial restraints

[edit]

The most common current homology modeling method takes its inspiration from calculations required to construct a three-dimensional structure from data generated by NMR spectroscopy. One or more target-template alignments are used to construct a set of geometrical criteria that are then converted to probability density functions for each restraint. Restraints applied to the main protein internal coordinates – protein backbone distances and dihedral angles – serve as the basis for a global optimization procedure that originally used conjugate gradient energy minimization to iteratively refine the positions of all heavy atoms in the protein.[19]

This method had been dramatically expanded to apply specifically to loop modeling, which can be extremely difficult due to the high flexibility of loops in proteins in aqueous solution.[20] A more recent expansion applies the spatial-restraint model to electron density maps derived from cryoelectron microscopy studies, which provide low-resolution information that is not usually itself sufficient to generate atomic-resolution structural models.[21] To address the problem of inaccuracies in initial target-template sequence alignment, an iterative procedure has also been introduced to refine the alignment on the basis of the initial structural fit.[22] The most commonly used software in spatial restraint-based modeling is MODELLER and a database called ModBase has been established for reliable models generated with it.[23]

Loop modeling

[edit]

Regions of the target sequence that are not aligned to a template are modeled by loop modeling; they are the most susceptible to major modeling errors and occur with higher frequency when the target and template have low sequence identity. The coordinates of unmatched sections determined by loop modeling programs are generally much less accurate than those obtained from simply copying the coordinates of a known structure, particularly if the loop is longer than 10 residues. The first two sidechain dihedral angles (χ1 and χ2) can usually be estimated within 30° for an accurate backbone structure; however, the later dihedral angles found in longer side chains such as lysine and arginine are notoriously difficult to predict. Moreover, small errors in χ1 (and, to a lesser extent, in χ2) can cause relatively large errors in the positions of the atoms at the terminus of side chain; such atoms often have a functional importance, particularly when located near the active site.

Model assessment

[edit]

A large number of methods have been developed for selecting a native-like structure from a set of models. Scoring functions have been based on both molecular mechanics energy functions (Lazaridis and Karplus 1999; Petrey and Honig 2000; Feig and Brooks 2002; Felts et al. 2002; Lee and Duan 2004), statistical potentials (Sippl 1995; Melo and Feytmans 1998; Samudrala and Moult 1998; Rojnuckarin and Subramaniam 1999; Lu and Skolnick 2001; Wallqvist et al. 2002; Zhou and Zhou 2002), residue environments (Luthy et al. 1992; Eisenberg et al. 1997; Park et al. 1997; Summa et al. 2005), local side-chain and backbone interactions (Fang and Shortle 2005), orientation-dependent properties (Buchete et al. 2004a,b; Hamelryck 2005), packing estimates (Berglund et al. 2004), solvation energy (Petrey and Honig 2000; McConkey et al. 2003; Wallner and Elofsson 2003; Berglund et al. 2004), hydrogen bonding (Kortemme et al. 2003), and geometric properties (Colovos and Yeates 1993; Kleywegt 2000; Lovell et al. 2003; Mihalek et al. 2003). A number of methods combine different potentials into a global score, usually using a linear combination of terms (Kortemme et al. 2003; Tosatto 2005), or with the help of machine learning techniques, such as neural networks (Wallner and Elofsson 2003) and support vector machines (SVM) (Eramian et al. 2006). Comparisons of different global model quality assessment programs can be found in recent papers by Pettitt et al. (2005), Tosatto (2005), and Eramian et al. (2006).

Less work has been reported on the local quality assessment of models. Local scores are important in the context of modeling because they can give an estimate of the reliability of different regions of a predicted structure. This information can be used in turn to determine which regions should be refined, which should be considered for modeling by multiple templates, and which should be predicted ab initio. Information on local model quality could also be used to reduce the combinatorial problem when considering alternative alignments; for example, by scoring different local models separately, fewer models would have to be built (assuming that the interactions between the separate regions are negligible or can be estimated separately).

One of the most widely used local scoring methods is Verify3D (Luthy et al. 1992; Eisenberg et al. 1997), which combines secondary structure, solvent accessibility, and polarity of residue environments. ProsaII (Sippl 1993), which is based on a combination of a pairwise statistical potential and a solvation term, is also applied extensively in model evaluation. Other methods include the Errat program (Colovos and Yeates 1993), which considers distributions of nonbonded atoms according to atom type and distance, and the energy strain method (Maiorov and Abagyan 1998), which uses differences from average residue energies in different environments to indicate which parts of a protein structure might be problematic. Melo and Feytmans (1998) use an atomic pairwise potential and a surface-based solvation potential (both knowledge-based) to evaluate protein structures. Apart from the energy strain method, which is a semiempirical approach based on the ECEPP3 force field (Nemethy et al. 1992), all of the local methods listed above are based on statistical potentials. A conceptually distinct approach is the ProQres method, which was very recently introduced by Wallner and Elofsson (2006). ProQres is based on a neural network that combines structural features to distinguish correct from incorrect regions. ProQres was shown to outperform earlier methodologies based on statistical approaches (Verify3D, ProsaII, and Errat). The data presented in Wallner and Elofsson's study suggests that their machine-learning approach based on structural features is indeed superior to statistics-based methods. However, the knowledge-based methods examined in their work, Verify3D (Luthy et al. 1992; Eisenberg et al. 1997), Prosa (Sippl 1993), and Errat (Colovos and Yeates 1993), are not based on newer statistical potentials.

Benchmarking

[edit]

Several large-scale benchmarking efforts have been made to assess the relative quality of various current homology modeling methods. Critical Assessment of Structure Prediction (CASP) is a community-wide prediction experiment that runs every two years during the summer months and challenges prediction teams to submit structural models for a number of sequences whose structures have recently been solved experimentally but have not yet been published. Its partner Critical Assessment of Fully Automated Structure Prediction (CAFASP) has run in parallel with CASP but evaluates only models produced via fully automated servers. Continuously running experiments that do not have prediction 'seasons' focus mainly on benchmarking publicly available webservers. LiveBench and EVA run continuously to assess participating servers' performance in prediction of imminently released structures from the PDB. CASP and CAFASP serve mainly as evaluations of the state of the art in modeling, while the continuous assessments seek to evaluate the model quality that would be obtained by a non-expert user employing publicly available tools.

Accuracy

[edit]

The accuracy of the structures generated by homology modeling is highly dependent on the sequence identity between target and template. Above 50% sequence identity, models tend to be reliable, with only minor errors in side chain packing and rotameric state, and an overall RMSD between the modeled and the experimental structure falling around 1 Å. This error is comparable to the typical resolution of a structure solved by NMR. In the 30–50% identity range, errors can be more severe and are often located in loops. Below 30% identity, serious errors occur, sometimes resulting in the basic fold being mis-predicted.[14] This low-identity region is often referred to as the "twilight zone" within which homology modeling is extremely difficult, and to which it is possibly less suited than fold recognition methods.[24]

At high sequence identities, the primary source of error in homology modeling derives from the choice of the template or templates on which the model is based, while lower identities exhibit serious errors in sequence alignment that inhibit the production of high-quality models.[7] It has been suggested that the major impediment to quality model production is inadequacies in sequence alignment, since "optimal" structural alignments between two proteins of known structure can be used as input to current modeling methods to produce quite accurate reproductions of the original experimental structure.[25]

Attempts have been made to improve the accuracy of homology models built with existing methods by subjecting them to molecular dynamics simulation in an effort to improve their RMSD to the experimental structure. However, current force field parameterizations may not be sufficiently accurate for this task, since homology models used as starting structures for molecular dynamics tend to produce slightly worse structures.[26] Slight improvements have been observed in cases where significant restraints were used during the simulation.[27]

Sources of error

[edit]

The two most common and large-scale sources of error in homology modeling are poor template selection and inaccuracies in target-template sequence alignment.[7][28] Controlling for these two factors by using a structural alignment, or a sequence alignment produced on the basis of comparing two solved structures, dramatically reduces the errors in final models; these "gold standard" alignments can be used as input to current modeling methods to produce quite accurate reproductions of the original experimental structure.[25] Results from the most recent CASP experiment suggest that "consensus" methods collecting the results of multiple fold recognition and multiple alignment searches increase the likelihood of identifying the correct template; similarly, the use of multiple templates in the model-building step may be worse than the use of the single correct template but better than the use of a single suboptimal one.[28] Alignment errors may be minimized by the use of a multiple alignment even if only one template is used, and by the iterative refinement of local regions of low similarity.[3][12] A lesser source of model errors are errors in the template structure. The PDBREPORT Archived 2007-05-31 at the Wayback Machine database lists several million, mostly very small but occasionally dramatic, errors in experimental (template) structures that have been deposited in the PDB.

Serious local errors can arise in homology models where an insertion or deletion mutation or a gap in a solved structure result in a region of target sequence for which there is no corresponding template. This problem can be minimized by the use of multiple templates, but the method is complicated by the templates' differing local structures around the gap and by the likelihood that a missing region in one experimental structure is also missing in other structures of the same protein family. Missing regions are most common in loops where high local flexibility increases the difficulty of resolving the region by structure-determination methods. Although some guidance is provided even with a single template by the positioning of the ends of the missing region, the longer the gap, the more difficult it is to model. Loops of up to about 9 residues can be modeled with moderate accuracy in some cases if the local alignment is correct.[3] Larger regions are often modeled individually using ab initio structure prediction techniques, although this approach has met with only isolated success.[29]

The rotameric states of side chains and their internal packing arrangement also present difficulties in homology modeling, even in targets for which the backbone structure is relatively easy to predict. This is partly due to the fact that many side chains in crystal structures are not in their "optimal" rotameric state as a result of energetic factors in the hydrophobic core and in the packing of the individual molecules in a protein crystal.[30] One method of addressing this problem requires searching a rotameric library to identify locally low-energy combinations of packing states.[31] It has been suggested that a major reason that homology modeling so difficult when target-template sequence identity lies below 30% is that such proteins have broadly similar folds but widely divergent side chain packing arrangements.[4]

Utility

[edit]

Uses of the structural models include protein–protein interaction prediction, protein–protein docking, molecular docking, and functional annotation of genes identified in an organism's genome.[32] Even low-accuracy homology models can be useful for these purposes, because their inaccuracies tend to be located in the loops on the protein surface, which are normally more variable even between closely related proteins. The functional regions of the protein, especially its active site, tend to be more highly conserved and thus more accurately modeled.[14]

Homology models can also be used to identify subtle differences between related proteins that have not all been solved structurally. For example, the method was used to identify cation binding sites on the Na+/K+ ATPase and to propose hypotheses about different ATPases' binding affinity.[33] Used in conjunction with molecular dynamics simulations, homology models can also generate hypotheses about the kinetics and dynamics of a protein, as in studies of the ion selectivity of a potassium channel.[34] Large-scale automated modeling of all identified protein-coding regions in a genome has been attempted for the yeast Saccharomyces cerevisiae, resulting in nearly 1000 quality models for proteins whose structures had not yet been determined at the time of the study, and identifying novel relationships between 236 yeast proteins and other previously solved structures.[35]

See also

[edit]

References

[edit]
Revisions and contributorsEdit on WikipediaRead on Wikipedia

Homology modeling

View on Grokipedia
from Grokipedia
Homology modeling, also known as comparative modeling, is a computational method in structural bioinformatics for predicting the three-dimensional (3D) structure of a target protein based on its sequence and the known 3D of a homologous template protein that shares evolutionary ancestry. This approach exploits the fundamental principle that proteins with sufficient sequence similarity—typically greater than 30% identity—adopt comparable folds due to conserved evolutionary relationships, where structural conservation often outpaces sequence divergence. As one of the most established techniques in , it has been instrumental in filling gaps in the (PDB) by enabling the modeling of sequences without experimentally determined structures, particularly when a suitable template is available. The origins of homology modeling trace back over half a century to early studies on protein folding and sequence-structure relationships in the 1960s and 1970s, but it gained practical momentum in the 1980s with the expansion of the PDB and seminal works demonstrating the feasibility of template-based modeling. Key advancements occurred through biennial Critical Assessment of Structure Prediction (CASP) experiments starting in 1994, which benchmarked and refined the method's accuracy, revealing that models can achieve root-mean-square deviation (RMSD) values below 1 Å for high-identity targets. By the 1990s, tools like MODELLER formalized the process, integrating statistical and physics-based refinements to address challenges such as alignment errors and loop flexibility. The core workflow of homology modeling involves several sequential steps to construct and validate a reliable model. First, a suitable template is identified from structural databases like the PDB using sequence similarity searches (e.g., via BLAST or PSI-BLAST). Next, the target sequence is aligned to the template to conserved regions, followed by backbone coordinate transfer, loop modeling for variable regions (using methods like database scanning or ab initio generation), and side-chain packing with rotamer libraries (e.g., SCWRL). The model is then refined through energy minimization or simulations to resolve steric clashes, and finally validated using metrics such as Ramachandran plots, PROCHECK scores, or stereochemical assessments to ensure physical realism. Homology modeling's significance lies in its accessibility and efficiency compared to experimental methods like or cryo-electron microscopy, making it a for applications in , functional annotation, and structural . In pharmaceuticals, it facilitates structure-based by predicting binding sites for ligands, as seen in modeling G-protein coupled receptors (GPCRs) for development and of inhibitors against targets like histone deacetylases (HDACs). Despite limitations—such as reduced accuracy for low-identity templates (below 30%) or membrane proteins—ongoing integrations with and (e.g., ) continue to enhance its precision, even as methods like complement it for challenging cases.

Introduction

Definition and Principles

Homology modeling is a computational technique used to predict the three-dimensional (3D) atomic of a target protein by leveraging the known experimental of a homologous template protein. This method relies on the fundamental evolutionary that protein structures are more conserved than their sequences over time, allowing structural similarities to persist even as sequences diverge. At its core, homology modeling assumes that proteins sharing a common evolutionary ancestry—termed homologs—adopt similar folds due to shared descent, in contrast to analogous structures that arise from without a common ancestor. A key indicator of reliable homology is sequence identity, typically exceeding 30%, which correlates with structural similarity and model accuracy; this percentage is calculated as: Sequence Identity (%)=(Number of identical residuesTotal number of aligned residues)×100\text{Sequence Identity (\%)} = \left( \frac{\text{Number of identical residues}}{\text{Total number of aligned residues}} \right) \times 100 Below this threshold, predictions become less dependable due to increased structural divergence. The basic workflow of homology modeling encompasses high-level steps: identifying suitable template structures through sequence similarity searches, aligning the target and template sequences, constructing the atomic model based on the template's coordinates, and validating the resulting structure for consistency. This approach is particularly valuable for proteins with functional similarities, as it extrapolates conserved structural features to infer the target's tertiary fold.

Historical Development

Homology modeling emerged in the late as one of the earliest computational approaches to , building on the observation that proteins with similar s often adopt similar three-dimensional folds. The foundational work was reported by Browne and colleagues in 1969, who manually constructed a model of bovine by aligning its to that of hen egg-white lysozyme—a structurally known homolog—and fitting coordinates through using physical models. This coordinate-fitting method represented an initial profile-based strategy, relying on similarity to infer structural conservation, though it was labor-intensive and limited by the scarcity of available structures. The 1971 establishment of the (PDB) marked a pivotal shift, providing a centralized repository for experimentally determined structures that grew from just seven entries to thousands by the , enabling more systematic database-driven searches for homologous templates rather than ad hoc manual alignments. In the , quantitative insights advanced the field: Chothia and Lesk's 1986 analysis of homologous protein pairs demonstrated a nonlinear relationship between sequence divergence and structural deviation, establishing that even distantly related sequences (up to 30% identity) could retain core folds, thus justifying homology modeling for a broader range of targets. The 1990s saw the rise of automated tools, transforming homology modeling from manual processes to computational pipelines. A landmark was the development of MODELLER in 1993 by Sali and Blundell, which automated model generation by satisfying spatial restraints derived from template alignments and empirical potentials, significantly improving efficiency and accuracy. Concurrently, the inaugural Critical Assessment of Structure Prediction () experiment in 1994 introduced blind benchmarking, revealing homology modeling's strengths for targets with detectable homologs while highlighting needs for better alignment and loop handling; subsequent CASPs through the decade refined these aspects and solidified the method's role. By the 2000s, refinements focused on challenging regions, such as loop modeling, with Fiser et al.'s 2000 extensions to MODELLER incorporating statistical potentials for loop conformation prediction, enhancing overall model quality. Homology modeling remained the dominant technique for structure prediction into the , applicable to over 50% of new sequences due to expanding structural databases, until advances like in 2020 demonstrated superior de novo capabilities for cases without clear homologs. Subsequent advancements, such as 3 in 2024, have further expanded capabilities to model protein interactions with other biomolecules.

Prerequisites

Protein Structure Fundamentals

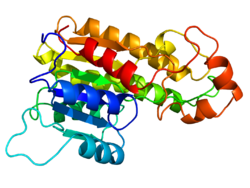
Proteins are macromolecules composed of amino acids linked by peptide bonds, and their three-dimensional structures are crucial for function. The structure of a protein is organized into four hierarchical levels. At the primary level, the structure is defined by the linear sequence of amino acids, which determines all higher-order folding. Secondary structure elements, such as alpha helices and beta sheets, arise from hydrogen bonding between the backbone carbonyl oxygen and amide hydrogen atoms within the polypeptide chain. Tertiary structure represents the overall three-dimensional fold of a single polypeptide chain, stabilized by hydrophobic interactions that bury nonpolar residues in the core, as well as electrostatic interactions, van der Waals forces, and disulfide bonds between cysteine residues. Quaternary structure occurs in proteins with multiple subunits, where individual chains assemble into a functional complex, often further stabilized by the same types of interactions as in tertiary structure. The folding of a protein from its primary into a native tertiary structure is governed by thermodynamic principles. posits that the native structure is the one with the lowest free energy, uniquely determined by the under physiological conditions, as demonstrated by experiments refolding denatured . However, highlights the immense conformational search space—a single 100-residue protein could theoretically adopt more than 10^47 possible conformations—yet proteins fold rapidly in milliseconds to seconds, resolved by the concept of an energy funnel where the landscape guides folding toward the native state via partially folded intermediates. , molecular chaperones such as and assist folding by preventing aggregation and promoting correct pathways, particularly for larger proteins. Key geometric constraints define allowable protein conformations. The maps the backbone dihedral angles phi (φ) and psi (ψ), revealing favored regions for alpha helices (φ ≈ -60°, ψ ≈ -45°), beta sheets (φ ≈ -120°, ψ ≈ +120°), and other motifs, based on steric hindrance from side chains and backbone atoms; disallowed regions occupy about 40% of the plot due to atomic clashes. In folded proteins, the hydrophobic core exhibits high packing density, with solvent-accessible surface area () typically reduced by 80-90% compared to the unfolded state, as nonpolar residues minimize exposure to . Evolutionarily related proteins often conserve these tertiary folds despite sequence divergence, underscoring structure's role in function. Experimental structures are stored in the (PDB) format, an ASCII file containing atomic coordinates (x, y, z in angstroms), residue identifiers, and metadata like resolution from or cryo-EM; each entry includes a header with experimental details and models for ensembles. Visualization tools like PyMOL render these coordinates in 3D, allowing rotation, zooming, and highlighting of secondary elements or surfaces for analysis.

Sequence Homology Concepts

In protein sequences, homology denotes a relationship of common evolutionary ancestry, resulting in features due to shared descent from a . This conservation arises because functional constraints limit divergence, preserving key motifs across related proteins. Homologous proteins are classified into orthologs, which evolve via events from a single ancestral in different lineages, and paralogs, which arise from within a followed by divergence. In contrast, sequence similarity refers merely to observable matches in composition or order, representing a statistical measure without implying evolutionary relatedness; homology requires evidence of ancestry beyond mere resemblance. Detecting sequence homology relies on alignment-based metrics that assess significance amid random variation. Tools like BLAST and its iterative extension PSI-BLAST perform local alignments to identify similar regions, using bit scores to quantify match quality while E-values estimate the probability of chance occurrences in a database search, with thresholds below 0.01 typically indicating reliable homology. However, challenges emerge in the "twilight zone" of sequence identity below 30%, where alignments become unreliable for inferring homology due to saturation of substitutions and structural divergence, often requiring advanced profile-based methods for detection. Sequence conservation patterns reflect evolutionary pressures, with invariant residues frequently occurring in active sites to maintain catalytic or binding functions, as identified through phylogenetic analyses like the evolutionary trace method. Variable regions, such as surface loops, tolerate greater substitution due to reduced functional constraints, allowing while core structural elements remain stable. To quantify evolutionary divergence accounting for multiple unobserved substitutions, the Poisson correction for proteins is used:
d=−ln⁡(1−p)d = -\ln(1 - p)
where pp represents the proportion of observed differences between aligned residues (gaps excluded via pairwise deletion), providing an estimate of substitutions per site. In homology modeling, higher sequence identity strongly correlates with structural similarity, as measured by root-mean-square deviation (RMSD) of atomic positions; for identities exceeding 40%, modeled structures typically achieve RMSD values below 2 Å relative to native templates, enabling reliable inference of tertiary folds from conserved cores. This relationship underpins the rationale for homology modeling, where predicts structural conservation despite moderate evolutionary distances.

Modeling Workflow

Template Selection

Template selection is a critical initial step in homology modeling, involving the identification of experimentally determined protein structures that serve as scaffolds for the target protein's three-dimensional model. These templates are sourced primarily from the (PDB), the central repository for atomic-level biomolecular structures, which as of November 2025 contains over 244,000 entries and continues to grow with thousands of new structures released annually. Specialized databases such as (Structural Classification of Proteins) and CATH (Class, Architecture, Topology, and Homologous superfamily) provide hierarchical classifications of protein folds, aiding in the selection of evolutionarily related templates by grouping structures into superfamilies based on structural similarity beyond sequence alone. Search methods for templates fall into sequence-based and structure-based categories. Sequence-based approaches utilize profile-profile alignments to detect homologous sequences with higher sensitivity than pairwise comparisons; prominent tools include HHblits, which performs iterative (HMM)-HMM searches against large databases like , and JackHMMER, which iteratively builds HMMs from the target to query sequence databases. Structure-based methods, particularly useful for remote homologs, employ fold recognition through threading algorithms that evaluate how well the target fits known folds; I-TASSER, for instance, integrates multiple threading programs to rank templates by alignment scores and structural compatibility. Templates are selected based on stringent criteria to ensure model reliability, including sequence identity exceeding 30%—a threshold associated with conserved core structures—coverage of at least 70% of the target sequence to minimize gaps, resolution better than 2.5 for atomic accuracy, and low B-factors indicating well-ordered regions. Often, multiple templates are chosen to capture conformational variations, enabling consensus modeling that averages alignments for improved accuracy. Advanced techniques enhance template detection for cases with low sequence similarity. Co-evolution analysis derived from multiple sequence alignments (MSAs) of homologous proteins identifies residue contacts that reveal distant structural relationships, extending the detectable homology horizon. Additionally, deep learning-based profiles, such as those from protein models, incorporate evolutionary and structural signals to improve remote homolog detection, outperforming traditional methods by over 10% in sensitivity on benchmark datasets.

Target-Template Alignment

Target-template alignment is a critical step in homology modeling, where the sequence of the target protein is aligned with that of the selected template to establish residue correspondences that guide subsequent structural modeling. This process typically begins with pairwise sequence alignment methods, which compute optimal alignments between two sequences using dynamic programming algorithms. The Needleman-Wunsch algorithm performs global alignment, seeking to align the entire lengths of the target and template sequences, while the Smith-Waterman algorithm conducts local alignment, focusing on the highest-scoring subsequence matches, which is particularly useful when the proteins share only conserved domains. For improved accuracy, especially with evolutionarily divergent sequences, profile-based alignments are preferred over simple pairwise methods. These involve constructing position-specific scoring matrices (PSSMs) or hidden Markov models (HMMs) from multiple sequence alignments (MSAs) of the target and template families, capturing conserved patterns across homologs. Tools like Clustal Omega generate MSAs progressively, enabling profile-profile comparisons that enhance sensitivity in detecting remote homologs. In homology modeling, alignments are often refined with structural and predictive information to account for three-dimensional constraints. Structural alignments, such as those produced by TM-align, superpose the template's atomic coordinates and realign sequences based on spatial proximity, helping to resolve ambiguities in regions with insertions or deletions (). Secondary structure predictions from tools like PSIPRED are incorporated to penalize mismatches between predicted target helices or sheets and the template's known structure, guiding more biologically plausible alignments. Indel penalties are typically affine, comprising a higher cost for gap opening and a lower cost for gap extension, to discourage excessive fragmentation while allowing realistic loop insertions. Alignment quality is evaluated using scoring functions that quantify substitution likelihoods and penalize gaps. Substitution scores are derived from empirical matrices like BLOSUM (Block Substitution Matrix), which are clustered from conserved protein blocks to reflect observed evolutionary exchanges, or PAM (Point Accepted Mutation) matrices, based on closely related sequences extrapolated for divergence. The overall alignment score SS is calculated as the sum of substitution scores minus gap penalties: S=∑i,js(ai,bj)−(go+ge⋅l)S = \sum_{i,j} s(a_i, b_j) - (g_o + g_e \cdot l) where s(ai,bj)s(a_i, b_j) is the score for aligning residues aia_i and bjb_j, gog_o is the gap opening penalty, geg_e is the gap extension penalty, and ll is the gap length. BLOSUM62, for instance, is widely used due to its balance for alignments around 30% identity. Challenges arise particularly in low-identity alignments (below 30%), where sequence similarity enters the "twilight zone," leading to multiple equally plausible alignments and potential errors in residue mapping that propagate to model inaccuracy. To address this, iterative refinement strategies, as implemented in software like MODELLER, repeatedly optimize the alignment by satisfying spatial restraints derived from the template structure and adjusting for stereochemical feasibility. These methods, rooted in comparative modeling principles, have been shown to improve alignment reliability even for templates with 20-40% identity.

Backbone Modeling

In homology modeling, the construction of the protein backbone for the conserved core regions begins with the direct transfer of structural coordinates from the identified template structure to the corresponding aligned residues in the target sequence. This process relies on the target-template alignment to map equivalent residues, allowing the backbone atoms (typically N, Cα, C, and O) of the template to be copied to the model, preserving the local geometry where sequence and structural similarity is high. For aligned residues in the core, the phi (φ) and psi (ψ) dihedral angles from the template are adopted to maintain the secondary structure elements such as alpha-helices and beta-sheets. To ensure proper spatial orientation of conserved segments, rigid-body superposition is applied, involving least-squares fitting to align the template's core framework with the target's expected position. This method minimizes the differences in atomic positions across the superimposed atoms, often focusing on Cα atoms in secondary regions to handle the framework (conserved core) separately from variable regions. The of this fit is quantified using the root-mean-square deviation (RMSD), calculated as 1N∑i=1N(xi−yi)2\sqrt{\frac{1}{N} \sum_{i=1}^{N} ( \mathbf{x}_i - \mathbf{y}_i )^2}
Add your contribution
Related Hubs
User Avatar
No comments yet.