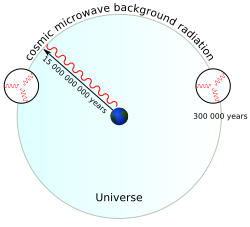
The horizon problem (also known as the homogeneity problem) is a cosmological fine-tuning problem within the Big Bang model of the universe. It arises due to the difficulty in explaining the observed homogeneity of causally disconnected regions of space in the absence of a mechanism that sets the same initial conditions everywhere. It was first pointed out by Wolfgang Rindler in 1956.

The most commonly accepted solution is cosmic inflation. Different solutions propose a cyclic universe or a variable speed of light.

The distances of observable objects in the night sky correspond to times in the past. We use the light-year (the distance light can travel in the time of one Earth year) to describe these cosmological distances. A galaxy measured at ten billion light-years appears to us as it was ten billion years ago, because the light has taken that long to travel to the observer. If one were to look at a galaxy ten billion light-years away in one direction and another in the opposite direction, the total distance between them is twenty billion light-years. This means that the light from the first has not yet reached the second because the universe is only about 13.8 billion years old. In a more general sense, there are portions of the universe that are visible to us, but invisible to each other, outside each other's respective particle horizons.

In accepted relativistic physical theories, no information can travel faster than the speed of light. In this context, "information" means "any sort of physical interaction". For instance, heat will naturally flow from a hotter area to a cooler one, and in physics terms, this is one example of information exchange. Given the example above, the two galaxies in question cannot have shared any sort of information; they are not in causal contact. In the absence of common initial conditions, one would expect, then, that their physical properties would be different, and more generally, that the universe as a whole would have varying properties in causally disconnected regions.

Contrary to this expectation, the observations of the cosmic microwave background (CMB) and galaxy surveys show that the observable universe is nearly isotropic, which, through the Copernican principle, also implies homogeneity. CMB sky surveys show that the temperatures of the CMB are coordinated to a level of ${\displaystyle \Delta T/T\approx 10^{-5},}$ where ${\displaystyle \Delta T}$ is the difference between the observed temperature in a region of the sky and the average temperature of the sky ${\displaystyle T}$. This coordination implies that the entire sky, and thus the entire observable universe, must have been causally connected long enough for the universe to come into thermal equilibrium.

According to the Big Bang model, as the density of the expanding universe dropped, it eventually reached a temperature where photons fell out of thermal equilibrium with matter; they decoupled from the electron-proton plasma and began free-streaming across the universe. This moment in time is referred to as the epoch of Recombination, when electrons and protons became bound to form electrically neutral hydrogen; without free electrons to scatter the photons, the photons began free-streaming. This epoch is observed through the CMB. Since we observe the CMB as a background to objects at a smaller redshift, we describe this epoch as the transition of the universe from opaque to transparent. The CMB physically describes the 'surface of last scattering' as it appears to us as a surface, or a background, as shown in the figure below.

Note we use conformal time in the following diagrams. Conformal time describes the amount of time it would take a photon to travel from the location of the observer to the farthest observable distance (if the universe stopped expanding right now).

The decoupling, or the last scattering, is thought to have occurred about 300,000 years after the Big Bang, or at a redshift of about ${\displaystyle z_{rec}\approx 1100}$. We can determine both the approximate angular diameter of the universe and the physical size of the particle horizon that had existed at this time.