Metallic mean

Golden ratio within the pentagram (φ = red/ green = green/blue = blue/purple) and silver ratio within the octagon.

The defining equation ${\textstyle x=n+{\frac {1}{x}}}$ of the nth metallic mean induces the following geometrical interpretation.

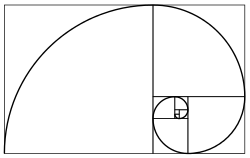
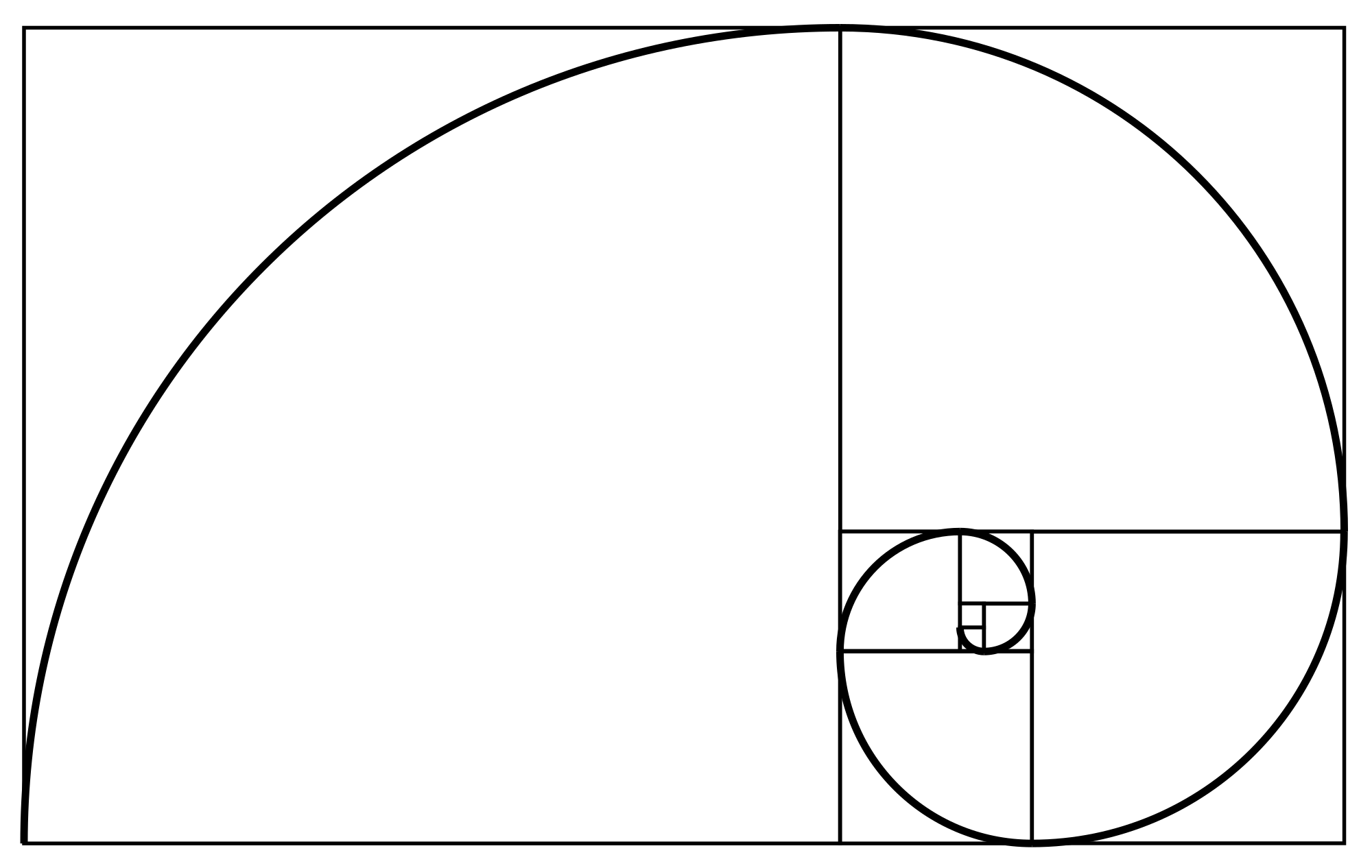
Consider a rectangle such that the ratio of its length L to its width W is the nth metallic ratio. If one remove from this rectangle n squares of side length W, one gets a rectangle similar to the original rectangle; that is, a rectangle with the same ratio of the length to the width (see figures).

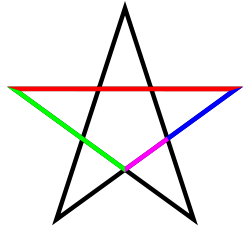
Some metallic means appear as segments in the figure formed by a regular polygon and its diagonals. This is in particular the case for the golden ratio and the pentagon, and for the silver ratio and the octagon; see figures.

This section does not cite any sources. Please help improve this section by adding citations to reliable sources. Unsourced material may be challenged and removed. (August 2020) (Learn how and when to remove this message)

Denoting by ${\displaystyle S_{m}}$ the metallic mean of m one has

${\displaystyle S_{m}^{n}=K_{n}S_{m}+K_{n-1},}$

where the numbers ${\displaystyle K_{n}}$ are defined recursively by the initial conditions K₀ = 0 and K₁ = 1, and the recurrence relation

${\displaystyle K_{n}=mK_{n-1}+K_{n-2}.}$

Proof: The equality is immediately true for ${\displaystyle n=1.}$ The recurrence relation implies ${\displaystyle K_{2}=m,}$ which makes the equality true for ${\displaystyle k=2.}$ Supposing the equality true up to ${\displaystyle n-1,}$ one has

${\displaystyle {\begin{aligned}S_{m}^{n}&=mS_{m}^{n-1}+S_{m}^{n-2}&&{\text{(defining equation)}}\\&=m(K_{n-1}S_{n}+K_{n-2})+(K_{n-2}S_{m}+K_{n-3})&&{\text{(recurrence hypothesis)}}\\&=(mK_{n-1}+K_{n-2})S_{n}+(mK_{n-2}+K_{n-3})&&{\text{(regrouping)}}\\&=K_{n}S_{m}+K_{n-1}&&{\text{(recurrence on }}K_{n}).\end{aligned}}}$

End of the proof.

One has also ^{[citation needed]}

${\displaystyle K_{n}={\frac {S_{m}^{n+1}-(m-S_{m})^{n+1}}{\sqrt {m^{2}+4}}}.}$

The odd powers of a metallic mean are themselves metallic means. More precisely, if n is an odd natural number, then ${\displaystyle S_{m}^{n}=S_{M_{n}},}$ where ${\displaystyle M_{n}}$ is defined by the recurrence relation ${\displaystyle M_{n}=mM_{n-1}+M_{n-2}}$ and the initial conditions ${\displaystyle M_{0}=2}$ and ${\displaystyle M_{1}=m.}$

Proof: Let ${\displaystyle a=S_{m}}$ and ${\displaystyle b=-1/S_{m}.}$ The definition of metallic means implies that ${\displaystyle a+b=m}$ and ${\displaystyle ab=-1.}$ Let ${\displaystyle M_{n}=a^{n}+b^{n}.}$ Since ${\displaystyle a^{n}b^{n}=(ab)^{n}=-1}$ if n is odd, the power ${\displaystyle a^{n}}$ is a root of ${\displaystyle x^{2}-M_{n}-1=0.}$ So, it remains to prove that ${\displaystyle M_{n}}$ is an integer that satisfies the given recurrence relation. This results from the identity

${\displaystyle {\begin{aligned}a^{n}+b^{n}&=(a+b)(a^{n-1}+b^{n-1})-ab(a^{n-2}+a^{n-2})\\&=m(a^{n-1}+b^{n-1})+(a^{n-2}+a^{n-2}).\end{aligned}}}$

This completes the proof, given that the initial values are easy to verify.

In particular, one has

${\displaystyle {\begin{aligned}S_{m}^{3}&=S_{m^{3}+3m}\\S_{m}^{5}&=S_{m^{5}+5m^{3}+5m}\\S_{m}^{7}&=S_{m^{7}+7m^{5}+14m^{3}+7m}\\S_{m}^{9}&=S_{m^{9}+9m^{7}+27m^{5}+30m^{3}+9m}\\S_{m}^{11}&=S_{m^{11}+11m^{9}+44m^{7}+77m^{5}+55m^{3}+11m}\end{aligned}}}$

and, in general,^{[citation needed]}

${\displaystyle S_{m}^{2n+1}=S_{M},}$

where

${\displaystyle M=\sum _{k=0}^{n}{{2n+1} \over {2k+1}}{{n+k} \choose {2k}}m^{2k+1}.}$

For even powers, things are more complicated. If n is a positive even integer then^{[citation needed]}

${\displaystyle {S_{m}^{n}-\left\lfloor S_{m}^{n}\right\rfloor }=1-S_{m}^{-n}.}$

Additionally,^{[citation needed]}

${\displaystyle {1 \over {S_{m}^{4}-\left\lfloor S_{m}^{4}\right\rfloor }}+\left\lfloor S_{m}^{4}-1\right\rfloor =S_{\left(m^{4}+4m^{2}+1\right)}}$

${\displaystyle {1 \over {S_{m}^{6}-\left\lfloor S_{m}^{6}\right\rfloor }}+\left\lfloor S_{m}^{6}-1\right\rfloor =S_{\left(m^{6}+6m^{4}+9m^{2}+1\right)}.}$

For the square of a metallic ratio we have:${\displaystyle S_{m}^{2}=[m{\sqrt {m^{2}+4}}+(m+2)]/2=(p+{\sqrt {p^{2}+4}})/2}$

where ${\displaystyle p=m{\sqrt {m^{2}+4}}}$ lies strictly between ${\displaystyle m^{2}+1}$ and ${\displaystyle m^{2}+2}$. Therefore

${\displaystyle S_{m^{2}+1}<S_{m}^{2}<S_{m^{2}+2}}$

One may define the metallic mean ${\displaystyle S_{-n}}$ of a negative integer −n as the positive solution of the equation ${\displaystyle x^{2}-(-n)x-1.}$ The metallic mean of −n is the multiplicative inverse of the metallic mean of n:

${\displaystyle S_{-n}={\frac {1}{S_{n}}}.}$

Another generalization consists of changing the defining equation from ${\displaystyle x^{2}-nx-1=0}$ to ${\displaystyle x^{2}-nx-c=0}$. If

${\displaystyle R={\frac {n\pm {\sqrt {n^{2}+4c}}}{2}},}$

is any root of the equation, one has

${\displaystyle R-n={\frac {c}{R}}.}$

The silver mean of m is also given by the integral^[4]

${\displaystyle S_{m}=\int _{0}^{m}{\left({x \over {2{\sqrt {x^{2}+4}}}}+{{m+2} \over {2m}}\right)}\,dx.}$

Another form of the metallic mean is^[4]

${\displaystyle {\frac {n+{\sqrt {n^{2}+4}}}{2}}=e^{\operatorname {arsinh(n/2)} }.}$

A tangent half-angle formula gives $${\displaystyle \cot \theta ={\frac {\cot ^{2}{\frac {\theta }{2}}-1}{2\cot {\frac {\theta }{2}}}}}$$ which can be rewritten as $${\displaystyle \cot ^{2}{\frac {\theta }{2}}-(2\cot \theta )\cot {\frac {\theta }{2}}-1=0\,.}$$ That is, for the positive value of ${\textstyle \cot {\frac {\theta }{2}}}$, the metallic mean $${\displaystyle S_{2\cot \theta }=\cot {\frac {\theta }{2}}\,,}$$ which is especially meaningful when ${\textstyle 2\cot \theta }$ is a positive integer, as it is with some Pythagorean triangles.

For a primitive Pythagorean triple, a² + b² = c², with positive integers a < b < c that are relatively prime, if the difference between the hypotenuse c and longer leg b is 1, 2 or 8 then the Pythagorean triangle exhibits a metallic mean. Specifically, the cotangent of one quarter of the smaller acute angle of the Pythagorean triangle is a metallic mean.^[5]

More precisely, for a primitive Pythagorean triple (a, b, c) with a < b < c, the smaller acute angle α satisfies $${\displaystyle \tan {\frac {\alpha }{2}}={\frac {c-b}{a}}\,.}$$ When c − b ∈ {1, 2, 8}, we will always get that $${\displaystyle n=2\cot {\frac {\alpha }{2}}={\frac {2a}{c-b}}}$$ is an integer and that $${\displaystyle \cot {\frac {\alpha }{4}}=S_{n}\,,}$$ the n-th metallic mean.

The reverse direction also works. For n ≥ 5, the primitive Pythagorean triple that gives the n-th metallic mean is given by (n, n²/4 − 1, n²/4 + 1) if n is a multiple of 4, is given by (n/2, (n² − 4)/8, (n² + 4)/8) if n is even but not a multiple of 4, and is given by (4n, n² − 4, n² + 4) if n is odd. For example, the primitive Pythagorean triple (20, 21, 29) gives the 5th metallic mean; (3, 4, 5) gives the 6th metallic mean; (28, 45, 53) gives the 7th metallic mean; (8, 15, 17) gives the 8th metallic mean; and so on.

• Constant
• Mean
• Ratio
• Plastic ratio