Hubbry Logo
Piecewise linear functionPiecewise linear functionMain
Open search
Piecewise linear function
Community hub
Piecewise linear function
logo
7 pages, 0 posts
0 subscribers
Be the first to start a discussion here.
Be the first to start a discussion here.
Contribute something
Piecewise linear function
Piecewise linear function
Piecewise linear function
View on Wikipedia
from Wikipedia

In mathematics, a piecewise linear or segmented function is a real-valued function of a real variable, whose graph is composed of straight-line segments.[1]

Definition

[edit]

A piecewise linear function is a function defined on a (possibly unbounded) interval of real numbers, such that there is a collection of intervals on each of which the function is an affine function. (Thus "piecewise linear" is actually defined to mean "piecewise affine".) If the domain of the function is compact, there needs to be a finite collection of such intervals; if the domain is not compact, it may either be required to be finite or to be locally finite in the reals.

Examples

[edit]
A continuous piecewise linear function

The function defined by

is piecewise linear with four pieces. The graph of this function is shown to the right. Since the graph of an affine(*) function is a line, the graph of a piecewise linear function consists of line segments and rays. The x values (in the above example −3, 0, and 3) where the slope changes are typically called breakpoints, changepoints, threshold values or knots. As in many applications, this function is also continuous. The graph of a continuous piecewise linear function on a compact interval is a polygonal chain.

(*) A linear function satisfies by definition and therefore in particular ; functions whose graph is a straight line are affine rather than linear.

There are other examples of piecewise linear functions:

Fitting to a curve

[edit]
A function (blue) and a piecewise linear approximation to it (red)

An approximation to a known curve can be found by sampling the curve and interpolating linearly between the points. An algorithm for computing the most significant points subject to a given error tolerance has been published.[3]

Fitting to data

[edit]
Main article: Segmented regression

If partitions, and then breakpoints, are already known, linear regression can be performed independently on these partitions. However, continuity is not preserved in that case, and also there is no unique reference model underlying the observed data. A stable algorithm with this case has been derived.[4]

If partitions are not known, the residual sum of squares can be used to choose optimal separation points.[5] However efficient computation and joint estimation of all model parameters (including the breakpoints) may be obtained by an iterative procedure[6] currently implemented in the package segmented[7] for the R language.

A variant of decision tree learning called model trees learns piecewise linear functions.[8]

Generalizations

[edit]
A piecewise linear function of two arguments (top) and the convex polytopes on which it is linear (bottom)

The notion of a piecewise linear function makes sense in several different contexts. Piecewise linear functions may be defined on n-dimensional Euclidean space, or more generally any vector space or affine space, as well as on piecewise linear manifolds and simplicial complexes (see simplicial map). In each case, the function may be real-valued, or it may take values from a vector space, an affine space, a piecewise linear manifold, or a simplicial complex. (In these contexts, the term “linear” does not refer solely to linear transformations, but to more general affine linear functions.)

In dimensions higher than one, it is common to require the domain of each piece to be a polygon or polytope. This guarantees that the graph of the function will be composed of polygonal or polytopal pieces.

Splines generalize piecewise linear functions to higher-order polynomials, which are in turn contained in the category of piecewise-differentiable functions, PDIFF.

Specializations

[edit]

Important sub-classes of piecewise linear functions include the continuous piecewise linear functions and the convex piecewise linear functions. In general, for every n-dimensional continuous piecewise linear function , there is a

such that

[9]

If is convex and continuous, then there is a

such that

Applications

[edit]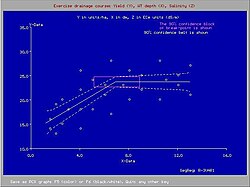
Crop response to depth of the watertable[10]
Example of crop response to soil salinity[11]

In agriculture piecewise regression analysis of measured data is used to detect the range over which growth factors affect the yield and the range over which the crop is not sensitive to changes in these factors.

The image on the left shows that at shallow watertables the yield declines, whereas at deeper (> 7 dm) watertables the yield is unaffected. The graph is made using the method of least squares to find the two segments with the best fit.

The graph on the right reveals that crop yields tolerate a soil salinity up to ECe = 8 dS/m (ECe is the electric conductivity of an extract of a saturated soil sample), while beyond that value the crop production reduces. The graph is made with the method of partial regression to find the longest range of "no effect", i.e. where the line is horizontal. The two segments need not join at the same point. Only for the second segment method of least squares is used.

See also

[edit]

Further reading

[edit]

References

[edit]
Revisions and contributorsEdit on WikipediaRead on Wikipedia

Piecewise linear function

View on Grokipedia
from Grokipedia
A piecewise linear function is a real-valued function defined on an interval of the real numbers, composed of a finite or of affine (linear plus constant) segments, each applied on a subinterval of the domain. These functions are characterized by their graphs, which consist of straight-line segments connected at breakpoints where the changes, allowing them to model behaviors that linear functions alone cannot capture, such as abrupt shifts in trends. While not all piecewise linear functions are continuous—discontinuities can occur at breakpoints—continuous variants form an important subclass, often used in applications requiring smooth transitions. Convex piecewise linear functions, where slopes are non-decreasing across segments, exhibit useful optimization properties, such as being minimizable over polyhedral sets. Common examples include the function ∣x∣|x|, which switches from slope -1 to +1 at x=0x = 0, the sawtooth function for periodic approximations, and the floor function ⌊x⌋\lfloor x \rfloor, though the latter is typically discontinuous. In higher dimensions, piecewise linear functions extend to domains divided into polyhedra, enabling multidimensional modeling. Piecewise linear functions find broad applications in and related fields, including to with changing trends, such as agricultural yield models, and piecewise linear regression to detect structural breaks in statistical . They are also essential in optimization, where they approximate nonlinear costs or objectives in mixed-integer formulations, and in for representing activation functions like ReLU in neural networks. In engineering, they model piecewise-linear networks for circuit analysis and .

Core Concepts

Definition

A piecewise linear function, more precisely termed a piecewise affine function in modern usage, is a mapping f:X→Rmf: X \to \mathbb{R}^m where X⊆RnX \subseteq \mathbb{R}^n is the domain, obtained by partitioning XX into a finite number of polyhedral sets {Pi}i∈I\{P_i\}_{i \in I} (the pieces) such that the interiors of the PiP_i are disjoint, their union covers XX, and ff restricts to an affine function on each piece PiP_i. On each PiP_i, the affine form is given by f(x)=Aix+bi,x∈Pi,f(x) = A_i x + b_i, \quad x \in P_i, where Ai∈Rm×nA_i \in \mathbb{R}^{m \times n} is a matrix and bi∈Rmb_i \in \mathbb{R}^m is a constant vector. This structure allows the function to exhibit linear behavior locally within each polyhedral region while enabling global nonlinearity through the partitioning. The terminology "piecewise linear" is often used interchangeably with "piecewise affine," though strictly speaking, the latter emphasizes the inclusion of the constant term bib_i, providing greater generality over purely homogeneous linear functions (where bi=0b_i = 0). In contexts requiring homogeneity, such as certain geometric or algebraic applications, piecewise linear may refer exclusively to functions without the additive constant. The polyhedral pieces are typically defined by linear inequalities, ensuring the domain decomposition aligns with frameworks. Piecewise linear functions gained prominence in the mid-20th century in and optimization as a tool for approximating nonlinear problems, building on foundational developments in such as George Dantzig's 1947 introduction of the simplex method.

Examples

One prominent example of a piecewise linear function is the absolute value function, defined as f(x)=∣x∣={−xif x<0xif x≥0f(x) = |x| = \begin{cases} -x & \text{if } x < 0 \\ x & \text{if } x \geq 0 \end{cases} Its graph forms a V-shape with the vertex at the origin, consisting of two half-lines: one with slope -1 for negative xx and one with slope 1 for non-negative xx. In machine learning, the rectified linear unit (ReLU) activation function serves as another fundamental piecewise linear example, expressed as f(x)=max⁡(0,x)={0if x<0xif x≥0f(x) = \max(0, x) = \begin{cases} 0 & \text{if } x < 0 \\ x & \text{if } x \geq 0 \end{cases} This function outputs zero for negative inputs and follows the identity line with slope 1 for non-negative inputs, promoting sparsity and efficient computation in neural networks. Piecewise linear functions extend naturally to multiple dimensions; for instance, in two dimensions, a function can be defined over a triangulated domain where it is affine on each triangular region, interpolating linearly via barycentric coordinates from vertex values. Such constructions are common in for approximating surfaces or fields on planar domains. A non-continuous piecewise linear function arises in approximations of , such as the H(x)=0H(x) = 0 for x<0x < 0 and H(x)=1H(x) = 1 for x≥0x \geq 0, which is piecewise constant—hence linear with zero slope—across the discontinuity at x=0x = 0. Smoother approximations might insert a short linear ramp segment over a narrow interval around the jump to model transitions while preserving overall piecewise linearity.

Properties

Continuity and Differentiability

A piecewise linear function, defined as a function that is affine on each subdomain of a partition of its domain, is continuous at a breakpoint cc if the left-hand limit lim⁡x→c−f(x)\lim_{x \to c^-} f(x), the right-hand limit lim⁡x→c+f(x)\lim_{x \to c^+} f(x), and the function value f(c)f(c) are equal. This condition holds when the affine expressions for the adjacent pieces match at cc, ensuring no jump discontinuity occurs. In one dimension, if the pieces are f(x)=Alx+blf(x) = A_l x + b_l for x<cx < c and f(x)=Arx+brf(x) = A_r x + b_r for x≥cx \geq c, continuity requires Alc+bl=Arc+brA_l c + b_l = A_r c + b_r. In higher dimensions, continuity extends to the pieces agreeing on the shared hyperplanes or faces between adjacent polytopes in the domain partition. For adjacent pieces defined by affine functions fP(x)=cP⊤x+dPf_P(x) = c_P^\top x + d_P on polytope PP and fQ(x)=cQ⊤x+dQf_Q(x) = c_Q^\top x + d_Q on polytope QQ, the condition is cP⊤x+dP=cQ⊤x+dQc_P^\top x + d_P = c_Q^\top x + d_Q for all xx in the intersection P∩QP \cap Q, which simplifies to matching values at vertices of the shared face. This ensures the function is well-defined and continuous across boundaries. Piecewise linear functions are differentiable at interior points of each piece, where the derivative equals the constant slope (gradient) of the affine expression for that piece. At breakpoints, differentiability requires the slopes of adjacent pieces to match; if Al=ArA_l = A_r in one dimension (or gradients agree across the boundary hyperplane in higher dimensions), the function is differentiable with derivative AlA_l. Otherwise, the function is not differentiable at the breakpoint due to a corner or kink. The one-sided derivatives always exist and are given by the adjacent slopes: the left derivative f−′(c)=Alf'_-(c) = A_l and the right derivative f+′(c)=Arf'_+(c) = A_r. For convex piecewise linear functions, such as the pointwise maximum of affine functions f(x)=max⁡i(ai⊤x+bi)f(x) = \max_i (a_i^\top x + b_i), the subdifferential at a point xx is the convex hull of the gradients of the active pieces: ∂f(x)=conv{ai∣i∈I(x)}\partial f(x) = \mathrm{conv}\{a_i \mid i \in I(x)\}, where I(x)={i∣ai⊤x+bi=f(x)}I(x) = \{i \mid a_i^\top x + b_i = f(x)\}. At interior points or smooth boundaries where only one piece is active, the subdifferential is a singleton equal to the gradient, indicating differentiability. At kinks where multiple pieces are active, the subdifferential is a polytope with dimension greater than zero, confirming non-differentiability. For example, the absolute value function f(x)=∣x∣f(x) = |x|, which is piecewise linear with pieces f(x)=−xf(x) = -x for x<0x < 0 and f(x)=xf(x) = x for x≥0x \geq 0, is continuous everywhere but not differentiable at x=0x = 0, where ∂f(0)=[−1,1]\partial f(0) = [-1, 1].

Convexity and Other Structural Properties

A piecewise linear function in one dimension is convex if and only if the slopes of its successive linear pieces are non-decreasing, assuming the pieces are ordered according to their domains along the real line. This condition ensures that the function lies below any chord connecting two points on its graph, preserving the defining property of convexity. More generally, in higher dimensions, a piecewise linear function is convex if it can be represented as the pointwise maximum of a finite collection of affine functions, as the maximum of convex functions is itself convex. Monotonicity of a piecewise linear function follows directly from the signs of its slopes. Specifically, the function is non-decreasing over its domain if every slope is non-negative, and it is strictly increasing if every slope is positive. In the context of convex piecewise linear functions, non-decreasing slopes already imply a form of global non-decreasing behavior when combined with non-negative initial slopes, though strict monotonicity requires stricter conditions on the slopes. The boundedness of a piecewise linear function depends on its domain and the slopes of the boundary pieces. On a bounded domain, the function is always bounded above and below, as it is continuous and the domain is compact. On an unbounded domain, such as the entire real line, the function is bounded below if the leftmost slope is non-positive and the rightmost slope is non-negative (or vice versa for bounded above), but it becomes unbounded in the direction where the boundary slope has the same sign as the direction of extension. Piecewise linear functions exhibit Lipschitz continuity when their slopes are bounded. In particular, if the absolute values of all slopes are finite, the function is globally over its domain, with the Lipschitz constant equal to the supremum of the absolute values of the slopes; this follows from the fact that the function's variation is controlled by the steepest linear piece. For convex piecewise linear functions, local holds on open convex sets, but global bounds require uniform control on the slopes.

Approximation Techniques

Fitting to Curves

Piecewise linear functions provide a fundamental approach to approximating smooth nonlinear curves by dividing the domain interval [a,b][a, b] into subintervals and fitting linear segments on each. In uniform piecewise linear interpolation, the interval is partitioned into nn equal subintervals using knots xi=a+ihx_i = a + i h for i=0,1,…,ni = 0, 1, \dots, n, where h=(b−a)/nh = (b - a)/n. The approximation p(x)p(x) is then constructed by connecting the points (xi,f(xi))(x_i, f(x_i)) with straight line segments, ensuring the function passes exactly through these evaluation points. This method is straightforward to implement and computationally efficient, as each segment is defined by the simple linear formula p(x)=f(xi)+f(xi+1)−f(xi)h(x−xi)p(x) = f(x_i) + \frac{f(x_{i+1}) - f(x_i)}{h} (x - x_i) for x∈[xi,xi+1]x \in [x_i, x_{i+1}]. For a twice continuously differentiable function ff, the error in this approximation is bounded by ∣f(x)−p(x)∣≤18h2max⁡t∈[xi,xi+1]∣f′′(t)∣|f(x) - p(x)| \leq \frac{1}{8} h^2 \max_{t \in [x_i, x_{i+1}]} |f''(t)| on each subinterval [xi,xi+1][x_i, x_{i+1}], leading to an overall error of order O(h2max⁡∣f′′∣)O(h^2 \max |f''|). With equidistant knots, this simplifies to ∣f(x)−p(x)∣≤C(b−a)2/n2|f(x) - p(x)| \leq C (b - a)^2 / n^2, where CC depends on the maximum second derivative, demonstrating second-order convergence as the number of subintervals increases. These bounds highlight the method's accuracy for functions with bounded curvature, though the error grows quadratically with subinterval length. To enhance accuracy without uniformly increasing the number of segments, adaptive methods refine the knot placement in regions of high curvature, such as where the second derivative is large. These approaches estimate curvature—often via local quadratic approximations or direct computation of ∣f′′(x)∣|f''(x)|—and insert additional knots to reduce subinterval lengths proportionally to the local variation, ensuring a more equitable error distribution across the domain. For instance, curvature-threshold-based subdivision identifies key points where the curve's bending exceeds a specified tolerance, allowing targeted refinement while maintaining computational efficiency. Piecewise linear interpolation corresponds to a spline of degree 1, characterized by C0C^0 continuity at the knots, meaning the function is continuous but its derivative may exhibit jumps. This structure arises naturally from matching function values at knot points without enforcing derivative continuity, distinguishing it from higher-degree splines. In practice, the construction algorithm begins with knot selection (uniform or adaptive), followed by evaluation of ff at these points, and then determination of linear coefficients on each segment either by direct connection for interpolation or via local least-squares fitting for minor smoothing. Historical roots of these techniques lie in 19th-century graphical methods for astronomical tabulations and engineering drawings, with formal theoretical development in numerical analysis accelerating after the 1950s alongside electronic computing advancements.

Fitting to Data

Fitting piecewise linear functions to discrete, noisy datasets is a common task in statistical modeling, where the goal is to approximate the underlying relationship between variables using segments of linear functions joined at knots, while accounting for observational errors. The standard approach employs least squares estimation to minimize the sum of squared residuals between observed data points and the predicted values from the piecewise linear model. This involves solving an optimization problem where the model parameters—slopes, intercepts, and knot locations—are adjusted to best fit the data, assuming the errors are independent and identically distributed. For a dataset {(xi,yi)}i=1n\{(x_i, y_i)\}_{i=1}^n, the objective is to minimize ∑i=1n(yi−f(xi))2,\sum_{i=1}^n (y_i - f(x_i))^2, where ff is a continuous piecewise linear function with kk breaks (knots) at positions τ1<τ2<⋯<τk\tau_1 < \tau_2 < \dots < \tau_k, such that f(x)=βj0+βj1xf(x) = \beta_{j0} + \beta_{j1} x for xx in the jj-th interval defined by the knots. When knots are fixed in advance, the problem reduces to separate linear regressions on each segment, with continuity constraints enforced at the joins to ensure smoothness. For variable knots, optimization algorithms such as differential evolution or dynamic programming are used to simultaneously estimate knot positions and segment parameters, as the objective function is non-convex but can leverage the piecewise linearity for efficient computation. Knot selection is crucial for balancing model complexity and fit, often guided by information criteria like the Akaike Information Criterion (AIC) or Bayesian Information Criterion (BIC), which penalize additional pieces to avoid overfitting. These criteria evaluate models with varying numbers of knots, selecting the one that minimizes AIC = -2 log(L) + 2p or BIC = -2 log(L) + p log(n), where L is the likelihood and p the number of parameters. Alternative methods include forward selection, starting with a single line and iteratively adding knots where they most reduce residuals, or backward selection from an overparameterized model. Change-point detection methods identify potential knots by testing for structural breaks in the data, such as abrupt shifts in slope. Statistical tests like the cumulative sum (CUSUM) procedure monitor the partial sums of residuals or score statistics to detect deviations from a null linear model, signaling a change point when the CUSUM statistic exceeds a threshold derived from asymptotic distributions or simulations. For multiple change points, sequential testing or penalized likelihood approaches extend this framework. Implementations are available in statistical software; for example, the R package 'segmented' fits piecewise linear models via iterative least squares, estimating breakpoints and supporting AIC/BIC for selection. In Python, the 'pwlf' library uses differential evolution to optimize continuous piecewise linear fits for a specified number of segments. A basic pseudocode for segmented regression with fixed knots might proceed as follows:

Initialize parameters: slopes and intercepts for each segment While convergence not achieved: For each segment j: Fit linear regression to data points in interval j, using continuity at knots Update knot positions if variable (e.g., via grid search or optimization) Compute residuals and check change in objective < tolerance Return fitted parameters and function

Initialize parameters: slopes and intercepts for each segment While convergence not achieved: For each segment j: Fit linear regression to data points in interval j, using continuity at knots Update knot positions if variable (e.g., via grid search or optimization) Compute residuals and check change in objective < tolerance Return fitted parameters and function

This iterative process ensures continuity and minimizes the least squares objective. Noisy data is typically handled under the assumption of Gaussian errors in the least squares framework, leading to maximum likelihood estimates equivalent to the minimizer of the squared residual sum. For robustness against outliers, the objective can integrate Huber loss, which combines quadratic behavior for small residuals (∣r∣≤δ|r| \leq \delta) with linear penalties for large ones (∣r∣>δ|r| > \delta), defined as ρ(r)=r2/2\rho(r) = r^2/2 if ∣r∣≤δ|r| \leq \delta, else δ(∣r∣−δ/2)\delta(|r| - \delta/2). This approach reduces sensitivity to heavy-tailed errors while maintaining efficiency for .

Extensions

Generalizations

Piecewise linear functions generalize to multivariate settings by extending the domain to Rn\mathbb{R}^n and partitioning it into polyhedral regions defined by intersections of hyperplanes, ensuring compatibility across boundaries to maintain function properties such as continuity where desired. On each polyhedron PiP_i in this partition, the function takes the affine form f(x)=aiTx+bif(x) = a_i^T x + b_i, where ai∈Rna_i \in \mathbb{R}^n and bi∈Rb_i \in \mathbb{R}, allowing representation of complex behaviors through linear pieces in higher dimensions. Such multivariate piecewise linear functions are particularly useful in constructing piecewise linear homeomorphisms, which are bijective mappings that preserve topological structure and are affine on each polyhedral cell, facilitating approximations of invertible transformations in geometric and optimization contexts. In settings with potentially infinite pieces, continuous piecewise linear (CPL) functions emerge as limits of finite piecewise linear approximations, where linearity holds on intervals or polyhedra separated by countably many breakpoints, while ensuring overall continuity. A key theoretical foundation is the density of piecewise linear functions in the space of on compact sets, such as C[0,1]C[0,1] under the ; this follows from a Stone-Weierstrass-type , where piecewise linears form an algebra that separates points and approximates any continuous function arbitrarily closely. This density extends to multivariate cases on compact subsets of Rn\mathbb{R}^n, underscoring the expressive power of piecewise linear structures for universal approximation. Piecewise linear functions integrate deeply with nonsmooth analysis, particularly in handling variational inequalities, where the function's linear pieces on polyhedral domains allow second-order variational analysis to characterize stability and regularity without relying on differentiability. For instance, generalized derivatives of these functions enable the formulation and solution of variational inequalities over nonsmooth sets, providing tools for parametric stability in optimization problems. Recent advances in the 2020s have leveraged to construct high-dimensional piecewise linear approximations, notably through ReLU neural networks, which inherently define multivariate piecewise linear functions via partitions induced by activation thresholds, achieving efficient universal rates for smooth functions in Rn\mathbb{R}^n. More recent developments include trainable piecewise-linear spline activations for improved performance in image classification and physics modeling as of 2025, and the TeLU for faster and more stable training in 2024. These networks exploit the piecewise linear nature to scale to high dimensions, offering improved over traditional methods for tasks requiring fine-grained approximations on complex domains.

Specializations

Continuous piecewise linear functions, often abbreviated as CPL functions, impose the additional constraint of continuity at all breakpoints on the general piecewise linear form. This ensures that the function value matches from both sides at each , resulting in a smooth connection between adjacent linear segments without jumps. The set of all such functions over a fixed interval with specified breakpoints forms a , as linear combinations and scalar multiples preserve both the piecewise linearity and continuity properties. For CPL functions defined on a closed interval [a,b][a, b] with kk interior knots, the dimension of this is k+2k + 2. This dimension arises because the is equivalent to specifying independent values at the k+2k + 2 knots (including the endpoints), with the function linearly interpolating between them. Convex piecewise linear functions represent a further restricted subclass where the overall function is convex, typically achieved by ensuring that the slopes of successive linear segments are nondecreasing across the ordered breakpoints. This ordering of slopes guarantees that the function lies above its tangents and satisfies the convexity inequality f(λx+(1−λ)y)≤λf(x)+(1−λ)f(y)f(\lambda x + (1-\lambda) y) \leq \lambda f(x) + (1-\lambda) f(y) for λ∈[0,1]\lambda \in [0,1]. Such functions are particularly useful in optimization contexts due to their compatibility with tools. A key representation of convex piecewise linear functions is as the pointwise maximum of a finite collection of affine functions, i.e., f(x)=max⁡i(aiTx+bi)f(x) = \max_i (a_i^T x + b_i), where the epigraph {(x,t)∣t≥f(x)}\{(x, t) \mid t \geq f(x)\} forms a convex polyhedral set. This max-affine form highlights the convexity, as the maximum of convex (affine) functions is convex, and the epigraph's polyhedral structure facilitates computational handling. Linear splines constitute a specialization of piecewise linear functions with fixed knot locations, where the function is linear between knots and continuous overall. These form the foundational basis for constructing higher-degree splines, such as cubic splines, through recursive integration or differentiation while maintaining the knot structure. The fixed knots ensure a stable partition of the domain, enabling systematic basis expansion for approximation purposes. Tropical piecewise linear functions arise in the context of max-plus algebra, a structure where addition is replaced by maximization and multiplication by standard addition. In this framework, a tropical piecewise linear function takes the form f(x)=max⁡i(Aix+bi)f(x) = \max_i (A_i x + b_i), representing the tropical analog of classical polynomials and inheriting piecewise linearity from the dominating linear terms in different regions. These functions are inherently convex and play a role in for modeling piecewise linear surfaces. Multivariate extensions of these specializations exist, adapting the continuity, convexity, or tropical structures to higher dimensions while preserving core properties.

Applications

In Optimization

Piecewise linear functions are essential in optimization for modeling nonsmooth objectives and constraints that arise in applications such as and network flows. A convex piecewise linear function can be represented as the pointwise maximum of a finite collection of affine functions, which facilitates its reformulation into an equivalent through the introduction of epigraph variables. This approach transforms nonsmooth minimization problems into tractable linear constraints, preserving the problem's structure while enabling standard solvers. Consider minimizing f(x)f(x) where ff is a convex piecewise linear function defined over pieces with affine expressions aiTx+bia_i^T x + b_i for i=1,…,mi = 1, \dots, m. This is equivalent to the linear program min⁡ts.t.t≥aiTx+bi,i=1,…,mx∈Rn, t∈R.\begin{align*} \min &\quad t \\ \text{s.t.} &\quad t \geq a_i^T x + b_i, \quad i = 1, \dots, m \\ &\quad x \in \mathbb{R}^n, \ t \in \mathbb{R}. \end{align*} The epigraph variable tt upper-bounds the function value, ensuring the objective captures the maximum over the linear pieces. To incorporate piecewise linear constraints directly into linear programming frameworks, special ordered sets of type 2 (SOS2) are utilized, which enforce that at most two adjacent variables in an ordered set are nonzero, modeling convex combinations within a single piece efficiently without auxiliary integer variables. This technique integrates seamlessly with the , avoiding the need for explicit mixed-integer formulations in convex cases. For nonconvex piecewise linear functions, where the objective or constraints may exhibit local minima or discontinuities, mixed-integer programming formulations employ binary variables to select the active piece among the candidates. A representative approach is the disaggregated convex combination formulation, which uses binary variables yP∈{0,1}y_P \in \{0,1\} to indicate the selected piece PP and nonnegative continuous variables λP,v\lambda_{P,v} to form a convex combination of breakpoints vv within that piece, subject to ∑PyP=1\sum_{P} y_P = 1 and ∑v∈V(P)λP,v=yP\sum_{v \in V(P)} \lambda_{P,v} = y_P. This ensures global optimality by enumerating piece selections through integer constraints. Efficient algorithms exploit the structure of these formulations: for convex piecewise linear problems, the convex simplex method extends the classical simplex algorithm to handle separable convex objectives under linear constraints, pivoting along piecewise linear rays to achieve finite convergence. In nonconvex settings, branch-and-bound or branch-and-cut procedures partition the domain based on SOS2 constraints or piece selections, generating valid inequalities such as lifted cover cuts to strengthen relaxations and prune suboptimal branches without mandatory binary variables for separable functions. The use of piecewise linear functions in optimization traces back to operations research in the 1960s, when E. M. L. Beale developed early mixed-integer programming codes incorporating branch-and-bound for nonsmooth problems, enabling practical solutions to industrial applications like planning. Beale and Tomlin's introduction of SOS2 in 1970 further solidified their role by providing a specialized mechanism for nonconvex piecewise linear modeling within general mathematical programming systems.

In Computer Graphics and Modeling

In , piecewise linear functions serve as a foundational tool for approximating complex curves and surfaces, enabling efficient rendering, manipulation, and interaction in visual modeling. By representing smooth geometries as sequences of straight line segments, these functions facilitate rasterization and on GPUs, balancing computational cost with visual fidelity. This approach is particularly valuable in scenarios requiring real-time performance, such as and . One key application is the polygonization of curves, where smooth paths are approximated by polygonal chains composed of connected linear segments. This process reduces continuous curves to discrete piecewise linear representations suitable for display and processing. For example, algorithms optimize segment placement based on chord properties to achieve accurate approximations of space curves while minimizing the number of vertices. Similarly, Bézier curves are linearized through subdivision into linear segments for rasterization; each cubic or quadratic Bézier segment is iteratively split and triangulated within its , allowing GPU-based rendering of vector art without excessive computational overhead. The parametric form of a piecewise linear underscores its simplicity and utility in pipelines. For a segment connecting points Pi=(xi,yi)P_i = (x_i, y_i) and Pi+1=(xi+1,yi+1)P_{i+1} = (x_{i+1}, y_{i+1}) over t∈[0,1]t \in [0, 1], x(t)=xi+t(xi+1−xi),y(t)=yi+t(yi+1−yi).\begin{align*} x(t) &= x_i + t (x_{i+1} - x_i), \\ y(t) &= y_i + t (y_{i+1} - y_i). \end{align*} This , often denoted as lerp, ensures C0C^0 continuity at junctions and directly supports transformations like and scaling. In , triangular meshes represent surfaces as piecewise linear approximations over simplicial complexes, where each forms a planar facet connecting three vertices. This structure approximates curved manifolds with connected, non-overlapping , enabling of attributes like normals and textures via barycentric coordinates for smooth shading. Such meshes are ubiquitous in rendering pipelines, supporting applications from to finite element analysis. Piecewise linear boundaries also enhance by defining object geometries as polygonal or planar patches, allowing efficient intersection tests between elements like edges and faces. In composite models, linear segments reduce 3D collision queries to lower-dimensional problems, such as line-quadric or line-line intersections, solved via root-finding for contact times. This enables robust, continuous detection in dynamic scenes without full curve evaluations. Modern implementations leverage these principles in CAD software and games. In tools like , polylines embody piecewise linear paths as single objects comprising sequential line segments, supporting precise drafting and editing of complex outlines. In gaming, within shaders—performed automatically by the GPU rasterizer—blends vertex attributes across , optimizing real-time effects like color gradients and deformations on post-2010 hardware with unified shader architectures.

References

  1. https://mathresearch.utsa.edu/wiki/index.php?title=Piecewise_Linear_Function
  2. https://ise.ncsu.edu/wp-content/uploads/sites/9/2020/08/789-Lecture-2.pdf
  3. https://online.stat.psu.edu/stat501/lesson/8/8.8
  4. https://www.isye.gatech.edu/~sahmed/PWL_LI_09.pdf
  5. https://www.ie.uh.edu/news/department-news/202009/piecewise-linear-optimization-machine-learning
  6. https://dspace.mit.edu/bitstream/handle/1721.1/4767/RLE-TR-315-04734641.pdf?sequence=1
  7. https://link.springer.com/chapter/10.1007/978-3-540-72701-9_4
  8. https://www.tandfonline.com/doi/abs/10.1080/02331939408844018
  9. https://www.sciencedirect.com/science/article/abs/pii/S0005109807004906
  10. https://mathoverflow.net/questions/437027/fixed-points-of-rational-continuous-piecewise-affine-maps
  11. https://see.stanford.edu/materials/lsocoee364a/01introduction.pdf
  12. https://mathworld.wolfram.com/PiecewiseFunction.html
  13. https://www.cs.toronto.edu/~fritz/absps/reluICML.pdf
  14. https://courses.cs.duke.edu/fall06/cps296.1/Lectures/sec-V-3.pdf
  15. https://tutorial.math.lamar.edu/classes/de/StepFunctions.aspx
  16. https://www2.isye.gatech.edu/~atoriello3/pwl_fit_models.pdf
  17. http://www.seas.ucla.edu/~vandenbe/236C/lectures/subgradients.pdf
  18. https://ampl.com/wp-content/uploads/Chapter-17-Piecewise-Linear-Programs-AMPL-Book.pdf
  19. https://see.stanford.edu/materials/lsocoee364a/03convexfunctions.pdf
  20. https://math.washington.edu/~burke/crs/cvx15/notes/RoW_convexity.pdf
  21. https://engcourses-uofa.ca/introduction-to-numerical-analysis/piecewise-interpolation/
  22. https://tobydriscoll.net/fnc-julia/localapprox/pwlin.html
  23. https://math.umd.edu/~petersd/460/spline_n.pdf
  24. https://www.nature.com/articles/s41598-022-20018-9
  25. https://web.cs.ucdavis.edu/~hamann/HamannChen1994a.pdf
  26. https://bigwww.epfl.ch/publications/meijering0201.pdf
  27. https://www.sciencedirect.com/science/article/pii/S0898122100003370
  28. https://www.researchgate.net/publication/331231072_pwlf_A_Python_Library_for_Fitting_1D_Continuous_Piecewise_Linear_Functions
  29. https://jerryzli.github.io/talks/piecewise.pdf
  30. https://pmc.ncbi.nlm.nih.gov/articles/PMC4297674/
  31. https://journal.r-project.org/articles/RN-2008-004/RN-2008-004.pdf
  32. https://www.sciencedirect.com/science/article/abs/pii/S0167947306005184
  33. https://arxiv.org/html/2503.05270v1
  34. https://yoksis.bilkent.edu.tr/pdf/files/10.1016-S0893-9659%2897%2900061-X.pdf
  35. https://www.itk.ntnu.no/_media/emner/fordypning/l14-pwl-multidimensional.pdf
  36. https://www.sciencedirect.com/science/article/pii/S0377042711002913
  37. https://link.springer.com/chapter/10.1007/978-1-4612-9906-6_6
  38. https://ieeexplore.ieee.org/document/5530927/
  39. https://dl.acm.org/doi/10.1007/s10957-016-0897-y
  40. https://www.sciencedirect.com/science/article/abs/pii/S0362546X15003843
  41. https://arxiv.org/pdf/2007.08729
  42. https://arxiv.org/abs/2509.18161
  43. https://arxiv.org/abs/2412.20269
  44. https://direct.mit.edu/neco/article/32/11/2249/95633/ReLU-Networks-Are-Universal-Approximators-via
  45. https://math.iisc.ac.in/~patil/web_courses/lalg03/la03-e04.pdf
  46. https://web.stanford.edu/class/ee364a/lectures/functions.pdf
  47. https://personal.math.vt.edu/embree/math5466/lecture10.pdf
  48. https://bookdown.org/ssjackson300/Machine-Learning-Lecture-Notes/splines.html
  49. https://arxiv.org/abs/1912.03891
  50. https://manosth.github.io/files/papers/MaragosTheodosis_TropicalPiecewiseLinearRegression_ICASSP20.pdf
  51. https://www.sciencedirect.com/science/article/pii/S1063520323000684
  52. https://www.seas.ucla.edu/~vandenbe/ee236a/lectures/pwl.pdf
  53. https://www.informs.org/Explore/History-of-O.R.-Excellence/O.R.-Methodologies/Optimization-Mathematical-Programming
  54. https://juan-pablo-vielma.github.io/publications/Mixed-Integer-Models-for-Nonseparable.pdf
  55. https://pubsonline.informs.org/doi/10.1287/mnsc.14.3.221
  56. https://pubsonline.informs.org/doi/10.1287/opre.1060.0277
  57. https://webdiis.unizar.es/~jcampos/ab/restringido/A%20brief%20history%20of%20LP%20and%20MIP.pdf
  58. https://raphlinus.github.io/graphics/curves/2019/12/23/flatten-quadbez.html
  59. http://www.cs.umd.edu/~reastman/slides/CMSC427PiecewiseParametricNotes.pdf
  60. https://www.cs.cornell.edu/courses/cs4620/2020fa/slides/09trimesh.pdf
  61. https://i.cs.hku.hk/~ykchoi/quadrics/cqm.pdf
  62. https://help.autodesk.com/view/ACD/2024/ENU/?guid=GUID-392BF13C-D9E7-47A8-8E07-435296332279
  63. https://developer.arm.com/documentation/100140/latest/advanced-graphics-techniques/custom-shaders/vertex-shader-output-and-varyings
Add your contribution
Related Hubs
Contribute something
User Avatar
No comments yet.