Turbo code

The fundamental patent application for turbo codes was filed on 23 April 1991. The patent application lists Claude Berrou as the sole inventor of turbo codes. The patent filing resulted in several patents including US Patent 5,446,747, which expired 29 August 2013.

The first public paper on turbo codes was "Near Shannon Limit Error-correcting Coding and Decoding: Turbo-codes".^[4] This paper was published 1993 in the Proceedings of IEEE International Communications Conference. The 1993 paper was formed from three separate submissions that were combined due to space constraints. The merger caused the paper to list three authors: Berrou, Glavieux, and Thitimajshima (from Télécom Bretagne, former ENST Bretagne, France). However, it is clear from the original patent filing that Berrou is the sole inventor of turbo codes and that the other authors of the paper contributed material other than the core concepts.^{[improper synthesis]}

Turbo codes were so revolutionary at the time of their introduction that many experts in the field of coding did not believe the reported results. When the performance was confirmed a small revolution in the world of coding took place that led to the investigation of many other types of iterative signal processing.^[5]

The first class of turbo code was the parallel concatenated convolutional code (PCCC). Since the introduction of the original parallel turbo codes in 1993, many other classes of turbo code have been discovered, including serial concatenated convolutional codes and repeat-accumulate codes. Iterative turbo decoding methods have also been applied to more conventional FEC systems, including Reed–Solomon corrected convolutional codes, although these systems are too complex for practical implementations of iterative decoders. Turbo equalization also flowed from the concept of turbo coding.

In addition to turbo codes, Berrou also invented recursive systematic convolutional (RSC) codes, which are used in the example implementation of turbo codes described in the patent. Turbo codes that use RSC codes seem to perform better than turbo codes that do not use RSC codes.

Prior to turbo codes, the best constructions were serial concatenated codes based on an outer Reed–Solomon error correction code combined with an inner Viterbi-decoded short constraint length convolutional code, also known as RSV codes.

In a later paper, Berrou gave credit to the intuition of "G. Battail, J. Hagenauer and P. Hoeher, who, in the late 80s, highlighted the interest of probabilistic processing." He adds "R. Gallager and M. Tanner had already imagined coding and decoding techniques whose general principles are closely related," although the necessary calculations were impractical at that time.^[6]

There are many different instances of turbo codes, using different component encoders, input/output ratios, interleavers, and puncturing patterns. This example encoder implementation describes a classic turbo encoder, and demonstrates the general design of parallel turbo codes.

This encoder implementation sends three sub-blocks of bits. The first sub-block is the m-bit block of payload data. The second sub-block is n/2 parity bits for the payload data, computed using a recursive systematic convolutional code (RSC code). The third sub-block is n/2 parity bits for a known permutation of the payload data, again computed using an RSC code. Thus, two redundant but different sub-blocks of parity bits are sent with the payload. The complete block has m + n bits of data with a code rate of m/(m + n). The permutation of the payload data is carried out by a device called an interleaver.

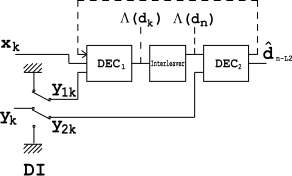
Hardware-wise, this turbo code encoder consists of two identical RSC coders, C₁ and C₂, as depicted in the figure, which are connected to each other using a concatenation scheme, called parallel concatenation:

In the figure, M is a memory register. The delay line and interleaver force input bits d_k to appear in different sequences. At first iteration, the input sequence d_k appears at both outputs of the encoder, x_k and y_1k or y_2k due to the encoder's systematic nature. If the encoders C₁ and C₂ are used in n₁ and n₂ iterations, their rates are respectively equal to

${\displaystyle {\begin{aligned}~R_{1}&={\frac {n_{1}+n_{2}}{2n_{1}+n_{2}}}\\~R_{2}&={\frac {n_{1}+n_{2}}{n_{1}+2n_{2}}}\end{aligned}}}$

The decoder is built in a similar way to the above encoder. Two elementary decoders are interconnected to each other, but in series, not in parallel. The ${\displaystyle \textstyle DEC_{1}}$ decoder operates on lower speed (i.e., ${\displaystyle \textstyle R_{1}}$), thus, it is intended for the ${\displaystyle \textstyle C_{1}}$ encoder, and ${\displaystyle \textstyle DEC_{2}}$ is for ${\displaystyle \textstyle C_{2}}$ correspondingly. ${\displaystyle \textstyle DEC_{1}}$ yields a soft decision which causes ${\displaystyle \textstyle L_{1}}$ delay. The same delay is caused by the delay line in the encoder. The ${\displaystyle \textstyle DEC_{2}}$'s operation causes ${\displaystyle \textstyle L_{2}}$ delay.

An interleaver installed between the two decoders is used here to scatter error bursts coming from ${\displaystyle \textstyle DEC_{1}}$ output. DI block is a demultiplexing and insertion module. It works as a switch, redirecting input bits to ${\displaystyle \textstyle DEC_{1}}$ at one moment and to ${\displaystyle \textstyle DEC_{2}}$ at another. In OFF state, it feeds both ${\displaystyle \textstyle y_{1k}}$ and ${\displaystyle \textstyle y_{2k}}$ inputs with padding bits (zeros).

Consider a memoryless AWGN channel, and assume that at k-th iteration, the decoder receives a pair of random variables:

${\displaystyle {\begin{aligned}~x_{k}&=(2d_{k}-1)+a_{k}\\~y_{k}&=2(Y_{k}-1)+b_{k}\end{aligned}}}$

where ${\displaystyle \textstyle a_{k}}$ and ${\displaystyle \textstyle b_{k}}$ are independent noise components having the same variance ${\displaystyle \textstyle \sigma ^{2}}$. ${\displaystyle \textstyle Y_{k}}$ is a k-th bit from ${\displaystyle \textstyle y_{k}}$ encoder output.

Redundant information is demultiplexed and sent through DI to ${\displaystyle \textstyle DEC_{1}}$ (when ${\displaystyle \textstyle y_{k}=y_{1k}}$) and to ${\displaystyle \textstyle DEC_{2}}$ (when ${\displaystyle \textstyle y_{k}=y_{2k}}$).

${\displaystyle \textstyle DEC_{1}}$ yields a soft decision; i.e.:

${\displaystyle \Lambda (d_{k})=\log {\frac {p(d_{k}=1)}{p(d_{k}=0)}}}$

and delivers it to ${\displaystyle \textstyle DEC_{2}}$. ${\displaystyle \textstyle \Lambda (d_{k})}$ is called the logarithm of the likelihood ratio (LLR). ${\displaystyle \textstyle p(d_{k}=i),\,i\in \{0,1\}}$ is the a posteriori probability (APP) of the ${\displaystyle \textstyle d_{k}}$ data bit which shows the probability of interpreting a received ${\displaystyle \textstyle d_{k}}$ bit as ${\displaystyle \textstyle i}$. Taking the LLR into account, ${\displaystyle \textstyle DEC_{2}}$ yields a hard decision; i.e., a decoded bit.

It is known that the Viterbi algorithm is unable to calculate APP, thus it cannot be used in ${\displaystyle \textstyle DEC_{1}}$. Instead of that, a modified BCJR algorithm is used. For ${\displaystyle \textstyle DEC_{2}}$, the Viterbi algorithm is an appropriate one.

However, the depicted structure is not an optimal one, because ${\displaystyle \textstyle DEC_{1}}$ uses only a proper fraction of the available redundant information. In order to improve the structure, a feedback loop is used (see the dotted line on the figure).

The decoder front-end produces an integer for each bit in the data stream. This integer is a measure of how likely it is that the bit is a 0 or 1 and is also called soft bit. The integer could be drawn from the range [−127, 127], where:

• −127 means "certainly 0"
• −100 means "very likely 0"
• 0 means "it could be either 0 or 1"
• 100 means "very likely 1"
• 127 means "certainly 1"

This introduces a probabilistic aspect to the data-stream from the front end, but it conveys more information about each bit than just 0 or 1.

For example, for each bit, the front end of a traditional wireless-receiver has to decide if an internal analog voltage is above or below a given threshold voltage level. For a turbo code decoder, the front end would provide an integer measure of how far the internal voltage is from the given threshold.

To decode the m + n-bit block of data, the decoder front-end creates a block of likelihood measures, with one likelihood measure for each bit in the data stream. There are two parallel decoders, one for each of the n⁄2-bit parity sub-blocks. Both decoders use the sub-block of m likelihoods for the payload data. The decoder working on the second parity sub-block knows the permutation that the coder used for this sub-block.

The key innovation of turbo codes is how they use the likelihood data to reconcile differences between the two decoders. Each of the two convolutional decoders generates a hypothesis (with derived likelihoods) for the pattern of m bits in the payload sub-block. The hypothesis bit-patterns are compared, and if they differ, the decoders exchange the derived likelihoods they have for each bit in the hypotheses. Each decoder incorporates the derived likelihood estimates from the other decoder to generate a new hypothesis for the bits in the payload. Then they compare these new hypotheses. This iterative process continues until the two decoders come up with the same hypothesis for the m-bit pattern of the payload, typically in 15 to 18 cycles.

An analogy can be drawn between this process and that of solving cross-reference puzzles like crossword or sudoku. Consider a partially completed, possibly garbled crossword puzzle. Two puzzle solvers (decoders) are trying to solve it: one possessing only the "down" clues (parity bits), and the other possessing only the "across" clues. To start, both solvers guess the answers (hypotheses) to their own clues, noting down how confident they are in each letter (payload bit). Then, they compare notes, by exchanging answers and confidence ratings with each other, noticing where and how they differ. Based on this new knowledge, they both come up with updated answers and confidence ratings, repeating the whole process until they converge to the same solution.

Turbo codes perform well due to the attractive combination of the code's random appearance on the channel together with the physically realisable decoding structure. Turbo codes are affected by an error floor.

Telecommunications:

• Turbo codes are used extensively in 3G and 4G mobile telephony standards; e.g., in HSPA, EV-DO and LTE.
• MediaFLO, terrestrial mobile television system from Qualcomm.
• The interaction channel of satellite communication systems, such as DVB-RCS^[7] and DVB-RCS2.
• Recent NASA missions such as Mars Reconnaissance Orbiter use turbo codes as an alternative to Reed–Solomon error correction-Viterbi decoder codes.
• IEEE 802.16 (WiMAX), a wireless metropolitan network standard, uses block turbo coding and convolutional turbo coding.

From an artificial intelligence viewpoint, turbo codes can be considered as an instance of loopy belief propagation in Bayesian networks.^[8]

• BCJR algorithm
• Convolutional code
• Forward error correction
• Interleaver
• Low-density parity-check code
• Serial concatenated convolutional codes
• Soft-decision decoding
• Turbo equalizer
• Viterbi algorithm